巧用对称变换突破最短路径
2021-06-05庄宇
庄宇

最值问题分代数最值和几何最值两类,其中几何最值问题既能考查同学们对知识的灵活运用能力,又能更好地体现试题的区分度和效度,是近几年数学学科中考命题者偏爱的压轴题型之一. 下面举例介绍此类问题的破解之法,希望能对同学们有所帮助.
[ 原题再现]
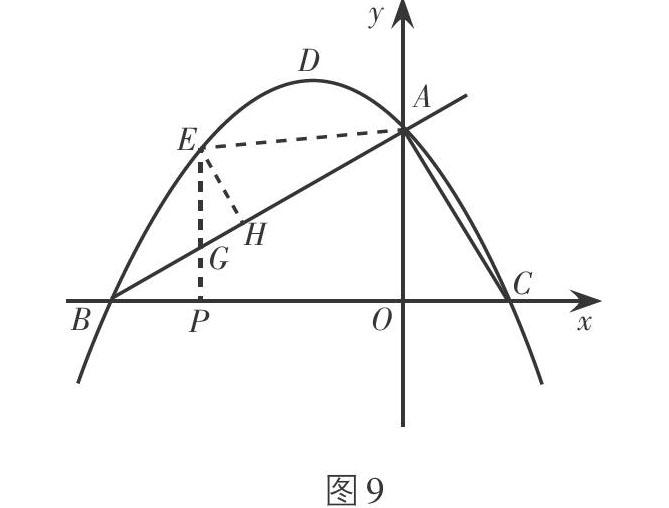
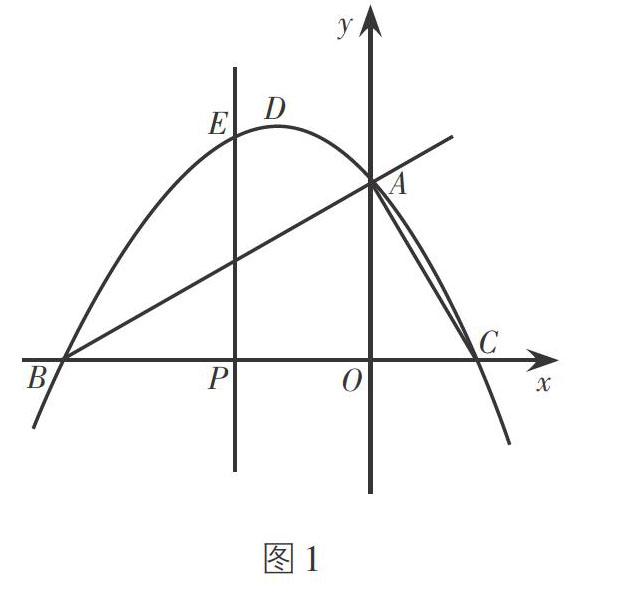
例(2015·辽宁·沈阳·第25题)如图1,在平面直角坐标系中,抛物线[y=-23x2-43x+2]与x轴交于B,C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.
①过点P作x轴的垂线交抛物线于点E,若PE = PC,求点E的坐标;
②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;
③若点Q是线段AB上的动点(点Q不与点A,B重合),点R是线段AC上的动点(点R不与点A,C重合),请直接写出△PQR周长的最小值.
[ 破解策略]
(1)第一问属于典型的代数计算,此问题的设置符合数学课程标准对二次函数知识的基本要求,使试题变得容易入手,同时也为解决后面的问题做好了铺垫.
(2)第二问可根据抛物线的解析式设出点E的坐标,利用转化的思想,把点的坐标转化成线段长,再根据PE = PC建立一个一元二次方程的数学模型,解出方程即可求出点E的坐标.这个求解过程中包括了点的坐标与线段的转化,以及通过等量关系建立方程求线段长等常用的方法,这是同学们必须要掌握的.
(3)第三问中由“点F到EA和ED的距离相等”和角平分线性质定理的逆定理可知EF是∠AED的平分线. 如何确定点F在坐标轴上的位置,进而求出EF的长,是此问的第一个难点.图1中点A,E,D的坐标隐含了角平分线EF与坐标轴的特殊位置关系,这个位置关系可以通过三角函数解决. 这里很多同学容易忽视另外一个问题,就是本题的图形中角平分线EF没有明确画出,究其原因就是其位置不确定,这就需要同学们结合题意考虑图形的各种可能性,进行分类讨论,这是此问的第二个难点.
(4)第四问具有一定的思维难度,此类问题通常的思考角度有两个:
①三角形周长最短,也就是线段和最短,最容易联想到的知识是“将军饮马”问题,因此解题策略就是利用轴对称知识实现“折”变“直”.
②问题表面上是“三个动点”,让人感觉有些束手无策,但是通常可以把其中一点固定住,变成两个动点问题 (把x轴上的点P固定),此时试题就演变成我们常见的下面这道问题:
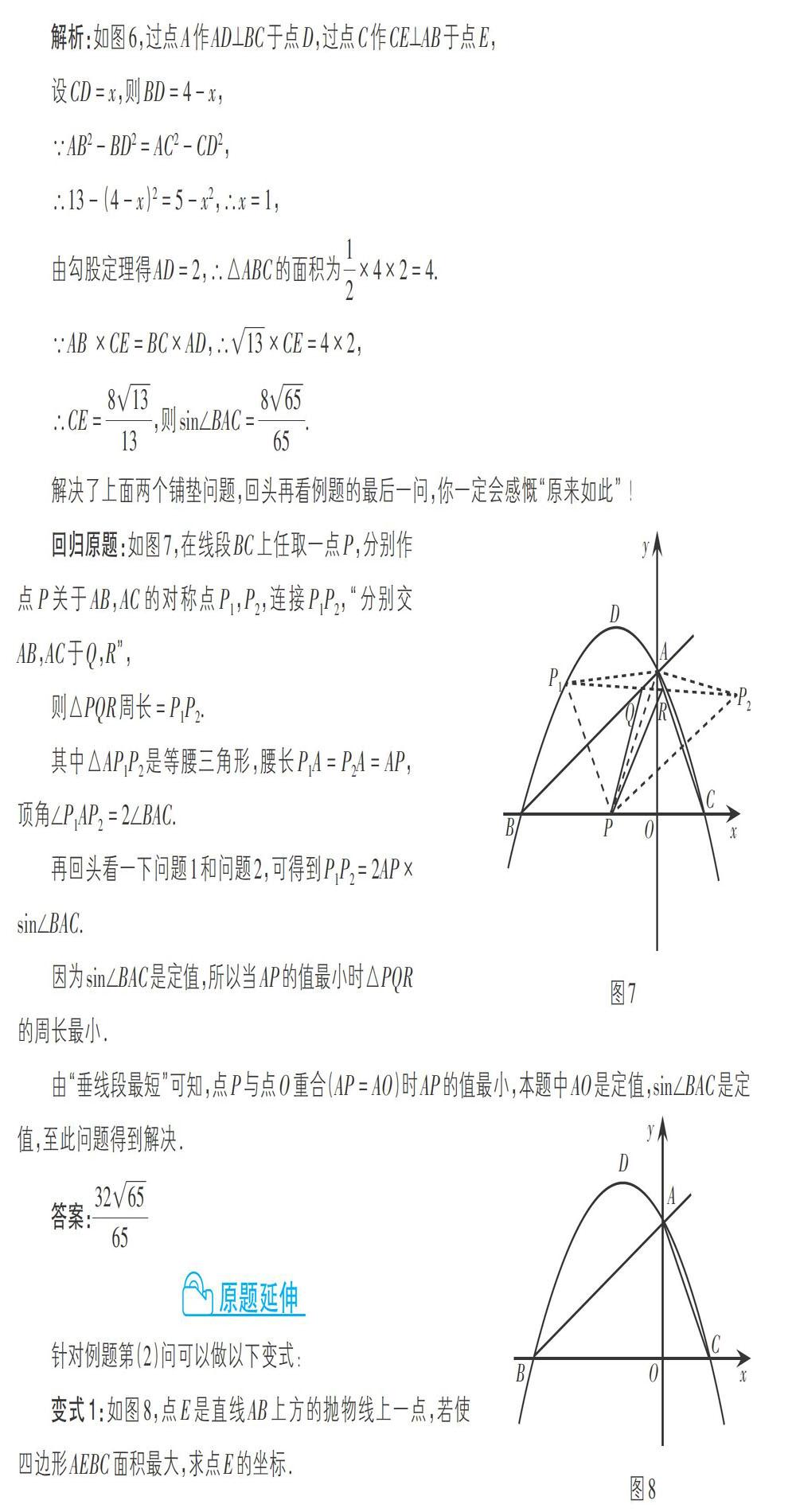
问题1:如图2,点P是∠MON内任意一点,∠MON = α°,OP = a,在射线OM,ON上各找一点A,B,使△PAB的周长最短,并求出△PAB的周长的最小值.(此题后面给出答案)
这样就把一个陌生的试题演变成我们常见的问题进行解决.
任何一道“难题”都是在由若干个基本知识作铺垫的基础上产生的,而思路受阻的原因之一往往是忽略那些由已知条件能直接得到的结论,因此良好的“标图”习惯可以帮助我们直观地获得结论,进而突破难点.
此问中就需要掌握“已知三角形的三边求其高”“等腰三角形的三线合一性质”“三角函数”等初中阶段较为重要的数学基础知识.所以我们可以通过“标图”后进行如下思考:
由本题的第(1)问已经求出A,B,C,D四个点的坐标,进而可求AB,BC,AC的长,至此还能得到什么结果?△ABC的面积是多少?△ABC三边上的高是多少?△ABC三个锐角的三角函数值是多少?……
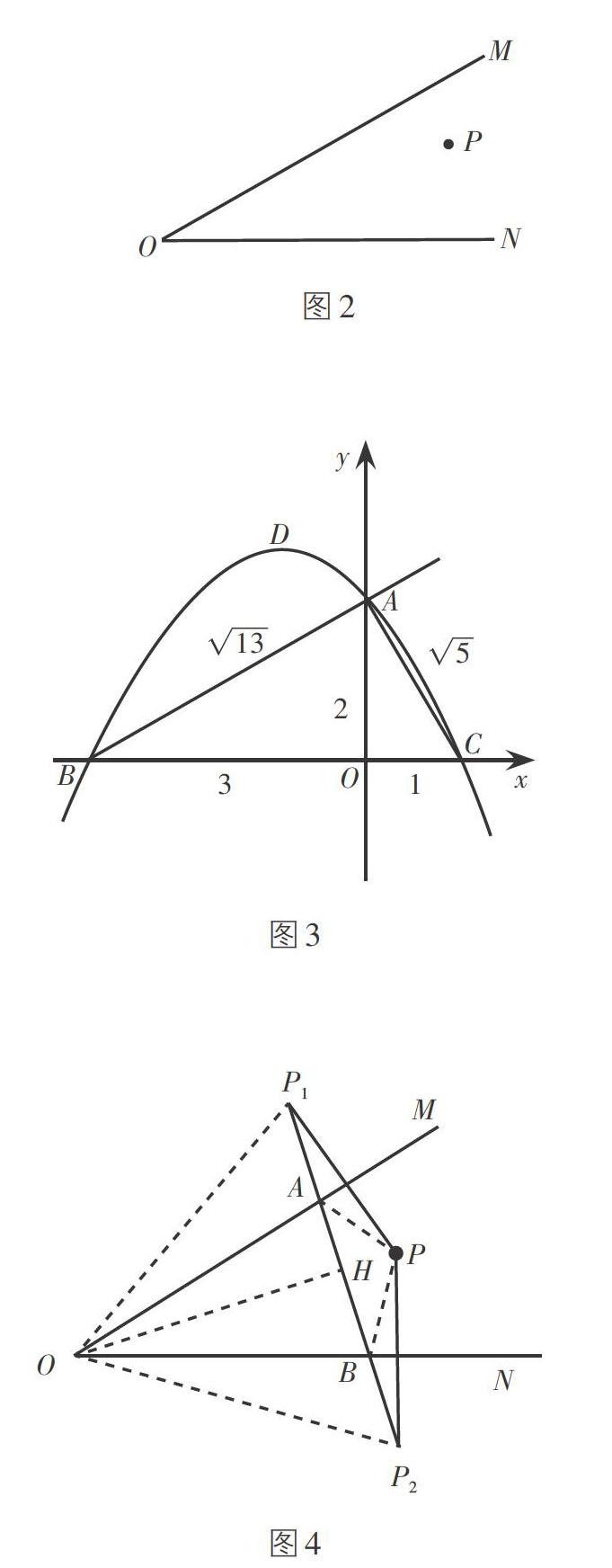
如图3所示,△ABC的三边长易求,利用面积法可求出三边上的高,这样三个锐角的三角函数值就容易求出了.
注:若我们平时有这种“追问”的习惯,相信很多难题都会被我们脱下“伪装”的外衣!
让我们来解决问题1.
解析:这是“将军饮马”问题的基本模型.
如图4,分别作点P关于OM,ON的对称点P1,P2,连接P1P2,分别交OM,ON于点A,B,则△PAB的周长 = P1P2,
连接OP1,OP2,
则可得△OP1P2是等腰三角形,且腰长为a,顶角为2α°,
过点O作OH⊥P1P2于H,利用“三线合一”及三角函数可求得P1P2 = 2asin α.
则△PAB的周长的最小值为2asin α.
让我们再来解决下面这道题.
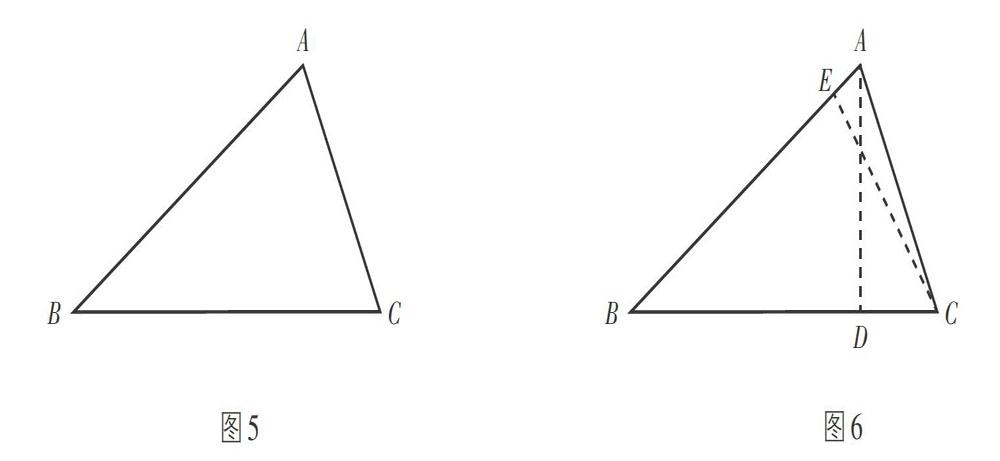
回归原题:如图7,在线段BC上任取一点P,分别作点P关于AB,AC的对称点P1,P2,连接P1P2,“分别交AB,AC于Q,R”,
则△PQR周长 = P1P2.
其中△AP1P2是等腰三角形,腰长P1A = P2A = AP,顶角∠P1AP2 = 2∠BAC.
再回头看一下问题1和问题2,可得到P1P2 = 2AP × sin∠BAC.
因为sin∠BAC是定值,所以当AP的值最小时△PQR的周长最小.
由“垂线段最短”可知,点P与点O重合(AP = AO)时AP的值最小,本题中AO是定值,sin∠BAC是定值,至此问题得到解决.
[ 原题延伸]
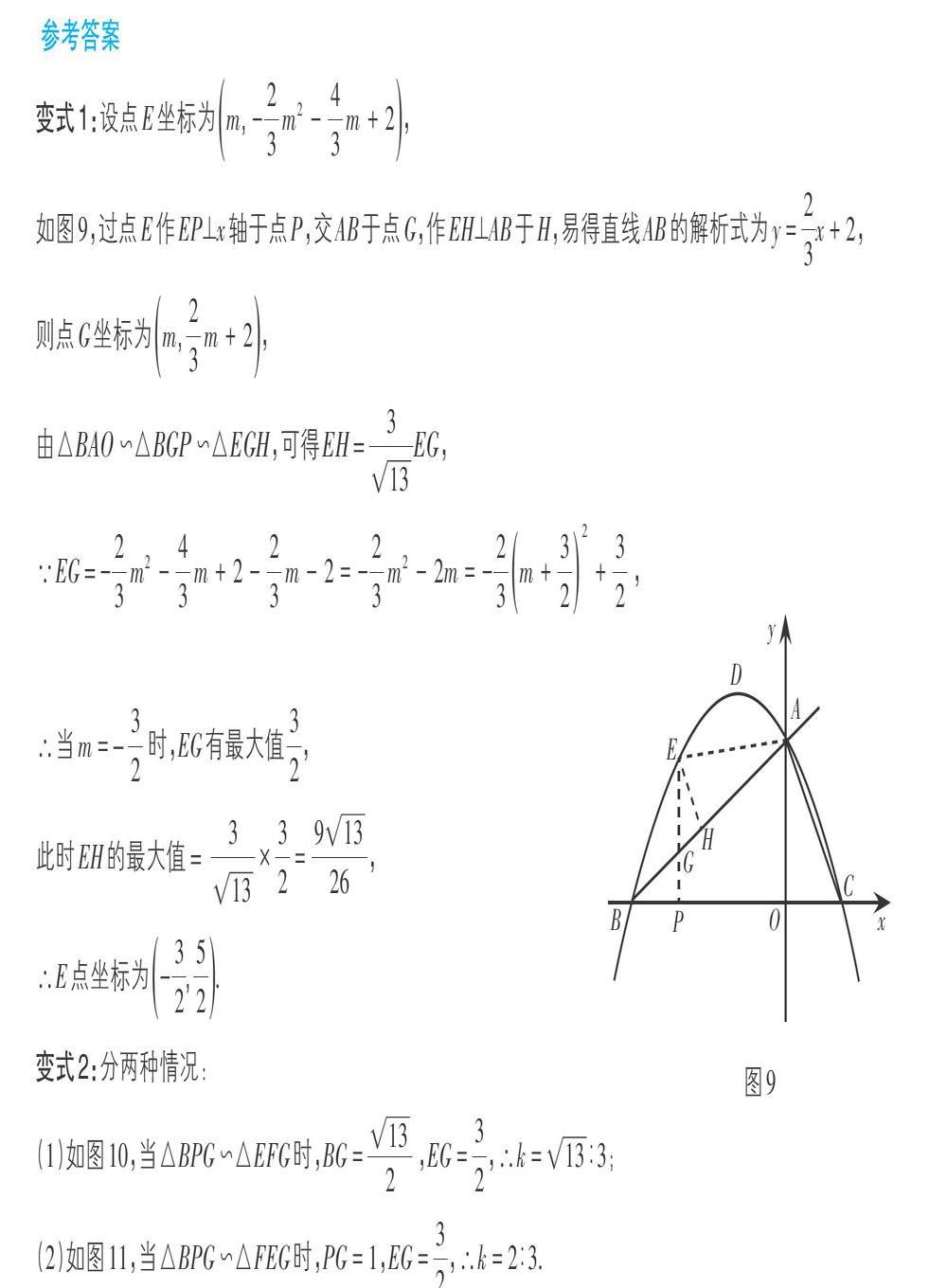
针对例题第(2)问可以做以下变式:
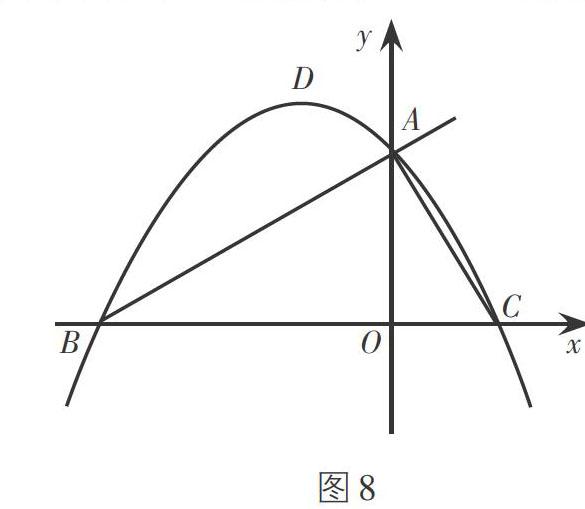
变式1:如图8,点E是直线AB上方的抛物线上一点,若使四边形AEBC面积最大,求点E的坐标.
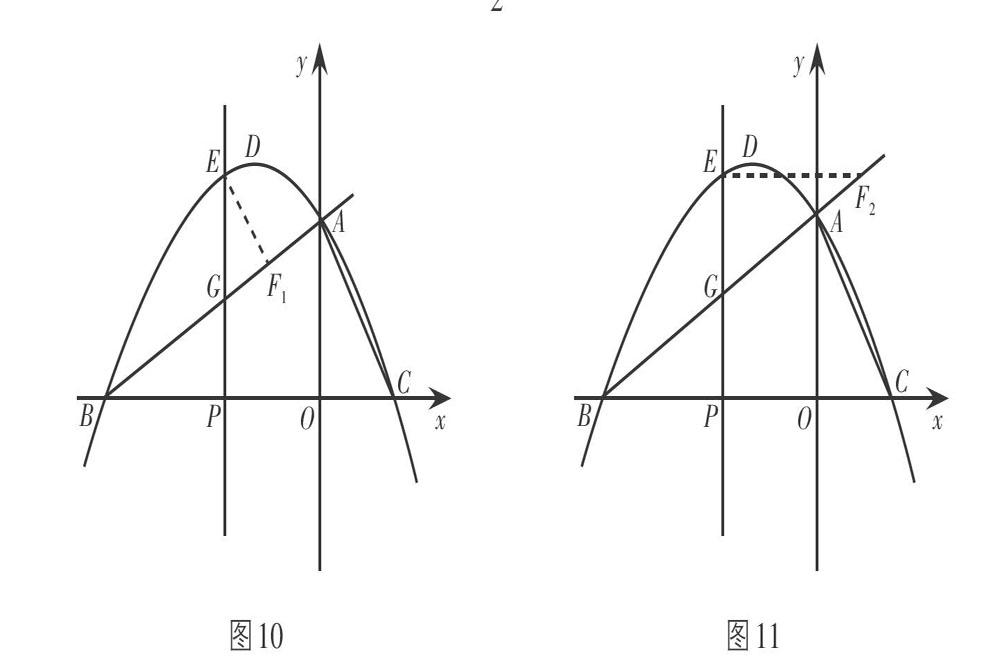
变式2:在变式1的条件下,过点E作EP⊥x轴于点P交AB于点G,在直线AB上找一点F,使△BPG与△EFG相似,且相似比為k,请直接写出k的值.
