大跨度独塔斜拉桥地震响应分析

谢波，石琦，谭皓

（1.中交路桥华南工程有限公司，广东 中山528400；2.长沙市望城区公路管理局，长沙410200）

1 引言

对桥梁进行抗震分析的方法有很多种，其中比较常见的便是反应谱法和时程分析法。对于特大桥，采用单一的分析方法通常不够准确。为了探究2种分析方法之间的差异，本文以某独塔斜拉桥为工程实例进行模拟分析，得到的结论可以供其他特大桥做参考。

2 工程概况

某独塔斜拉桥是一座主梁非对称的独塔斜拉桥，塔、梁、墩为固结的刚构体系。斜拉索采用双索面。主塔每侧设26对斜拉索，斜拉索在主梁上的基本索距为7 m，边跨尾索区长度为4.5 m；塔上索距为2 m，全桥共104根斜拉索。主塔设计为钻石形，由下、中、上塔柱及下横梁组成，主塔总高度为127.586 m，其中，下塔25.236 m、中塔59.84 m、上塔42.51 m，采用C50混凝土施工。主梁设计为单箱三室预应力混凝土箱梁结构，斜拉索布置方式为扇形布置。特征周期为0.35 s，场地类型划分为Ⅱ类，抗震设防烈度为7度。

3 有限元模型的建立

本文对独塔斜拉桥的主梁采用脊梁模式进行模拟[1]，主塔采用三维梁单元，斜拉索采用桁架单元，主塔底部直接采用固结方式进行模拟。主梁与主塔之间进行固结，斜拉索与主梁之间采用附加刚臂进行连接。模型共建有400个节点，292个单元。其有限元模型如图1所示。

图1 独塔斜拉桥有限元模型示意图

4 反应谱加速度的确定与时程函数的选取

4.1 反应谱加速度的确定

对于反应谱加速度的确定，根据JTC/T 2231-01—2020《公路桥梁抗震设计细则》（以下简称《细则》）[2]中的5.2.1条款确定水平设计加速度反应谱的主要参数，如表1所示。阻尼比的变化会显著改变反应谱值，从而影响结构所受地震力的大小[3]。斜拉桥的阻尼比通过规范查知，一般不应大于0.03，对于本文所研究的独塔斜拉桥，阻尼比取0.02。《细则》5.2.4规定，当结构的阻尼比不等于0.05时，应调整阻尼调整系数Cd。

表1 水平设计加速度反应谱系数取值表

4.2 时程函数的选取

时程函数的确定过程中，需要解决的问题比较多，主要是地震波的选取和阻尼问题。

对于地震波的选取，可参考文献[4]和文献[5]。阻尼不会引起振型耦合，所有2个振型频率阻尼比是相同的，即ξi=ξj=ξ（其中，ξi和ξj分别为不同振型的阻尼比；ξ为一阶频率对应的阻尼比）。通常钢结构的阻尼比为2%，混凝土结构取5%，如果它们混合使用，则阻尼比取值应在2%～5%。以ωi为结构的基频；ωj取后面几阶中对结构振型贡献最大的模态频率。由于在桥梁结构中，低阶频率对桥梁的振动贡献较大，所以，ωi和ωj分别取第一阶频率和二阶频率[6]。

最后求得阻尼系数a1、a2，见表2。

表2 2个模型的阻尼系数统计表

5 反应谱法与时程分析法计算结果对比

对于独塔斜拉桥，其峰值主要产生在主塔塔顶、塔根以及主塔跟主梁连接位置，主梁产生的峰值主要在支座和跨中。所以，本文对于主塔和主梁的典型截面位置如图2、图3所示。

图2 主塔的典型截面位置

图3 主梁的典型截面位置

5.1 位移结果对比

如图4所示，在2种地震反应分析方法下发现，主塔的纵向位移都在塔顶1#处最大，采用反应谱分析方法时，1#位置处最大纵向位移为29.12 mm；采用时程分析法时，1#位置处最大纵向位移为32.16 mm，时程分析得到的位移比反应谱分析得到的位移大3.04 mm。主梁的纵向位移都在梁端7#位置处达到最大，采用反应谱分析法时，7#位置处最大纵向位移为16.33 mm；采用时程分析法时，7#位置处最大纵向位移为15.21 mm，反应谱分析得到的位移要比时程分析得到的位移大1.12 mm。横向位移几乎都没有明显变化这说明在纵向和竖向作用下，横向几乎不受其影响。竖向在主跨中间8#位置处产生最大位移，反应谱分析方法下8#最大竖向位移为35.91 mm，时程分析法下8#位置处最大竖向位移为40.03 mm，时程分析得到的位移比反应谱分析得到的位移大4.12 mm。

通过对2种方法的分析结果进行对比分析可知，其位移峰值所产生的部位都是一样的，只是位移大小有细微差别，差值都在20%以内，符合规范要求。这表明2种方法对比模拟分析，可以互相校核，为抗震设计提供更加准确的信息。

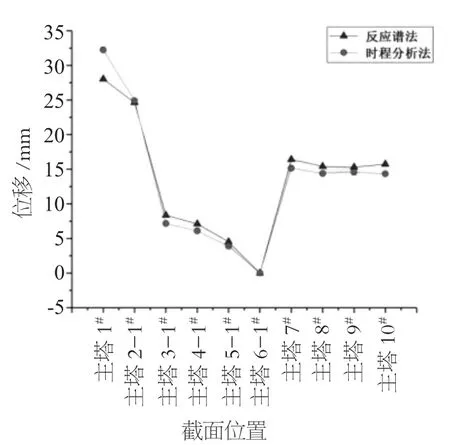
图4 纵向位移对比图

5.2 内力结果对比

在2种分析方法下，其内力也在相同位置达到峰值。如图5和图6所示，主塔塔根6-1#截面处的剪力达到最大，采用反应谱法时，6-1#截面的剪力最大为12 110.31 kN，弯矩最大为270 333.18 kN·m；采用时程分析法时，6-1#截面剪力最大为10 949.23 kN，弯矩最大为240 115.18 kN·m。反应谱法分析得到的内力要比时程分析法得到的大。主梁都在副主跨中间9#截面达到峰值，采用反应谱法时，9#截面剪力最大为3 799.67 kN，弯矩最大为45 419.43 kN·m；采用时程分析法时，9#截面剪力最大为4 196.24 kN，弯矩最大为50 231.75 kN·m。时程分析法得到的内力要比反应谱法分析得到的大。

通过比较发现，采用2种分析方法得到的主塔塔根内力均远比主梁内力大，这表明在实际抗震设计中，主塔塔根是受力薄弱处，需要加强设计。而在内力数值上，反应谱法分析得到的主塔内力比时程分析法得到的内力大；而对于主梁内力，时程分析法得到的结果比反应谱法的结果大。所以，只有将二者进行对比，才能得到可靠的分析。

图5 剪力Q z对比图

图6 弯矩M y对比图

6 结论

以某大跨度独塔斜拉桥为工程实例，利用Midas/Civil软件分别采用反应谱法与时程分析法进行该桥的位移与内力对比分析，得出结论如下：

1）采用2种分析方法计算出来的结构位移和内力在数值上有所偏差，但是差值都在20%以内，符合国家抗震规范要求；位移和内力计算结果趋势基本一致，所产生的峰值截面相同，2种分析方法分析得到的结构内力及位移都可以比较真实地反映地震作用下的结构反应。

2）反应谱法所产生的位移在主塔上比时程法分析得到的结果偏大，但是在主梁上要偏小，对于内力而言，反应谱分析所产生的内力普遍比时程分析产生的大，所以，进行结构抗震设计时，不能单一地使用一种方法进行分析，应合理运用这2种方法，为了桥梁的使用安全，可以将反应谱分析法当作一种估算的方法来控制截面，然后再用时程分析方法进行校核。