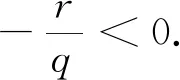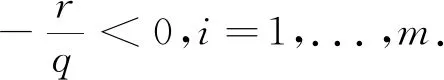含有不等式约束的全局优化问题的一种新的辅助函数法
2021-06-05王倩
王 倩
(四川文理学院 教务处,四川 达州 635000)
无约束的或者箱子集约束的全局优化问题有很多学者已经在不断研究与改进,如文献.[1-7]其中打洞函数法最早是于1985年在文献[2]中提出的,其打洞函数为:
该方法要求f(x)在X上二次连续可微,并且假设函数f(x)只有有限个孤立的极小点.
后来,Ge.R.P在文献[3]中提出了另一类求解一般非线性规划问题的全局最优解的辅助函数法:填充函数法.文献[3]中给出填充函数的基本思想是:通过极小化填充函数跳出当前的局部极小点,因而找到一个目标函数值比当前函数值更小的点,循环运算直至找到全局极小点.因该填充函数受到指数项的影响,会找到假的平稳点,因此丢失目标函数的全局最优解.
后来很多学者对其做了改进工作,如文献.[4-8]特别在文献[8]中提出的新的辅助函数法,无论在理论性质还是数值试验结果上,较之前的辅助函数都有非常突出的优越性.然而文献[8]中提出的新辅助函数法只是用于求解一般无约束的全局优化问题.而对于有约束的全局优化问题的研究,特别是含有不等式约束的全局优化问题的研究,是非常具有现实意义和研究价值的.在文献[1]中Wu Z.Y.等提出了一种求解含有不等式约束的全局最优解的辅助函数法,其在理论性质和数值试验结果上都有非常突出的优越性,但其不能保证平稳点函数的局部极小点是原问题的局部极小点,所以每次求解平稳点函数的局部极小点以后,还需要重新求解原问题的局部极小点.本文结合文献,[1],[8]提出了一种新的改进填充函数法,用于求解含有不等式约束的一般非线性规划问题的全局最优解.
新的改进填充函数及其性质
本文考虑如下问题(P)[1]
其中,f(x)和gi(x)在Rn→R上连续可微,i=1,...,m,.
假设1f(x)满足强制性条件:当‖x‖→+∞时,f(x)→+∞.
假设2 问题(P)的局部极小值的个数为有限个.
令
S={x∈X|gi(x)≤0,i=1,...,m},
S0={x∈intX|gi(x)<0,i=1,...,m}.(2)
假设3S0为非空集,clS0=S.
本文假设x*为当前原问题(P)的局部极小点.
定义1 函数T(x,x*,r)称为含有不等式约束全局优化问题(P)的改进填充函数,如果T(x,x*,r)满足如下条件:
1)对任意的x∈S,0
2)设x*是f(x)的一个局部极小点,则∃q>0,对任意的0 3)对任意的0 4)对任意的x∈L2={x|f(x) 5)对任意的x1,x2∈S0,若f(x1)≥f(x*),f(x2)≥f(x*),则‖x2-x*‖>‖x1-x*‖当且仅当T(x2,x*,r) 下面给出一种改进的填充函数 其中0 很容易验证φr(t)≥0,ψr(t)≥0,且连续可微. 下面的定理表明,当参数r,q满足某些条件时,本文构造的辅助函数T(x,x*,r)满足定义1给出的改进填充函数的定义. 定理1 对任意的x∈S,0 证明:必要性(⟹) 充分性(⟸) 因为f(x)-f(x*)+r=0,所以φr(f(x)-f(x*)+r)=0.对任意的0≤r<1,∃q>0, 证毕 定理2 设x*是f(x)的一个局部极小点,则∃q>0,对任意的0 证明:因为x*是一个局部极小点,则∃δ>0,对∀x∈ο(x*,δ)∩S0,有f(x)≥f(x*), 所以f(x)-f(x*)+r≥0+r>0, 故T(x*,x*,r)>T(x,x*,r),即x*是T(x,x*,r)的一个严格局部极大点. 证毕 定理3 对任意的0 证明:由(3)式知 定理4 对任意的x∈L2={x|f(x) 证明:当f(x) f(x)-f(x*)+r<0,则有T(x,x*,r)=r(f(x)-f(x*)+r)3. 这时∇T(x,x*,r)=3r·(f(x)-f(x*)+r)2∇f(x),因为f(x)-f(x*)+r<0, 所以∇T(x,x*,r)与∇f(x)同号,从而T(x,x*,r)和f(x)的单调性保持一致. T(x,x*,r)的局部极小点. 证毕 定理5 对任意的x1,x2∈S0,若f(x1)≥f(x*),f(x2)≥f(x*),则‖x2-x*‖>‖x1-x*‖当且仅当T(x2,x*,r) 证明:因为对任意的x1,x2∈S0,若f(x1)≥f(x*),f(x2)≥f(x*),则 所以,‖x2-x*‖>‖x1-x*‖当且仅当T(x2,x*,r) 定理5保证了辅助函数在极小化搜索过程中,不会再回到原来极小点所在的盆谷中. 由以上的定理及定义1可以得到,当参数r和q满足一定条件时,函数T(x,x*,r)是点x*处的新的改进填充函数. 由于文献[8]中的辅助函数算法在数值实验结果中有较为突出的有效性,因此,可借鉴该算法进行推广,在数值试验中可进行有效性的检测.