基于一种新的优势关系的多属性决策方法
2021-06-05黄贤峰
黄贤峰
(湖北民族大学 数学与统计学院,湖北 恩施 445000)
多属性决策(Multi-attribute decision making,MADM)问题是指在考虑多个属性的情况下,选择最优方案和对方案进行排序的决策问题,是现代决策科学的重要组成部分.
随着MADM的发展,一系列的决策方法相继提出,如TOPSIS方法[1]、VIKOR方法[2]、WAA方法[3]、ELECTRE方法[4]和TODIM方法[5]等.其中,TOPSIS方法是一种逼近正理想解的决策方法,借助多属性决策问题中的正理想解(positive ideal solution,PIS)和负理想解(negative ideal solution,NIS)实现排序,但这种方法仅仅考虑到每个备选方案与PIS间的关系,存在一定的局限性;VIKOR方法注意到TOPSIS方法的这种不足.因此,VIKOR方法的优势在于同时考虑了每个备选方案与PIS和NIS之间的距离.此外,这些经典的决策方法被进一步推广到不同的决策背景,从而建立了基于不同决策背景的多属性决策模型.如基于模糊集的多属性决策模型[6]、基于犹豫模糊集的多属性决策模型[7]、基于直觉模糊集的多属性决策模型[8]和基于语言术语集的多属性决策模型[9]等.同时,多属性决策理论广泛应用于各个领域,如供应链选择[10]和人才选拔[11]等.然而,这些经典的决策方法或多或少存在着一些不足,因此,本文将进一步结合优势关系的相关理论对TOPSIS方法进行进一步改进和完善.
在经典粗糙集理论中往往借助等价关系(或不可区分关系)对各个备选方案进行研究.然而,在实际应用中这种关系往往过于严格且不具有容错性,不能有效地解决问题.因此,Greco等[12]提出了基于优势关系的粗糙集理论,其主要利用优势关系代替条件属性集或决策属性集上的等价关系,但依然保持经典粗糙集的主要性质.在优势关系的发展过程中,也衍生出许多研究成果,如Huang Q Q等[13]构造一种基于复合优势关系的粗糙集模型,Chakhar等[14]提出了基于优势关系的粗糙聚合方法,Du W S和Hu B Q[15]建立了不完备序信息系统下基于优势关系的粗糙集模型.这些研究成果推动了优势关系在粗糙集领域的发展.因此,本文将基于优势关系提出一种新的决策方法从全局的角度判断出各方案的优劣.
本文的组织结构如下:第1节简要回顾了与多属性决策背景相关的基本概念和表示;第2节提出了基于优势关系的多属性决策方法;第3节对所提出的决策方法进行了实验分析,验证了所提方法的合理性和有效性;第4节总结全文并提出未来可以研究的方向.
1 预备知识
主要介绍模糊信息系统(或模糊知识表达系统)和TOPSIS(technique for order preference by similarity to ideal solution)方法的一些基本概念和表示.
1.1 模糊信息系统
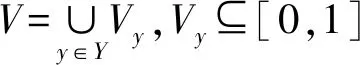
模糊信息系统的数据常以关系表的形式给出.其中,关系表的行对应要研究内容的对象,列对应要研究内容的属性,对象的各属性值表示各对象的信息.
1.2 TOPSIS法
TOPSIS法[1]是一种逼近PIS的排序方法,它借助多属性问题的PIS和NIS对方案集X中各方案排序.PISx+和NISx-都是方案集X中并不存在的虚拟的方案.其中,PISx+是方案集中虚拟的最佳方案;而NISx-是方案集中虚拟的最差方案.通过对方案集X中各方案和PIS及NIS的距离来进行比较,即对于方案集中既靠近PIS又远离NIS的方案为最佳方案.
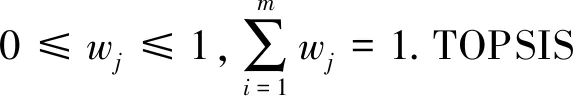
步骤1 求规范决策矩阵.设多属性决策问题的决策矩阵为Y=(yij)n×m,则规范化决策矩阵Z=(zij)n×m.其中,
(1)
步骤2 构成加权规范化矩阵X=(xij)n×m.
xij=wj·zij,i=1,2,…,n;j=1,2,…,m.
(2)
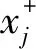
(3)
步骤4 计算各方案到PISx+和NISx-的距离.
备选方案xi到PISx+的距离为:
(4)
备选方案xi到NISx-的距离为:
(5)
步骤5 计算各方案的综合评价值ηi.
(6)
步骤6 根据各方案的综合评价值ηi由大到小进行排序.
1.3 熵权法
在1.2节主要讨论TOPSIS方法的计算过程,然而没有给出具体求权重的方法.为了确保属性权重的合理性和准确性,本文将采用熵权法[16]对属性权重进行计算,具体计算如下:
(7)
其中,zij表示规范化决策矩阵Z=(zij)n×m的元素,n表示备选方案的个数.通过该方法求出的权重相较于主观权重更加合理,有效地减少了决策者自身偏好的影响.
2 基于优势关系的决策方法
随着MADM问题研究的不断深入,一系列经典的MADM方法相继提出[1-5].然而,这些MADM方法仍然存在着诸多的缺陷,如考虑角度较局限,参数过多等.为了完善所存在的不足,本文将基于TOPSIS方法建立一种新的优势关系,进而提出一种新的决策方法.
2.1 基于TOPSIS方法的优势关系
TOPSIS方法,只考虑到所评价方案与PIS的距离,而忽略了与NIS的距离.同时,考虑到优势关系相较于经典粗糙集理论中的等价关系而言,比较宽松和具有容错性,因此,本文将结合TOPSIS方法建立一种新的优势关系.
定义2 设X={x1,x2,…,xm}是一个有限非空备选方案集,Y={y1,y2,…,ym}是一个属性集.对于两个方案xi和xj,若xi的综合评价值不低于xj的综合评价值,则认为方案xi优于xj,记作xiR≻xj;相反地,若xi的综合评价值不高于xj的综合评价值,则认为方案xi劣于xj,记作xiRxj.即:
R≻={(xi,xj)∈X×X|ηi≥ηj},
R={(xi,xj)∈X×X|ηi≤ηj}.
(8)
分别表示优势关系和劣势关系.
定义3 根据定义2所定义的优势关系R≻和劣势关系R,可以进一步定义xi∈X的优势集和劣势集分别为:
[xi]R≻={xj|xiR≻xj∧xj∈X},
[xi]R={xj|xiRxj∧xj∈X}.
(9)
如果xj∈[xi]R≻,即xiR≻xj,说明xi优于xj.同样地,如果xj∈[xi]R,即xiRxj,说明xi劣于xj.
例1 一个投资公司打算选择一些投资项目来利用其闲置的资金,有8个备选投资项目.其中,3个高科技项目(x1,x2,x3),3个互联网项目(x4,x5,x6),2个文化教育项目(x7,x8).决策者将根据预期效益(y1)、环境影响(y2)、市场饱和(y3)、社会效益(y4)和节能(y5)这5个标准对备选投资项目进行评价.显然,预期效益、社会效益和节能是效益标准.环境影响和市场饱和是本例中的成本标准.各属性评价值为0和1之间的数.评价结果见表1.
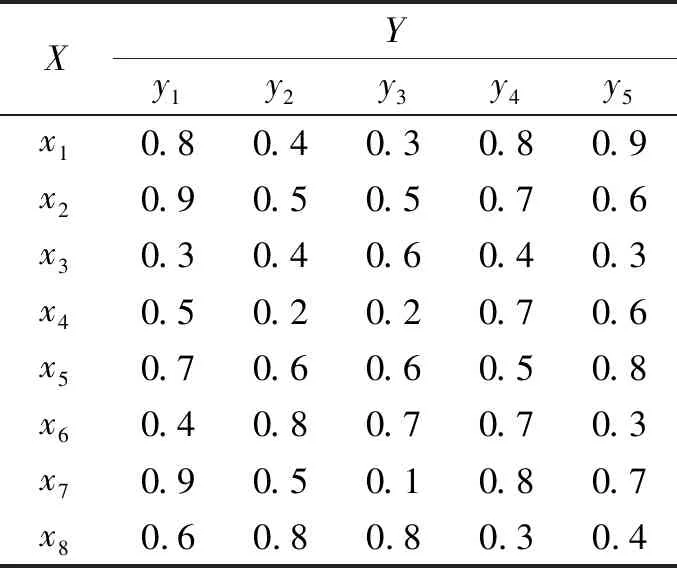
表1 评估矩阵Tab.1 Evaluation matrix
根据式(7)可知属性权重向量为w={0.152 5 0.183 5 0.363 3 0.118 3 0.182 3}.同时,由式(4)和式(5)知方案xi(i=1,2,…,8)到PIS和NIS的距离如表2所示.

表2 方案xi(i=1,2,…,8)到PIS和NIS的距离Tab.2 Distance of alternative xi(i=1,2,…,8) to PIS and NIS
根据式(6)可知方案xi(i=1,2,…,8)的综合评价值分别为0.746 8,0.505 5,0.303 5,0.739 4,0.406 7,0.181 1,0.140 5.同时,根据定义2和定义3,有:
[x1]R≻={x1,x2,x3,x4,x5,x6,x8},[x1]R={x1,x7},
[x2]R≻={x2,x3,x5,x6,x8},[x2]R={x1,x2,x4,x7},
[x3]R≻={x3,x6,x8},[x3]R={x1,x2,x3,x4,x5,x7},
[x4]R≻={x2,x3,x4,x5,x6,x8},[x4]R={x1,x4,x7},
[x5]R≻={x3,x5,x6,x8},[x5]R={x1,x2,x4,x5,x7},
[x6]R≻={x6,x8},[x6]R={x1,x2,x3,x4,x5,x6,x7},
[x7]R≻={x1,x2,x3,x4,x5,x6,x7,x8},[x7]R={x7},
[x8]R≻={x8},[x8]R={x1,x2,x3,x4,x5,x6,x7,x8}.
2.2 相对优于度
为了进一步从全局角度对每个方案进行研究,本文将在2.1节所定义优势集和劣势集的基础上,进一步定义每个方案的相对优于度.
定义4 设(X,Y)是一个模糊信息系统,[xi]R≻和[xi]R分别表示方案xi∈X的优势集和劣势集.则方案xi(i=1,2,…,n)的相对优于度(relative superior degree,RSD)为:
(10)
其中,|*|表示集合*的基数.且RSD(xi)表示方案xi∈X优于其他方案的相对程度.因此,RSD(xi)越大,说明方案xi越优.
例2(例1续) 根据例1,得出每个方案的优势集和劣势集,进而可以借助定义4计算出每个方案的相对优于度.计算结果如表3所示.
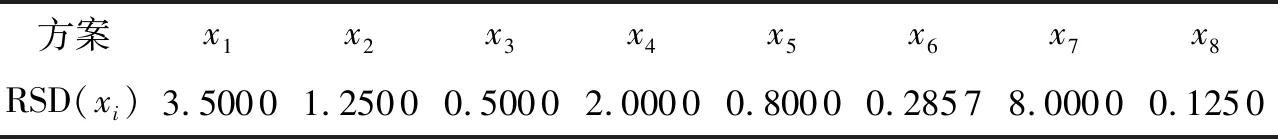
表3 方案xi(i=1,2,…,8)的相对优于度Tab.3 Relative superiority of scheme xi(i=1,2,…,8)
根据表3,有8.00 0>3.500 0>2.000 0>1.250 0>0.800 0>0.500 0>0.285 7>0.125 0,则:
x7>x1>x4>x2>x5>x3>x6>x8.
因此,按照相对优于度大小得出的最优方案为x7.
3 实验分析
为了说明所提出方法的合理性和有效性,本文将进一步将所提方法和经典的决策方法进行比较分析,如TOPSIS方法,VIKOR方法和WAA方法等.同时,为了进一步说明所提出方法的有效性,本文将选取UCI数据库(http://archive.ics.uci.edu/ml/)中的两个数据集(Algerian Forest Fires和Lymphography)进行数据集实验.
3.1 比较分析
MADM作为一门成熟的领域,目前提出了一系列合理且有效的决策方法.因此,为了说明所提方法的合理性,本文将所提方法和3种经典决策方法(TOPSIS方法[1]、VIKOR方法[2]和WAA方法[3])进行比较.得到的排序结果如表4所示.根据表4,可以看出本文所提出的方法和经典决策方法的排序结果类似,但本文所提出的方法相较于经典决策方法考虑得更具有全局性,不单单考虑每个备选方案自身的因素.因此,本文所提出的方法存在着一定的合理性,可以有效地实现对所有方案的排序.

表4 不同方法的排序结果Tab.4 Ranking results of different methods
3.2 数据集实验
为了进一步说明所提方法的有效性和优越性,本文将借助UCI数据库(http://archive.ics.uci.edu/ml/)中的两个数据集(Algerian Forest Fires和Lymphography)进行数据集实验.对于Algerian Forest Fires而言,根据实验需要仅保留4个属性:正午温度 (效益型属性),相对湿度 (成本型属性),风速(成本型属性) 和降水量(成本型属性).同时,对于Lymphography数据集而言,保留属性lymphatics,lym.nodes dimin ,lym.nodes enlar ,changes in lym,defect in node,changes in node and special forms,且均为成本型属性.实验结果和最优方案如图1和表5所示.
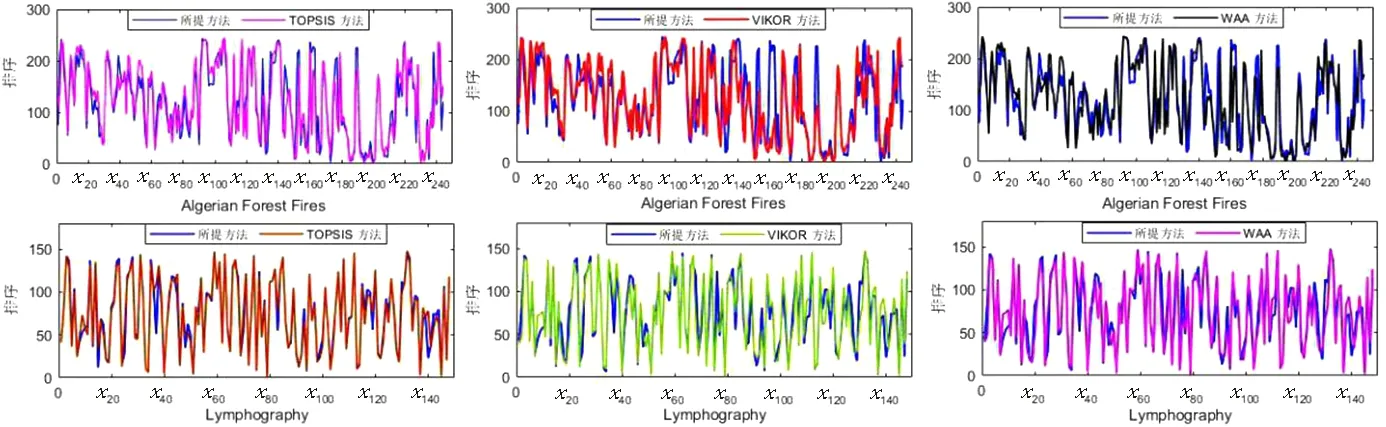
图1 数据集Algerian Forest Fires和Lymphography对比结果Fig.1 Comparison results of data sets Algerian Forest Fires and Lymphography

表5 不同数据集在不同决策方法下的最优方案Tab.5 Optimal solutions for different data sets under different decision methods
从图1可以看出,本文所提方法所得实验结果和经典的决策方法非常相似.同时,借助表5可知最优方案完全一致,充分说明本文所提方法的有效性和合理性.此外,相较于经典决策方法只单纯从每个方案自身出发,考虑自身的优越性,而未考虑到各方案与其他方案之间的联系.因此,基于两个数据集实验可以看出本文所提决策方法的有效性和优越性.
4 结论
基于TOPSIS方法,提出了一种新的多属性决策方法.通过考虑各方案与其他方案之间的关系,从全局的角度对每个备选方案进行综合评价.通过案例分析和实验分析对所提方法的合理性和有效性进行验证.同时,本文的主要贡献如下:
1) 基于TOPSIS方法,本文定义了一种新的优势关系和劣势关系,可以有效地避免不可区分关系过于严厉和不具有容错性的缺陷.
2) 通过借助优势关系和劣势关系从全局角度对每个备选方案进行研究,可以有效考虑到各方案与其他方案之间的关系,更高效的实现决策.
此外,考虑到MADM的发展,在未来的研究中,可以进一步将本文所提出的方法结合不同的信息系统下展开研究,如直觉模糊信息系统[17]和不完备信息系统等.同时,可以结合机器学习[18]、主动学习[19]及概念分析[20]等领域展开研究.
