高速铁路跨线列车运行路径 选择优化模型

闫绍辉，张天伟，董隆健

（1.中铁工程设计咨询集团有限公司 郑州设计院，河南 郑州 450000；2.石家庄铁道大学 交通运输 学院，河北 石家庄 050043；3.中国铁路郑州局集团有限公司 郑州站，河南 郑州 450000)

随着我国高速铁路的快速发展，高速铁路路网在不断完善，跨线客流出行需求日益增加。错综复杂的路网结构使得路网中同一OD之间存在着多条有效可达路径，不同的跨线列车运行路径方案对高速列车运输组织的影响程度也不同[1-2]，因而跨线列车运行路径选择成为列车运行组织研究的重要环节[3-4]。通过对车流路径[5-6]和站场咽喉布置[7]相关文献的查阅可知，高速铁路跨线列车选择从路网中某一车站完成跨线作业时，不仅需要考虑车站内设备规模[8]和区段线路通过能力[9]的影响，还需要考虑在车站跨线作业的难度和可能性，因而从车站和区段2方面入手构建高速铁路跨线列车运行路径选择优化模型，并通过实例对模型进行验证，为铁路企业制定跨线列车运行方案提供借鉴。

1 列车运行路径选择优化问题提出

高速铁路总里程的增加，使得我国高速铁路的路网结构从单一线型结构逐渐发展到如今复杂的网状结构，连接各个城市节点的线路也不再唯一，列车运行径路的选择呈多样化发展。列车运行路径选择优化问题是在车站间连接线路均是已有且不能够任意添加线路的基础上，对车站和区间线路重新进行筛选组配，从而找出最优的跨线列车运行路径方案。对于高速铁路跨线列车运输而言，运行路径最短并非是最优、最符合实际情况的方案，这是由于不同车站内不同的运行线路方向对高速列车在站内作业难度和时间的影响程度是不同的，因而该问题是一个时间、距离、影响能力等多个因素共同影响的多目标线性规划问题。

列车运行路径选择问题是对路网中各个车站和区段线路的选择优化，因而需要从车站和区段2个角度对该问题进行分析。根据目前已运营的高速铁路路网的结构，车站在路网中的连接形式主要有车站连接2个运行方向、车站连接3个运行方向、车站连接4个运行方向3种。对于车站连接2个运行方向形式而言，由于车站连接的线路都在同一高速铁路，在路网中只起到中间站的作用，因而列车在该站无跨线作业。因此，主要研究车站连接3个运行方向和连接4个运行方向下的跨线运输情况。无论是哪种连接形式，列车在站内跨线难度与连接线路方向和车场之间位置关系有关。选择的2条线路方向位于高速场同侧时，列车接入车站需要在高速场内改变当前运行方向才能发车，此时影响列车跨线主要是换向折返技术作业；若2条线路方向不在车场同侧，列车跨线作业可以通过联络线实现，无需列车换向，因而影响列车跨线主要是站内联络线布置情况[8]。相比较下，前者对站内运输组织的影响大，因而这种情况直接影响着列车在该站跨线的可能性，或者说选择的线路方向是否具备跨线条件要求，如石家庄站除往返北京—德州方面不能够通过跨线列车外，其他线路方向均能够实现跨线；长沙南站除了往返郑州—南昌方面不能通过跨线列车，其他方向均可。因此，列车选择经由某一车站作为途径站前往下一相邻车站时，首先需要根据运行方向与站场的车场位置关系，判断途径站哪些方向允许跨线列车通过，哪些方向跨线存在换向折返技术作业，然后再做选择。

对于区段而言，主要是线路允许通过速度和线路繁忙程度影响着列车在区段运行。考虑到地理位置和修建费用等因素影响，路网中各区段的高速铁路线路所允许通过速度存在差异性，因而不同区段的线路速度要求不一定相同，影响着列车实际运行速度，进而影响列车总运行时间。区段线路跨线列车开行比例能够间接地反映出该区段线路的繁忙程度，如果区段线路每日开行列车比例很大，说明这条线路运能负担大，跨线列车接入的阻碍就越大，列车在车站内选择线路方向应选择繁忙程度较小的区段方向，以缓解该区段线路的运行压力。

2 高速铁路跨线列车运行路径选择优化模型构建

为了更好突出路网点、线间拓扑关系，假定路网中各城市均按一个车站研究，且相邻车站间的区段线路均按一条线路处理，并从车站和区段2个角度着手，分析跨线列车运行路径的选择影响因素，构建高速铁路跨线列车运行路径选择优化模型。

2.1 目标函数分析

以列车运行总距离最短、运行总时间最小和对区段线路通过能力影响最小作为优化目标，构建多目标优化模型如下。

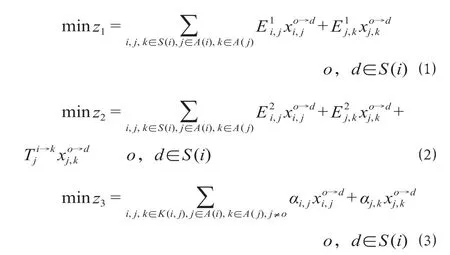
式中：z1表示列车运行总距离，km；z2表示列车运行总时间，min；z3表示运行路径对区段线路通过能力影响值总和；i，j，k，o，d表示路网中客运 站 编 号，i，j，k，o，d∈ {1，2，…，N}；S(i)表示路网中客运站集合；A(i)表示与i站直接相连的客运站集合；A(j)表示与j站直接相连的客运站集合；K(i，j)表示路网中与两相邻i站和j站间线路非同一高速铁路线路的相邻车站集合；分别表示i站到相邻j站的距离、j站到相邻k站的距离，km；为0-1变量，如果始发站为o终到站为d的列车从i站出发后确定选择相邻j站作为下一站，则否则为0-1变量，如果始发站为o终到站为d的列车从j站出发后确定选择相邻k站作为下一站，则否则表示始发站为o终到站为d的列车在i站到相邻j站的区间运行时间，min；表示始发站为o终到站为d的列车在j站到相邻k站的区间运行时间，min；表示从相邻i站到达j站的列车再发往相邻k站时所需要的技术作业时间(主要是指动车组在站内换向折返所需要的时间)，min；αi,j，αj,k分别表示相邻i，j站之间区间线路、相邻j，k站之间区间线路对跨线列车运行的影响程度系数。

公式(1)表示所选择的运行径路总距离最短；公式(2)表示所选择的运行径路总运行时间最小；公式(3)表示所选择的运行路径对区段线路通过能力影响最小。

为了方便计算，通过引入评价函数F将3个优化目标转化为同一个目标，当F值越小，表示该运行路径方案越优。在构建多优化目标的评价函数F时，考虑到3个目标不属于同一量纲，因而在将多个目标转化为单目标之前，通过公式(4)—公式(6)将3个目标函数进行统一化。

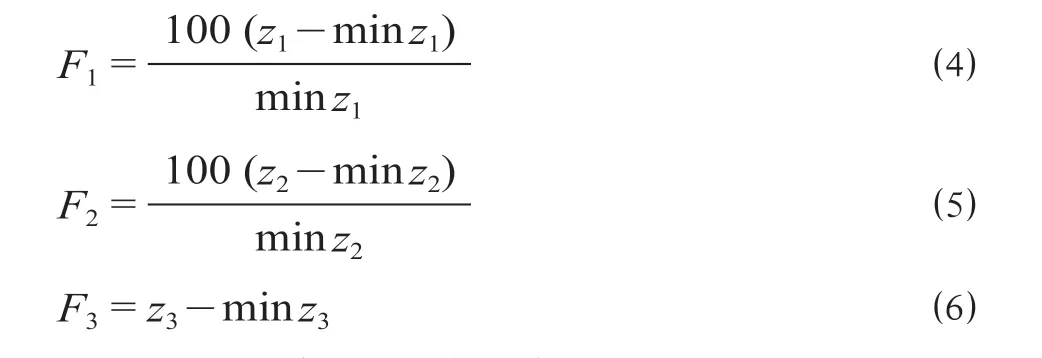
式中：F1表示列车运行总距离评价函数；F2表示列车总运行时间评价函数；F3表示运行路径对区段线路通过能力影响评价函数。

通过线性加和的方法转化成以评价函数总值最小为目标的优化模型为

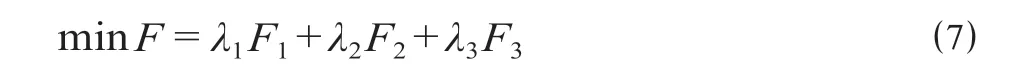
式中：λ1，λ2，λ3分别为运行距离、运行时间和区段线路影响能力在高速铁路跨线列车运行路径评价函数中的权重，其值可利用群决策层次分析法[10]确定。

2.2 约束条件分析

（1）区段线路运行时间。始发站为o终到站为d的列车从i站运行到相邻j站的区间运行时间的计算公式为

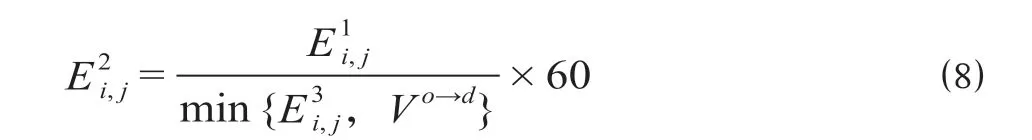
（2）区段线路影响能力。区段线路的影响能力与线路繁忙程度有关，线路越繁忙，列车接入阻碍越大，即对列车运行影响越大。为此，设定参数αi,j的值域为[0，100]，0值表示区段对列车运行没有任何影响，100值表示区段对列车运行影响的最大。定义区段内跨线列车开行最大比值等于0值，区段内跨线列车开行最小比值等于100值，则有以下的等式关系。

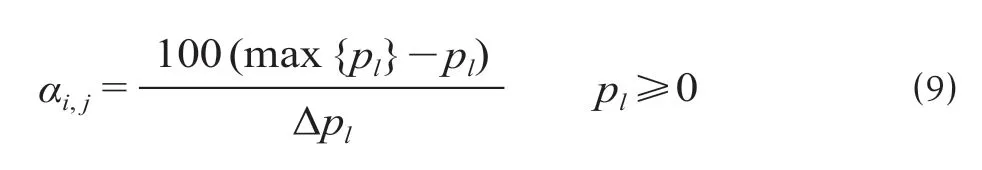
式中：pl为线路区段l中跨线列车开行比例，且l= 1，2，…，M；max {pl}表示线路区段跨线列车开行比例中的最大值；Δpl为pl最大值和最小值的 差值。

（3）变量逻辑约束。路网中3个依次相邻站的连接关系示意图如图1所示，o-j运行方向由o，i，j个依次相邻的车站组成，i-k运行方向由i，j，k3个依次相邻的车站组成。因此，在构建模型时考虑将列车运行径路中3个相邻的客运站i，j，k作为一组进行分析，此时有j∈A(i)，k∈A(j)。

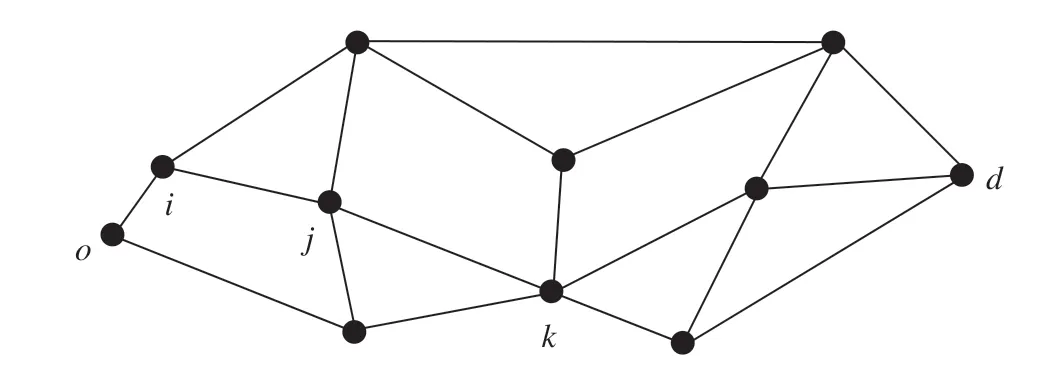
图1 路网中3个依次相邻站的连接关系示意图Fig.1 Connection among three adjacent stations in the railway network

始发站为o终到站为d的列车从i站出发后将相邻j站作为途径车站，同时从j站出发后将相邻k站作为途径车站的变量两者之间存在的逻辑关系约束如下。

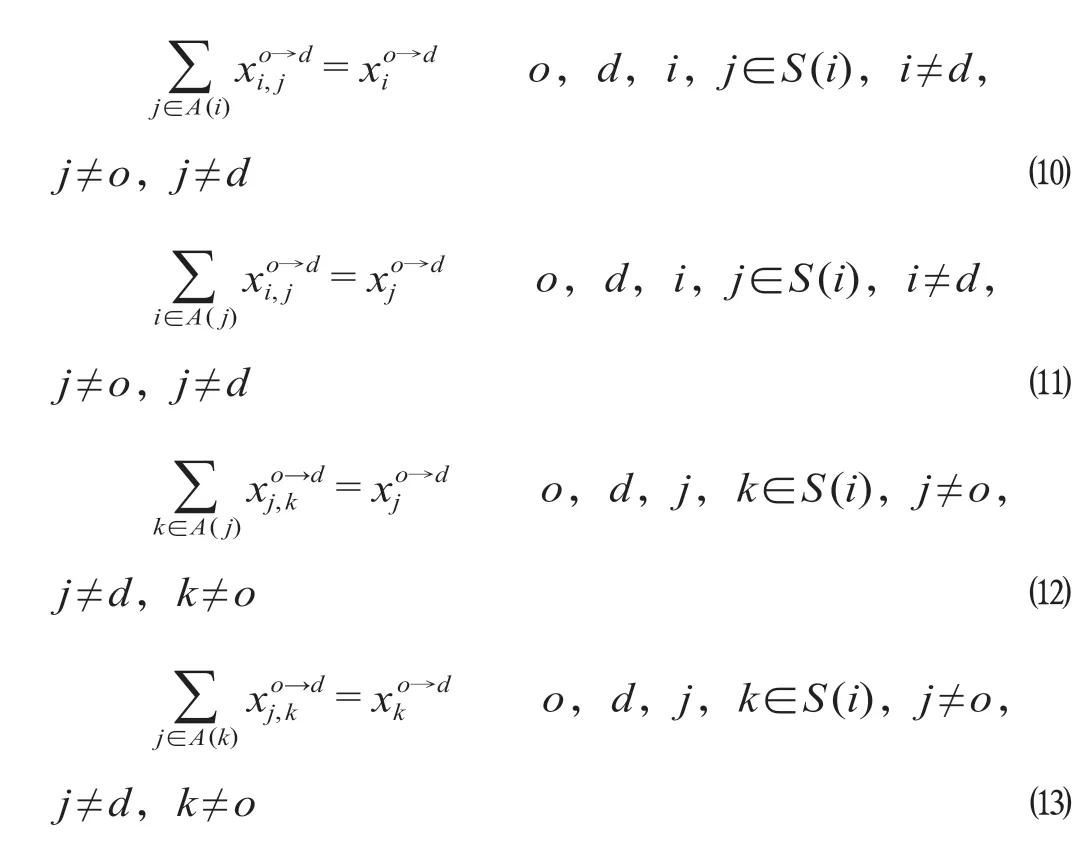
公式(10)表示当列车选择途经i站时，且若从i站出发时，只能在其相邻的客运站中选择1个，否则为0；公式(11)表示当列车选择途经j站时，，所有从与j站相邻的车站出发的列车中必须要到达j站；公式(12)表示列车选择途径与i站相邻j站时，，若列车继续从j站出发时，将只能在与j站相邻的客运站中选择一个作为连接点，否则为0；公式(13)表示当列车从j站选择途经其相邻k站时，且所有从与k站相邻的车站出发的列车中必须到达k站。

在模型迭代计算过程中，通过公式(10)—公式(13)选择相邻车站时，容易出现或者的情况，结合图1可以看出，此时模型判定从i站出发的列车选择其中一个与之相邻j站后，以j站为途径站继续发车，选择与j站相邻的i站又回到i站，接着列车再次重复以上的选择；或者列车从i站出发，到达相邻j站，然后再从j站出发选择下一相邻k站，而在k站选择下一站点时又选择回到j站，相当于列车在j站和k站之间循环运行，或者是列车在i，j，k3站之间反复循环。为了避免列车径路选择时陷入死循环，引入公式(14)和公式(15) 2个约束条件。

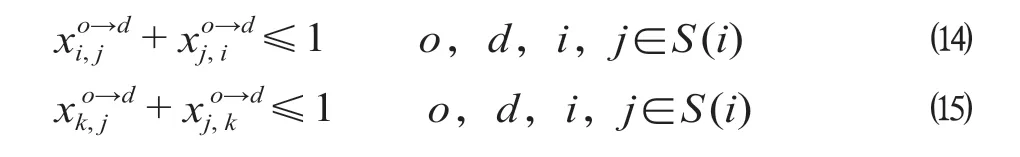
公式(14)和公式(15)的引入，相当于给列车选择路径时增加了一个限制条件，即2个相邻客运站之间的径路，最多只能选择1次，以此避免模型进入死循环，最后出现无解的情况。

（4）跨线决策约束。考虑到在客运站跨线时，有部分衔接线路方向不满足跨线作业条件，因而存在以下约束。

公式(16)表示始发站为o终到站为d的列车若从i站出发后如果选择j站跨线到k站，则需要j站满足从i站到k站的跨线条件，当，表示i-j-k方向是满足跨线条件的，此时列车在j站，是可以选择前往相邻k站这一运行路径。

3 实例应用

跨线列车运行路径方案的编制受路网车站和区段线路的共同影响，为了更全面反映路网结构之间相关关系，以目前已运营高速铁路主要线路为基础，选取具有2个及其以上连接方向或是具备始发终到条件的跨线车站作为模型研究对象，研究跨线列车在路网中实际运行情况。

3.1 模型参数确定

我国高速铁路主要线路路网简化图如图2所示，图2中兰州、太原、昆明、青岛、广州等车站可以作为跨线列车的始发终到站，因而纳入研究范围内，考虑到重庆—武汉区段内的车站没有与其他高速铁路线路相连，因而仅考虑该区段的重庆、武汉2个车站。为方便表示，车站均以所在城市名称代表并顺序编号，路网中车站节点编号如表1所示。

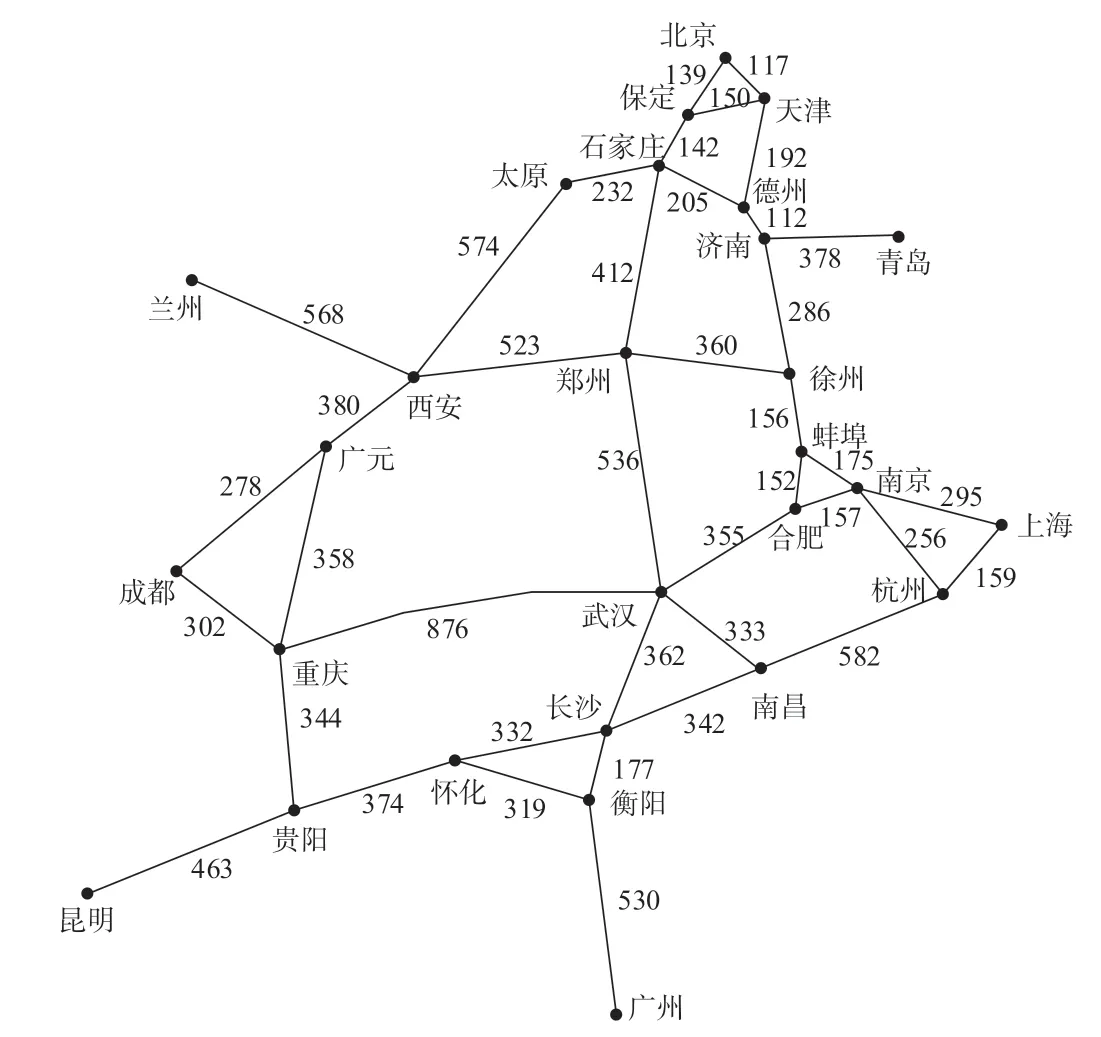
图2 我国高速铁路主要线路路网简化图Fig.2 Simplified railway network of main lines of China’s highspeed railway

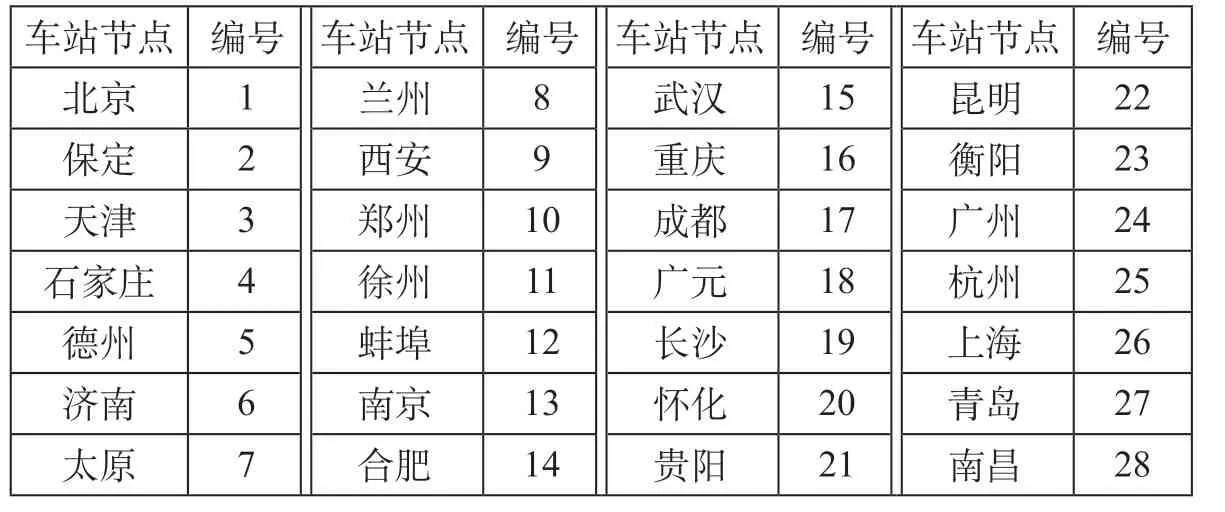
表1 路网中车站节点编号Tab.1 Station node numbering in the railway network

在对模型部分参数量化分析中可知，相邻客运站之间区间线路对跨线列车运行的影响程度系数αi,j值的确定方法。通过对主要高速铁路线路各区段跨线列车开行情况的调研，根据公式(9)即可计算出各区段线路上下行两个方向的影响程度系数αi,j值。但考虑到在实际路网中存在着2个车站间有2条高速铁路线路组成的区段情况，如德州—济南区段、南京—上海区段和成都—重庆区段。为了简化计算，统一将其按一个线路区段处理。我国高速铁路主要线路中各线路区段对跨线列车运行影响值如图3所示。

图3 我国高速铁路主要线路中各线路区段对 跨线列车运行影响值Fig.3 Influence value of each line section in the main lines of China’s high speed railway on cross-line train operation

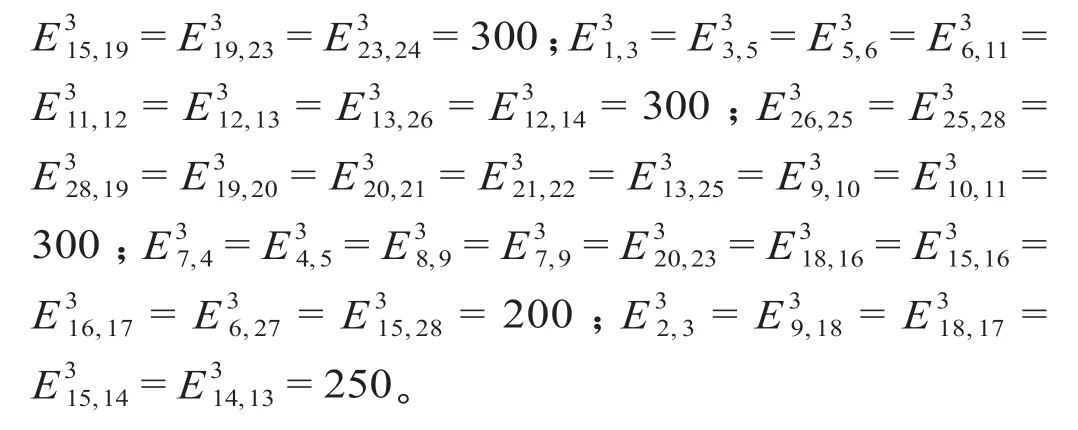
根据图2及表1，分析高速铁路主要线路路网图中各个车站位置和线路连接结构，确定与i站相邻的所有车站集合A(i)如下。

同理，根据图2及表1，可以确定与相邻客运站i，j之间线路非同一高速铁路线路的相邻车站集合K(i，j)，即相对于i，j站的跨线车站集合如下。

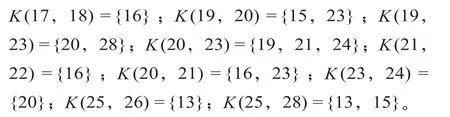
经分析得知，路网中车站内有换向折返技术作业的线路方向有：

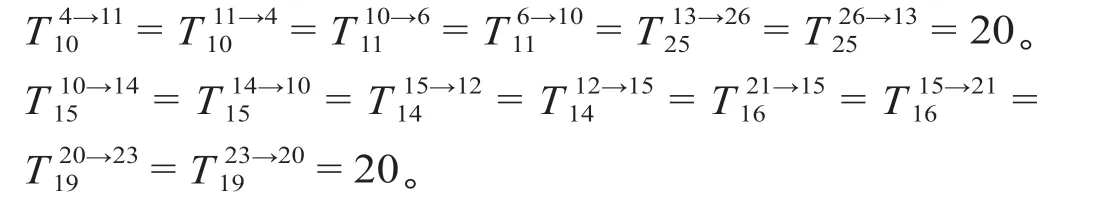
除以上线路方向外，其余各车站其他线路方向均没有换向折返技术作业。定义列车选择没有换向折返作业的线路方向时，在站停留作业时间统一为3 min。

除这些车站的线路方向不能满足跨线列车通过以外，路网中车站其他线路方向均可以通过跨线列车。

根据公式（7），以目标函数F作为目标层，列车运行总距离、运行总时间、区段线路影响能力分别作为指标层，构建高速铁路跨线列车运行路径目标函数评价体系。通过邀请4名铁路方面的专家对列车运行距离、运行时间和区段线路影响3个评价指标进行两两对比打分，通过相应的计算即可得到目标函数中的权重系数为：λ1= 0.366 4，λ2= 0.459 7，λ3= 0.173 9。

3.2 模型求解

根据所研究的路网，把模型中各类参数和部分变量的取值情况确定下来。现选取路网中太原—南京、济南—成都、北京—重庆这3个列车OD作为实例对象，以列车运行速度Vo→d= 300 km/h为例，通过软件对实例进行求解分析。

（1）太原—南京OD跨线列车路径选择。以太原—南京OD为分析对象，则有o= 7，d= 13。求解得到：单独以列车总运行距离最短为优化目标，其最优解为minz1= 1 166；单独以列车总运行时间最小为优化目标，其最优解为minz2= 303.1；单独以区段线路影响最小为优化目标，其最优解为minz3= 64。将3个优化目标值代入评价目标函数中，求解结果如下：其余变量均为0，最优值F= 0。通过模型求解结果可知，太原—南京OD的跨线列车运行路径应选择太原—石家庄—德州—济南—徐州—南京。

（2）济南—成都OD跨线列车路径选择。以济南—成都OD为分析对象，则有o= 6，d= 17。求解得到：单独以列车总运行距离最短为优化目标，其最优解为minz1= 1 825；单独以列车总运行时间最小为优化目标，其最优解为minz2= 495.8；单独以区段线路影响最小为优化目标，其最优解为minz3= 50。将3个优化目标值代入评价目标函数中，求解结果如下：其余变量均为0，最优值F= 0.95。通过模型求解结果可知，济南—成都OD的跨线列车最优运行路径为济南—徐州—郑州—西安—广元—成都。

（3）北京—重庆OD跨线列车路径选择。以北京—重庆OD为分析对象，则有o= 1，d= 16。求解得到：单独以列车总运行距离最短为优化目标，其最优解为minz1= 1 825；单独以列车总运行时间最小为优化目标，其最优解为minz2= 456.8；单独以区段线路影响最小为优化目标，其最优解为minz3= 41。将3个优化目标值代入评价目标函数中，求解结果如下：其余变量均为0，最优值F= 12.04。通过模型求解结果可知，北京—重庆OD的跨线列车最优运行路径为北京—保定—石家庄—郑州—武汉—重庆。

3.3 与实际列车开行情况对比分析

从实际跨线列车运行情况来看，太原—南京方向的列车实际选择太原—石家庄—郑州—徐州—蚌埠—南京的运行路径，与计算结果相比较，该运行路径期间只需要跨线1次，并且这一跨线方向并没有换向折返作业的产生，除济南—徐州线路区段外，列车在其他区段均以本线运行的方式通过，因而只需要考虑济南—徐州这一区段线路的影响，并且该路径的总距离最短、总时间最小和区段线路影响能力最小，模型计算的最优路径是合理且具有实际意义的。济南—成都OD方向的列车实际选择济南—徐州—郑州—西安—广元—成都的运行路径，与计算结果相一致，说明该运行路径从距离、时间和区段线路影响程度3方面综合考虑来说，是较为合理的。北京—重庆OD方向的列车实际选择的路径有2条：北京—保定—石家庄—郑州—武汉—重庆和北京—保定—石家庄—郑州—西安—广元—成都—重庆。与计算结果相比较，模型选择的路径通过武汉节点，从京广高速铁路(北京西—广州南)跨入沪汉蓉高速铁路(上海北—成都)，运行期间列车只跨线1次，并没有换向折返技术作业的产生，因而只需考虑武汉—重庆区段线路的影响情况。尽管武汉—重庆区段距离长且设计速度较低，但是从时间、距离和区段线路影响3方面综合考虑，建议北京—重庆方向的列车选择经由武汉的运行路径。

4 结束语

跨线列车运行路径选择是高速铁路列车运行组织设计中的重要环节，也是技术难点所在。针对现有高速铁路路网结构特点及列车跨线作业实际约束要求，运用数学优化方法构建列车运行总距离最短、列车运行总时间最小、区段线路影响最小的多目标优化模型，通过对太原—南京、济南—成都、北京—重庆3条列车OD的实例验证，表明该模型可以有效解决列车选择跨线节点问题，并能够在区段线路通过能力受限条件下，提高列车在路网运行的通达性和高效性。模型生成的跨线列车运行路径方案可作为高速铁路列车运行组织方案编制的参考依据。