微小型移动机器人的路径规划及编队研究

李江昊,闫亚楠,彭 丹

(1.燕山大学 信息科学与工程学院,河北 秦皇岛 066004;2.燕山大学 理学院,河北 秦皇岛 066004)

1 引 言

随着机器人应用的发展和机器人生产线的出现,多机器人系统的研究引起了科研工作者们极大的兴趣[1]。多移动机器人系统是指:多个单机器人形成期望的编队队形[2],来完成某项任务,且可以找到最优路径。因此多移动机器人的路径规划与编队研究成为当前机器人技术的研究热点之一[3]。目前众多的科研工作者们已经对此问题进行了深入的探讨和研究。韩青等[4]提出了一种基于平行导引律的多机器人编队算法。通过虚拟领航者的参考位姿与目标机器人的当前位姿设计出平行导引律,并结合路径规划,设计出基于法向偏差的LQR(线性二次型调节器)轨迹跟踪控制器,该算法在时间表现上更优,但稳定性能欠缺。张大伟等[5]通过针对非完整移动机器人运动学模型的特点,并结合机器人之间的局部交互关系和李雅普诺夫算法,设计出一种具有鲁棒性的编队控制器,该控制器能够有效解决多机器人系统中的对象模型参数不确定的问题,但是没考虑编队中的路径优化问题。易国等[6]提出了一种基于模糊控制的编队算法。根据多移动机器人编队的特点,并结合机器人与障碍物之间的位姿关系,建立了一种机器人编队避障行为的模糊规则,该算法能实现稳定的避障编队,但是无法在编队中实现路径寻优。

本文提出了一种路径寻优与轨迹跟踪相结合的编队算法。首先在传统蚁群算法的基础上,提出一种改进蚁群算法,即改进传统算法的参数和初始信息素矩阵来进行路径规划,使其在收敛性和全局寻优2个方面有了显著提高。然后在规划的路径上进行多机器人编队。为了保证编队的稳定性,本文设计了基于李雅普诺夫算法的轨迹跟踪控制器,仿真实验证明了该控制器误差小、稳定性强。最后在最优路径和轨迹跟踪相结合的基础上,利用领导—跟随法,实现了多机器人的编队任务。

2 改进蚁群算法的研究

2.1 改进蚁群算法的构建

传统蚁群算法存在易陷入局部最优、收敛速度慢、迭代次数多[7],为了提高该算法的收敛速度及全局寻优能力,本文对其进行以下改进:

1) 找到信息素和启发式信息的权重启发参数α、β的最佳范围;当α过小时收敛速度慢,当α过大时,找不到最短路径,α的最佳取值范围为[2,5],同理得β的最佳取值范围为[6,9]。最终选择α=2、β=7作为最优权重启发参数组合。

2) 迭代后期信息素浓度高,易陷入局部最优,改进信息素挥发系数ρ。ρ取值对算法性能的影响如表1所示。

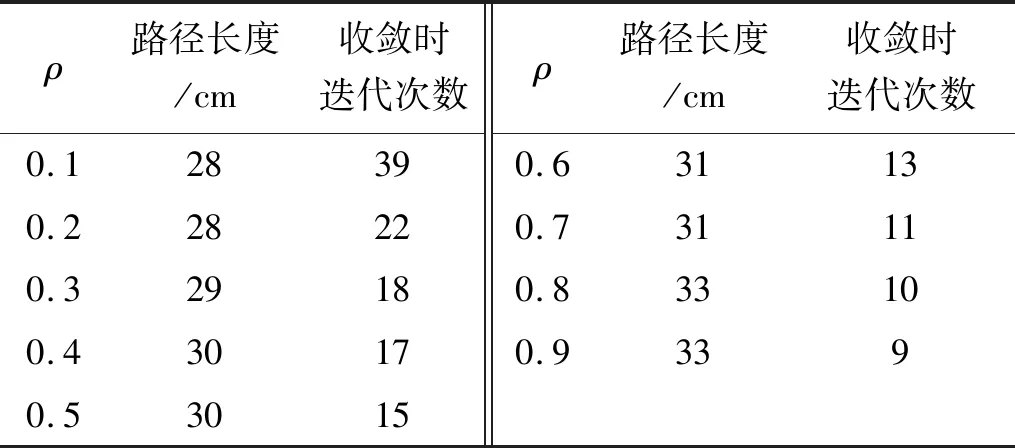
表1 ρ取值对算法性能的影响Tab.1 Algorithm performance impact on ρ

该算法中其他参数取值为:K=100表示迭代总次数,Q=1表示信息素增强系数,M=50表示每次迭代的蚂蚁总数,α=2表示信息素的启发因子,β=7表示启发式信息的启发因子。

当挥发系数ρ过大时,信息素积累速度慢,该算法全局搜索能力降低;当ρ过小时,信息素累积过多,扰乱蚂蚁选择,收敛速度降低。因此为了增加其收敛速度和全局寻优能力,本文将ρ设计成以迭代次数k为自变量的函数。由表1可知:ρ的最佳取值范围为[0.2～0.5],分析ρ的变化规律,可推算出ρ的函数表达式ρ(k)为:

(1)

式中:k为当前迭代次数;ρ(k)为当前迭代次数下的信息素取值。

为了验证函数ρ(k)和ρ常值对于蚁群算法性能的影响,通过20次仿真得到表2所示结果。

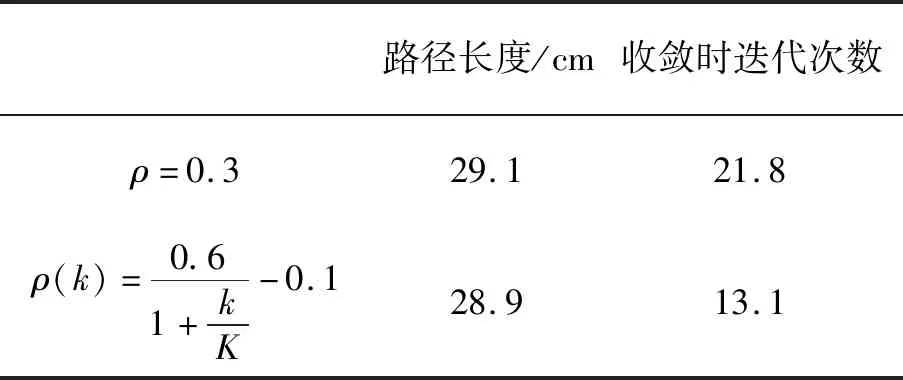
表2 ρ函数与ρ常值对算法性能的影响Tab.2 Algorithm performance impact on function ρ and Constant ρ

通过表2可知:ρ=0.3和ρ(k)对该算法在平均路径性能上差别不大,因为实验次数有限,故最优路径存在一定的差距可以接受。但两者在平均迭代次数上存在较大差距,显然ρ(k)时的收敛速度明显比ρ=0.3时的收敛速度快。

3) 初始信息素匮乏,收敛速度慢[8],根据启发式信息,寻找初始信息素分布,提高收敛速度。

改进思路是:在蚁巢和食物源间,理论上最短距离是两点间直线距离,此直线称为“中心直线”,即“中心直线”所在栅格上信息素浓度最大,“中心直线”所经过的栅格称“中心栅格”,在实际觅食中,会存在各种障碍物使蚂蚁不能直线通过,必须在绕开障碍物的同时选择一条最优路径,因此离“中心直线”距离越近的栅格上的信息素就越多的。

针对初始化信息素分布给如下计算方法:

1) 计算每个栅格到所有“中心栅格”的距离,两栅格间距离越小,说明该栅格离“中心栅格”的位置越近,故该栅格上信息素浓度越大,反之浓度越小。

2) 已知每个栅格上的信息素浓度,计算经过两个栅格间路径上的信息素浓度,假如蚂蚁在栅格处,下一步走到栅格j处,则路径(i,j)上的信息素浓度与两个栅格信息素浓度之和成正比,由此求得的信息素矩阵称为“栅格信息素矩阵”。

3) 障碍物所在栅格上信息素为零,且若栅格和栅格j不相邻,则路径(i,j)上的信息素浓度也为零,对此将2)中的“栅格信息素矩阵”,与邻接矩阵相乘可得初始信息素矩阵。

表3 改进初始信息素对算法性能的影响Tab.3 Algorithm performance impact on improved initial pheromone

由表3可知:改进初始信息素后的算法相较于传统算法在路径寻优和收敛速度方面都有提高。

2.2 改进蚁群算法仿真及对比分析

采用栅格法进行建模,能够方便处理障碍物边界问题[9]。本文所构建的机器人栅格地图空间为20 cm×20 cm,栅格边长为1 cm,其中黑色代表障碍物,白色代表自由空间,由于本文研究的机器人是微小型机器人,即障碍物远远大于机器人,因此机器人在栅格间的移动可近似成一个质点。

传统算法收敛曲线和最优路径图如图1所示。改进算法的收敛曲线和最优路径图如图2所示。

图1 传统蚁群仿真图Fig.1 Traditional ant colony simulation

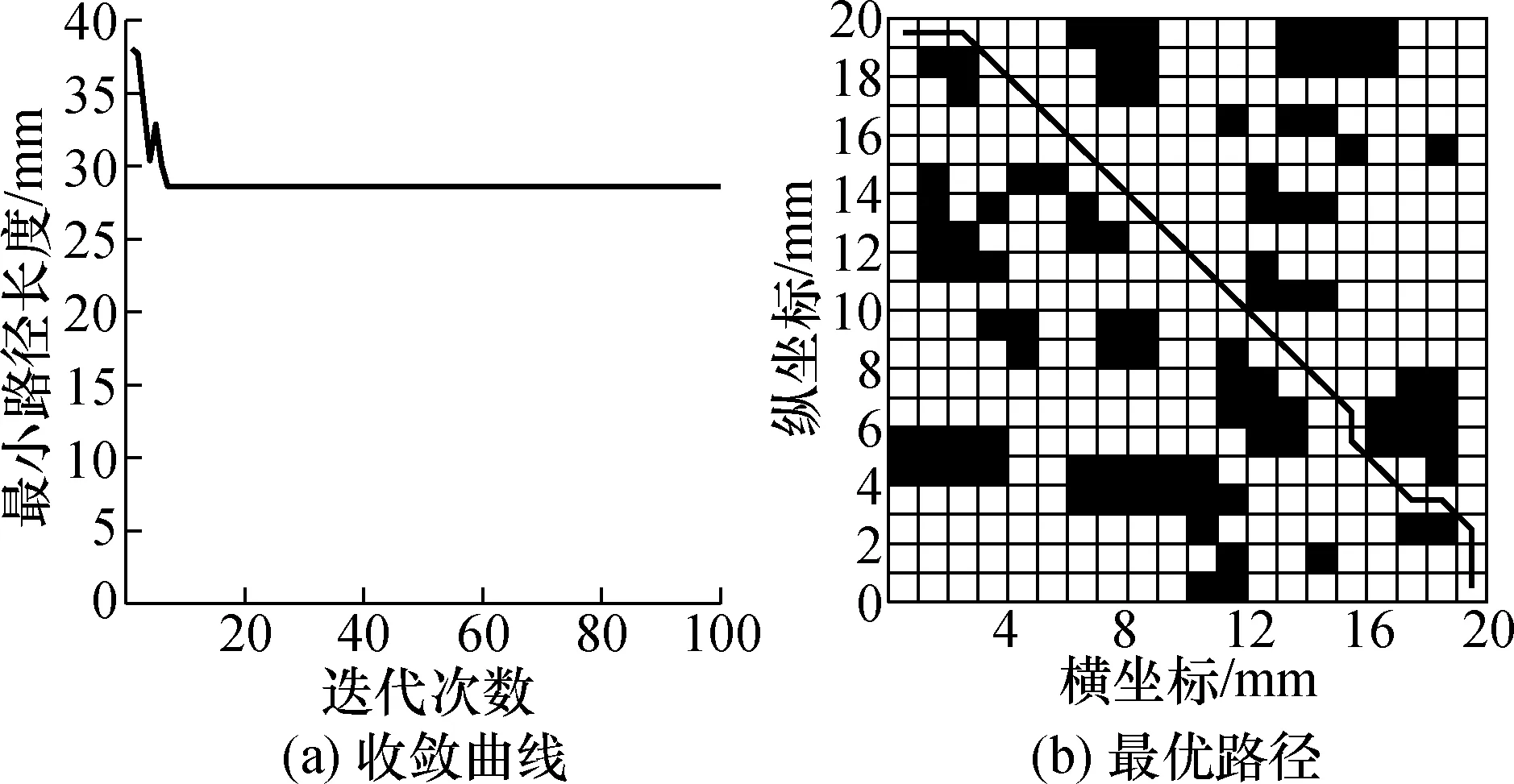
图2 改进蚁群仿真图Fig.2 Improved ant colony simulation

由图1和图2可知:改进算法收敛时的迭代次数为8次,传统算法为15次,且两者最短路径都为28 cm。但在20次仿真中,达到最短路径的次数传统算法6次、改进算法12次,改进算法全局寻优能力提高了30%。由2种算法平均迭代次数可知,改进算法收敛速度提高了50%。由此可见,改进算法相较于传统算法在收敛速度和全局寻优能力2个方面都有显著提高。

3 轨迹跟踪控制器的设计

3.1 李雅普诺夫稳定性分析

评判一个系统的标准需首先证明该系统是稳定的,而通过机器人运动误差构造李雅普诺夫函数便可判断动力系统的稳定性[10]。本文利用李雅普诺夫直接法结合反推法寻找合适的轨迹跟踪控制律[11]。

定义李雅普诺夫函数为:

(2)

式中:k>0,V≥0,当且仅当xe=ye=θe=0时,V=0。对式(2)进行求导得:

(3)

在全局坐标系下,机器人的运动学方程为:

此时,利用Kaczmarz迭代算法循环遍历矩阵U的所有行,并将当前迭代Ui投影至与矩阵V中当前选择列所对应的超平面上,即可求解子优化问题式(8).与之类似,利用Kaczmarz迭代算法循环遍历矩阵V的所有列,并将当前迭代Vj投影至与矩阵U中当前选择行所对应的超平面上,即可求解子优化问题式(9).本文通过循环交替求解子凸优化问题式(8)和式(9),即可由观测矩阵Y的部分已知元素重构感知矩阵X的所有未知元素.

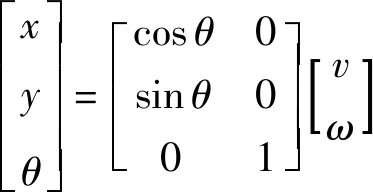
(4)

机器人位姿误差微分方程为:

(5)

将式(5)代入式(3)得:

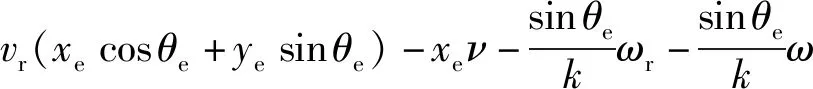
(6)

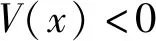
(7)

式中:k1>0,k2>0将式(7)代入式(6)得

(8)

3.2 系统仿真及分析

图3所示为基于PID算法的8字形轨迹跟踪仿真图。图4所示为基于李雅普诺夫算法的8字形轨迹跟踪仿真图。由图的仿真结果可知:PID控制器和李雅普控制器都能实现8字形轨迹跟踪。在PID控制器中,x轴方向的误差稳定在[-1.16 m,1.16 m],y轴方向的误差稳定在[-0.3 m,0.3 m];而在李雅普控制器中,x轴和y轴方向的误差最终都趋于0。可见,李雅普控制器在轨迹跟踪中误差更小,稳定性更强。因此选用基于李雅普诺夫算法的控制器进行机器人的圆形轨迹跟踪。

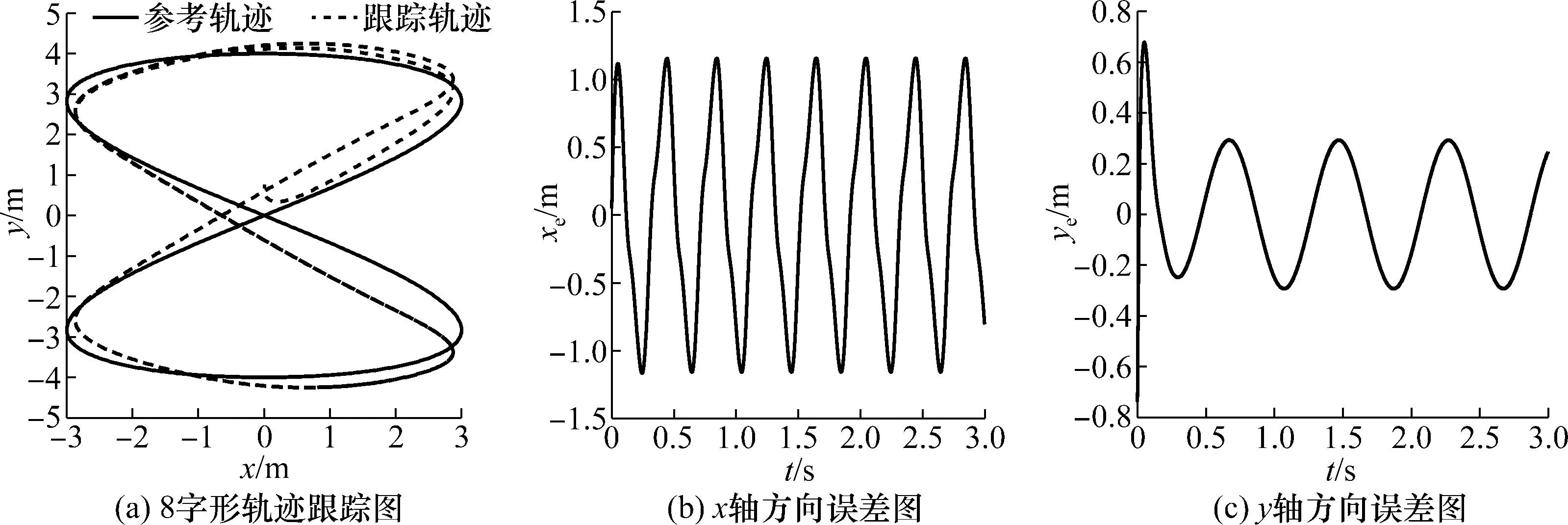
图3 基于PID控制器的8字形轨迹跟踪仿真图Fig.3 8-bit trajectory tracking simulation based on PID controller

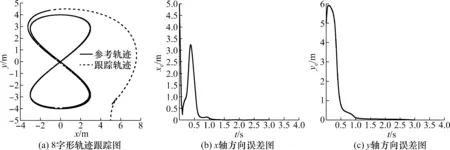
图4 基于李雅普控制器的8字形轨迹跟踪仿真图Fig.4 Simulation diagram of 8-shaped trajectory tracking based on Lyapu controller

当轨迹跟踪控制率如式(7),且其中参数如表4所示时,得到的机器人轨迹跟踪图,如图5所示。

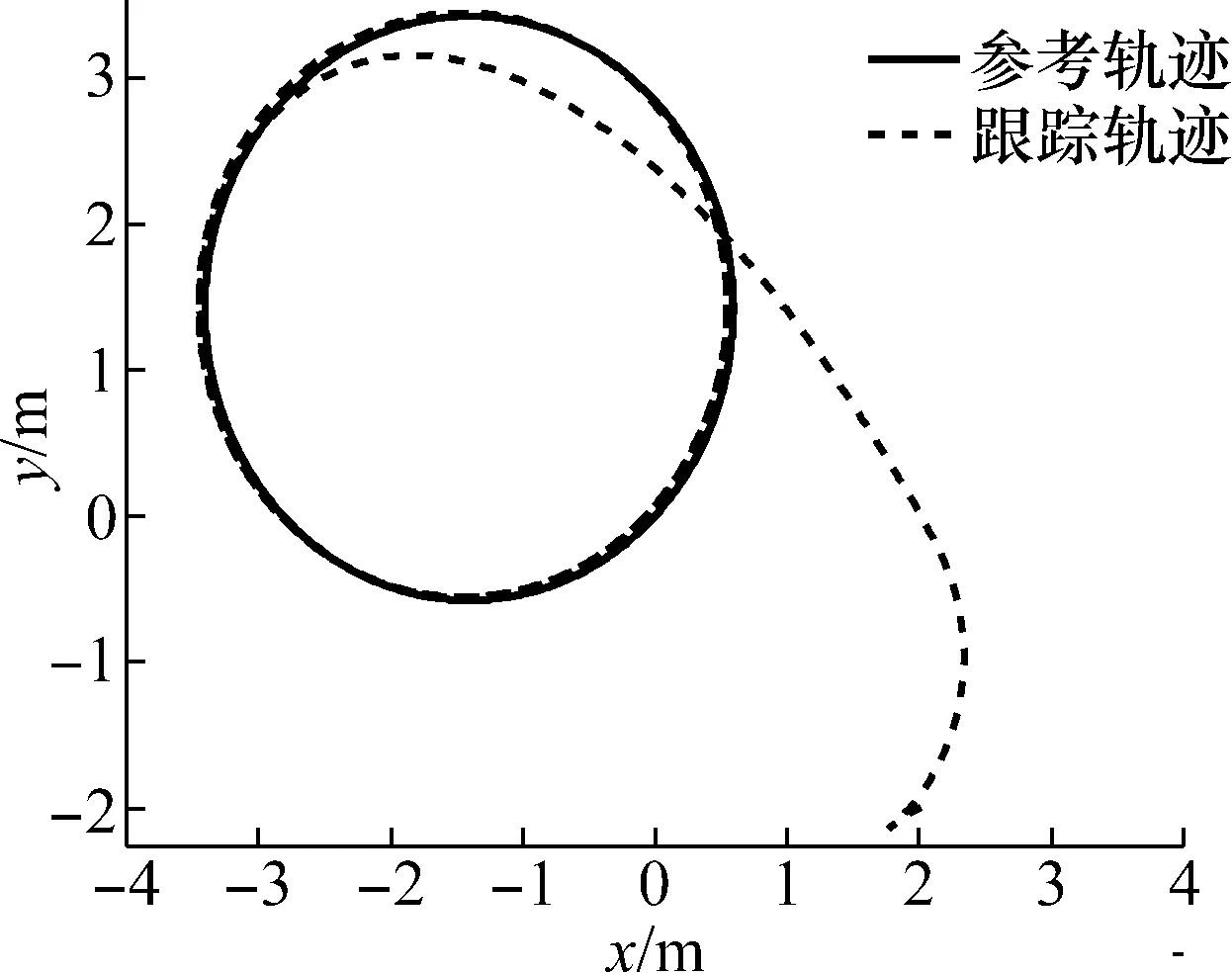
图5 机器人圆形轨迹跟踪图Fig.5 Robot circular trajectory tracking diagram

表4 李雅普诺夫控制器仿真参数设置Tab.4 Lyapunov controller simulation parameter settings

图6所示为李雅普控制器的圆形轨迹跟踪图,图7所示为控制率变化图。由仿真结果可知,基于李雅普诺夫算法的轨迹跟踪控制器可以实现机器人的轨迹跟踪,且在跟踪过程误差更小、稳定性更好。

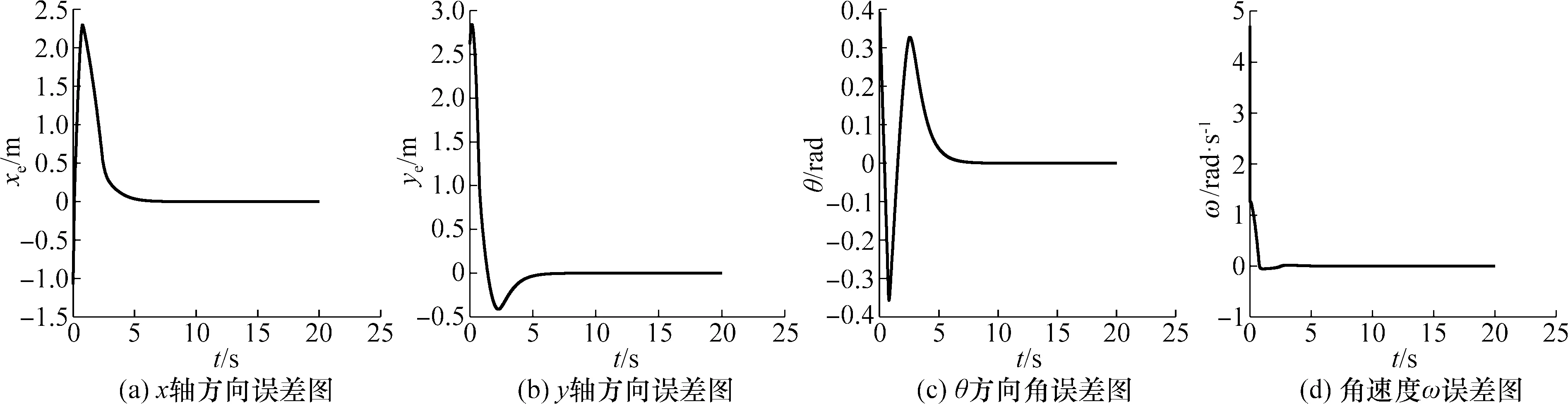
图6 机器人圆形轨迹误差仿真图Fig.6 Robot circular trajectory error simulation

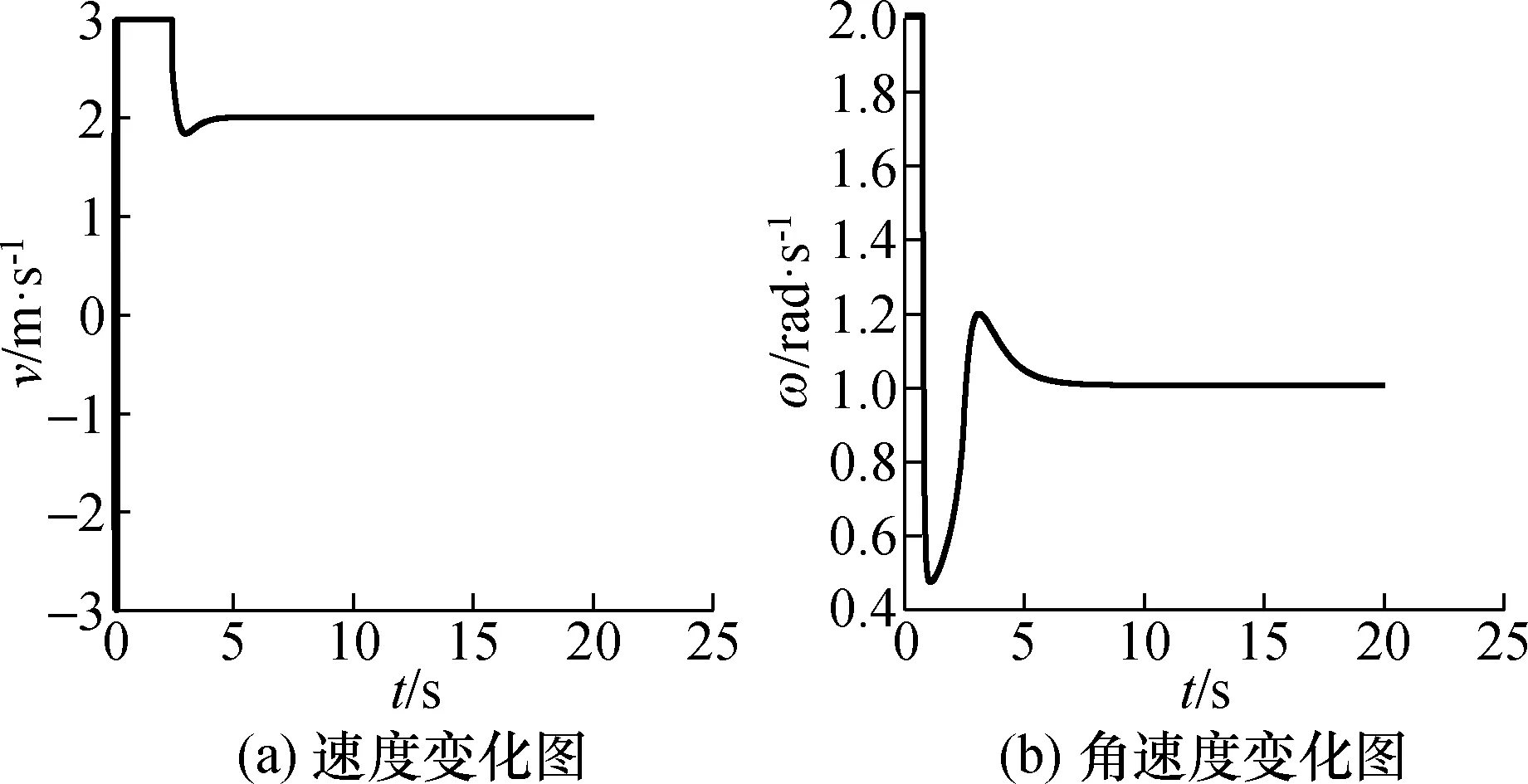
图7 圆形轨迹控制率变化图Fig.7 Circular trajectory control rate change diagram

4 多移动机器人的编队控制

4.1 编队控制器的设计

本文选领航-跟随法进行多机器人编队,该方法易实现,发展成熟。在领航-跟随法中,若领航者发生故障,整个编队系统将会面临瘫痪,无法完成编队任务。因此本文将已知参考轨迹赋给编队队形质心,其它机器人只需要与该质心保持相应的距离和角度即可,且任一机器人发生故障,均不影响整个编队系统,此编队控制方法如图8所示。

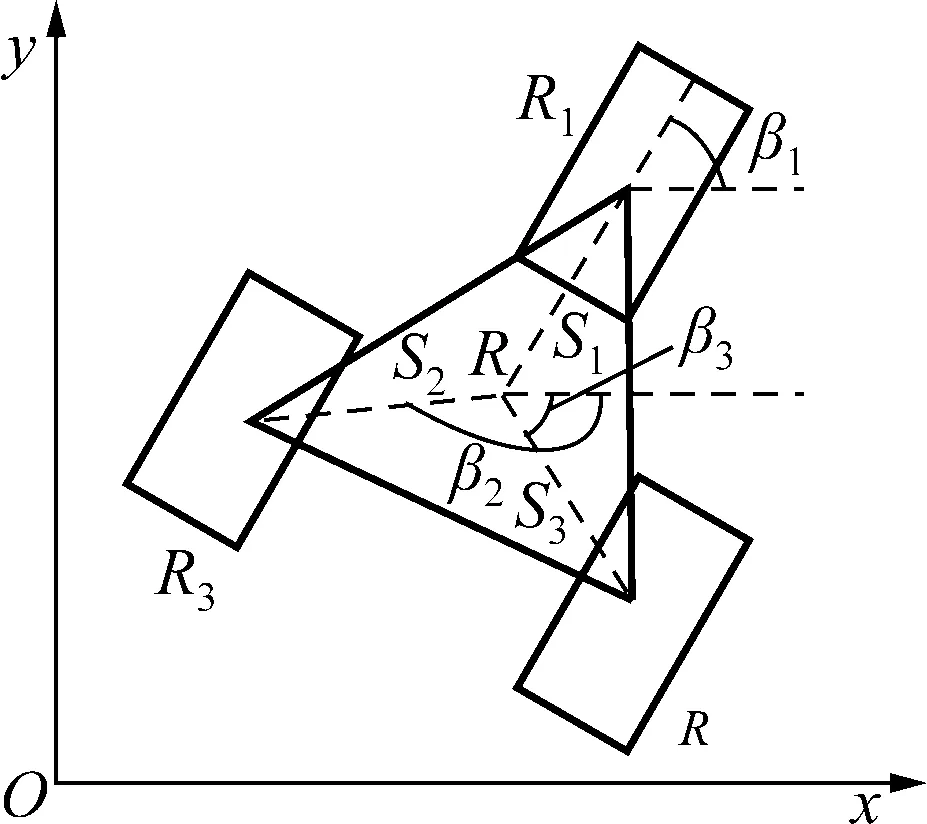
图8 编队队形示意图Fig.8 Schematic diagram of formation formation

如图8所示,3个机器人分别为R1、R2、R3组成三角队形,其中R为质心坐标,且每个机器人都满足式(4)所示的运动学方程。已知质心参考轨迹,期望编队队形可通过设置每个机器人到质心的参数(如距离参数Si和角度参数βi)来得到每个机器人的参考轨迹。已知质心轨迹为R(xr(t),yr(t)),机器人Ri的参考轨迹可定义为:

(9)

在多机器人编队中,若每个机器人都跟踪自己的参考轨迹,就可实现多机器人的稳定编队。由此便将多机器人的编队问题转化成轨迹跟踪问题,降低了编队问题的复杂度[12],简化了计算。

4.2 多机器人编队仿真与分析

1) 本文主要分析3个机器人进行等边三角形编队的情况,当多机器人的质心轨迹是沿着直线运动时,其仿真结果如图9所示。

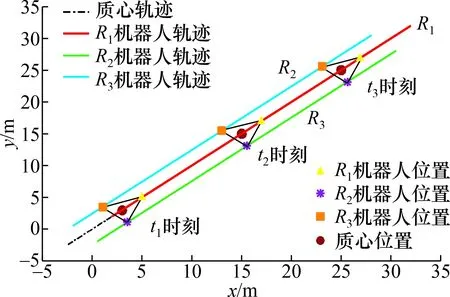
图9 多机器人直线编队轨迹图Fig.9 Multi-robot line formation trajectory

假设机器人的质心轨迹为:

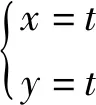
(10)

距离参数S1=S2=S3=2 m,若β1= π /4,则机器人R1、R2、R3的参考轨迹为:

(11)

(12)

(13)

2) 当多机器人质心轨迹为圆形轨迹,其仿真结果如图10所示。

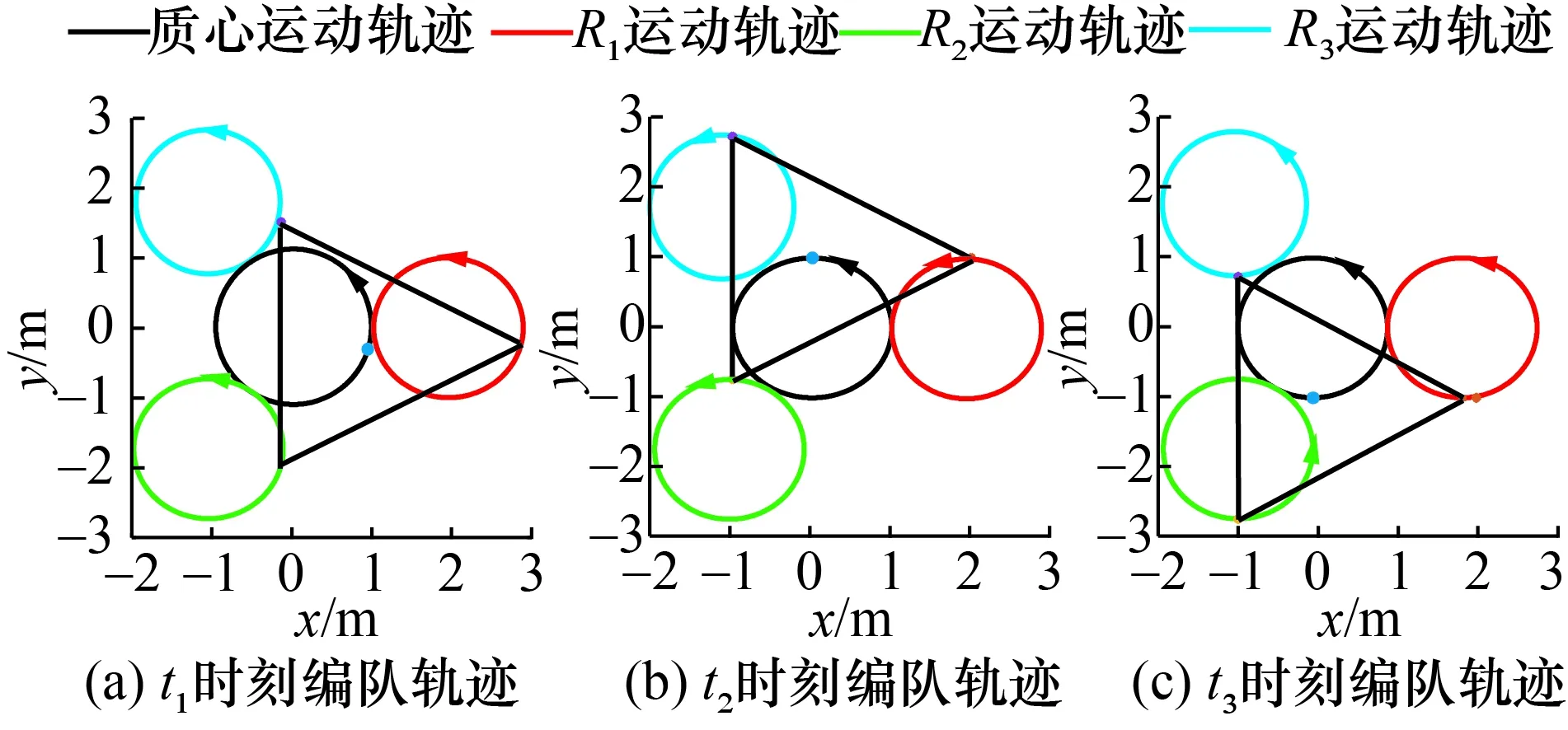
图10 多机器人圆形编队轨迹图Fig.10 Multi-robot circular formation trajectory

假设移动机器人质心的轨迹为:

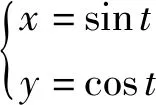
(14)

距离参数S1=S2=S3=2 m,若β1=0,则机器人R1、R2、R3的参考轨迹分别为:

(15)

(16)

(17)

通过仿真分析发现,在多机器人系统编队中,当质心轨迹沿逆时针方向行驶时,机器人也沿逆时针方向行进。由图10可知机器人在编队过程中一直保持着三角队形的稳定编队。

5 结 论

本文提出了基于路径寻优和轨迹跟踪的编队方式。相比于文献[4],本文提出的李雅普诺夫控制器增强了编队的稳定性;相比于文献[5],本文利用改进蚁群算法找到的最优路径提高了编队的速度。更深一步的研究任务是多移动机器人的动态路径规划和进行多机器人编队的队形变换。