梁格法在城市桥梁设计中的应用研究
2021-06-04董营,刘松
董 营,刘 松
1.山东省路桥集团有限公司,山东 济南 250014
2.济南市市政工程设计研究院(集团)有限责任公司,山东 济南 250003
近些年,柔性桥、箱梁桥等结构形式陆续出现,为确保其施工与使用过程的安全性,为城市经济发展做出更大贡献,相关部门应分析其结构的空间内力分布与变形情况。其中,梁单元法、板壳元法及梁格法等均是常用方法。相比之下,梁格法的计算成本相对较低、能较快捷地提取计算结果且还能和现行桥梁建设规范相匹配,目前梁格法在桥梁工程分析领域有较广泛的应用。文章基于梁格法的基本原理,参照现实案例,归纳梁格法在城市桥梁设计中的应用情况。
1 梁格法的基本原理
梁格法是利用一个等效的梁格将桥梁上部结构取而代之,可以将其看成是一种将梁作为基本单元的有限元法。该方法在应用阶段表现出概念明确化、便于理解与操作使用、测算较快速等特点。目前国内现有的计算曲线梁桥的软件,如《桥梁博士》等,均应用了梁格法。
梁格法用于工程领域的主要思路是用一个等效的平面梁格或者空间构架去仿真模拟上部结构,把分散于板式或箱梁各个区段中的弯曲及抗扭刚度聚集在相毗邻的等效梁格中,真实结构的纵向、横向刚度则分别被集中在纵向、横向梁格构件中。通过分析该平面梁格或空间构架,能够较顺利地获得实体桥梁上部结构纵、横向内力分布与变形状况。对于箱形截面而言,如果把腹板设定为基本单位划分梁格,则据此便能够获得腹板的真实受力特征,可以直接利用其计算出腹板的配筋,借此方式规避既往用空间梁元与空间箱形梁元分析阶段务必横向配置各个腹板内力的流程,使工程设计工作更简单、快速地推进。梁格法在应用阶段的关键点在于其和桥梁上部结构形成了等效性,等同于在相等荷载作用下维持两者内力分布与变形状态一致,这就预示着是否能达到等效性直接影响结构分析结果的准确度。
2 梁格法单元划分及截面计算
2.1 梁格单元划分
整体而言,一定要参照桥梁上部结构与支座状况,并结合结构力学有关原理及既往形成的工程施工经验进行梁格划分,梁格划分应遵循的常规规则如下。
(1)尽可能使梁格和设计受力线相互重合。例如,和预应力或梁构件成角180°,顺沿边梁及支座上的受力线等进行操作,借此方式实现对桥梁结构作业状态的有效模拟。
(2)尽量使梁格符合原型结构内力分布状态。比如,在板桥梁格对应的等效模型内,明确要求各根边缘梁格一定要临近上部结构边界位置并和剪力流的合力相互垂直。
(3)尽可能使梁格横、纵向构件间距值接近,借此方式增加梁格结构对荷载的静力分布状态的灵敏度。
(4)划分平面梁格模型时,尽量使各部分的形心轴与整体的形心轴方位等同。
2.2 梁格截面计算
加载具体方位与不同单元之间的相对刚度是梁格法配置荷载的主要依据,构件截面特性是影响刚度值高低的主要因素之一,故而准确测算出梁格单元的截面特性能使最后测算结果的精确度得到更大保障。
就板式上部结构而言,可以依照正交各向同性板测算出钢筋砼及预应力砼实体板桥,参照以下公式测算出截面特性:

式中:i、c分别为单位板宽构件的惯性矩和有效抗扭常数;h为板的厚度。
对于箱梁而言,通常会把纵向构件细化成数个工字梁,纵向单元特性测算过程较为简单,其实便是采用相对应的工字梁面积、抗弯惯性矩以及腹板横截面面积分别表示纵向单元面积、抗弯惯性矩、抗剪面积。可以将横向单元看成是由上下两块板共同构成的空腹断面,于荷载作用下统一环绕它们的共同重心水平中性轴弯曲。横向梁格面积等于其所代表范畴中顶底板的面积总和,可以利用以下公式计算出惯性矩按绕板的共同重心:

式中:d'、d〃、h'、h〃为板的厚度及各板至其形心的距离值。
当箱梁结构进行整体扭转时,大部分的剪力流环绕顶板、底板与腹板的周界进行流动,仅有极少部分会流经中间腹板。解读剪力柔性梁格相关理论,在顶板与底板内的相逆剪力流共同作用下形成了上部结构中的扭矩,顶板与底板是提供抗扭刚度的主体构造,可以采用以下公式测算出单位纵向或横向梁格构件的抗扭常数:

3 工程应用案例
现有一座双跨连续钢筋砼实心板桥,桥面宽为12.9m、长为40m,主体桥面宽度×高度为8m×1m,两侧翼缘宽,高度分别为2.4m、0.4m。桥梁工程建设阶段所用的砼材料基本参数如下:密度为2600㎏/m³,弹性模量为35GPa,泊松比为0.168。利用梁格法测算其结构受力特征,并且和实物体有限元计算结果进行比较分析。参照梁格法形成的理论,先划分梁格与测算出单元刚度等效数值,划分梁格期间为了确保最后测算结果的精确性,该工程依照横向1m宽度进行分析,两侧2.4m的翼缘均依照1.2m梁格规格确定,纵向尺寸为1m。梁格的具体划分情况如图1所示,参照划分出的梁格单元测算出其对应的等效刚度。在以上过程中应关注因左右两侧翼缘的高度存在差异而造成其截面形心方位和主体界面存在一定不同这一现实情况,并且具体测算阶段应考虑对梁格2~3以及10~11安设横向刚性衔接,借此方式使两者受力状态与变形程度的统一性得到更大保障。

图1 梁格划分图示
应用梁格法与实体有限元方法测算出自体重量作用下沿着桥向梁体的弯矩结果,如表1所示。通过比较分析不难发现,梁格法下的计算结果和实体有限元计算结果两者的吻合度相对较高,误差基本被控制在6.0%以下,不管是对整体的弯矩状况或者是对特殊构件3的弯矩配置,均较好地证实了梁格法计算结果的准确性,在城市桥梁设计计算领域有较高的适用性。
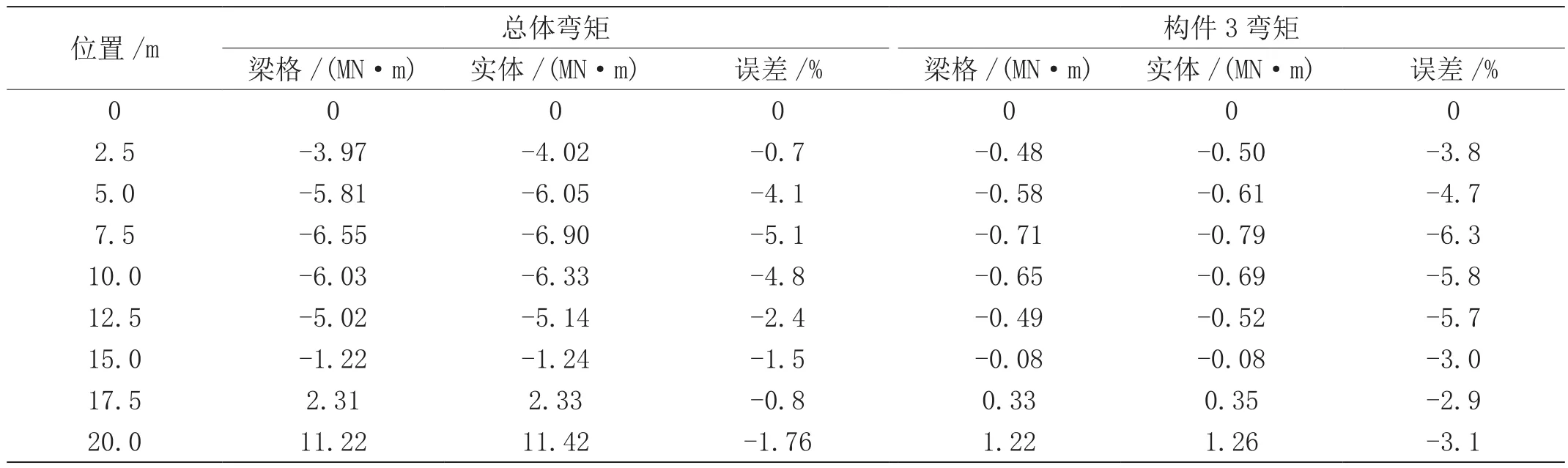
表1 梁格法的计算结果和实体有限元计算结果比较
4 结束语
梁格法是当下桥梁工程建设阶段分析桥梁结构空间的一种常用方法,其在应用阶段能取得较理想的结果。梁格法有概念清楚明确、便于理解与操作使用等诸多特征,在城市桥梁的宽梁桥、斜交桥等多种结构型式中表现出了较高的适用性。文章在分析梁格法基础理论的基础上,解读了梁格划分与刚度计算两个主要问题,利用实际工程案例对梁格法的计算结果和实体有限元计算结果进行了比较分析,两者形成的误差被控制在6.0%以下,说明梁格法的精确度较高,在桥梁工程结构分析中有较高的推广价值。
