站桥合一式复杂结构的动力特性及抗震分析

陈 雷， 陈远久， 贾继祥

(西南交通大学桥梁工程系，四川成都610031)

钢-混组合结构兼具钢结构和混凝土结构的优点，经济效益和社会效益显著，因而在我国得到了广泛的应用[1]。站桥合一作为一种新近发展起来的结构，可以最大化地发挥城市空间利用率，提高城市交通运营效率[2]。其主要受力结构常采用钢-混组合结构，虽在工程实践中已有了部分应用，但截止到目前对其系统理论研究仍略显不足，研究成果并不丰富[3-6]。本文以某站桥合一式的综合交通枢纽为依托，采用桥梁空间有限元计算分析软件Midas/Civil分析其动力特性和地震响应，为站桥合一技术的实际运用提供有益的参考。

1 工程概况

某站桥合一式的结构位于城市主干道上，为3条地铁线路的换乘枢纽，客流量巨大。车站采用地下三层多跨框架式结构，车站主体长120 m，宽96 m，为了满足建筑功能和景观需求，中庭部分50 m×48 m范围内无支撑柱。中庭大跨区域纵横向主梁采用矩形钢管混凝土结构，支撑柱采用圆形钢管混凝土结构，车站边跨小跨度区域纵横向主梁采用矩形钢筋混凝土结构，支撑柱采用圆形钢筋混凝土结构。查阅相关文献可知目前国内的中庭大跨最大跨径为24 m，此项目中的中庭大跨的跨径之大实属罕见。中庭大跨及其附属部分结构平面示意图如图1所示。

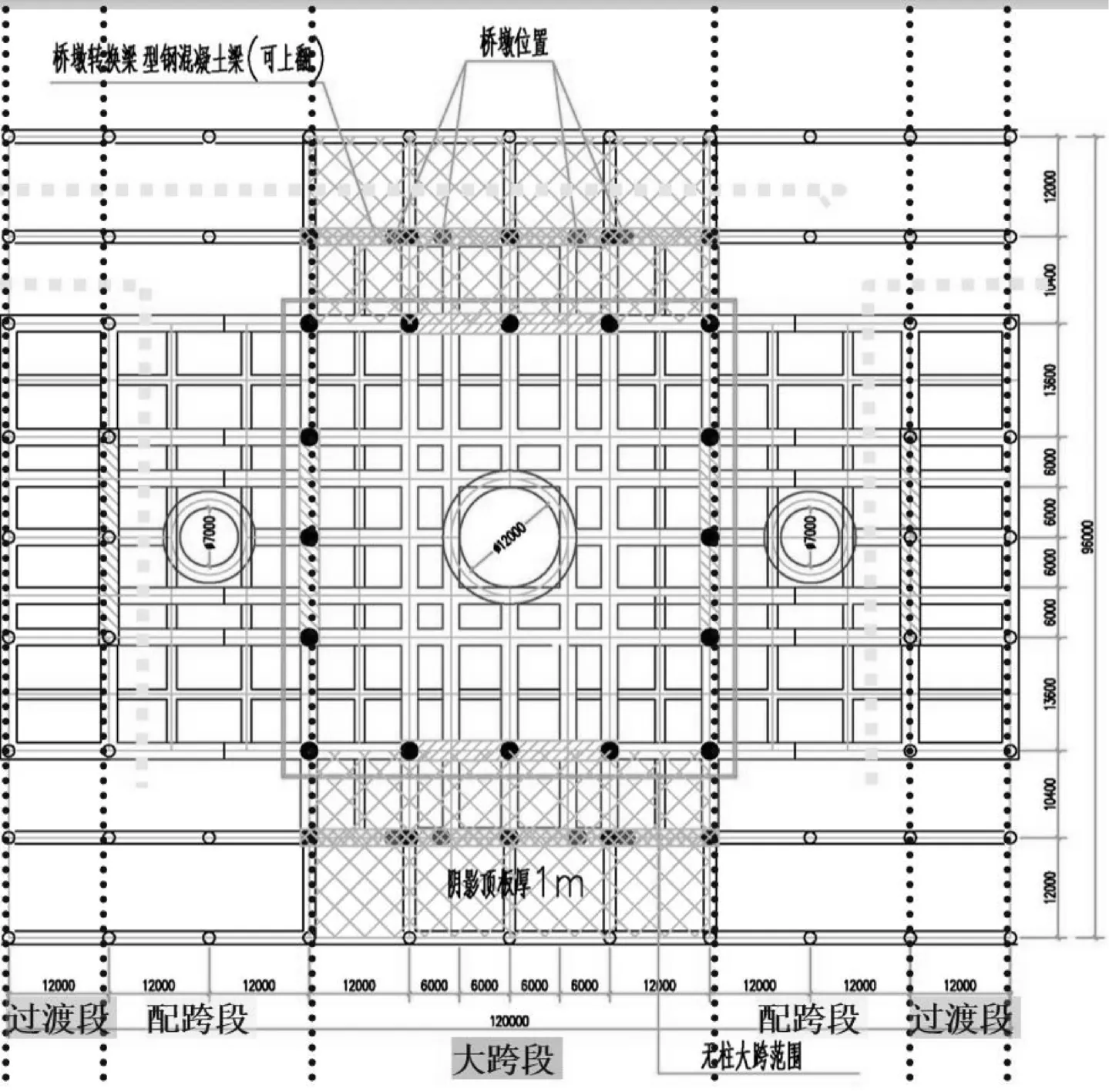
图1 中庭大跨及其附属部分结构平面示意(单位:mm)

地铁车站上方布置一座跨径为(50+80+50) m三跨连续钢箱梁桥，钢箱梁桥为南北走向，其中80 m主跨位于车站正上方。桥梁结构采用双柱式混凝土墩，主跨的两桥墩与车站的转换梁固结，形成复杂的站桥合一式结构体系，如图2所示。该结构的动力特性对结构性能的影响尤为关键，通过分析其动力特性可以为结构的抗震分析提供必要的基础数据和理论支撑。

图2 站桥合一式结构

2 有限元计算模型

采用桥梁有限元分析软件Midas/Civil建立站桥合一结构空间有限元计算模型，如图3所示。地铁车站结构柱和纵横梁采用梁单元模拟，三层楼板采用板单元模拟，整个结构共划分2 565个单元。桩基础端部按固结处理，桥墩和主梁采用弹性连接。三跨连续钢箱梁采用Q345钢材，桥墩采用C40混凝土，地铁车站钢结构采用Q420钢材，混凝土采用C60混凝土，相关的材料参数见表1。

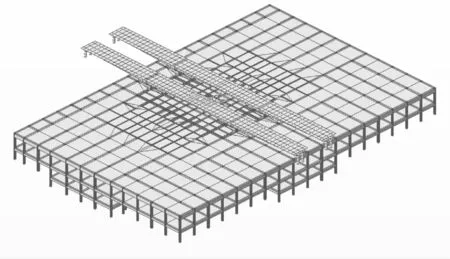
图3 站桥合一结构有限元模型

表1 材料参数

3 结构动力特性分析

采用多重Ritz向量法对该站桥合一结构进行特征值分析，通过计算得到了结构的前30阶模态，确保站桥合一结构在三个方向上的振型参与质量均满足大于90 %的要求。其中前5阶振型及自振频率如表2所示，前5阶自振模态如图4所示。

表2 站桥合一结构自振频率、周期及振型特征

图4 整体结构前五阶振动模态

由上述图表可知：

(1)站桥合一结构基频为1.312 4 Hz，周期为0.762 0 s。前五阶振动模态均表现为地铁车站的边跨振动，边跨振动幅度较大，中跨振动幅度较小。说明站桥合一结构的动力特性主要由地铁车站控制，边跨振动较大是因为边跨混凝土梁横向连接较弱，为改善边跨的动力特性，实际工程中可适当在边跨增设横梁，增强边跨混凝土梁的横向刚度。

(2)受到地铁车站的影响，站桥合一结构中钢箱梁桥的基频为1.363 9 Hz，周期为0.733 2 s，第1阶振型是顺桥向纵飘。说明地铁上方桥梁的振动模态随地铁车站的振动模态发生相应改变，站桥合一结构的动力特性由地铁车站控制。

4 单独钢箱梁桥动力特性分析

为研究站桥合一结构和单独钢箱梁桥结构动力特性的区别，重新建立钢箱梁桥模型并分析其动力特性，根据两者的动力特性结果判别站桥合一结构中地铁车站对桥梁的影响。采用多重Ritz向量法求解结构的前30阶模态，取其前5阶自振特性如表3所示，前5阶振型图如图5所示。

由上述图表可知：

(1)单独钢箱梁桥基频为1.585 0 Hz，周期为0.630 9 s。

表3 单独钢箱梁桥自振频率、周期及振型特征

单独钢箱梁桥钢箱梁桥前两阶振型特征是竖向挠曲，第3阶振型出现纵飘，第4阶振型出现横弯；而站桥合一结构中钢箱梁桥的基频为1.368 9 Hz，周期为0.730 5 s，第1阶振型是顺桥向纵飘。说明与下部车站合建之后，受到地铁车站的影响钢箱梁桥的基频变小。

(2)对比站桥合一结构和单独钢箱梁桥的前5阶振型，站桥合一结构的前5阶振型主要是下部车站的横向和纵向的变形，钢箱梁桥未出现竖向变形，而单独钢箱梁桥模型第1阶振型为竖向正对称挠曲，说明与下部车站合建之后，钢箱梁桥的横桥向和纵桥向刚度均变小。

(3)站桥合一结构的基频小于单独钢箱梁桥的基频，而且前5阶振型中站桥合一结构的基频均小于单独钢箱梁桥的频率，说明站桥合一结构的动力特性由地铁车站控制。

图5 模型前5阶振型

5 站桥合一结构时程分析

5.1 地震波的选取

现有工程结构的抗震分析方法有反应谱法和时程分析法，时程分析法属于瞬态动力学分析方法，可以计算在地震荷载激励下结构的位移、应力随着时间变化的关系[7]。本文采用时程分析法(线型)分析站桥合一结构的地震响应。该结构抗震设防类别为B类，分区特征周期Tg=0.35S，场地类型为Ⅱ类，抗震设防烈度为7(0.1g)，对EL-Centro_t波进行修正并作为地震动输入。修正后的地震波如图6所示。

图6 修正EL-Centro_t波

本文采用纵向、横向、纵向+竖向、横向+竖向、纵向+横向+竖向五种工况来分析站桥合一结构中钢箱梁桥主梁控制截面内力。为了便于叙述取钢箱梁桥支座处与跨中处14个梁截面进行编号，如图7所示。

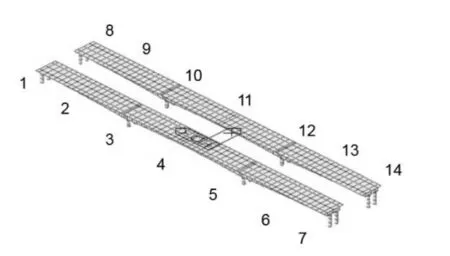
图7 支座与跨中控制截面编号

5.2 时程分析结果

采用Midas/Civil有限元软件进行时程分析后，得到五种工况下的主梁控制截面受力情况，限于篇幅原因，截取1～7号主梁控制截面的内力表如表4～表6所示。

为了便于分析结果，将纵向+横向+竖向三维地震波一致激励工况的内力数值结果作为基准值，得到各工况下控制截面轴力、弯矩的比值，并绘制点线图，如图8、图9所示。

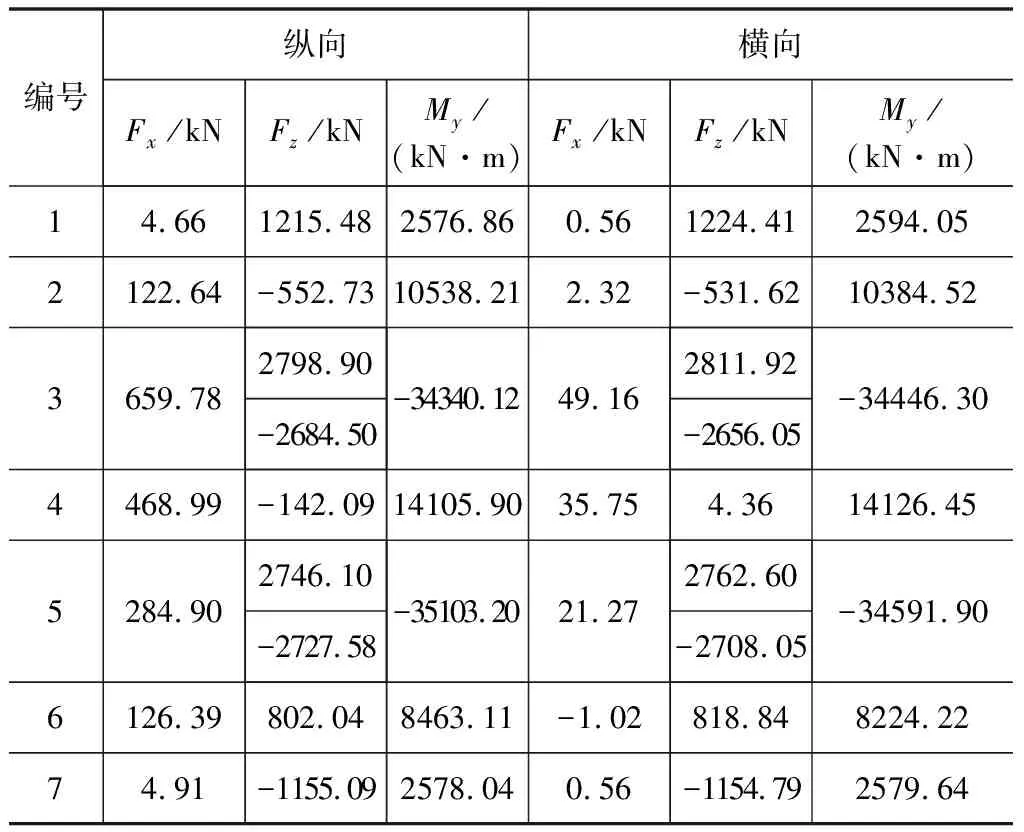
表4 不同工况下主梁控制截面内力

表5 不同工况下主梁控制截面内力

图8 各工况下主梁控制截面轴压力比值

表6 不同工况下主梁控制截面内力

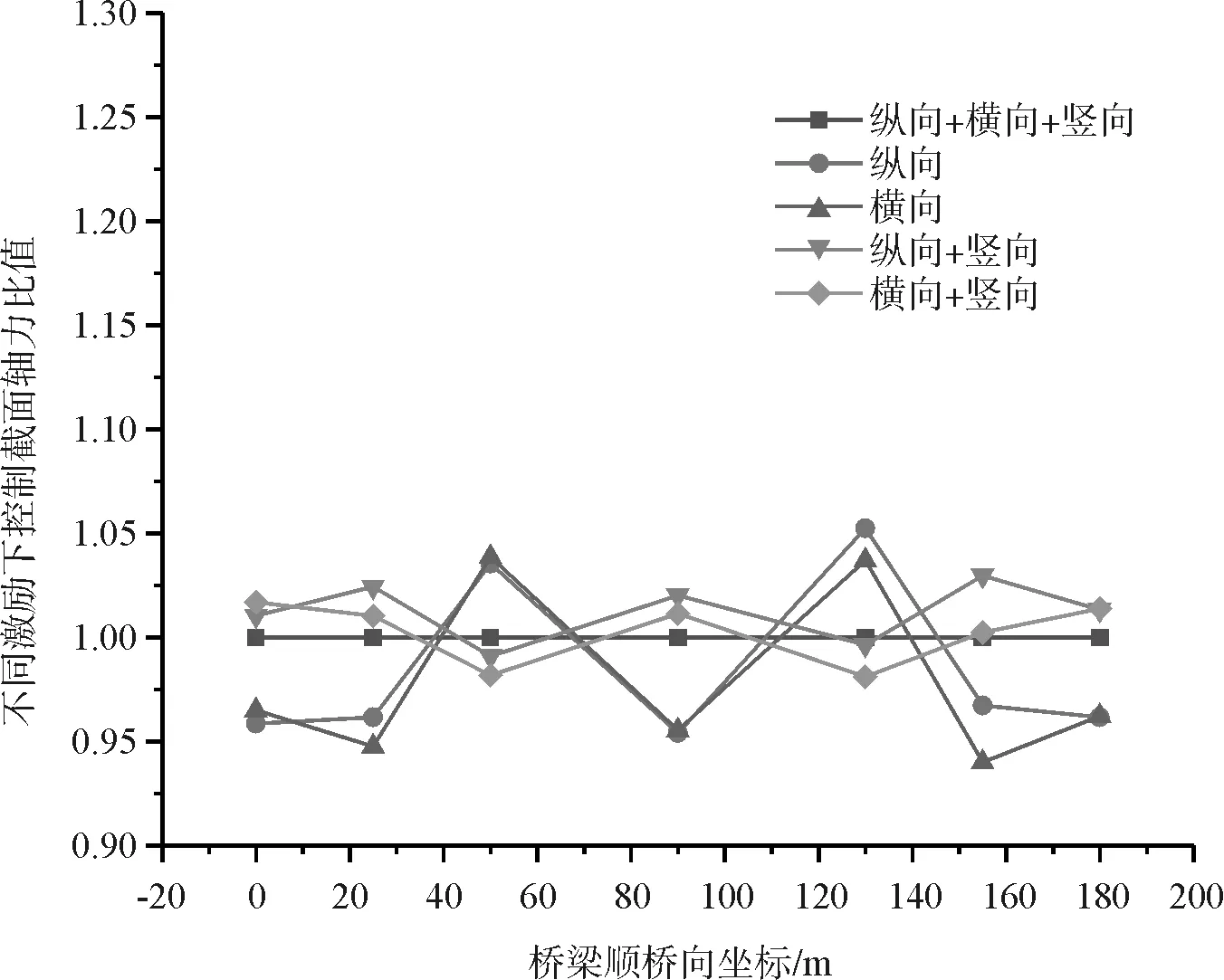
图9 各工况下主梁控制截面弯矩比值

综合上述5个工况下的时程分析结果可以得到以下结论：

(1)不同方向地震激励下，最大轴力、最大弯矩均出现在跨中支座处3号截面，为桥梁抗震设计中承载力的控制截面。

(2)分析主梁控制截面的轴力时，纵向+竖向工况下的轴力最大，纵向地震波对主梁控制截面的轴力影响较大，表现为纵向地震水平力对主梁轴力的参与效应，与结构动力学理论相吻合。

(3)在纵向工况和横向工况等一维激励作用下，相对于三维激励作用，主梁跨中支座处3号截面和5号截面的负弯矩均有所增大，但增加幅度仅为5 %。

(4)最大正弯矩在中跨跨中4号截面，站桥合一结构在地震作用下，桥梁弯矩的分配模式发生相应改变。

6 结论

通过采用桥梁有限元软件Midas/Civil对站桥合一结构的动力分析以及不同工况地震波输入下的结构响应，可得出以下主要结论：

(1)站桥合一结构前五阶振动模态均为地铁车站的边跨振动，边跨振动幅度较大，中跨振动幅度较小，站桥合一结构的动力特性主要由地铁车站控制。

(2)在地铁车站影响下，钢箱梁桥基频变小，横桥向和纵桥向刚度均变小。

(3)站桥合一结构的基频小于单独钢箱梁桥的基频，而且前5阶振型中站桥合一结构的基频均小于单独钢箱梁桥的频率，说明站桥合一结构的动力特性由地铁车站控制。

(4)不同方向地震激励下，最大轴力、最大弯矩均出现在主梁跨中支座处3号截面，为桥梁抗震设计中承载力的控制截面。

(5)分析主梁控制截面的轴力时，纵向+竖向工况下的轴力最大，纵向地震波对主梁控制截面的轴力影响较大，表现为纵向地震水平力对主梁轴力的参与效应，与结构动力学理论相吻合。

(6)在纵向工况和横向工况等一维激励作用下，相对于三维激励作用，主梁跨中支座处3号截面和5号截面的负弯矩均有所增大，但增加幅度仅为5 %。

(7)最大正弯矩在中跨跨中4号截面，站桥合一结构在地震作用下，桥梁弯矩的分配模式发生相应改变。