大跨度拱桥箱梁静力三分力系数研究

郭俊峰

(中铁二十三局集团有限公司, 四川成都 610072)

目前我国公路与铁路的建设正处于高速发展期，桥梁作为连接陆路交通的重要纽带，在铁路与公路的建造中发挥着关键作用[1]。随着桥梁建造技术的不断发展以及新材料的使用，各类型桥梁的跨度不断被刷新。越来越多的大跨度桥梁被广泛地建造在山区、峡谷等复杂地形之中。现代大跨度桥梁普遍具有柔软、纤细且结构阻尼比较低的特点，因此其对风的作用变得越来越敏感。风荷载已成为大跨度桥梁建造与运营必须考虑的重要因素之一。在桥梁设计阶段，精确识别主梁截面静力三分力系数是桥梁抗风分析的基础。

桥梁抗风的主要研究手段包括风洞试验、CFD数值模拟、理论研究以及现场实测4种方法。相比于风洞试验和现场实测，CFD数值模拟具有费用低、周期短、不受试验条件限制等优点，因而被广泛应用于结构抗风分析之中。高宇琪[2]基于CFD数值模拟对东南沿海某大跨度连续梁桥箱型断面静气动力系数开展研究，识别了主梁断面的静力三分力系数，并分析了主梁截面尺寸和风攻角对静气动力系数的影响规律。吕铭泉[3]针对山区某高墩大跨度桥梁，利用CFD数值模拟对不同工况下的风场特征进行了仿真分析，研究了风攻角、主梁高度以及桥梁横坡等参数对主梁断面静力三分力系数的影响规律，同时还展示了各工况下箱梁截面周围流场的特征。樊书文[4]基于CFD数值模拟研究了风嘴角度及风嘴位置对主梁断面静力三分力系数的影响。郑史雄[5-6]等人通过风洞试验研究了斜向风作用下倒梯形桁梁桥的静气动力参数。邹明伟[7]将倒梯形桁架主梁断面简化为二维等效模型，并利用CFD数值模拟对模型进行了气动参数识别，参数结果与风洞试验吻合较好，从而验证了文中模型简化原则的合理性。

本文所研究的对象为西部峡谷地区某大跨度中承式拱桥，拱肋采用钢-混凝土结合拱方案，拱上立柱采用双柱式框架墩，主梁采用单箱三室预应力混凝土梁，其截面如图1所示。通过对比CFD数值模拟结果与风洞试验结果，验证计算模型简化的合理性及数值风洞的可靠性，从而为大跨度拱桥的设计与抗风研究提供参考。

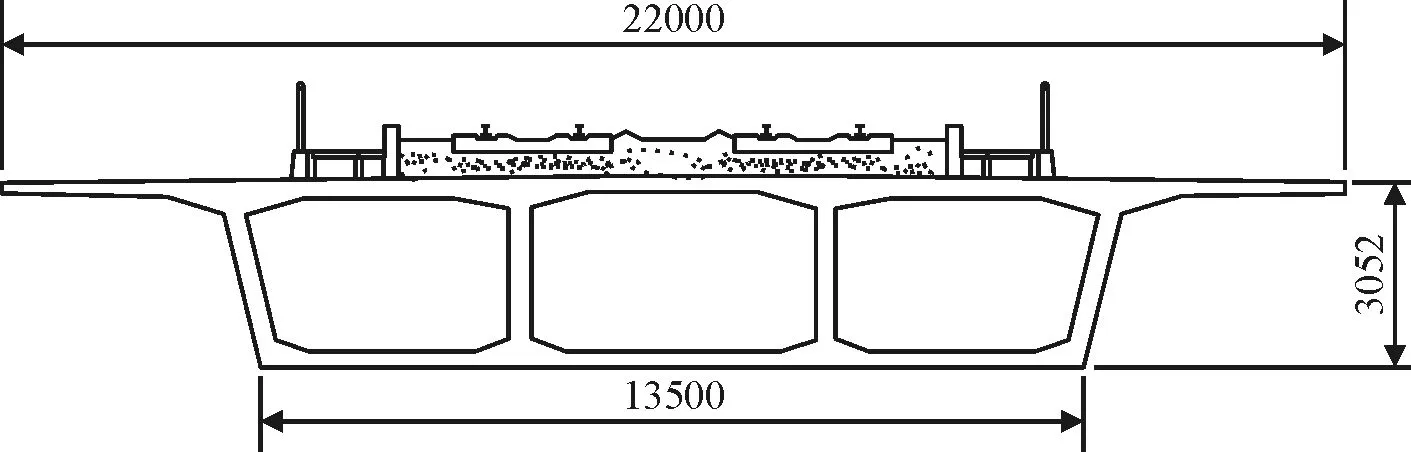
图1 主梁断面图(单位：mm)

1 CFD数值模拟

1.1 静力三分力系数

风荷载产生的本质原因是主梁气动外形改变了其周围流场分布特性[8]。在风的作用下，主梁截面会受到三个方向的静风荷载，包括阻力FH，竖向力FV以及扭矩MT。在主梁截面类似的情况下，该静风荷载与主梁截面的特征尺寸成比例。为了便于研究，引入无量纲的静力三分力系数来描述这种特征。在体轴下的静力三分力系数如式(1)所示：

(1)

式中:ρ为空气密度；D为主梁断面的高度；B为主梁断面的宽度；U为风速；CH为阻力系数；CV为升力系数；CM为升力矩系数。

1.2 计算域与网格划分

如图1所示，真实的桥梁结构十分复杂。对于现有的计算条件，要模拟各个细部结构对流场的影响很难实现，因此需要对桥梁结构进行适当的简化。本文将桥梁表面视为光滑无摩擦的壁面，同时忽略道砟板上铁轨细部结构、桥上路灯等附属结构，建立反映主要气动特性的主梁简化模型，如图2所示。

图2 简化后的主梁断面

将主梁断面如图2所示简化之后，以1∶100的几何缩尺比建立主梁模型并对数值计算域划分。合理确定数值计算域的大小和边界条件是CFD数值模拟的重要前提，同时也对计算结果的准确性有着重要影响。结合CFD计算经验与试算结果，确定如图3所示的二维计算域。

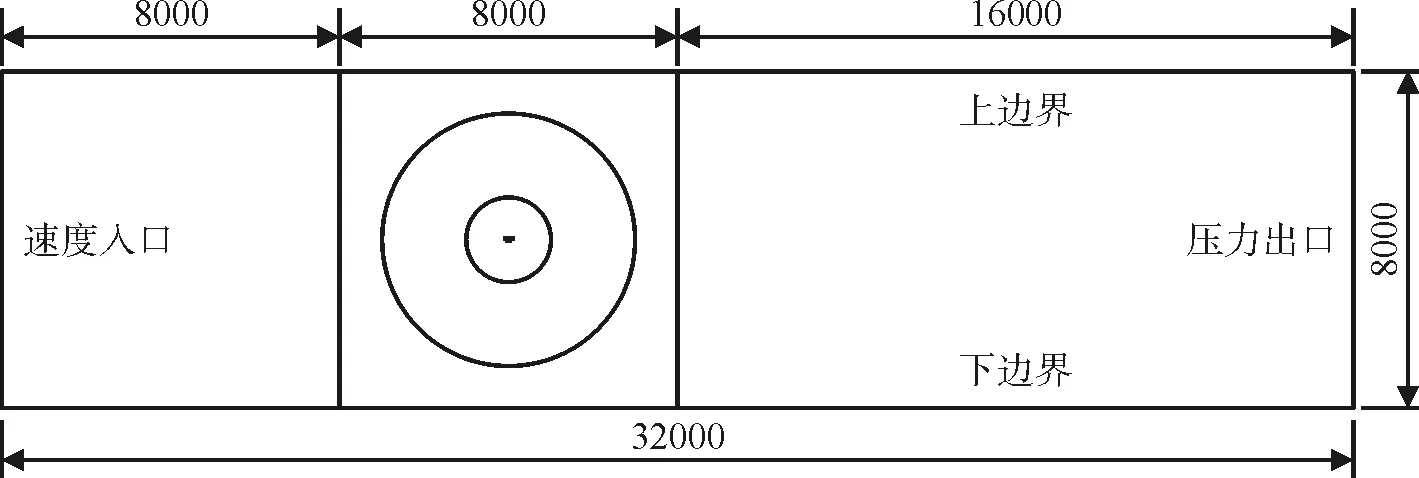
图3 流场计算域尺寸与边界条件示意(单位：mm)

计算域左侧边界为速度入口条件，右侧边界为压力出口条件，上下边界设置为对称边界条件。主梁截面设置为无滑移固定壁面边界。结构中心距入口边界为12 m，距出口边界为20 m，距上、下边界均为4 m。

在距结构最近的圆形区域采用非结构化网格，其余区域采用结构化网格，结构表面网格尺寸为1 mm，相邻网格之间的膨胀率为1.05，主梁断面附近的网格划分见图4。

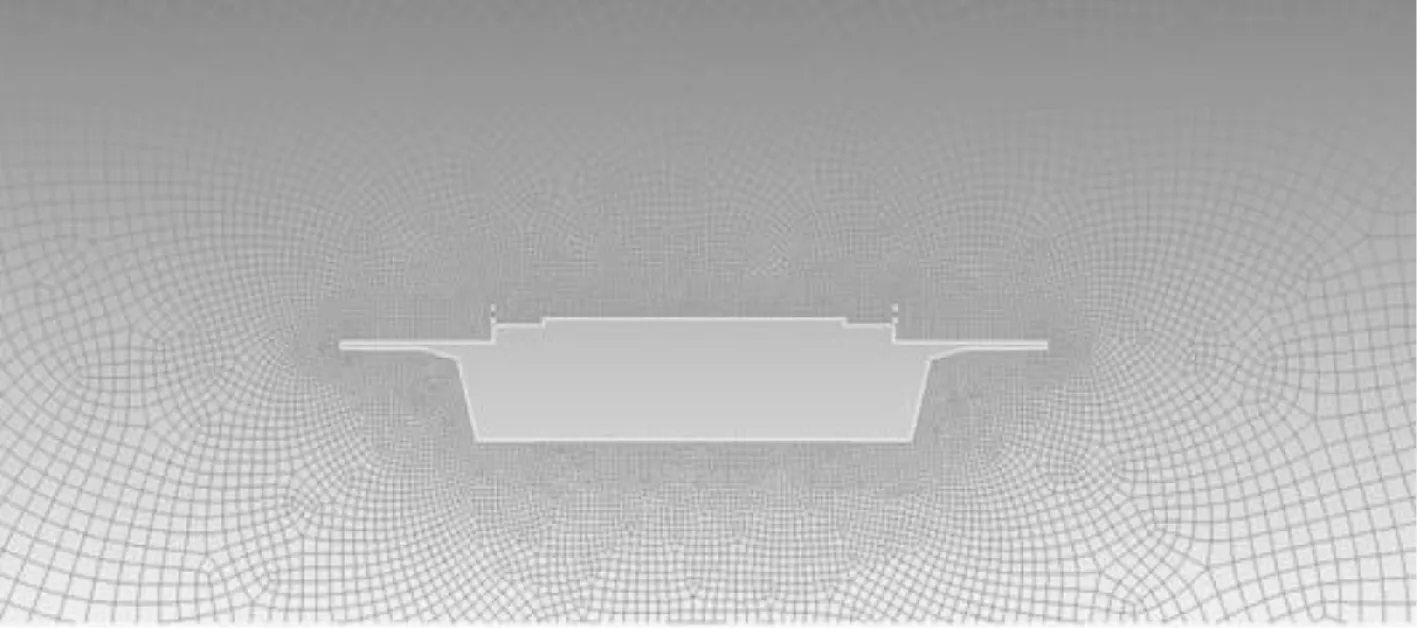
图4 主梁断面周边网格划分

1.3 静力三分力系数的识别

结合工程需要，选取风攻角a的变化范围为-5 °、-3 °、0 °、+3 °、+5 °。将5种不同风攻角工况下的流场进行划分，并在有限元分析软件的Fluent模块中进行计算。计算参数设置如下，来流速度U=20 m/s，采用SSTk-ω湍流模型，湍流强度0.5 %，湍流粘度比取2。

待计算完成后，提取各工况下主梁断面的阻力，升力与升力矩。将各参数代入公式(1)即可得到主梁断面在体轴系下的静力三分力系数(风轴系下的三分力系数可通过坐标转换得到)，如图5所示。

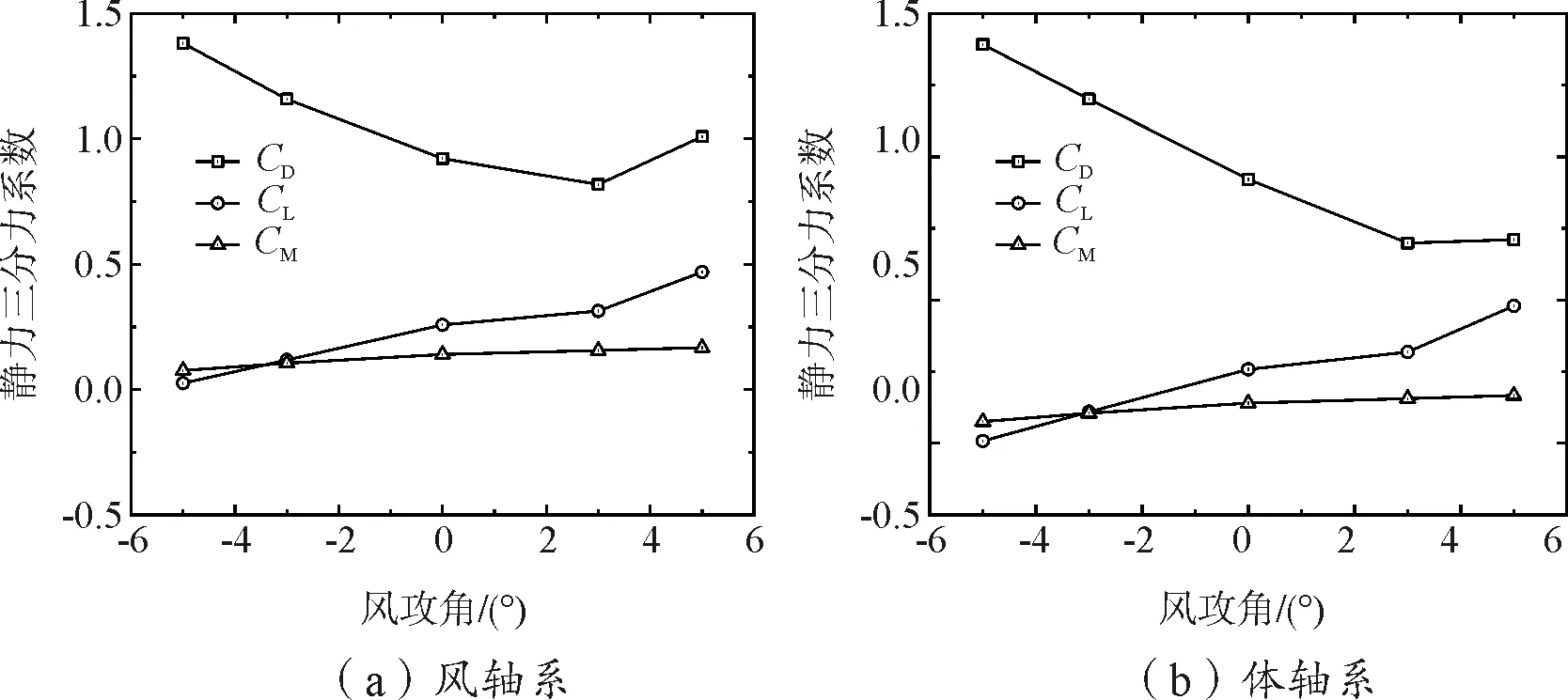
图5 主梁断面静力三分力系数

2 风洞试验

为了验证本文所采用计算模型简化的合理性以及CFD数值模拟的精确性，特地设置一组节段模型风洞试验，并将试验值与CFD计算值对比。风洞试验截面尺寸为2.0 m(高)×2.4 m(宽)的矩形，考虑到风洞尺寸，主梁节段实际尺寸以及试验要求等因素，该主梁节段模型根据实桥尺寸采用1∶40的几何缩尺比制作。主梁模型高为76.3 mm、宽为550 mm、对应的主梁实际尺寸高为3.05 m，宽为22 m。悬挂于风洞中的模型见图6。通过数据采集和分析系统可测出主梁在静风作用下的阻力、升力和升力矩，进而可得主梁的静力三分力系数。将试验结果与CFD计算值进行比较(这里仅比较风轴系下的静力三分力系数，体轴系同理)，如表1所示。

图6 主梁风洞试验模型

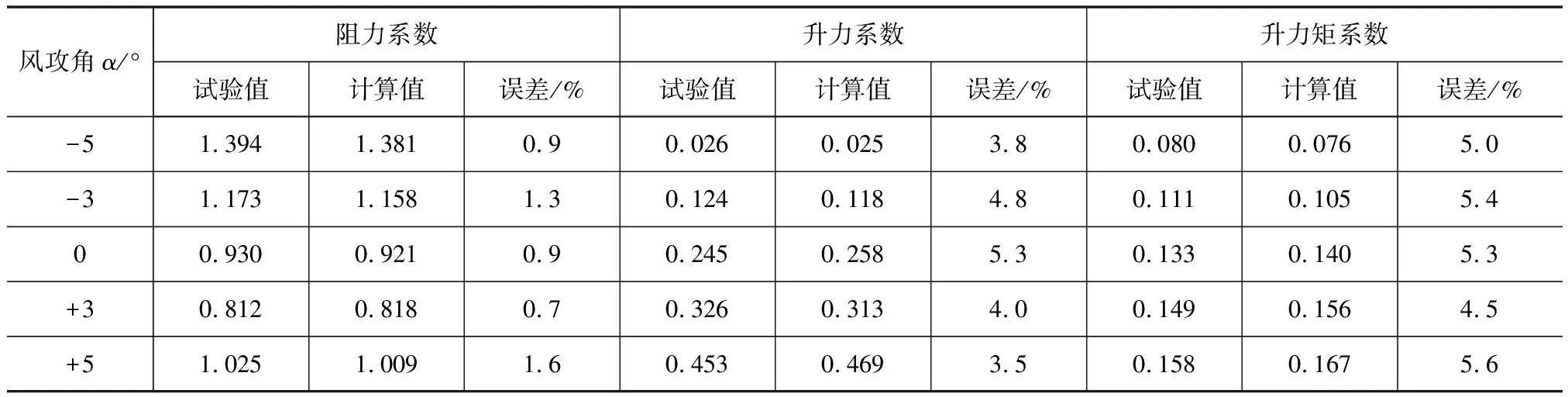
表1 主梁静力三分力系数的CFD计算值与试验值对比

从表1可以看出，基于CFD数值模拟的结果与风洞试验结果吻合较好，阻力系数误差最大值为1.6 %，对应的风攻角为+5 °；升力系数误差最大值为5.3 %，对应的风攻角为0 °；升力矩系数误差最大值为5.6 %，对应的风攻角为+5 °，均满足工程精度需求。对于同一风攻角来说，阻力系数CFD数值 模拟的精度最好，升力系数CFD数值模拟的精度次之，升力矩系数CFD数值模拟的精度较低。

3 结束语

本文分别采用CFD数值模拟与风洞试验的方法分析了西部峡谷地区某大跨度中承式拱桥的静力三分力系数，并对比分析了两种方法的计算结果，可得如下结论：

(1)文中所述的二维简化计算模型是合理的，基于CFD数值模拟的计算结果与风洞试验结果吻合良好，满足工程精度要求，可为桥梁设计及抗风性能分析提供参考。

(2)对于同一风攻角来说，阻力系数的CFD数值模拟精度最好，升力系数的CFD数值模拟精度次之，升力矩系数的CFD数值模拟精度较低。