含DG配电网故障定位的免疫二进制萤火虫算法
2021-06-04周年荣李英娜
杨 莉 周年荣 李 川 李英娜 杨 鑫
(1.云南电网有限责任公司电力科学研究院;2.昆明理工大学信息工程与自动化学院)
随着电网的不断发展升级,已有许多分布式电源(Distributed Generation,DG)并入电网。从电网面向用户供电可靠性角度考虑,在电网发生故障后,准确且快速实现故障区段的确定与故障排除是非常有必要的[1]。目前已被广泛使用的定位算法主 要包括矩 阵 算法[2,3]和 人工 智 能 算法[4]两大类。矩阵算法具有原理简单和运行速度快的优势,但其计算准确性很大程度上依赖馈线终端单元反馈数据的真实性,当数据失真时,这类算法就容易造成错判与漏判。而基于人工智能算法的配电网故障定位方法实现相对复杂,但具有较高的容错定位能力。
文献[4]中的改进配电网故障定位数学模型,借鉴广义分级思想将配电网划分为不同优先级区域,提升了故障定位的效率,但研究局限于环网开环运行的配电网;文献[5]所提的配电网故障定位的二进制粒子群(BPSO)算法表现出良好的容错性,但未考虑DG对故障区段定位的影响;文献[6,7]均改进了二进制粒子群算法,能够提高定位收敛速度,但这些改进也在一定程度上加大了算法的实现难度,且文献仅针对单电源配电网故障定位。此外,蝙蝠算法[8]、仿电磁学算法[9]及蚁群算法[10]等其他人工智能算法 也是经常被使用的算法。但这些方法在解决大规模优化问题时需要大量的初始种群数据,且易陷入局部最优。在文献[11]中,研究了一种适用于配电网故障区段的免疫二进制萤火虫算法(IBFA),仿真试验表明算法具有较好的容错性与收敛速度。
DG的接入导致配电网中故障电流的流向由原先单电源配电网中的单向流动变为双向流动,故障电流的分布情况发生了改变[12]。此外,在具有多处DG的配电网中,故障电流流经的线路区段数量有所增加,这些变化给配电网故障区段造成了一定的影响[13]。DG的并入导致针对单电源配电网故障区段定位的方法不再适用。笔者在文献[11]的基础上继续展开研究,将IBFA应用到含DG配电网故障区段定位中。仿真试验结果表明,算法在收敛性与容错性上都比二进制粒子群算法有更好的表现。
1 基于IBFA的含DG配电网故障区段定位原理及其算法
1.1 故障区段定位原理
与不含DG配电网一样,含DG配电网线路区段运行状态仍分为0和1两种情况,0表示该区段正常运行,1表示该区段出现短路故障。当网络内某线路区段出现短路故障时,馈线终端装置(FTU)会把检测到的故障电流越限信息上传至控制中心。为了提升算法的收敛速度,将记忆池与免疫算法的思想添加入萤火虫算法中,形成免疫二进制萤火虫算法,通过记忆池的动态更新保存当前迭代最优结果,借鉴免疫算法基因座的思想计算种群内个体的相似度,迭代过程中以一定的概率剔除相似度低的边缘个体。在IBFA中,每个萤火虫个体的位置都是一组解,每次迭代时需计算种群中每一组解的评价函数值,然后将评价函数值转换为萤火虫的发光强度,光强越大表示该萤火虫对应的解越接近最优解,即真实的线路区段运行状态。萤火虫个体会搜寻周围靠近自己且比自身更亮的个体,然后朝着目标个体移动,最终实现整体收敛的效果。迭代寻优完成时,IBFA的最优解即对应待求解配电网中各线路区段的实际运行状态。从数学模型上看,含DG配电网故障区段定位问题本质上是一个具有0-1离散约束条件的最优化问题,可以通过笔者所提的IBFA进行优化求解,准确、快速地定位出故障区段。
1.2 开关函数
含DG配电网中的故障电流流向与仅有单供电电源的配电网有很大不同,更加复杂。因此,对含DG配电网所需构建的开关函数与不含DG配电网的存在明显差异。
通过详细分析含DG配电网的结构特点,笔者以整个结构中某一开关节点j作为分段点,将整个配电网结构划分为上半区和下半区两部分。规定含有主供电电源的部分为j的上半区部分,其余部分为j的下半区部分。同时规定网络中故障电流流向的正方向为整个系统主电源指向用户的方向。安装在开关节点j处的FTU若检测到故障越限电流,需与规定的正方向对比,若方向一致则向控制中心上报故障信息1,若方向相反则上报故障信息-1,未检测到则上报0。
现以图1含2处DG的简化配电网模型为例,其中S为配电网主电源;1~6为配电网中的6个开关节点;L1~L6为配电网中的6个线路区段;K1、K2分别为决定DG1、DG2是否并入配电网的开关。若线路区段L3发生短路故障,则各FTU(1~6)上报的故障信息序列为[1,1,1,-1,-1,-1]。上述规定的优势在于,只需确定一次正方向,便可实现含DG配电网的多重故障区段定位[14]。

图1 含2处DG的简化配电网模型
笔者采用的开关函数为:
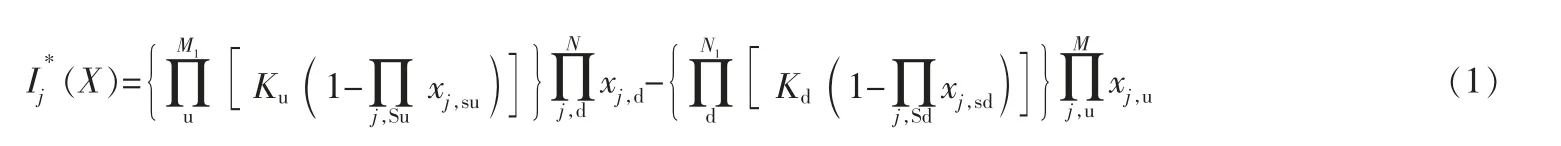
其中,符号Π表示逻辑“或”运算;u和d分别表示节点j的上半区和下半区部分;Ku、Kd分别表示j的上半区和下半区中电源是否并入配电网的开关系数,当有电源并入时取1,否则取0,其中主供电电源系数保持为1;M1、N1分别表示节点j上半区和下半区所包含电源的数量;xj,su、xj,sd分别表示节点j到上半区、下半区电源所经过线路区段的运行状态值;xj,u、xj,d则 分别表示节点j上半区、下半区所有线路区段的运行状态值;M、N分别表示节点j上半区和下半区线路区段总数。
1.3 评价函数
参考文献[15],笔者采用的评价函数为:


1.4 算法运行流程
算法运行流程如图2所示。
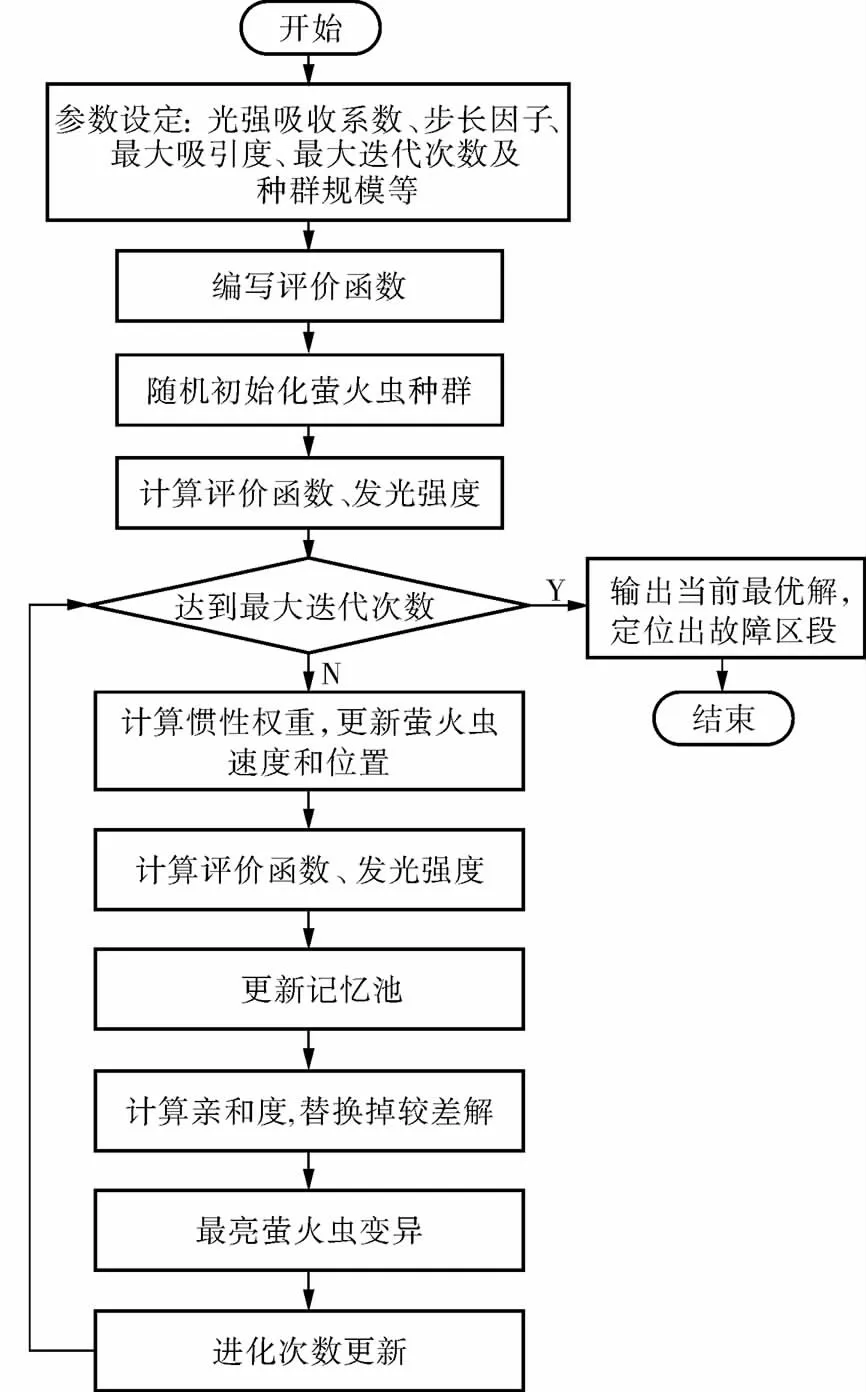
图2 算法运行流程
2 实例分析
笔者采用如图3所示的含3处DG的配电网模型进行仿真试验。图3中S为系统主电源;K1、K2和K3分别为决定DG1、DG2和DG3是否并入配电网的开关;1~30为配电网中的30个开关节点;L1~L30为配电网中的30个线路区段。仿真试验时设置L1~L30中不同线路区段故障,来模拟配电网中发生的单点与多点故障,运行笔者所提的IBFA进行故障区段定位试验,同时运行BPSO算法进行对比,验证笔者所提算法在含DG配电网定位中的可行性与快速收敛性。在故障区段定位开始之前对算法程序进行相应初始化,两种算法均设定最大迭代次数T=100,其中IBFA的种群规模设定为M1=50、光强吸收系数设定为γ=0.2、步长因子设定为α=0.1、最大吸引度设定为β0=1.0;BPSO算法的种群规模设定为M2=100、学习因子c1=c2=1.494。
2.1 单点故障
当配电线路发生单点故障,且DG位置不同,DG并入配电网的数量不同,FTU上报的故障信息存在不同程度的畸变时,故障区段仿真定位结果见表1,该试验结果为多次仿真定位结果。从表1可以看出当发生单点故障时,在不同位置、不同数量的DG并入且FTU上报信息存在不同位数畸变的情况下,笔者所提IBFA均能准确定位出故障线路区段。
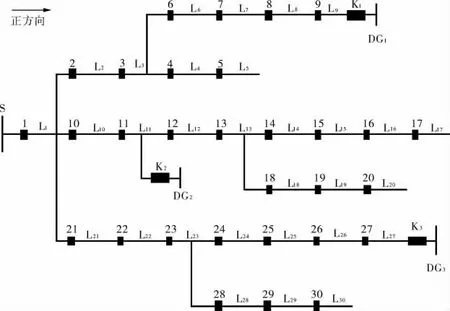
图3 含3处DG的配电网模型

表1 单点故障仿真定位结果
图4为配电网线路区段L8故障、DG全部并入且23开关节点处发生信息畸变时,两种算法定位结果收敛对比结果,该结果为一次试验的结果对比。IBFA与BPSO均准确定位出故障区段,但IBFA仅需迭代计算40次即可定位出故障区段,而BPSO算法则需迭代计算74次,说明IBFA具有更快的收敛速度。
2.2 多点故障
设置与单点故障相同的故障条件,仿真定位多点故障,定位结果见表2,该试验结果为多次仿真定位结果。从表2可以看出当发生多点故障时,在不同位置、不同数量的DG并入且FTU上报信息存在不同位数畸变的情况下,笔者所提IBFA均能准确定位出故障线路区段。

图4 单点故障有1位信息畸变时两种算法的对比

表2 多点故障仿真定位结果

(续表2)
图5为配电网线路区段L3、L14发生故障,DG全部并入且21开关节点处发生信息畸变时,两种算法定位结果收敛对比结果,该结果为一次试验的结果对比。IBFA算法迭代计算23次就已经定位出故障区段,而BPSO算法则迭代计算100次仍未能定位出故障区段。

图5 多点故障有1位信息畸变时两种算法的对比
2.3 故障定位性能对比
现以出现“未成熟收敛”现象次数作为衡量指标,评价在配电网故障区段定位时IBFA与BPSO算法的性能。利用两种算法分别对预设的同一位置单点故障进行定位试验,两种算法各自连续运行50次,然后预设多点故障,试验方法与单点故障时相同,IBFA与BPSO算法出现“未成熟收敛”次数统计结果见表3。

表3 两种算法出现“未成熟收敛”现象的次数
由表3的统计结果可以看出,在使用BPSO算法定位含DG配电网的故障区段位置时,会出现“未成熟收敛”现象,且出现次数会随故障点数量的增加而增加;而使用笔者所提IBFA时,则没有出现该现象。
以单点故障(L8)连续50次试验为例,IBFA最少只需迭代21次,最多需迭代49次,平均为30.4次;而BPSO最少需要迭代23次,且出现了表3中的2次“未成熟收敛”现象,去除2次“未成熟收敛”,平均需要迭代53.2次。多点故障与单点故障类似,IBFA的收敛速度快,更容易得出全局最优解,避免不必要的冗余迭代。
3 结束语
笔者使用IBFA完成含DG配电网故障区段的定位。采用记忆池与免疫算法结合增强算法的寻优能力,并将该算法应用于包含DG的配电网故障区段定位中。在拥有30个节点、3处DG的配电网模型中进行仿真试验,假设线路发生单点与多点故障,在信息完整与发生信息畸变情况下采用IBFA进行故障定位。试验结果表明:存在不同数量、位置的分布式电源并入电网,且存在不同位数信息畸变的情况下,笔者所提IBFA仍能准确定位出含DG复杂配电网的故障区段,体现出较强的容错性。与BPSO算法相比,IBFA在运行时间和查找全局最优解问题上具有更好的表现。
