冲击载荷下螺栓预紧力对应力波影响分析

杨璞，谢若泽，陈刚，陈成军

（1.中国工程物理研究院总体工程研究所，四川 绵阳 621900；2.工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621900）

武器在转移、输运及装卸等情况下，可能面临意外碰撞等异常环境[1]。异常事故产生的冲击载荷可能导致武器各部组件经历冲击高应力、塑性大变形破坏以及诱使炸药构件点火。因此为了合理评估异常冲击环境下武器的安全性，需充分认识冲击载荷作用下应力波在武器连接结构中的传播规律。螺栓连接是武器结构中常见的连接方式，采用螺栓连接时，一般都会施加预紧力[2]。使螺栓连接在承受工作载荷之前，提前受到力的作用，这个预加作用力称为预紧力[3]。螺栓预紧力可增强连接的紧密性和刚性[4]。当结构受到冲击载荷时，螺栓会受到较大的拉应力，该状态下，螺栓预紧力可能会对结构应力波传递产生一定的影响。在实际工程分析中，常忽略螺栓预紧力，甚至将螺栓连接简化为固定连接的节点，这与实际情况有较大出入。

另一方面，针对螺栓预紧力的研究多为静力载荷下的响应分析[5-8]，冲击载荷下的响应分析较少，且未见预紧力对应力波传递影响规律的研究。史冬岩等人[9]分析了冲击载荷下螺栓预紧力大小对螺栓强度的影响。Karpanan Nakalswamy等人[10]研究了冲击载荷下预紧力对结构模态的影响，另外他们还对比了不同预紧力加载方式的计算精度[11]。目前，关于冲击载荷下螺栓预紧力对应力波传递的影响分析相对匮乏。

基于此，文中针对拉伸冲击载荷作用下螺栓预紧力对螺栓连接的影响规律进行数值模拟，对螺栓弹性变形、塑性变形和冲击破坏3种情形进行数值模拟，对比分析了螺栓没有预紧力及不同预紧力下螺栓和连接结构的响应特性。最后以霍普金森拉伸实验为基础，验证了数值模拟预紧力加载的正确性。

1 连接结构有限元模型

1.1 结构尺寸

螺栓连接结构由截锥和圆筒组成，截锥和圆筒由法兰面上的4颗螺栓连接，右端撞击杆撞击输入杆使左端结构承受拉伸载荷，螺栓受拉。模型结构如图1所示，各部分尺寸见表1。

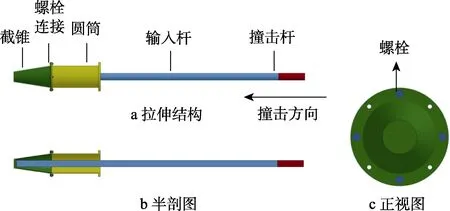
图1 连接结构受拉伸载荷Fig.1 Connection structure subjected to tensile impact load: a)tensile structure; b) half section; c) front view

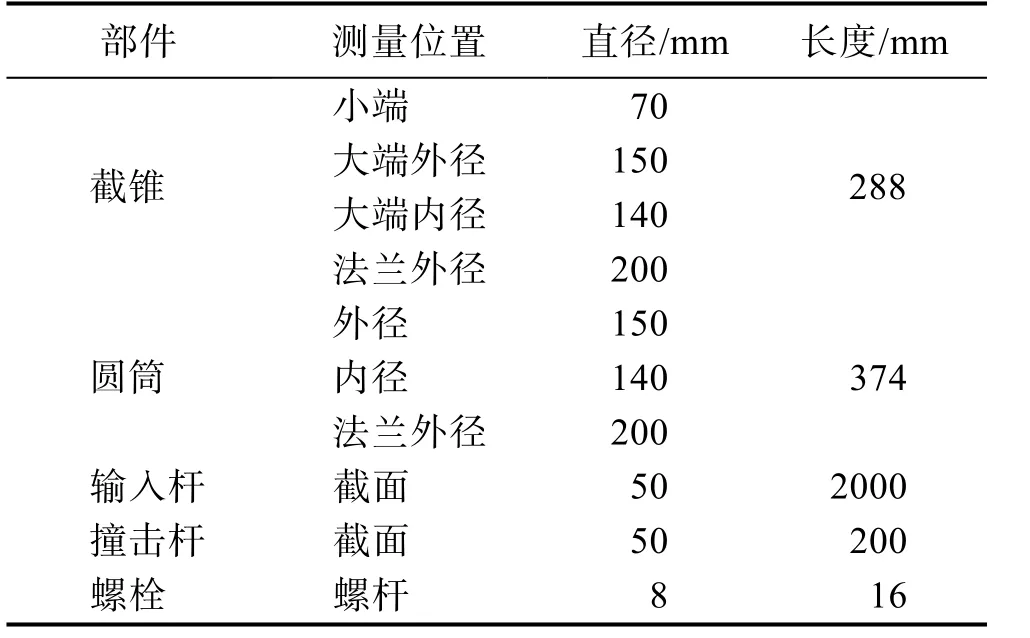
表1 连接结构尺寸Tab.1 Size of Connection structure

1.2 材料参数

连接结构的截锥、圆筒及螺栓材料采用弹塑性模型，杆件材料采用弹性模型，具体参数见表2。使螺栓产生塑性变形及断裂时所用输入杆和撞击杆为钢材。考虑到螺栓产生弹性变形时所需的冲击力极小，故使螺栓产生弹性变形时所用输入杆和撞击杆均为铝材。

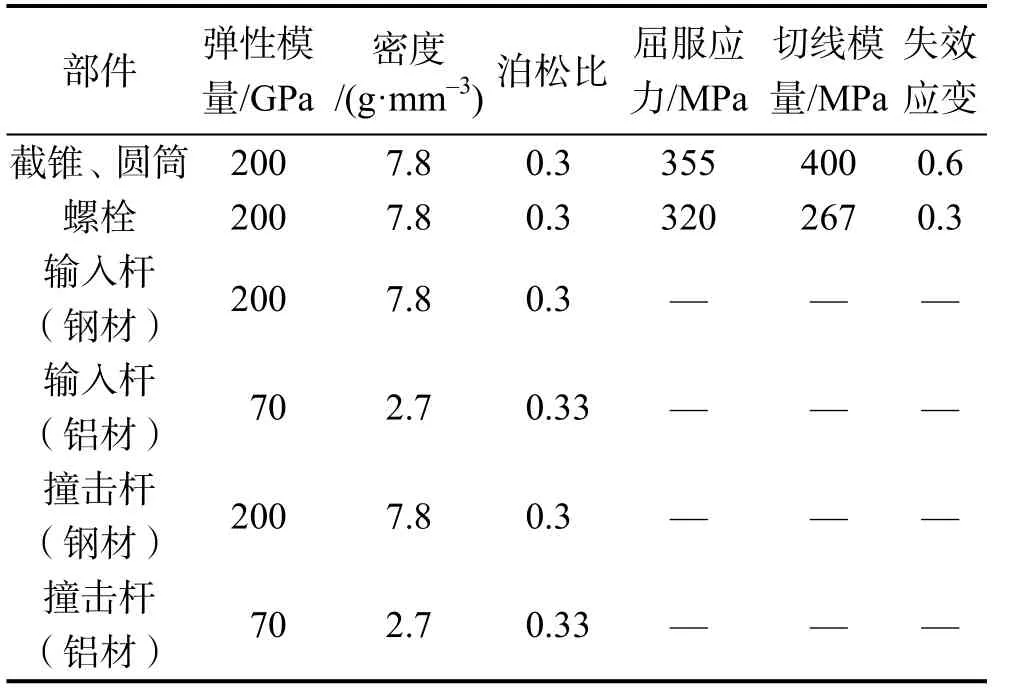
表2 连接结构、输入杆及撞击杆材料参数Tab.2 Material parameter of connection structure、incident bar and striker bar

2 预紧力模拟方法及入射波幅值选取

2.1 预紧力加载方式

数值模拟中可采取多种方法对螺栓施加预紧力，如初应力单元法、初始渗透法、降温等效法等[12]。文中采用降温等效法，即先使螺栓轴向与法兰面过盈配合，其后对螺栓升温，使其轴向长度膨胀至大于法兰厚度，再对螺栓温降。由于螺栓的收缩受到紧固件的限制，使得螺杆受拉，被紧固件受压，通过这样的原理就能通过降低温度来等效施加螺栓预紧力[6]。经典的设计惯例是螺栓的预紧力一般可达螺栓屈服强度的50%～70%[13-14]。以此为基准设计了3组预紧力，各预紧力及螺栓过盈量见表3。

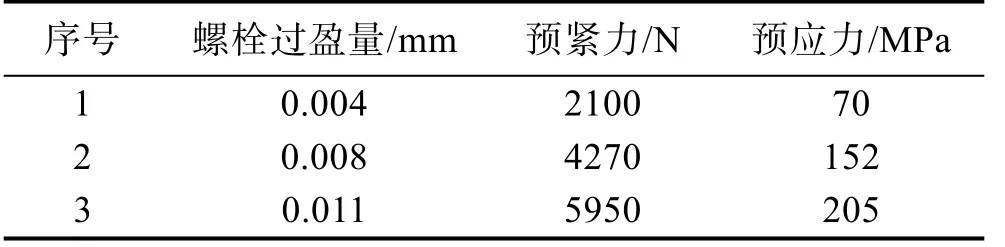
表3 螺栓预紧力加载情况Tab.3 Magnitude of different pre-loads

2.2 入射波幅值

霍普金森杆撞击产生的入射波幅值公式为[15]：

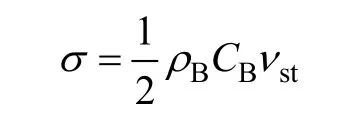
式中：ρB为杆材料的密度；CB为弹性杆中的波速；vst为撞击速度。

为确定不同状态下所需入射波幅值，首先对不同撞击速度下螺栓的响应进行初步分析，得到螺栓弹性变形、塑性变形及断裂时对应的速度范围：铝杆撞击速度vst≤2 m/s时，螺栓弹性变形；钢杆撞击速度为2～43 m/s时，螺栓塑性变形；钢杆撞击速度vst≥43 m/s时，螺栓断裂。最终选取撞击速度2、20、50 m/s分别模拟螺栓弹性变形、塑性变形和冲击破坏3种情形。此时3种撞击速度下的入射波幅值分别为13.5、390、975 MPa。

3 计算结果分析

3.1 截锥圆筒上测点应变分析

为分析应力波在结构中的传递规律，在截锥及圆筒上沿母线方向布置测量点，记录轴向应变。各测点分别位于截锥壳外侧面沿母线方向锥头、中部和锥底位置，圆筒部件外侧面中部，各测点分布如图2所示。其中测点1、2、3、4、5、6与截锥部件小端面的距离分别为20、100、185、268、380、567 mm。

图2 连接结构上应变测点分布Fig.2 Position of measuring points on connection structrue

3.1.1 入射波幅值975 MPa

入射波幅值为975 MPa时，螺栓最终被拉断。测点1在输入杆的撞击下发生塑性变形，其他测点未产生塑性变形。

无预紧力及不同预紧力下各测点的轴向应变对比如图3所示。图3a—d反映出无预紧力和有预紧力的测点应变曲线基本重合，其对应的测点1—4均在截锥上，应变受入射波和反射波的叠加作用。由于螺栓只对反射波产生影响，所以可见螺栓有无预紧力对反射波影响不大。图3e、f反映出有无预紧力测点的应变曲线峰值存在一定差异，其对应的测点5、6在圆筒上，其应变反映了透射波作用。可见螺栓有无预紧力对透射波有一定的影响。

3.1.2 入射波幅值390 MPa

图3 入射波幅值为975 MPa时各测点轴向应变对比Fig.3 Axial strain comparison of measuring points when the incident wave amplitude is 975 MPa: a) measuring point 1; b) measuring point 2; c) measuring point 3; d) measuring point 4; e) measuring point 5; f) measuring point 6

入射波幅值为390 MPa时，螺栓最终产生塑性变形。和入射波幅值975 MPa时一样，截锥上测点1发生塑性变形，其他各测点均未产生塑性变形。在撞击过程中，截锥和圆筒法兰界面先分离，直至螺栓产生最大塑性变形时，两法兰界面不再受螺栓接触力，其后两法兰界面又将重新接触，如图4所示。截锥与圆筒法兰间隙的变化历程如图5所示，其反映出两界面再次接触的时刻约为t=1.8 ms。

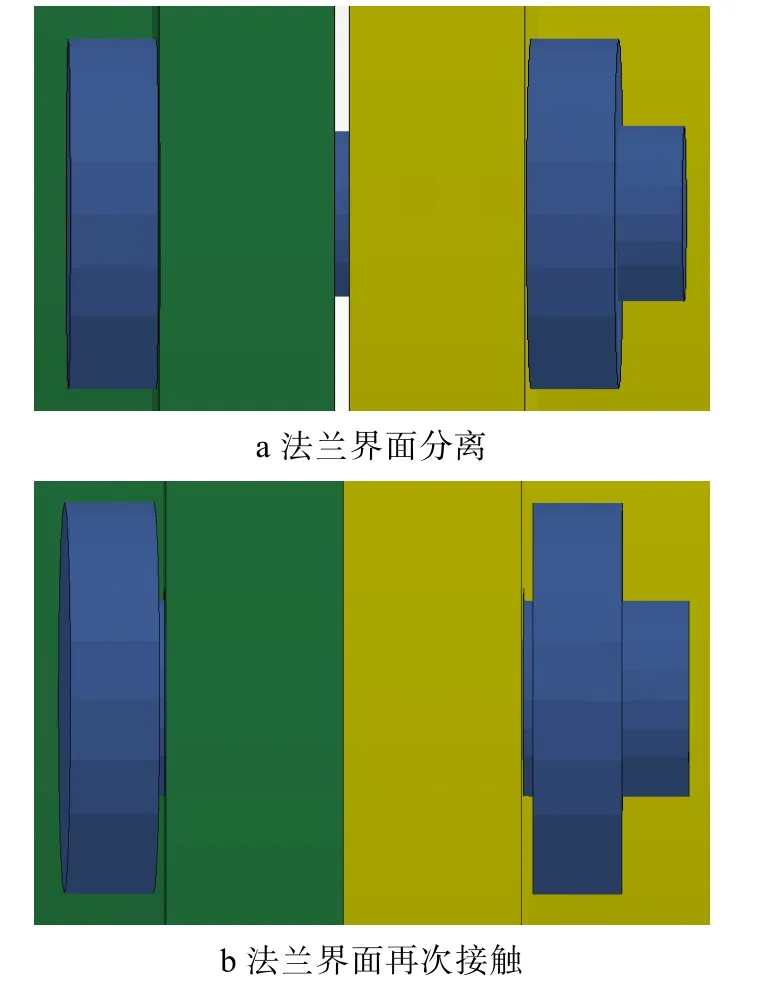
图4 入射波幅值为390 MPa时撞击过程中连接界面运动示意Fig.4 Indication of connection interface motion when the incident wave amplitude is 390 MPa: a) flange interface separation; b) flange interface contacts again

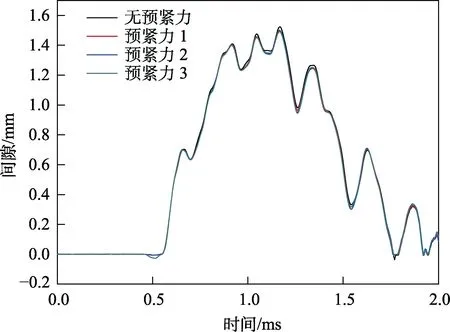
图5 入射波幅值为390 MPa时撞击过程中截锥与圆筒界面间隙变化历程Fig.5 Time history of distance variation between truncated cone and cylinder when the incident wave amplitude is 390 MPa

入射波幅值为390 MPa时，无预紧力及不同预紧力下各测点轴向应变对比如图6所示。由图6a—d可以看出，测点应变曲线在t=1.8 ms前基本重合；t=1.8 ms后，两曲线出现轻微差异，即两法兰再次接触对测点应变有影响，但影响很小。同样因为测点1—4均在截锥上，所以螺栓预紧力对反射波影响不大。图6e、f反映出测点应变曲线在t=1.8 ms前存在一定差异，t=1.8 ms后差异增大。同样对应的测点5、6在圆筒上，其应变受透射波作用，再次证明螺栓有无预紧力对透射波有一定的影响。

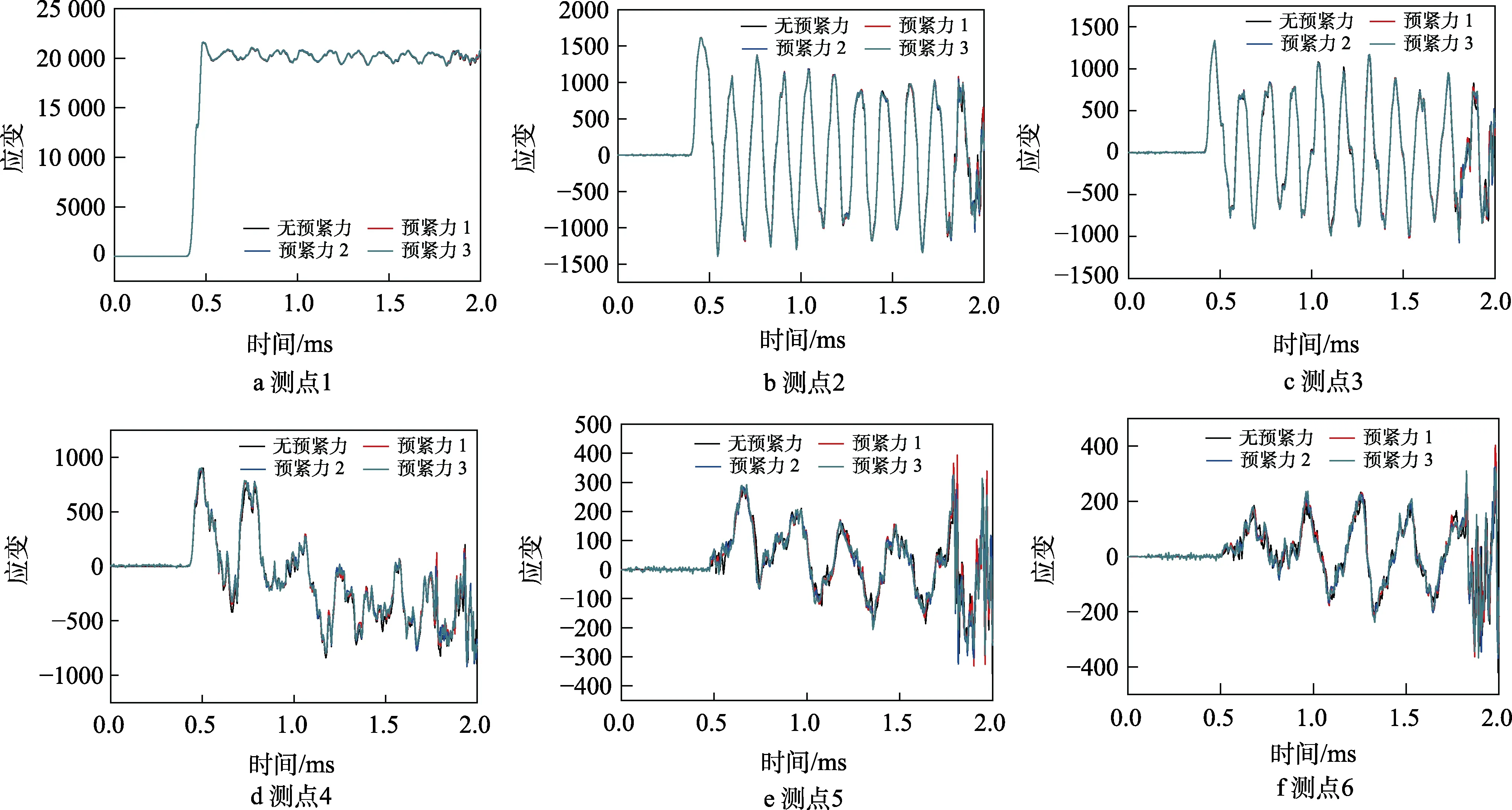
图6 入射波幅值为390 MPa时各测点轴向应变对比Fig.6 Axial strain comparison of measuring points when the incident wave amplitude is 390 MPa: a) measuring point 1; b) measuring point 2; c) measuring point 3; d) measuring point 4; e) measuring point 5; f) measuring point 6

3.1.3 入射波幅值13.5 MPa

入射波幅值为13.5 MPa时，螺栓最终产生弹性变形，截锥圆筒上各测点均未产生塑性变形。截锥与圆筒法兰间隙的变化历程如图7所示。由图7可见，在撞击过程中，截锥和圆筒法兰界面先分离、后接触。因为螺栓预紧力限制了两法兰分开的距离，所以预紧力越大，界面越先接触，截锥和圆筒再次接触时刻分别为0.76、0.80、0.83、0.94 ms。

无预紧力及不同预紧力下，各测点的轴向应变如图8所示。图8a—c反映出测点1—3的应变曲线在t=0.76 ms前基本重合，t=0.76 ms后，两曲线出现差异，即两法兰再次接触的时刻不同造成了应变曲线的差异。有别于前文螺栓最终断裂和产生塑性变形2种状态，螺栓只产生弹性变形时，预紧力全程作用在截锥和圆筒上，预紧力通过影响截锥和圆筒的运动进而影响反射波传播历程。从图8d可以看出，从撞击杆撞击结构时刻开始，无预紧力及不同预紧力下，测点4的应变曲线就产生差异。这是因为测点4离预紧力区域近，且2 m/s撞击时产生的应变较小，相对于撞击产生的变形，预紧力在该处造成的应变不可忽略，因此测点4应变曲线从一开始就表现出差异。图8e、f反映出测点应变曲线峰值存在一定差异，同样是因为预紧力影响了截锥和圆筒的运动，进而影响了透射波的传播历程。

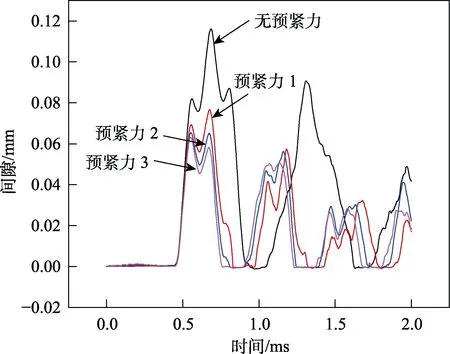
图7 入射波幅值13.5 MPa时撞击过程中截锥与圆筒界面间隙变化历程Fig.7 Time history of distance variation between truncated cone and cylinder when the incident wave amplitude is 13.5 MPa

图8 入射波幅值13.5 MPa撞击时不同预紧力下各测点轴向应变对比Fig.8 Axial strain comparison of measuring points when the incident wave amplitude is 13.5 MPa: a) measuring point 1; b)measuring point 2; c) measuring point 3; d) measuring point 4; e) measuring point 5; f) measuring point 6

3.2 螺栓响应分析

3.2.1 螺栓应力

螺栓应力随时间的变化曲线如图9所示。对各幅值的入射波，t=0.46 ms时刻，截锥上的应力波传至螺栓，在这之前螺栓应力维持在初始预应力水平。

入射波幅值为975 MPa时，t在0.46～0.80 ms为螺栓拉伸至断裂阶段。该阶段各曲线重合，但考虑到其初始应力不同，对应的应力增大幅值也不同，即预应力越大，拉断所需的应力越小。这是因为预紧力越大，应力值越靠近拉伸强度极限。螺栓在t=0.80 ms时刻断裂，其后应力曲线出现震荡，且不再重合。

图9 3种入射波幅值时不同预紧力下的螺栓应力对比Fig.9 Bolt stress comparison between multiple pre-loads when the incident wave amplitude is 975, 390, 13.5 MPa

入射波幅值为390 MPa时，t在0.46～0.86 ms为螺栓拉伸至最大塑性应变阶段。该阶段各曲线重合，是因为预紧力越大，预应力值越靠近屈服强度，螺栓达到最大塑性变形所需的拉伸应力越小。螺栓在t=0.86 ms时刻产生最大塑性变形，其后螺栓与截锥圆筒的法兰面分离，作自由运动，应力曲线出现震荡，且不再重合。

入射波幅值为13.5 MPa时，螺栓处于弹性变形，应力幅值先上升至屈服应力，然后降至各自的初始应力水平。应力曲线同样遵循预应力越大，拉伸时产生的应力越小的规律。

3.2.2 螺栓变形

各撞击速度与预紧力下螺栓的最大变形量见表4。入射波幅值为975 MPa时，螺栓断裂，无最大变形量；入射波幅值为390 MPa时，螺栓产生塑性变形，用最大等效塑性变形量表征；入射波幅值为13.5 MPa时，螺栓产生弹性变形，用最大等效应变表征。由表4可以看出，入射波幅值为390 MPa时，螺栓预紧力对螺栓最终塑性变形影响不大；入射波幅值为13.5 MPa时，螺栓预紧力越高，其变形越大，这是因为该速度下螺栓因撞击产生的变形与预紧力产生的变形同量级，螺栓变形受预紧力变形影响较大。

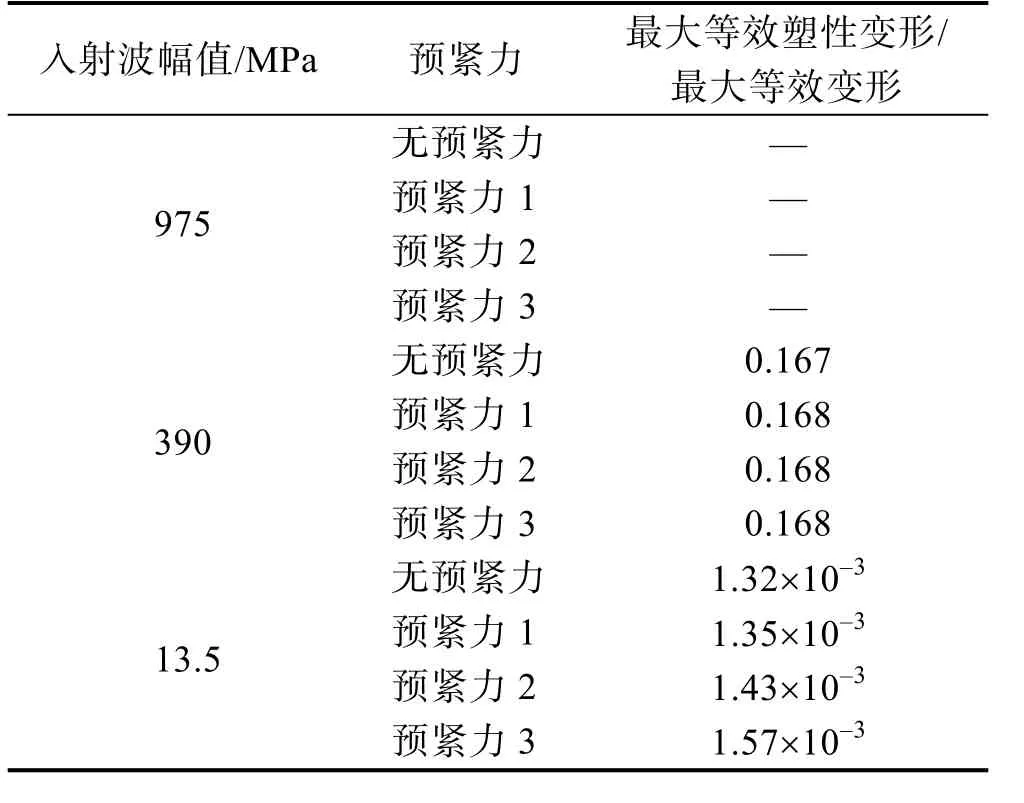
表4 3种入射波幅值时不同预紧力下螺栓最大变形对比Tab.4 Maximum strain comparison of bolt between multiple pre-loads when the incident wave amplitude is 975/390/13.5MPa

3.2.3 最低撞击速度

因螺栓断裂时无法用塑性变形量来分析其响应，故以螺栓刚好断裂时所需撞击速度来表征其响应。螺栓被拉断所需的最小撞击速度见表5。由表5可见，无预紧力及不同预紧力下，拉断螺栓所需的最小撞击速度接近，速度差最大仅为0.47%，故预紧力对螺栓断裂影响较小。

表5 不同预紧力下螺栓断裂所需最小撞击速度Tab.5 Minimum launching velocity needed to achieve bolt failure when different pre-loads are applied

4 实验结果

为验证数值模拟中螺栓预紧力加载方式的合理性，将相同工况下数值模拟与霍普金森撞击实验的测点应变曲线进行对比。对比工况：撞击杆长度为200 mm，撞击速度为9.63 m/s，撞击杆和输入杆均采用钢，预紧力为6000 N。实验中测点位置如图10所示，测点1、2、3、4、5、6、7与截锥部件小端面的距离分别为20、100、180、260、356、471、586 mm。数值模拟中在相同测点位置提取轴向应变数据。

图10 连接结构霍普金森撞击实验装置Fig.10 Connection structure subjected to SHPB experiment

各测点实验和数值模拟轴向应变对比结果如图11所示。各测点第一个波峰的波宽及波峰对比见表6。结果表明，除测点1、4数值模拟与实验结果差距较大外，其他点第一个波峰数值模拟与实验结果基本一致。测点1和测点4位置接近截锥的两端受干扰较大，故数值模拟与实验结果差距较大。其他5个测点数值模拟和实验结果第一个波峰基本一致，后期出现差异，原因可能是数值模拟与实验装置边界条件不同。数值模拟中，结构未固定，处于自由边界状态，实验中结构一端固定约束、一端为自由边界。数值模拟和实验结果的对比验证了文中数值模拟螺栓预紧力加载方式的合理性。

图11 数值模拟与实验测点轴向应变曲线对比Fig.11 Axial strain comparison between numerical simulation and experimental results

表6 数值模拟与实验测点波宽及波峰值对比Tab.6 Pulse width and pulse peak comparison between numerical simulation and experimental results

5 结论

通过对截锥和圆筒上测点轴向应变、输入杆中部轴向应力、螺栓应力、螺栓变形及被拉断的最小撞击速度的综合分析可知，螺栓达到断裂或塑性变形时，由撞击产生的拉伸变形远大于预紧力，此时预紧力的影响可以忽略；螺栓在弹性变形时，由撞击产生的拉伸变形与预紧力变形程度接近，故此时预紧力的影响不可忽略。具体结论如下：

1）入射波幅值为975、390 MPa时，螺栓预紧力对反射波的影响不大，对透射波有一定的影响；入射波幅值为13.5 MPa时，螺栓预紧力对反射波和透射波都有一定的影响。

2）螺栓预紧力影响撞击过程中螺栓应力的增加幅值，预紧力越大，螺栓应力增加幅值越小。入射波幅值为975、390 MPa时，预紧力不影响其最大应力；入射波幅值为13.5 MPa时，预紧力影响其最大应力，且预紧力越大，螺栓应力峰值越大。

3）入射波幅值为390 MPa时，预紧力对螺栓最大塑性变形的影响不大；入射波幅值为13.5 MPa时，预紧力对螺栓最大等效变形的影响较大，且预紧力越大，其变形越大。

4）预紧力对螺栓断裂的影响不大。

5）数值模拟与实验的测点轴向应变基本一致，验证了数值模拟中螺栓预紧力加载方式的合理性。