基于ANFIS的磷酸铁锂电池循环寿命预测方法

2021-06-03汤建林彭发豫

电源技术 2021年5期

张宁，汤建林，彭发豫，李剑

(1.海军工程大学兵器工程学院，湖北武汉 430033；2.解放军91024 部队，广东江门 529000；3.解放军92840 部队，山东青岛 266405)

锂离子电池由于具有较高的比能量、比功率，常被广泛应用于汽车、飞行器、水下航行器等载体的动力系统中[1]。磷酸铁锂电池由于具有较好的安全性、大容量、长循环寿命等特点，更加受到关注。但是，锂离子电池在循环使用过程中的容量衰减现象常常会导致电池难以满足任务的要求，甚至会严重威胁设备的安全[2]，所以准确预测电池循环寿命对使用安全性有重要的意义。水下航行器用锂电池组做动力供能装置，由于搁置或使用可能导致电池组容量衰减，再次使用时需要预估锂电池组剩余有效使用次数，这对电动水下航行器安全工作十分关键[3]。电池剩余循环寿命的模型是预测剩余寿命性能精度的重要因素[4]。直接建立电池循环寿命的衰退模型是困难的，因为循环过程中的容量衰减现象发生在电池内部，是电池内部多种反应共同作用导致的不可逆变化，如固体电解质层的形成，析锂现象的发生等，电池内部反应是一个复杂系统。

目前对电池循环寿命的预测主要是基于模型和基于数据驱动的方法[5]。基于模型的预测方法需要对电池内阻等参数进行测量，难以在实际中使用。数据驱动方法利用电池历史数据的有效挖掘并构建输入与输出参数之间关系，具有实用性。数据驱动方法不需要建立电池内部特征变化的关系，以获取的数据来分析电池隐含的变化规律[6]。

自适应神经模糊逻辑系统(adaptive network-based fuzzy inference system，ANFIS)作为目前模拟复杂系统的数据驱动方法用来对电池寿命进行预测。同时考虑到温度变化对锂电池容量的影响[7]，相对以往只研究循环次数与容量的关系，本文将不同温度对容量的影响作为神经模糊逻辑系统输入之一。电池内部变化视为黑箱，通过采用神经模糊逻辑系统对电池循环寿命变化的历史数据进行学习，建立以循环次数、温度、电池容量为输入，相邻循环电池容量差值为输出的电池容量变化模型。用电池容量变化数据构建寿命趋势曲线，从而实现对电池循环寿命的预测。然后将预测数据与实际数据进行对比，验证该方法的有效性。

1 自适应神经模糊系统ANFIS

自适应神经模糊推理系统与常规的模糊推理系统最大的区别就是不需要自己设定推理规则，而是把这一过程交给了计算机。ANFIS 能够对输入集、输出集的模糊化以及推理规则自适应调整，而对于隶属函数的结构和输出函数的结构是不能进行自适应调整的，需要人工设置[8]。自适应神经模糊模型通常分为五层，分别是模糊化层、激励强度层、激励强度归一化层、函数组层、输出层[9]。输入-输出模型结构如图1所示。

图1 神经模糊逻辑结构图

第一层是模糊化层，该层的主要功能是对输入参数进行模糊化处理。图1 中的A、B、C 是模糊集，对隶属函数的参数进行调整，确定输入与每个模糊概念的隶属度，其中隶属函数的参数被称为前提参数。第二层激励强度层通过对输入之间的推理规则强度进行确定，该层的计算一般通过代数积的方式，即将不同输入的不同概念模糊隶属度相乘得到。第三层激励强度归一化层，顾名思义就是将第二层的结果进行归一化处理。第四层是函数组层，该层的每一个节点都对应一个函数，节点的数量是不同输入模糊概念的个数。第五层是输出层，是将第四层函数组层的结果进行加权累加，得到最终结果。

ANFIS 中的Sugeno 结构是ANFIS 的关键部分[10]，其主要是将输出表现为输入变量的线性组合，其数学表达为：

式中：x、y、z为输入；Ai、Bi、Ci为模糊集的输入语言值；pi、qi、gi为权值大小；ri为第二层计算参数；wi为权值；h为输出结果。

自适应神经模糊推理系统主要需要学习隶属函数参数(前提参数)和线性函数组参数(结论参数)这两个参数，结论参数归属第四层。自适应神经模糊学习过程有两种方法，分别是误差逆向传播算法和自适应与最小二乘法相结合的混合学习方法[11]。混合学习方法要先学习结论参数，然后学习前提参数，将输入信号传导到第四层，在保持前提参数不变情况下，通过最小二乘法对结论参数进行学习，完成学习后将信号传播至第五层。误差逆向传播算法要在保持结论参数不变条件下对前提参数进行学习[12]。

自适应神经模糊推理系统对锂电池进行循环寿命预测的算法选用神经网络和最小二乘法的混合算法。锂电池训练数据的输入为Vk，目标向量为Dk，训练数据输入为Vk时输出向量为Qk，输入与输出之间的权系数为rji。

式中：m为输入数据类型的个数；n为输出数据类型的个数。

通过训练学习是为了使Qk趋向于Dk，就是通过改变网络的权系数rji，让Qk趋近或者等于Dk，学习过程中的误差为e。算法训练学习中为使误差尽可能的小，需要多次迭代训练，训练过程中通过如下公式完善输入到输出的权系数，降低输出与目标间的误差，提高预测精度。

式中：l为迭代次数；η1为学习速率；a1为动力常数。

2 电池循环寿命模型训练及建立

2.1 模型输入输出选择

为了消除不同电池容量差异造成的影响，首先对电池数据进行归一化处理。模型使用的数据是不同温度下电池工作数据，温度可作为输入变量。电池循环寿命预测需要确定电池已完成的循环次数，循环次数与电池容量退化程度相关联。循环次数、容量衰减速率和温度作为输入，循环后容量退化差值为输出建立模型。

磷酸铁锂电池寿命预测流程见图2。输入和输出的模糊集都需要进行模糊化。本文设置输入模糊度数量为3。共有27 条逻辑规则，输出集有27 个模糊度。

图2 电池寿命预测方法

2.2 预测模型建立

经神经模糊系统处理后，模型输出为相邻两次循环后容量差值。将相邻循环容量差值和电池循环容量剩余量作为下次计算的输入进行更新。

采用anfisedit 建模工具建立电池循环寿命预测模型。建模有五个步骤，第一步输入电池循环寿命数据训练集；第二步对输入模糊集进行模糊化，并选择模糊集的隶属函数，隶属函数有11 种，选取合适的隶属函数非常重要[13]，隶属函数选择的页面截图见图3；第三步按照输入的模糊集生成“3 输入1 输出”神经模糊逻辑系统网络并确定模糊神经网络输入输出规则，输入输出逻辑规则页面截图见图4；第四步设定训练阈值、训练次数，并将电池数据录入一个四列向量中进行训练[14]，得到隶属函数参数和网络参数值，输入输出的网络结构页面截图见图5；第五步将得到预测结果进行测试。图6为模糊规则观察窗页面截图。

图3 输入输出设定

图4 输入输出之间的逻辑规则

图5 输入输出的网络结构

图6 模糊规则观察窗

应用神经模糊系统对锂电池进行寿命预测，寿命预测误差的大小主要取决于模糊度数量和隶属函数形状[15]。本文预测对每个输入设置3 个模糊度，并选用合适的隶属函数。与设置2 个模糊度的寿命预测相比将大幅降低预测误差。

3 实验验证及数据分析

实验用圆柱体磷酸铁锂单体电池标称容量45 Ah，工作电压2.5～3.7 V，标称循环寿命500 次。电池在30、35、40 ℃下进行充放电循环。

30 ℃循环充放电，电池初始容量43.40 Ah，实验充放电循环累计500 次后容量衰减到初始容量的83.88%；35 ℃循环充放电，电池初始容量45.45 Ah，实验充放电循环累计488 次后容量衰减到初始容量的79.95%；40 ℃循环充放电，电池初始容量42.90 Ah，实验充放电循环累计493 次后容量衰减到初始容量的80.67%。电池退化曲线如图7 所示，已经对数据进行了归一化处理。

图7 磷酸铁锂电池容量退化曲线

以30 和40 ℃条件下电池放电循环数据为训练集，用训练后建立的模型去预测35 ℃条件下预测起始周数后电池寿命。当35 ℃磷酸铁锂电池容量衰减到80%时，预测循环481次。训练数据集超过1 000 个点。

以30 ℃、40 ℃的循环数据和预测起始周数以前35 ℃循环数据为基础，将循环周数、容量衰减百分比、温度作为输入，每循环一次容量衰减值为输出，训练后得到相应模型。用此模型分别预测起始周数为100、200、300 和400 次以后的剩余寿命。

对ANFIS 分别设置模糊度为2 和3 预测锂电池循环寿命，发现3 模糊度的预测数据精度更高。3 模糊度寿命预测见图8。

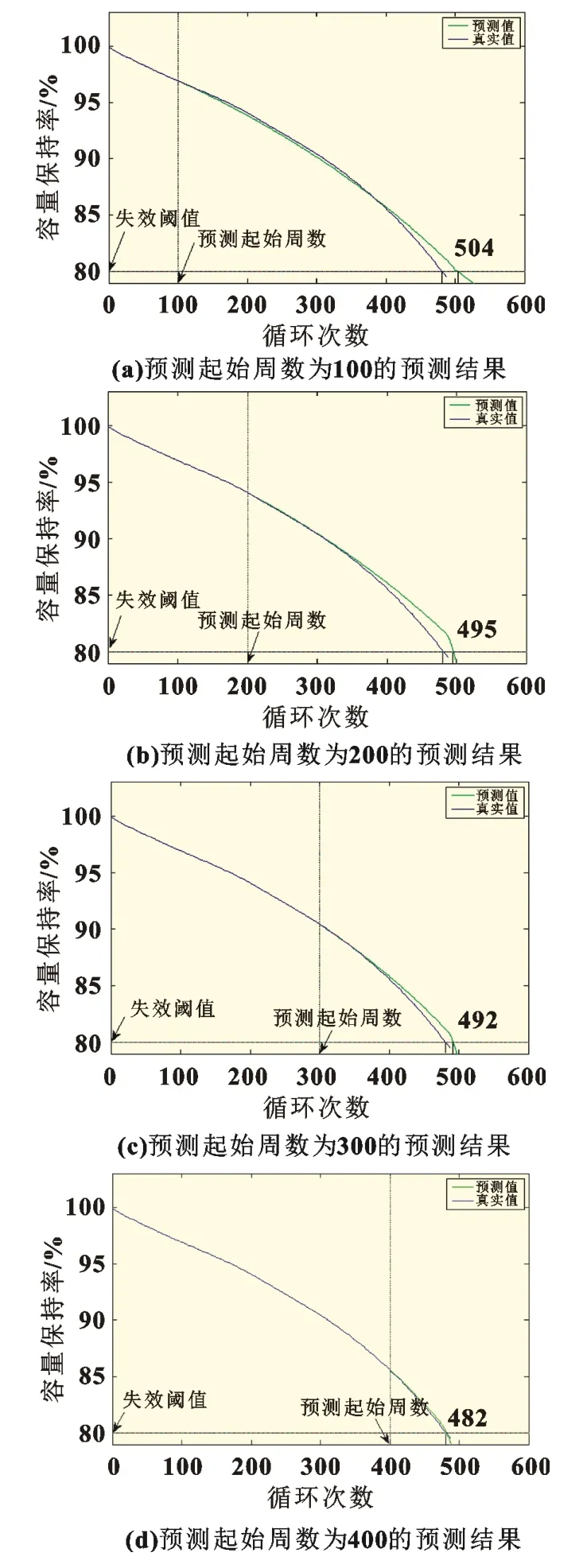
图8 磷酸铁锂电池寿命预测结果

图8(a)中，当预测起始周数为100 时，预测寿命数据为504 次，与实际相差(Err A)为23 次，误差百分比(Err R)为4.78%。对预测结果的统计见表1。

表1 磷酸铁锂电池预测寿命结果

预测数据结果表明ANFIS 方法误差小、可行有效。不同温度条件下磷酸铁锂电池循环数据衰退趋势较平缓。电池寿命早期到晚期，电池容量的衰减速率会有一个从小到大的变化过程，ANFIS 能够很好地学习这些趋势。将预测起点前的电池数据作为模糊神经网络的训练集，是因为每个单体电池会有不同，预测起点前的数据包含预测锂电池实际使用过程中的微弱变化，可以使预测相对准确。设置3 个模糊度并合理设置隶属函数类型要比2 个模糊度的预测结果更精准。