一种基于模型预测的永磁同步电机直接转矩控制策略*

杜承东，聂子玲，李忠瑞

(1.海装驻上海地区第二军事代表室,上海 200129；2.海军工程大学 舰船综合电力技术国防科技重点实验室,湖北 武汉 430033)

0 引 言

永磁同步电机(PMSM)将永磁材料用于转子中，结构简单，体积小，转矩密度、功率密度、效率和可靠性高[1-2]。随着永磁材料性能的提高和技术的进步，PMSM的应用越来越广泛。

直接转矩控制(DTC)是一种典型的高性能交流变频调速技术。DTC通过实时检测电机定子电压和电流，计算磁链和转矩的幅值，并分别与磁链和转矩的给定值比较，利用所得差值来控制定子磁链和电磁转矩，并由磁链和转矩滞环控制器直接输出所需的空间电压矢量，从而达到直接控制磁链和转矩的目的[3-4]。DTC技术结构简单，不需要通过定子电流控制电机，而是直接对转矩进行控制，从而可以实现转矩的快速响应，并且不需要单独的PWM调制器，因此在电机控制领域得到了广泛应用。

如前所述，传统DTC采用2个滞环控制器来实现对磁链和转矩的控制，响应快速，鲁棒性强，但是由于滞环控制器本身的特性，电压矢量切换时间不固定，导致逆变器开关频率不恒定。虽然可以运用空间电压矢量调制方法使逆变器开关频率恒定，但是又会导致电压矢量切换点受限于滞环宽度，引入较大的磁链脉动和转矩脉动，引起高频噪声。为了解决传统DTC存在的问题，将模型预测控制(MPC)应用在DTC系统中，电压矢量切换表可以在线优化，以满足更高的控制要求和实现更多的控制目标。MPC基本思想是基于系统预测模型，计算系统未来特性，从备选变量集合中选择最优变量。因此，将MPC应用于PMSM DTC系统以减小磁链脉动和转矩脉动已成为研究热点。文献[5]提出一种基于连续有限控制集的模型预测直接转矩控制(MPDTC)，采用快速梯度搜索算法降低磁链和转矩脉动，但是控制精度不易工程实现。文献[6-7]提出一种虚拟电压矢量的策略，通过引入更多的虚拟电压矢量来降低磁链和转矩脉动，但虚拟电压矢量的引入又导致控制复杂。文献[8]采用无差拍控制预测电压矢量，最优电压矢量的选择取决于相邻2个非零电压矢量和零电压矢量，降低了运算量，但是无法有效降低定子磁链和电磁转矩脉动。文献[9]提出一种基于卷积神经网络和DTC的模型预测转矩控制策略，有效降低了磁链和转矩脉动。

本文提出了一种新型MPDTC策略。该策略基于模型预测算法，继承了传统DTC的滞环控制器，在滞环控制器允许的误差范围内控制定子磁链和电磁转矩。同时,通过在线优化改进传统DTC的电压矢量切换表，预测电压矢量作用下的定子磁链和电磁转矩的轨迹，并采用代价函数最优的方法实现对系统性能目标的控制。对提出的MPDTC策略进行了试验验证，试验结果验证了该方法的可行性和有效性。

1 PMSM驱动系统

1.1 PMSM数学模型

假设内置式PMSM为理想电机，且满足以下条件[10]：

(1)忽略电机铁心的饱和；

(2)不计电机中的涡流和磁滞损耗；

(3)电机中的电流为对称的三相正弦波电流。

内置式PMSM在两相旋转坐标系下的数学模型如下[11]。

定子电压方程:

(1)

定子磁链方程:

(2)

电磁转矩方程:

(3)

式中：ud、uq分别为定子电压的d、q轴分量；Rs为定子电阻；id、iq分别为定子电流的d、q轴分量；ψd、ψq分别为定子磁链的d、q轴分量；ωr为转子角速度；Ld、Lq分别为d、q轴电感分量；ψf为转子永磁体磁链；Te为电机的电磁转矩；p为电机的极对数。

1.2 两电平三相电压源逆变器

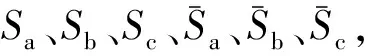
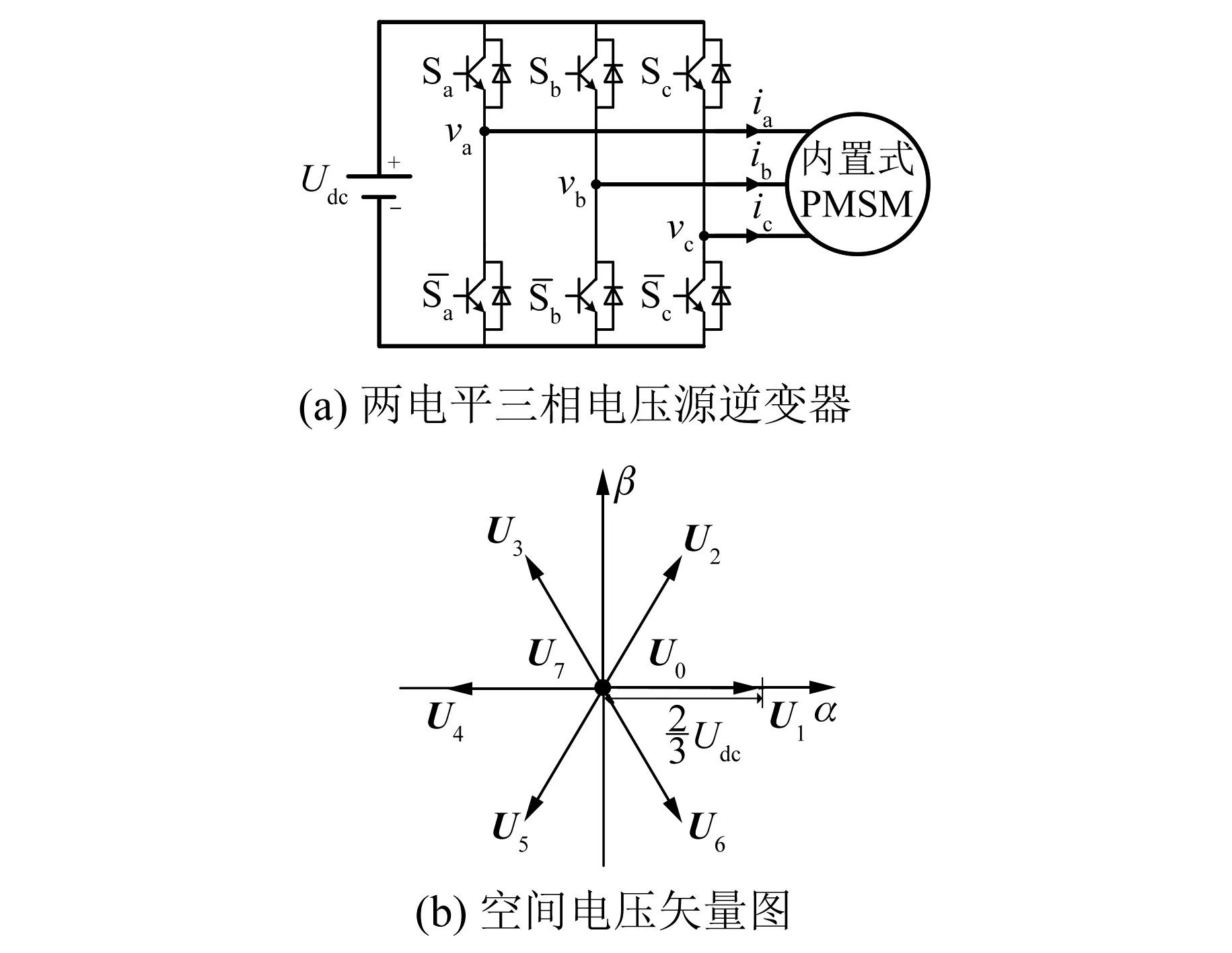
图1 三相电压源逆变器原理图和空间电压矢量图

(4)

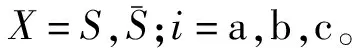
定义两电平三相电压源逆变器的开关状态组合为(SaSbSc)，由式(4)可知，逆变器共有8种开关组态，对应8个基本电压矢量，包括6个有效矢量U1～U6和2个零矢量U0、U7,如图1(b)所示。

逆变器输出电压矢量可表示为

(5)

2 传统DTC策略

2.1 传统DTC系统框图

传统DTC系统框图如图2所示，主要由PMSM、两电平三相电压源逆变器。磁链和转矩观测器、滞环控制器、开关表选择模块等组成。

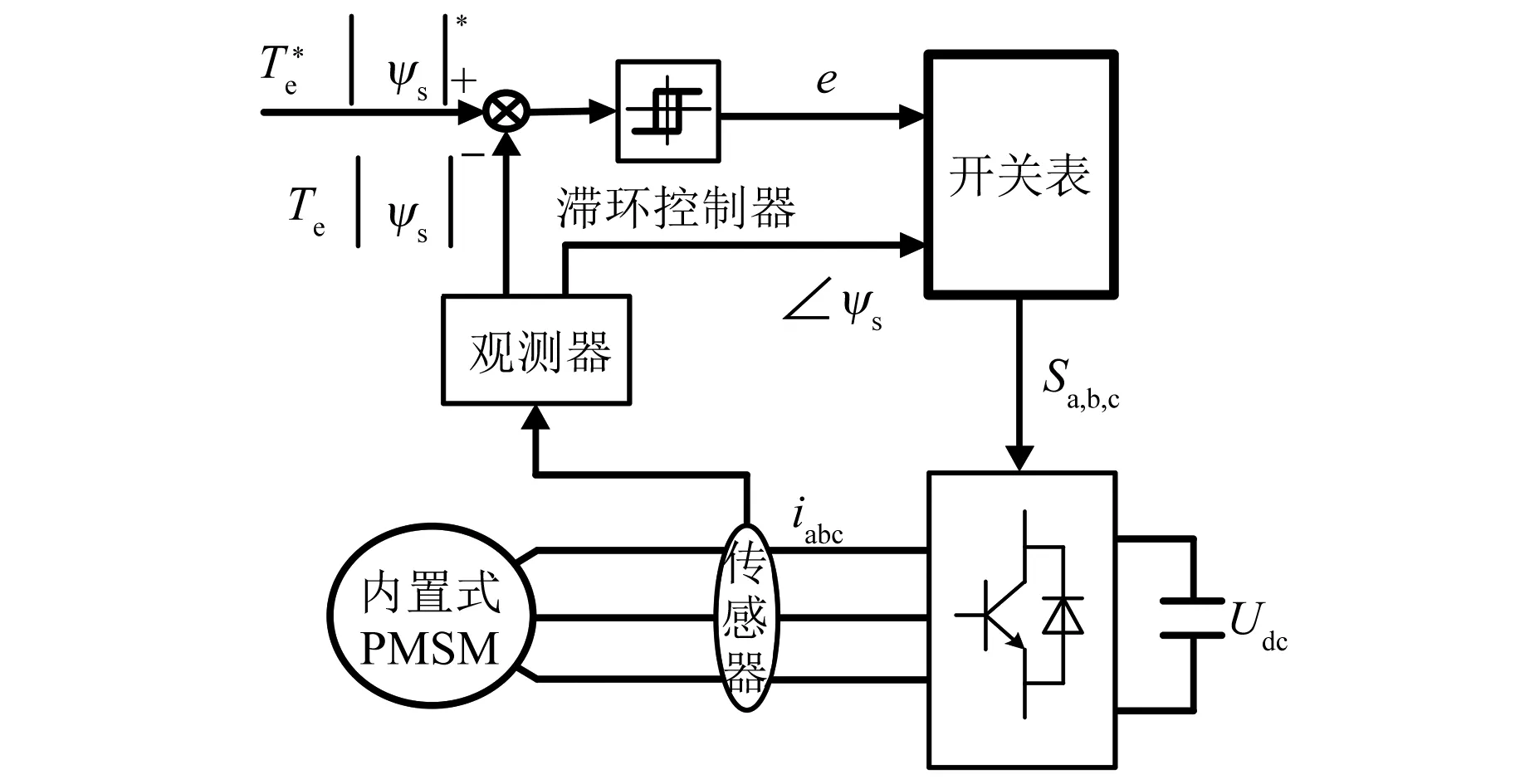
图2 传统DTC系统框图

传统DTC通过将定子磁链幅值和电磁转矩的给定值分别与定子磁链幅值和电磁转矩的观测值比较，产生的差值分别输入磁链滞环控制器和转矩滞环控制器，通过滞环控制器的输出状态并结合定子磁链相角来选择电压矢量，生成PWM信号，对逆变器的开关状态进行最佳控制，从而实现对转矩的直接控制。

2.2 传统DTC滞环控制器

2.2.1 模拟滞环控制器

模拟方式下的滞环控制器，其工作原理是根据电机特性，给定输入变量并设置好滞环宽度后，在输入变量的变化范围未超过滞环宽度时，控制器的输出状态不会发生变化，从而保持施加在逆变器上的电压矢量不变。这种方式的电压矢量切换时间不固定，逆变器开关频率不恒定，难以精确控制。

模拟方式下的转矩滞环控制器及原理如图3所示。

图3 模拟转矩滞环控制

2.2.2 数字滞环控制器

滞环控制器的数字方式采用固定的控制周期，从而保证逆变器的开关频率恒定。电压矢量的切换始终发生在控制周期结束的时刻，切换所需的周期数取决于滞环宽度以及控制周期。工作在数字方式下的转矩滞环控制示意图及工作原理如图4所示，其中Ts是控制周期。系统的控制性能受滞环宽度和采样率的影响[12]，为了实现与模拟方式相同的控制性能，采样率和开关频率必须很高。

图4 数字转矩滞环控制

3 新型MPDTC策略

3.1 系统框图

为了解决传统DTC存在的磁链和转矩脉动大、逆变器开关频率不恒定等问题，本文提出一种新型MPDTC策略，通过预测可能出现的定子磁链和电磁转矩，直接控制磁链和转矩。新型MPDTC系统框图如图5所示。

图5 新型MPDTC系统框图

新型MPDTC策略采用了滞环控制器和代价函数相结合的新方式。将观测到的电流ik发送到观测和预测模型，结合可能的逆变器电压矢量，预测下一控制周期可能出现的电流值ik+1。通过旋转变压器观测内置式PMSM的转子位置，将转子位置信息同样发送到观测和预测模型，结合预测的电流值ik+1，预测下一控制周期可能的定子磁链ψs(k+1)和电磁转矩Te(k+1)。预测量和给定量一起发送到滞环控制和代价函数优化模块。代价函数优化可以考虑多个电机控制目标，追求控制目标的最优化。基于滞环控制器和代价函数优化模块，下一控制周期的最优电压矢量可以被筛选出来。

3.2 新型MPDTC策略实现方式

基于磁滞控制器和代价函数优化部分，可以获得逆变器最优电压矢量。图6(a)所示为新型MPDTC转矩滞环控制示意图。

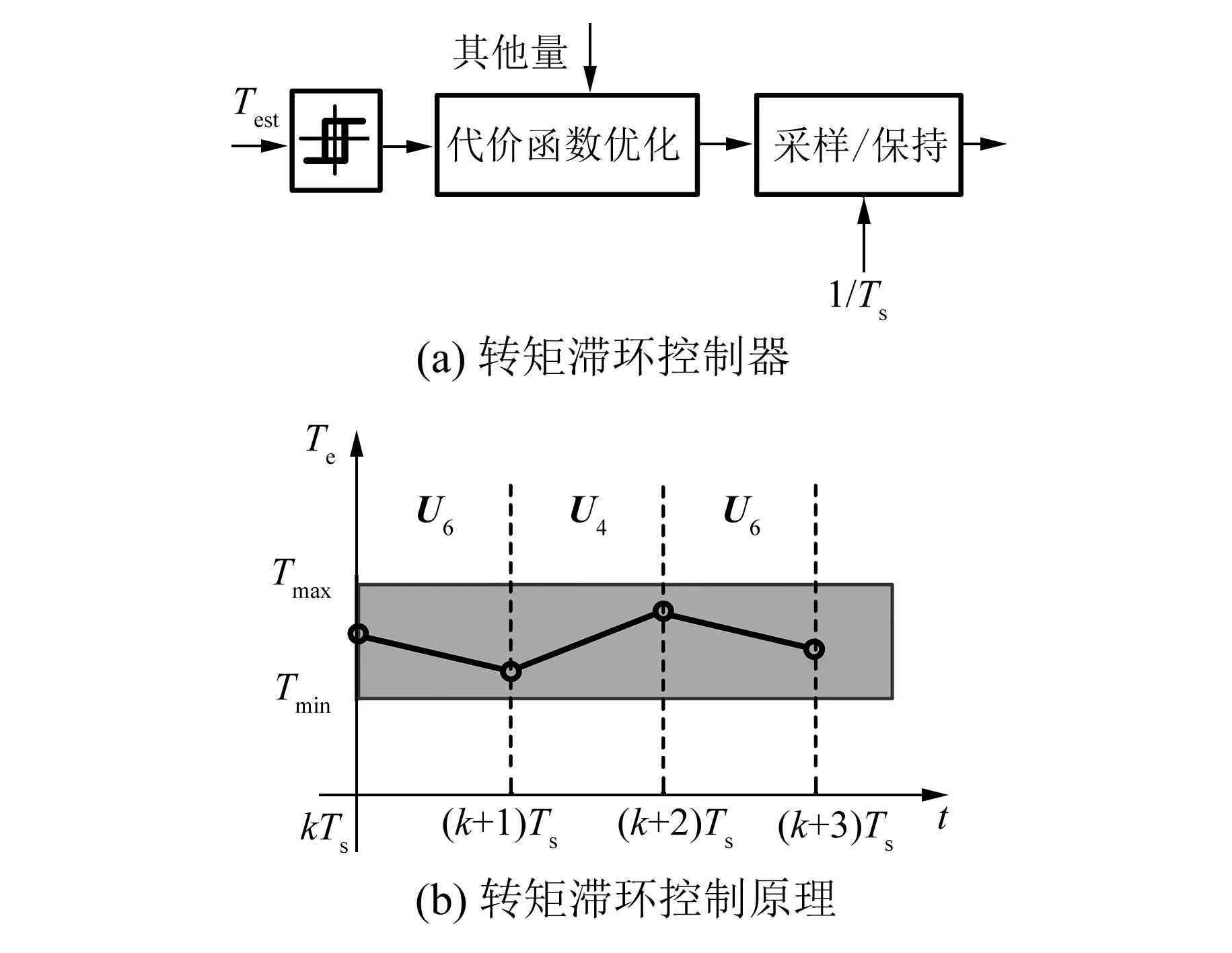
图6 新型MPDTC转矩滞环控制

其中，代价函数优化模块基本原理如下：

(6)

式中：g为代价函数；K1、K2、K3为权重系数；f(i)为电流保护函数。

新型MPDTC滞环控制原理如图6(b)所示。在每个控制周期Ts，逆变器电压矢量始终保持不变，并且一个电压矢量只保持一个周期。在第k个周期内，电压矢量始终保持U6，在该周期结束时刻也即第k+1周期开始的时刻，根据模型预测的方法，由滞环控制器和代价函数优化模块决定新的电压矢量，在第k+1周期内新的电压矢量是U4。这种工作方式下，与图4不同，电磁转矩始终在滞环宽度内，转矩脉动较小，可保证滞环宽度不至于过大，提高了滞环控制特性。当然，除了电磁转矩这一控制特性外，电机的其他控制特性也可采用这种方式。

新型MPDTC实现的流程图如图7所示。基于电机模型，所有可能的逆变器电压矢量全部用于获取预测量，包括磁链和转矩预测量，进而分2步选择出最优的电压矢量。第1步为滞环控制。将磁链预测和转矩预测分别送入相应的滞环控制器，以选择逆变器电压矢量，并确保磁链预测和转矩预测分别在各自的滞环宽度内。第2步为代价函数优化。考虑不同的控制目标，根据滞环控制器的输出选择最优的电压矢量。如果滞环宽度较大，滞环控制器输出的电压矢量数量可能大于1；同样地，如果滞环宽度较小，滞环控制器输出的电压矢量数量可能为0。如果被选电压矢量的数量大于1，则将被选电压矢量送入代价函数优化模块获得最优逆变器电压矢量。如果被选电压矢量的数量等于1，则将该被选电压矢量视为最优电压矢量。如果被选电压矢量的数量等于0，则将所有可能的电压矢量送入代价函数优化模块，最优电压矢量将根据磁链和转矩的控制以及其他控制目标进行选择。事实上，如果滞环控制器的滞环宽度合适，被选电压矢量的数量将大于0。

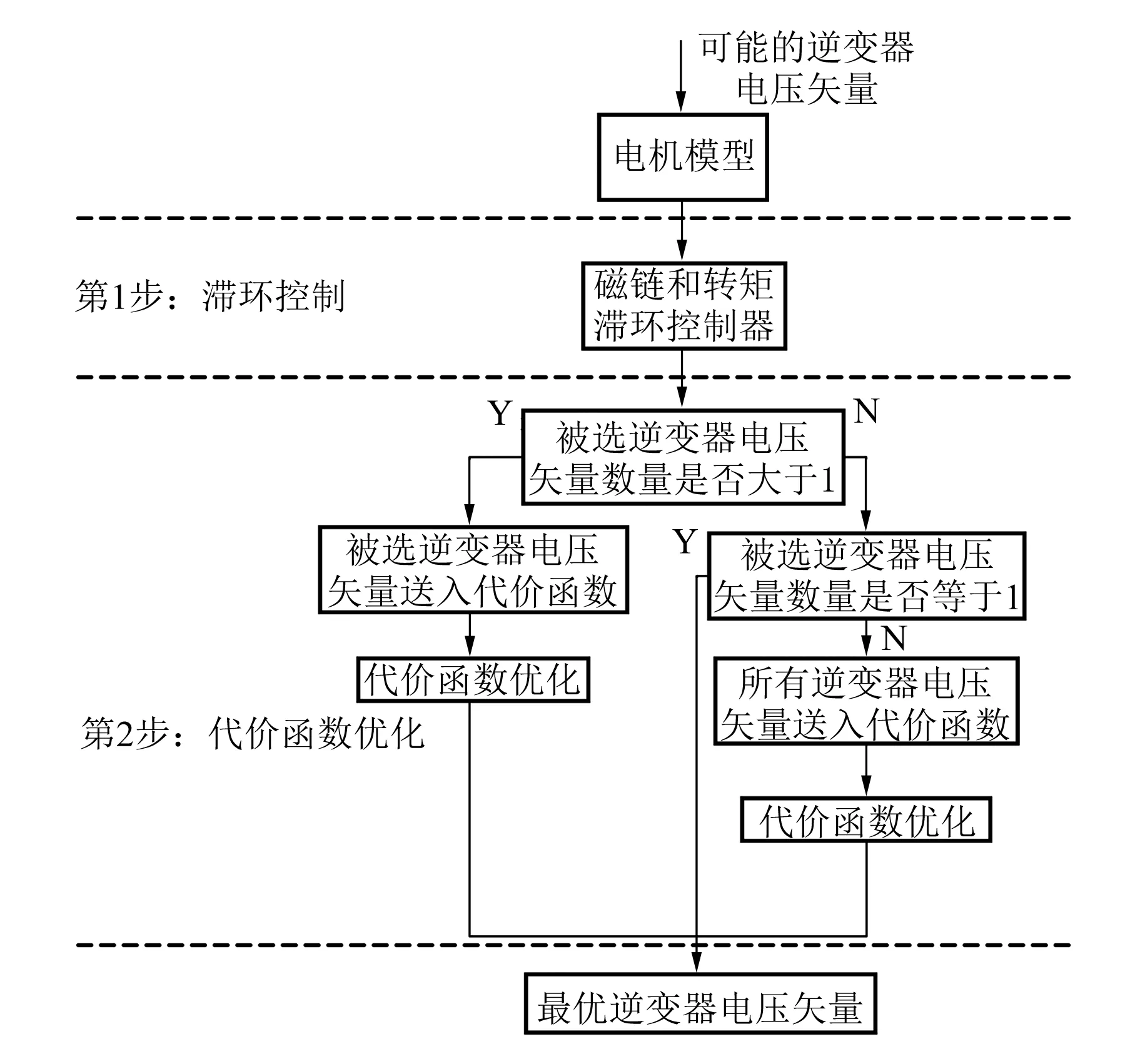
图7 新型MPDTC流程图

4 试验验证

为验证所提MPDTC策略的有效性，在一台凸极PMSM驱动平台上对所提出的控制策略进行了试验验证，并对试验结果进行了分析。试验用电机参数如表1所示。

表1 电机主要参数

图8给出了在所提出的MPDTC策略下电机电磁转矩稳态性能图，给定转矩为10 N·m。从图8可以看出，实际转矩值稳定在9.5～10.5 N·m的范围内，并且更多的转矩值在10 N·m附近，说明在该控制策略下，可以在不超过滞环宽度的前提下对逆变器空间电压矢量进行代价函数优化，选出最优电压矢量，保证了合适的滞环宽度，减小了磁链和转矩的脉动。

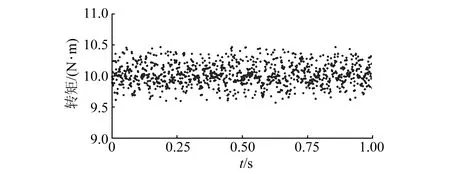
图8 电机电磁转矩稳态性能图

在对所提出的MPDTC策略下电机电磁转矩的稳态性能进行试验验证后，进一步对电机电磁转矩的动态响应进行分析。图9给出了在所提出的MPDTC控制策略下电机电磁转矩动态响应图，给定转矩由2 N·m突变为10 N·m。从图9可以看出，在给定转矩发生突变时，该控制策略动态响应快，无振荡和超调，动态性能好。

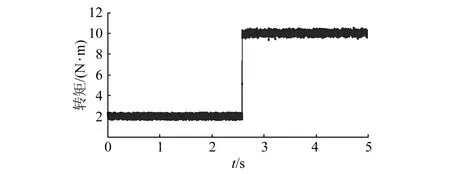
图9 电机电磁转矩动态响应图

5 结 语

本文提出了一种新型的MPDTC策略，可以在不超过滞环宽度的前提下获得代价函数最优的电压矢量，保证了合适的滞环宽度，减小了磁链和转矩的脉动，防止出现过大的电流值，保护功率开关器件。通过PMSM驱动平台对所提出的控制策略进行了试验验证。试验结果表明，新的MPDTC策略能够将滞环宽度控制在合理范围内，对电机的磁链和转矩脉动具有良好的抑制效果，而且具有良好的快速动态响应性能。