四川人寿新投保的SPSS数据分析报告
2021-06-03四川大学锦城学院计算机与软件学院
四川大学锦城学院计算机与软件学院 向 倩 杨 杉
在获取的新投保数据中包括机构、险种、投保时间、缴费方式、缴费期限、投保份数、总保费、保额、客户号、性别、年龄、婚姻状况、过去三年收入、教育程度、职业以及家庭人口;针对不同婚姻状况与保额的关系、不同年龄与保额的关系、总保费与保额之间的关系、性别与过去三年的收入的关系,采用了排序、分组、单因素方差分析、简单相关分析以及探索分析,得到总保费与保额之间是显著相关的、男性的过去三年平均年收入高于女性、婚姻状况与保额有显著关系、保额均值有显著的差异。
在全面建成小康社会、加快步入社会主义现代化的关键时期,保险业作为金融体系的重要一员,合理评估其现代化进程、科学度量其发展水平、总结其发展成绩是社会各界关注的焦点。
随着中国经济近年来的高速发展,居民收入提高和保险意识的增强,民众对于保险产品的保障与投资功能需求日益旺盛,进而释放了大量商业保险,特别是商业健康保险的市场需求。尤其是2020年,新冠肺炎疫情在全球范围内的大肆蔓延,令我国居民健康保障意识得到了明显的提升,也让国内的商业健康保险获得了爆发式增长。在近年来政策利好逐步释放、市场需求快速增长、产业融合和科技赋能加速等多重机遇的叠加下保险业进入高质量发展轨道,其风险保障和经济补偿作用得到更加充分的发挥,保险业在解决养老、居民健康等民生问题上发挥出了更加重要的作用。然而保险公司层出不穷,与此同时,保险企业是否能长期留住客户的问题也成为保险公司发展的一大重点,以服务质量为基础的留客和锁客已成为保险公司的获益前提。因此人们对保险的购买和保险公司的保险种类以及质量都有了一定的要求。
1 分析思路
基于越来越多人不能买到适合自己的保险,让自己的利益最大化,保险公司的定制方案也不能“一呼百应”的背景下,通过四川人寿保险公司的新投保数据,一共有机构、险种、投保时间、缴费方式、缴费期限、投保份数、总保费、保额、客户号、性别、年龄、婚姻状况、过去三年平均年收入、教育程度、职业、家庭人口这十六列数据排序、分组、单因素方差分析、简单相关分析以及探索分析的方法,对不同婚姻状况与保额的关系、不同年龄与保额的关系、总保费与保额之间的关系、性别与过去三年的收入的关系进行了分析,通过分析客户购买保险的情况,优化保险公司的保险种类和保费,让客户根据自己的实际情况选择。
2 数据说明
2.1 数据来源
数据来源于四川人寿保险公司,覆盖了某段时间内客户新投保的数据,数据表中包含了机构、险种、投保时间、缴费方式、缴费期限、投保份数、总保费、保额、客户号、性别、年龄、婚姻状况、过去三年平均年收入、教育程度、职业、家庭人口16个字段共90多万条数据,64M。
2.2 数据清洗
将四张数据表中带有空值的数据整行删去并且由于数据分析的缘故将新投保数据中过去三年平均年收入为0的数据整行删除,其操作步骤为在“开始”菜单栏中,点击打开“查找”对话框,在“查找内容”中输入“0”;选择“单元格匹配”前面的复选框,选中所有查找结果。在查找结果区域中按下“Ctrl+A”键,选中所有的查找结果,然后点击右键删除0值所在的行。将无用数据列投保时间、投保份数、教育程度、家庭人数删去,针对剩下的数据进行分析。
3 数据分析
3.1 总保费与保额之间的关系
针对总保费与保额之间的关系,采用了简单相关分析方法;
在分析选项卡中选中相关选项,打开相关选项中的双变量分析,将总保费和保额添加到变量中,选中Pearson和双侧检验,最后生成相关系数表(表1)。
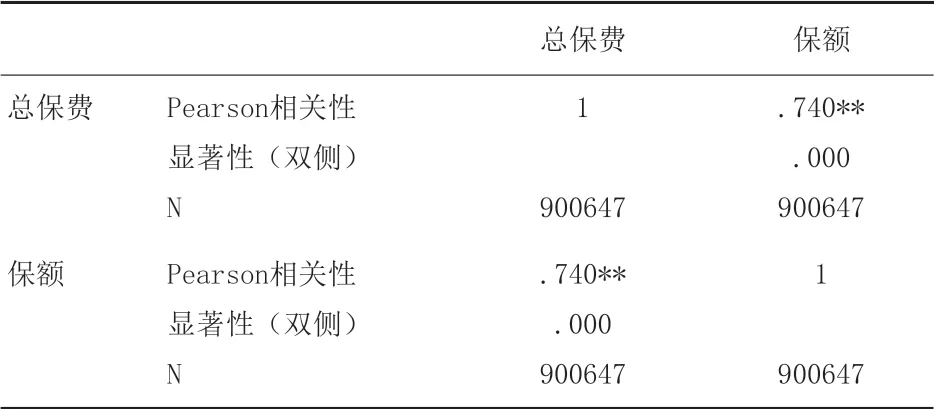
表1 相关性分析结果
可以看出总保费与保额的双侧检验值为0,是小于α=0.01的,应该拒绝原假设,还可以清晰看到总保费与保额之间是显著相关的,其相关系数为0.74。
3.2 性别与过去三年平均年收入的关系
针对性别与过去三年的收入,采用了探索分析方法在分析选项卡中选中描述统计,打开描述统计中的探索功能,将过去三年平均年收入放在因变量列表中,将性别放入因子列表中,最终输出性别与过去三年平均年收入的描述统计(表2)。
男性和女性的偏度和峰度都为正值,为右偏以及尖峰分布,右偏说明右边的分布密度稀疏,也就意味着高工资的人相对较少,尖峰意味着挨着平均工资的人比较集中,并且男性的平均值、偏度、峰度都高于女性,说明男性过去三年平均年收入高于女性。
3.3 不同婚姻状况与保额的关系
针对不同婚姻与保额的关系,采用了排序和单因素方差分析;
在数据选项卡中打开排序个案,将婚姻状况添加到排序依据中,对婚姻状况进行重新编码,将婚姻情况进行标记,D-0、S-1、M-2、X-3、W-4、R-5,然后打开单因素方差分析选项,进行两两对比,最后输出多重对比表(如表3、表4、表5所示)。
3.4 不同年龄与保额的关系
针对不同年龄与保额的关系,采用了排序和单因素方差分析;
在数据选项卡中打开排序个案,将年龄添加到排序依据中,对不同年龄进行重新编码,将年龄进行标记,分为0-18为0、19-38为1、39-58为2、58以上为3,然后打开单因素方差分析选项,进行两两对比,最后输出多重对比表(如表6~表9所示)。
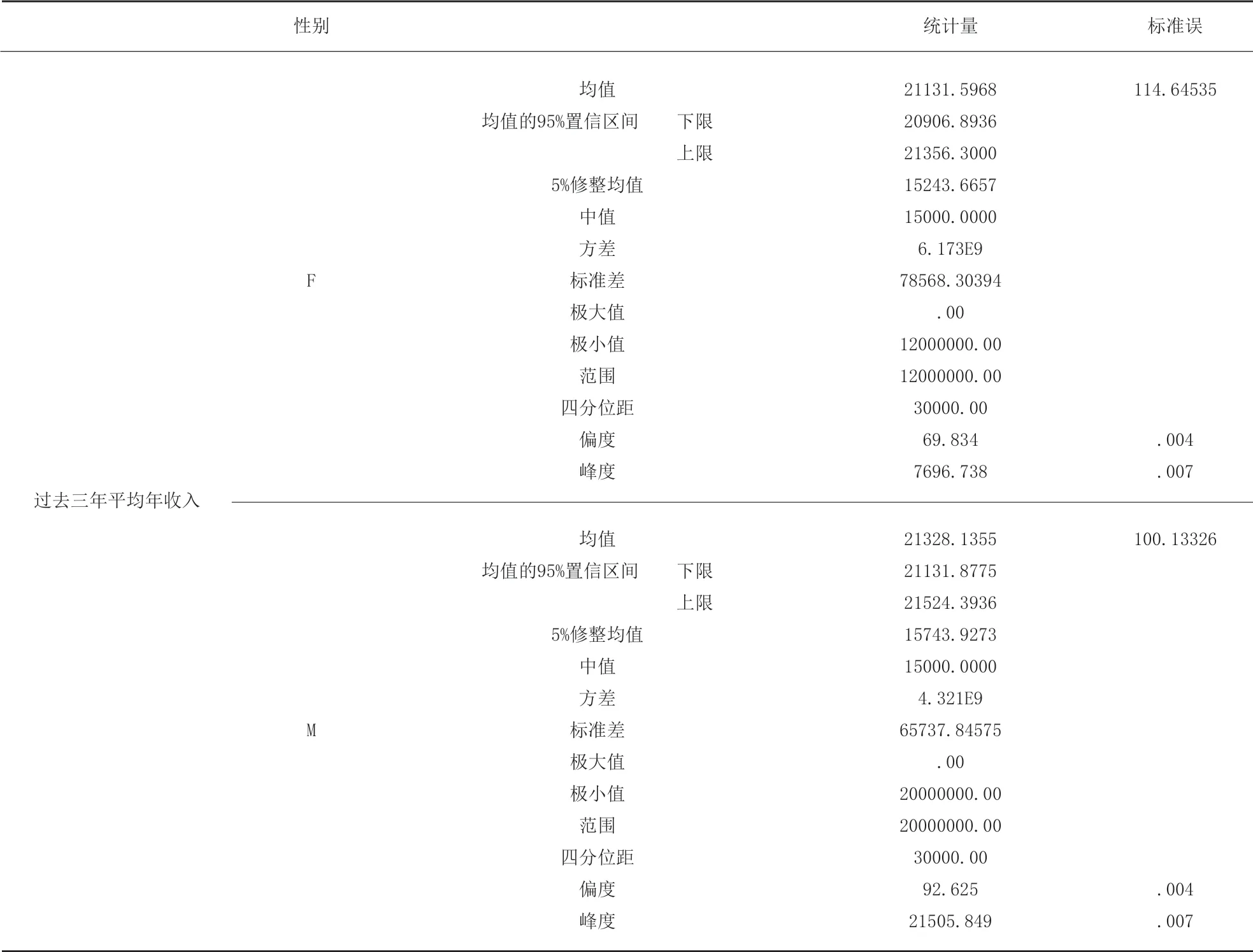
表2 数据描述

表3 方差齐性检验

表4 对比检验

表5 多重比较分析结果因变量:保额
方差不具有齐次性,分析Tamhane表。
D与S、M、X、W有显著差异,与R无显著差异;S与X、W有显著差异,与M、R无显著差异;M与X、W有显著差异,与R无显著差异;X与W、R无显著差异;W与R无显著差异;R与任意情况均无显著差异。
D显著高于S、M、X、W;S显著高于X、W;M显著高于X、W;X显著高于W;W不显著高于任意情况;R与其余情况均无显著差异。
离异人群购买保险占大多数,其次是单身人群,丧偶人群投保最少,已婚人群处于中间水平。

表6 方差齐性检验保额
显著性<0.05,说明拒绝原假设,即方差不具有齐次性,仅对Tamhane进行讨论。

表7 ANOVA保额
不同年龄段的保额的均值是否有显著的差异,显著性<0.05,拒绝原假设,说明至少有3个年龄段的平均保额有显著的差异。

表8 多重比较因变量:保额
两两比较,因为方差不具有齐次性,查看Tamhane。
18岁以下年龄段与19-38岁年龄段进行比较,根据显著性列小于0.05,判断18岁以下与19-38岁年龄段有显著差异,根据均值差(I-J)列,18-38岁的保额显著高于18岁以下;18岁以下与39-58岁年龄段进行比较,显著性0.996>0.05,没有显著差异;判断18岁以下与59岁以上年龄段,显著性0.146>0.05,没有显著差异。
19-38岁年龄段与其他年龄段进行比较,显著值均为0<0.05,有显著差异,且根据均值差(I-J)列判断,19-38岁年龄段保额均值高于所有年龄段。
39-58岁年龄段与59岁以上年龄段进行比较,显著值均为0<0.05,有显著差异,且根据均值差(I-J)列判断,39-58岁年龄段保额均值高于59岁以上。

表9 对比检验
方差不具有齐次性,查看不假设等方差的数据,显著性(双侧)为0,拒绝原假设,所以他们的保额均值有显著的差异。
4 结论及建议
4.1 结论
通过使用SPSS对新投保数据进行分析之后得到保额与总保费的关系:总保费越高,其保额越高;对性别与过去三年平均年收入可以得出性别与收入有关系,男性过去三年平均年收入高于女性;对不同婚姻状况与保额关系可得不同的婚姻状况与保额有关系,离异人群购买保险占大多数,其次是单身人群,丧偶人群投保最少,已婚人群处于中间水平;对不同年龄与保额可得不同年龄影响着保额。
4.2 建议
对个人而言,在实际生活中,要根据自身及其家庭的实际情况具体分析。比如自己比较年轻可以选择意外险;如果年龄比较大,这时需要选择重疾险或购买养老保险,并且领取养老保险金对提升老人幸福感有正效用,对中等收入老人有显著正效用。在购买保险时最好先购买家长的,再购买孩子的,不过实际生活中很多人先买孩子的,其实这种方法不可取,毕竟家长才是家庭收入的主要来源,家长得不到保障,家庭的收入也就不能得到保障。
对保险公司而言,保险公司应该针对不同的婚姻状况、不同的年纪、不同的性别有不同的保险方案,比如为还在上学的人购买保险时,可以推荐购买教育险,对于家长来说,为子女购买教育金保险,不但能够在资金充足的情况下,提前筹备好子女的教育基金,同时还能够规避子女完成教育之前的风险,从而确保在家庭遭遇风险以后,子女的教育还能正常进行。对中青年人且有家庭可以推出一些保额相对较高的险种,保证出现意外时得到最大的保障。保险公司应当加快险种的开发和结构的调整,不仅仅要看重客单价格,还应当聚焦需求未得到满足的人群,实现保险产品的差异化,打通养老产业链,加强相关的服务能力,为客户提供更多层次的保险选择。这样可以更大程度的保障买保险的人的利益同时也为自身带来利益。加强保险知识宣传,提高居民保险意识;让更多人购买保险。
