LFM目标回波信号的Duffing振子检测方法

李 楠，杨 阳

（1.东北电力大学信息工程学院，吉林吉林132012；2.大连大学信息工程学院，辽宁大连116622）

0 引 言

主动声呐探测水下目标时，由于工程上对声呐信号参数分辨力的需要，发射的LFM 信号通常是具有大时宽-带宽积的脉冲压缩信号。当声呐发射功率一定，发射信号的频谱由频率调制技术实现扩展。由Parseval 定理可知，频谱扩展会使信号功率谱密度下降。同时，由于目标声散射特性及水声传播特性的作用，以及强混响干扰的存在，使得接收目标回波信号很微弱。目前，常用的LFM 目标回波检测方法有：（1）相关及匹配滤波法[1-3]。该方法是利用接收信号中的目标回波信号与发射信号具有较强相关性，与噪声不相关实现检测与参数估计。当受干扰或背景噪声中包含如混响等色噪声时，检测能力严重锐化甚至失效。（2）时频分析方法。典型方法有短时傅里叶变换（Short-time Fourier Transform，STFT）[4]、小波及同步压缩变换[5-6]、Wigner-ville 分布（Winger-ville Distribution，WVD）[7-9]等时频分析方法，它们的共性是利用核函数的时频聚集性对非平稳信号进行分析。STFT 的核函数时频分辨率固定，无法自适应地调整时频参数跟踪信号，分析复杂信号效果不佳；小波及压缩变换方法虽具有可调的时频分辨率，但小波基函数的选取不同，分析效果也不同，且小波基选取没有统一标准；而基于二次型的WVD时频分析方法在分析多分量信号时不可避免地存在交叉项，交叉项产生干扰使误判率增大。（3）基于分解理论的信号分离方法。典型方法有盲源分离法[10,11]、稀疏分解法[12]、经验模态分解法[13-14]等。盲源分离法是将信号与背景干扰视为不同的源，利用其不相关特性进行分离。但是，当干扰与信号具有一定相关性时，分离效果不佳；稀疏分解法是通过选择过完备原子库作为基函数，对信号进行投影分解，不存在交叉项干扰的问题。但由于过完备原子库中的基函数不再具有正交性及唯一性，选取不同原子库时信号分解成分不唯一，物理意义不明确；经验模态分解法是在定义内禀模态函数基础上，将复杂的多分量信号自适应地分解为若干个IMF 分量及残余分量之和的形式。当干扰信号频带与系统固有频率重叠时其分解效果不佳，并且在分解过程中还存在过包络、欠包络、模态混淆和端点效应等问题。

当主动声纳接收信号的信混比较低，目标回波信号与噪声干扰在时域、频域及时频域有交叠情况下，上述几种方法分离或特征提取效果不佳。而具有典型非线性动力学特性的Duffing振子系统，不受时域、频域及时频域参数影响，具有较强的噪声免疫特性，在低信噪比情况下仍有较好的弱周期信号检测能力。目前，利用Duffing振子检测弱LFM 信号取得了初步的研究成果，文献[15]将LMF解调频后构造Duffing 振子滤波器阵列，利用Lyapunov 指数判别信号是否存在及参数估计。该方法中系统的相态判别方法选用Lyapunov 指数法，结构复杂，算法耗时，且并未将其应用于实际信号的检测。文献[16]将LMF 线性调频信号进行短时处理后，认为在截取的时窗内信号频率是平稳不变的，然后利用Duffing 振子系统检测单频周期信号的方法进行检测，最后通过识别结果重构出时频变化图。该方法对LMF 信号的检测及频率估计是在无噪声干扰情况下实现的，文中未讨论噪声对检测性能的影响。上述两种方法仅从理论及数值仿真层面上对LMF 信号进行检测，且LMF 回波信号信噪比门限值不得低于-10 dB。

本文借助Duffing 振子系统具有较强的弱信号检测能力，首先利用LFM 信号在最佳分数阶傅里叶变换域具有较高的时频聚集性，研究了多亮点LFM 目标回波信号的解调频问题；其次根据亮点模型，理论推导了LFM信号解调频后的信号形式；最后针对解调频后频率未知的单频信号检测问题，提出了基于分数阶傅里叶变换的变频Duffing 振子检测方法。并将该方法对水下沉底及掩埋实测数据进行了分析处理，验证了方法的可行性及有效性，为低信混比下LFM 目标回波信号的检测提供了一个新思路。

1 基于FRFT的LFM回波信号解调频

利用Duffing振子系统实现弱信号检测的基本前提是待测信号为单频信号，而LFM 信号是频率经线性调制形成的宽带信号，不满足Duffing 振子系统检测前提条件。根据LFM 信号在最佳分数阶Fourier变换域的谱分布具有冲激特性，对最佳分数阶Fourier变换谱进行Fourier反变换，将LFM 信号解调频为单频信号，即可利用Duffing振子系统实现LFM信号的检测。

1.1 多亮点LFM回波信号解调频

主动声呐发射幅度为A，初始频率为f0，调频率为k的LFM信号，其表达式为

设水下目标包含N 个几何声散射分量，根据亮点模型，忽略弹性声散射成分，回波信号可表示为

式中，Ai，τi及φi分别为第i个几何亮点的幅度、时延及相位因子。

由式（7）可知，多亮点LFM 回波信号解调频变换后的时域信号为多个单频信号的线性叠加。对第i 个声散射分量，信号的频率及幅值分别为fi=( f0- kτi)/cscα，Ai= Bi/cscα；单频信号数量与几何声散射回波数量一致，频率与时延因子τi及最佳旋转角度α有关。

1.2 解调频信号的频率偏移分析

在最佳分数阶傅里叶变换过程中，已知LFM信号调频率k ＞0，引入量纲归一化因子s=(Td/fs)1/2（Td为信号时宽，fs为采样频率），采样间隔变为1/s，量纲归一化坐标x = t/s,y = fs。经量纲归一化处理后信号的时间区间为[-Td/2s,Td/2s]，离散化后FRFT域u的分辨率为

又由于

变换后频率f的估计误差Δf为

单频信号频率的估计区间为[ f＾- Δf/2,f＾+ Δf/2]，Δf并不是一个定值，它受调频率k、采样频率fs和LFM 信号脉宽Td联合作用。增大采样时间Td，采样频率fs可使变换后单频信号变化范围变小，而增大调频率k则使单频信号变化范围增加。

2 LFM目标回波信号的变频Duffing振子检测方法

LFM 经分数阶傅里叶变换解调频，解调后的单频信号频率受采样时间Td、采样频率fs和采样点数量N 等因素影响，通常为未知量。针对上述问题，本文改进了常规Duffing 振子检测方法，通过改变系统内置策动力的频率，对被测信号中周期分量进行扫描，若二者频率一致，且弱周期信号幅值与系统内置策动力幅值之和大于系统临界值，Duffing振子检测系统发生共振现象，系统相图由混沌态变为大尺度周期态，从而实现弱周期信号的检测。

2.1 变频Duffing振子检测模型

变频Duffing振子检测数学模型为

式中，ω0为周期策动力角频率初值，α=0，1，2，3，…，N，Δω 为频率分辨率，搜索频率步长为αΔω，s(t)为外加驱动力。

通常s(t)由若干单频信号分量及各类干扰nJ(t)和噪声n( t )构成，其表达式为

当ω0+ αΔω = ωi且r + Ai＞rd时（rd为混沌临界值），系统对驱动的响应达到最佳周期共振条件，系统发生相态跃变，实现信号检测及频率捕捉。

2.2 Duffing系统相态的PMCF判别方法

在利用Duffing 振子系统检测弱周期信号时，Duffing 系统的相态判别是检测关键问题之一。本文从实际工程需求出发，提出了一种基于Poincare 映射特征函数（Poincare mapping characteristic function，PMCF）的系统相态定量判别方法。

设Duffing振子系统模型为

引入θ（θ = ωt）变量，系统变为三维自治系统，将式（13）降维后相空间扩展为R2× S1：

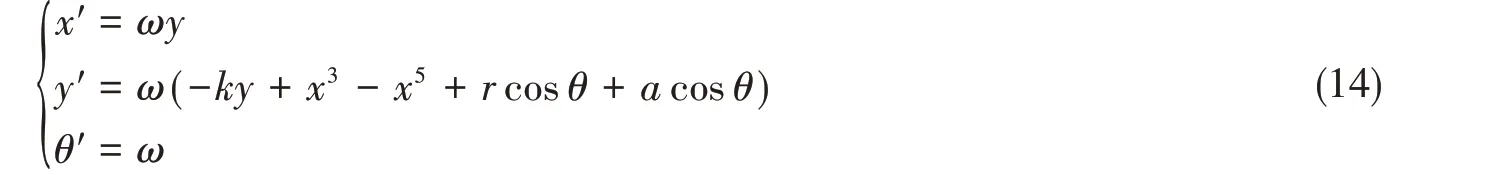
设系统观测量为Z(t) =[x(t) y(t) θ(t)]T，利用构造庞加莱截面的方法对这一观测量重构，获得一个时间延迟的3×(m + 1)维矢量矩阵：

式中，T 为系统内置策动力周期。当选取截面∑={( x,y,θ)|θ = φ} 时，其中0 ≤φ ＜2π，记下z(t)轨道与该截面所有交点d(t) ={(x(tn),y(tn)|θ = φ }，n = 0,1,2,3…，tn为z(t)与截面{θ = φ}第n 次相交的时间。系统观测数据经过延迟重构和Poincare 截面切割后获得的Poincare 映射，将原动力系统所决定的随时间连续运动转变为在Poincare截面上离散的映射。图1为大尺度周期态及混沌态时，Duffing系统观测量经Poincare截面（φ = π/2）切割后系统变量xn、yn的Poincare映射时序图。从图1可知，系统处于大尺度周期态和混沌态时，Poincare 映射的非平稳性及振荡程度不同。大尺度周期态的Poincare 映射表现为不动点或在噪声影响下以不动点为中心的小邻域内小幅度振荡特征，而混沌态的Poincare映射表现为随机大幅波动的布朗运动特征。

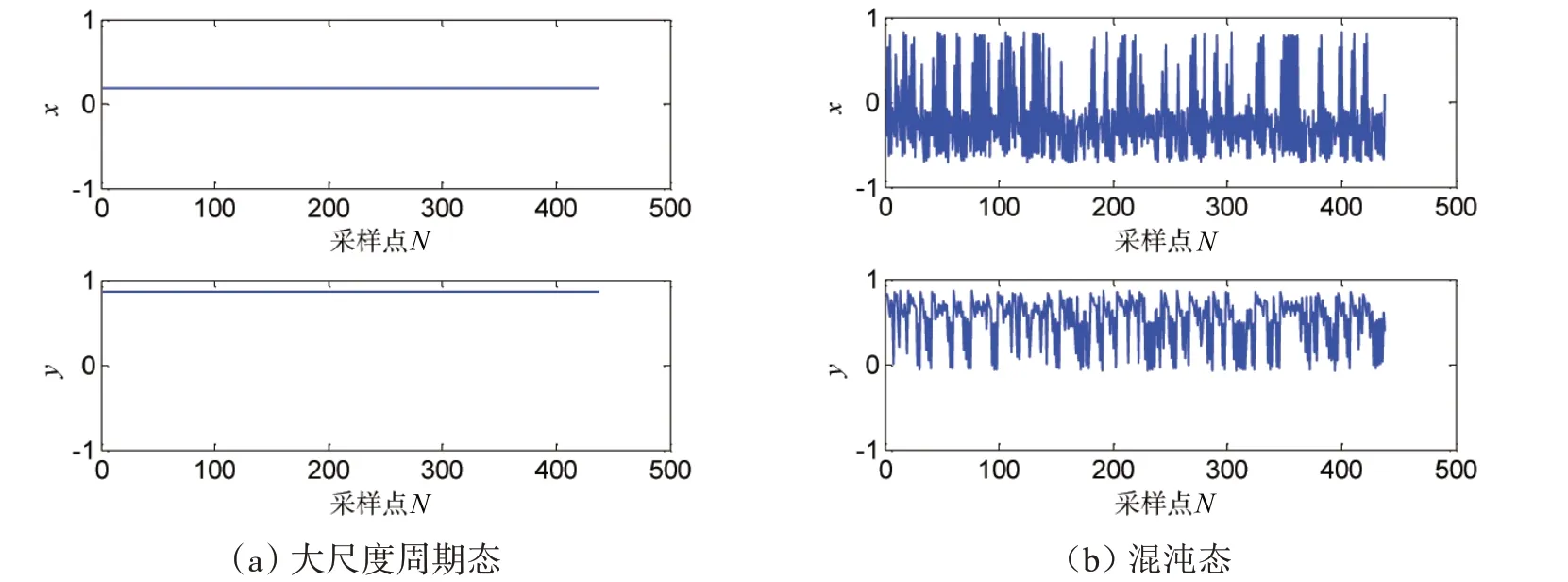
图1 φ = π/2时系统Poincare映射时序图Fig.1 Poincare section and mapping with φ = π/2

根据上述分析，构建一个可量化描述系统相态的度量参数Poincare 映射特征函数（Poincare mapping characteristic function，PMCF）：

式中，di为系统观测量的Poincare映射序列，N为序列长度，α为特征指数。

2.3 算法流程

基于上述分析，提出了基于FRFT 的变频Duffing 振子弱LFM 信号检测方法，检测流程如图2 所示。

具体检测步骤如下：

（1）根据发射信号先验信息，对接收信号进行最佳分数阶傅里叶变换。

（2）对变换后的FRFT 谱进行傅里叶逆变换（或再次进行旋转角度为α = -π/2 的分数阶傅里叶变换），并进行解调频。

（3）建立Duffing振子检测系统，系统参数阻尼比k = 0.5，给定系统混沌临界幅值rd值及频率扫描初值f = f0。

（4）将解调频后信号送入Duffing 振子检测系统，由单频信号频率估计范围设置步长Δf及扫描区间[ f0,fend]。运用龙格-库塔迭代法求解微分方程组，求取系统解的Poincare 特征函数值ηi，将其与给定的阈值ηd比较。若ηi＜ηd，说明接收信号中与策动力同频弱周期信号，即该段数据中包含弱LFM 回波信号；若ηi≥ηd，改变内置策动力频率fi+1= fi+ Δf。

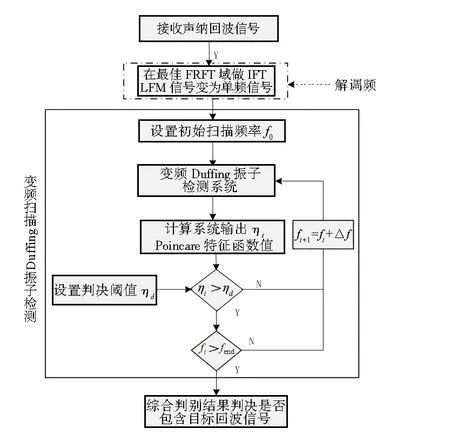
图2 基于FRFT变换的变频Duffing振子检测流程Fig.2 Detection process of variable frequency scanning Duffing oscillator based on fractional Fourier transform

（5）重复步骤（4）的过程，直至频率终值扫描结束，画出频率与系统Poincare映射特征函数关系曲线，根据扫描结果进行最终判决。

2.4 数值仿真分析

LFM 信号由数值仿真构造，幅值A= 0.08，归一化频率为f = 0.05～0.1。混响来自实测湖试数据，信混比SRR = -18 dB，数据长度N = 2 048。

采用匹配滤波方法检测结果，如图3 所示，由于信噪比较低，从图中无法检测出是否含有LFM 信号。采用本文提出方法的检测结果，如图4 所示。图4（a）和（b）为混响背景下LFM 信号的时域波形及频谱图，图4（c）和（d）为经分数阶傅里叶变换解调频信号时域波形及频谱图，从频谱图中可看到有一单频分量信号。利用变频扫描Duffing 振子法检测该单频信号，从图4（e）可以看出，在横轴频率为3.4 Hz处，系统的Poincare 映射函数值低于给定阈值，说明解调频信号中含有该频率的单频信号，且声散射回波数量为1。系统相图4（f）为Duffing 振子系统共振时的系统相图，也同时验证了被测信号中存在弱LFM目标回波信号。

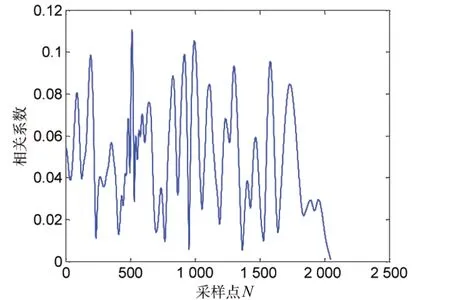
图3 匹配滤波Fig.3 Detection result of matched filter

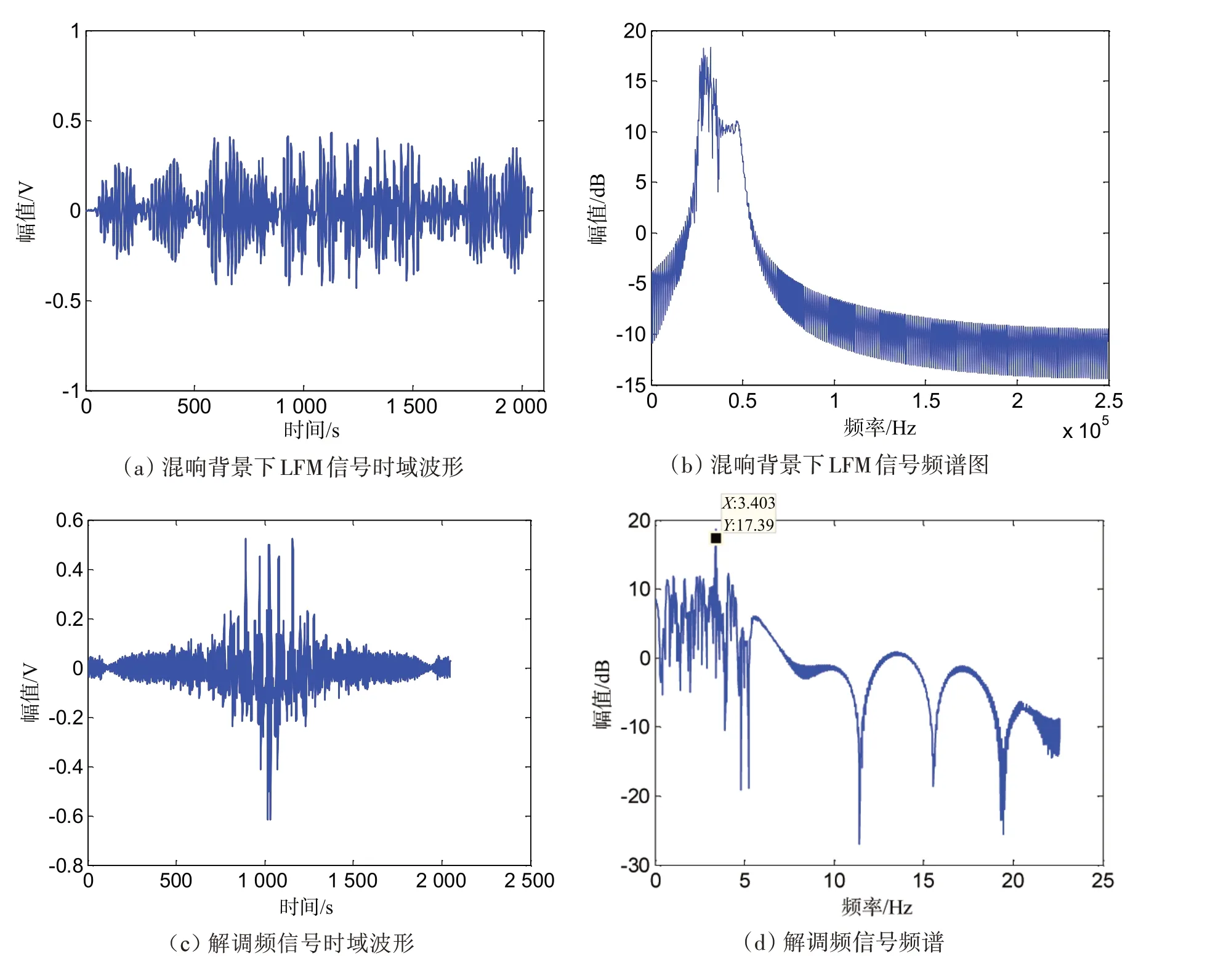
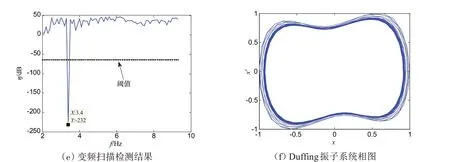
图4 混响背景下LFM信号检测结果Fig.4 Detection results of LFM signal under reverberation background

3 实验数据处理

3.1 湖试沉底目标检测

数据来自松花湖某区域沉底目标探测实验，湖底坡度大概为8.8°。沉底实验装置是由测量船、收发合置换能器、小舢板及水下目标构成。测量船系缆固定在岸边，船尾安装吊放支架用于起降收发换能器阵。水下试验目标用小舢板拖至远处自舷侧吊放水中，目标为球冠状圆柱壳体，壳内注入部分水。声呐发射频率、脉冲宽度和脉冲重复周期均为可调的LFM 信号，归一化频率为0.05～0.1，脉冲宽度Td= 2 ms。某基元接收到的信号如图5（a）所示，对该信号作匹配滤波处理结果见图5（b）。

图5 接收信号波形及匹配滤波Fig.5 Received signal waveform and matched filter

由于水下目标的布设离声呐接收阵列较远，接收到的初始时间序列主要为湖底混响，混响强度随时间逐渐减弱，环境噪声成为主要干扰。由于回波强度明显高于噪声强度，从图5（a）中可以明显看出有回波信号存在。为验证本文方法的有效性，截取目标回波数据，幅值减少五倍后将其左移至混响较强区域。处理后信号时域波形见图6（a）所示，匹配滤波结果见图6（b）所示，由于存在混响强干扰不能完全确定有目标回波存在。

采用本文方法对数据进行处理，首先在最佳分数阶傅里叶域进行解调频，解调后信号的时域波形见图7（a），频谱见图7（b）。由图7（b）可知，该频谱具有窄带特性，观察不到有单频线谱存在。其次，将解调频信号送入变频扫描的Duffing振子检测系统，并根据图7（b）确定频率扫描范围f∈[1.5 8]Hz。对每次变频扫描的Duffing 系统解求取PMCF 值。图7（c）为经变频Duffing 振子检测系统扫描后的结果图，横轴为扫描频率，纵轴为Duffing振子系统输出的Poincare特征函数值，低于给定PMCF阈值说明待测信号中含有弱周期信号。最后，结合该频率下的Duffing 振子系统相图7（d）进行综合判决，可判别出该测试样本中含有目标LFM回波信号，且声散射回波数量为1个。

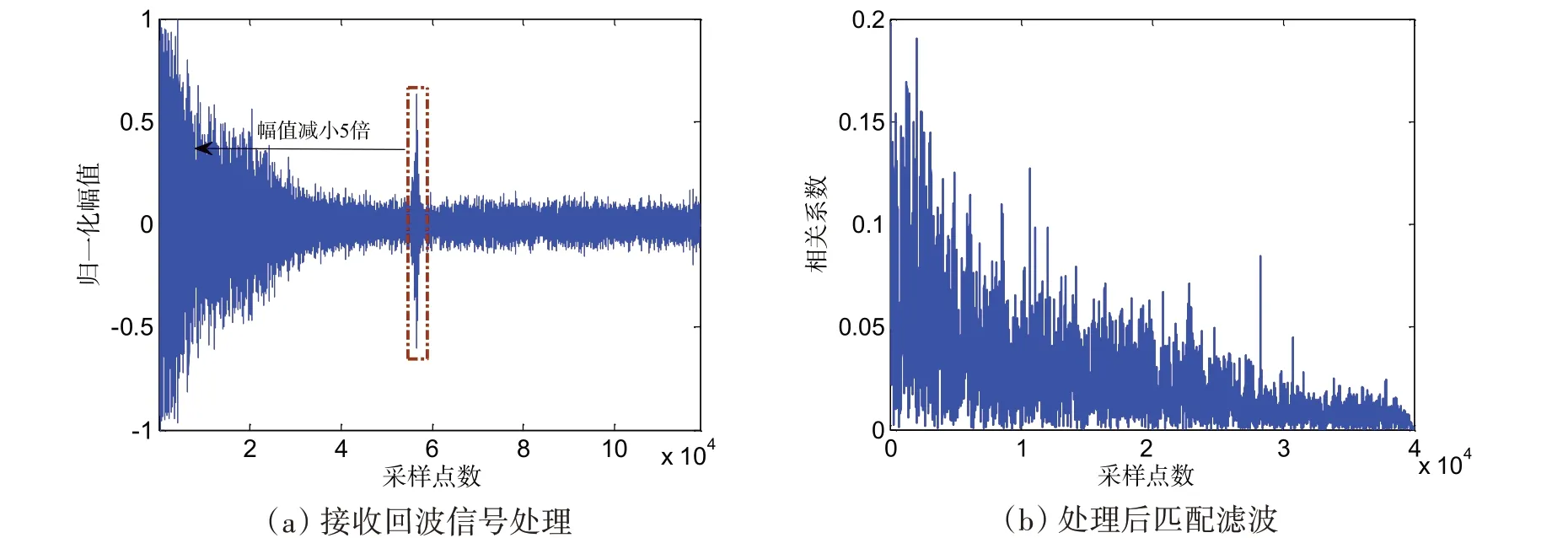
图6 接收信号处理后时域波形及匹配滤波Fig.6 Processing schematic diagram of the received signal

图7 本文方法检测结果Fig.7 Detection results using the method in this paper

3.2 海试掩埋目标检测

实验在地势平坦的泥沙海底中进行，掩埋目标通过悬浮目标牵引来标定埋放位置，配备收发合置声呐的测量船只通过“往返走航”的方式，在目标上方以不同掠射角发射LFM 信号对掩埋目标进行探测，见图8 所示。发射LFM 脉冲信号归一化频率值f0= 0.03～0.06，脉冲宽度T = 2 ms。图9 为掠射角90°时两次往返走航时接收回波信号能量随时间-距离的时域匹配图。从图9中可以清晰地观测到悬浮目标回波亮点（图中方框标出位置）及海底界面的深度；而对于掩埋目标，由于声波透射到沉积层，声能被吸收衰减严重，且受反射回波干扰，从时域匹配图中无法观察到掩埋目标的回波成分。

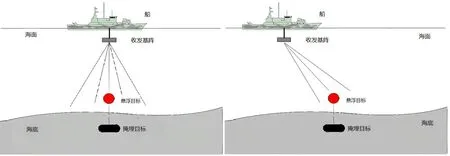
图8 海试掩埋试验示意图Fig.8 Schematic diagram of burying detection in sea trial

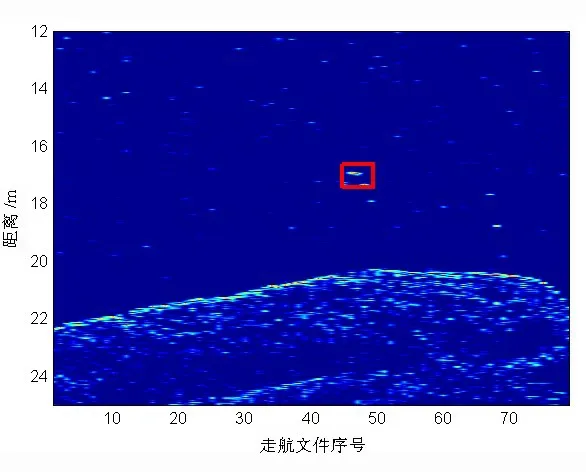
图9 掠射角90°走航文件时域匹配图Fig.9 Time domain match under different azimuth

图10（a）为回波信号的时域波形，图中虚线框1内的强回波信号为悬浮目标的几何散射回波。由于悬浮目标与接收阵的距离较海底及掩埋目标近，因此其回波信号到达接收装置的时间较短。虚线框2内的回波信号为强海底散射及掩埋的目标回波。将回波信号与发射信号作相关处理，图10（b）中的一较强相关峰值（图中圆圈标注）为悬浮目标回波与发射信号的相关峰；后续分析中由于较强海底混响干扰，从后面相关处理结果无法确定是否具有掩埋目标。

图10 掠射角90°回波信号Fig.10 Analysis of the received signal

为简化分析过程，略去悬浮目标回波信息，截取图10（a）虚线框2 中的回波信号。采用本文提出方法对回波数据进行处理，分析结果见图11所示。

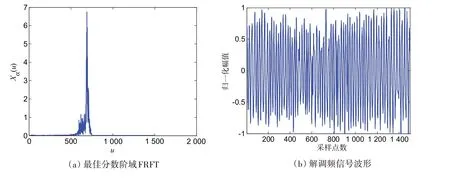
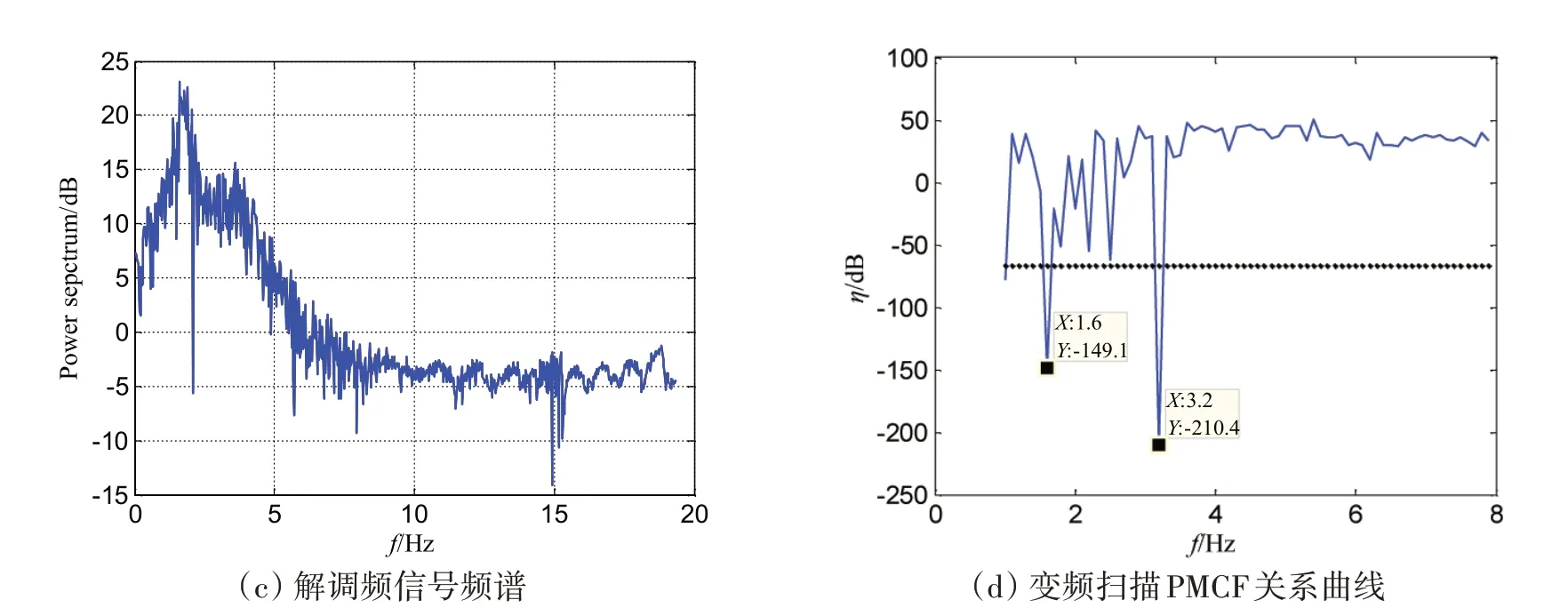
图11 本文方法检测结果Fig.11 Detection results using the method in this paper

根据发射信号先验信息，确定分数阶傅里叶变换的最佳阶数，对回波信号进行分数阶傅里叶变换，如图11（a）所示。在最佳分数阶域进行解调频处理，解调后信号的时域波形及频谱图如图11（b）～（c）所示。将解调频后的信号送入变频扫描Duffing 振子检测系统，系统检测的扫频结果见图11（d）。从图11（d）中可观察到有两个单频分量，可知掩埋目标的亮点声散射回波数量为2 个，声纳接收的回波信号中包含有掩埋目标回波信号。

4 结 语

本文针对低信混比下宽带信号—LFM 目标回波信号的检测问题，结合分数阶傅里叶变换理论，提出了基于分数阶傅里叶变换的变频Duffing振子检测方法。利用LFM 信号在最佳FRFT的时频能量聚集特性，LFM 信号的谱特征呈现δ 冲击函数特征，通过傅里叶逆变换进行解调频处理，使LMF 信号满足Duffing 振子系统检测前提条件。根据亮点模型理论，理论分析了目标回波存在多亮点声散射成分时解调频后的信号模型。研究发现，解调频后信号的频率受亮点时延、采样频率及数据时宽等因素影响而发生偏移现象。在上述研究的基础上，本文改进了常规Duffing 振子检测模型，提出变频Duffing振子检测方法，与PMCF相态定量判别方法相结合，仿真实现了信混比低达-18 dB下的LFM 目标回波信号检测。通过湖试及海试实测数据分析，也验证了本方法的可行性及有效性。