浮体带漂角拖航阻力预报

徐嘉雯，于雁云，林 焰

（大连理工大学船舶CAD工程中心，辽宁大连116024）

0 引 言

浮式结构物在受限水域航行或处于无自航能力状态时，以及建造完成后运输到指定安装地点的过程中，都必须依靠拖轮进行拖带作业。拖曳过程中，会受到各种风浪流的影响和航道的限制，为保证拖航安全，随时需要调整航向、注意避让，采取各种转弯以及旋转操作，被拖物体随着拖轮沿线航行，基本上时刻处于带漂角的拖航状态。

目前对于各类浮式结构物拖航阻力开展的研究有很多，主要有三种方式：经验公式估算[1-3]、模型试验和数值仿真。现在众多学者还是主要集中于研究纵向拖航，且一般侧重于考虑半潜式钻井平台[4-5]、防波堤[6]、多体船[7]等浮式结构物的各种结构形式或浮体浸没深度[8]对拖航阻力的影响，也有针对湍流模型选取对阻力预报精度影响的研究[9]，但带漂角拖航的研究暂时还比较少，且大多学者选择单一地通过数值模拟或者单纯的模型试验来分析流动特性和变化规律。比如，曾祥堃等[10]对不同迎流角下大型沉井的拖航工况进行了数值模拟。朱建国等[11]针对管节浮运进行了模型试验，探究其在不同流向角时的拖航阻力，基于此提出了编队方案。刘为民等[12]基于CFD 对典型拖航角度下平台的拖航阻力和流场分布特性进行了分析。Ommani等[13]研究了侧壁式平板在不同漂角时的受力情况，并将不同计算方法和试验值进行对比研究。田喜民等[14]模拟了KVLCC2 模型在小漂角斜航运动时的粘性流场，得到0°、3°、6°、12°漂角下的水动力特性，比较了SST k-ω和RNG k-ε湍流模型的模拟结果，并与试验值对比，认为SST k-ω 湍流模型更适合船舶斜航运动时的数值模拟。相比于纵向拖航，实际工程中带漂角拖航的情况更为普遍，且不仅仅局限于小漂角的情况，若能针对不同拖航方向提供更为精确的拖航阻力数值预报，对后续拖航作业中拖缆安排、编队布置等方面都将能够提供更为安全可靠的参考。

目前对于纵向拖航问题的数值预报研究已经比较成熟，但是带有漂角的拖航问题是更复杂的高雷诺数非对称分离流动，针对不同漂角时的数值模拟方法不尽相同。因此本文针对这类问题展开研究，以浮式闸门为研究对象，借助FLUENT软件对其不同漂角下的拖航性能进行数值分析。

1 基本理论

1.1 控制方程

考虑浮体处于一定的漂角状态，以一定速度被拖带的情况时，一般假定浮体静止不动，水流以一定速度从远处流过来。由于现在工程应用上DNS 方法和LES 方法受到计算机资源的限制，所以选取的合理解决办法是放弃流场中各种尺度的脉动信息，选择工程实际比较关注的湍流要素时均值，因此考虑以时均化的连续方程和时均化的动量方程为控制方程。

连续方程为

动量方程为

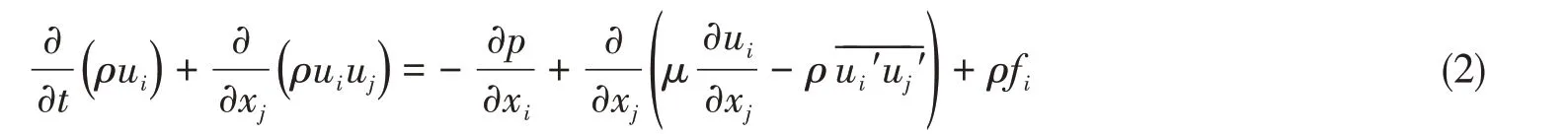
式中：t为时间；μ为流体的动力粘性系数；ui和uj为速度分量；ui′和uj′为速度分量脉动值；fi为质量力；p为流体的压力；ρ为流体的密度。

1.2 湍流模型

RANS 方程虽然经过时均化，但未知量的个数大于已有方程数，必须选择相应的物理模型使方程组封闭。本文采用涡粘模型中的RNG k-ε模型和SST k-ω模型。

RNG k-ε模型的基本未知量k和ε对应的输运方程为

式中：Gk表示平均速度梯度造成的湍动能生成项；Gb是由浮力引起的湍动能生成项；YM代表可压缩湍流中的波动扩张造成的整体耗散率；C1ε，C2ε，C3ε是常量；αk与αε分别表示k 和ε 的有效Prandtl 数的倒数；Sk和Sε是用户自定义源项。

与SST k-ω模型的基本未知量k和ω对应的输运方程为

式中，Gk表示湍动能生成项，Gω为耗散率生成项；Γk和Γω分别代表k 和ω 的有效扩散项；Yk和Yω则分别代表k和ω的耗散项；Dω代表交叉扩散项；Sk和Sω是用户自定义的源项。

1.3 自由液面模拟

涉及到气液两相流时，需要模拟水面和空气的交界面，本文选用VOF 方法模拟自由液面的运动，控制方程为

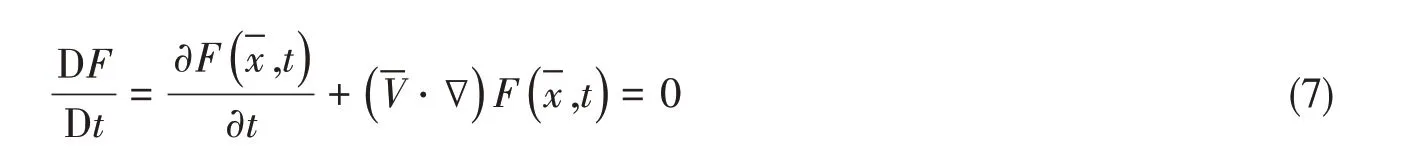
取空气为第一相，水为第二相，F = 0表示网格中都为空气；F = 1表示网格中都为水；0 ＜F ＜1表示含有流体界面的网格，称为界面网格，网格中既有空气又有水。

2 模型试验

本文以水电站的浮式闸门为研究对象，闸门的实际尺寸如表1所示，实际闸门和模型的缩尺比为15。模型试验在大连理工大学船舶拖曳水池中完成，该水池长170 m，宽为7 m，水深为4 m。运用EFD 法模拟闸门在静水中的拖航过程，通过改变拖曳速度和拖曳角度来进行模型试验，以验证数值方法的正确性。

本次闸门拖航性能试验是将一定比例制作的模型安装于模型架上，用模型架上的X、Y 两个方向的拉力传感器来采集合成闸门模型在静水中拖航时受到的水阻力，模型架如图1（a）所示。试验前先精确对位流向角，然后按照试验速度启动拖车，待拖航速度稳定一段时间后，数据采集过程即完成，随后对拖车进行制动停止。之后再将拖车退回到初始位置，准备进行下一次试验。针对每种拖航工况都进行两次重复试验，以此来保证试验数据的可靠性和正确性。试验过程图如图1（b）所示。

表1 闸门尺寸Tab.1 Size of gate

图1 模型试验Fig.1 Model test

3 数值计算模型

为避免相似率换算带来的误差，本文数值计算模型为与模型试验对应的模型，水的密度、粘性等参数直接取试验对应的参数。针对漂角为30°、45°、60°、90°的情况分别进行建模。因四种计算模型的建立方法类似，只是闸门在流场中的方位角度不同，因此仅以45°来流方向为例，给出计算模型和控制域，如图2 所示。考虑计算域时，闸门距水流入口为1 倍的跨距（跨距即闸门的宽），距水流出口为4倍的跨距，距计算域顶部为1倍跨距，距计算域底部为1.5倍跨距。为了忽略侧壁边界对水流的影响，设置闸门到计算域侧壁的距离均为1个跨距。

图2 计算模型和控制域Fig.2 Computation model and control domain

进行边界设置时，进流面设置为来流速度入口边界（velocity inlet）；出流面设置为压力出口边界（pressure outlet）；设置流域两个侧壁面和流域上表面为对称面边界（symmetry）；流域底面可设置为无滑移壁面边界（wall）；闸门的表面设置为无滑移壁面边界（wall）。边界条件设置如图3所示。

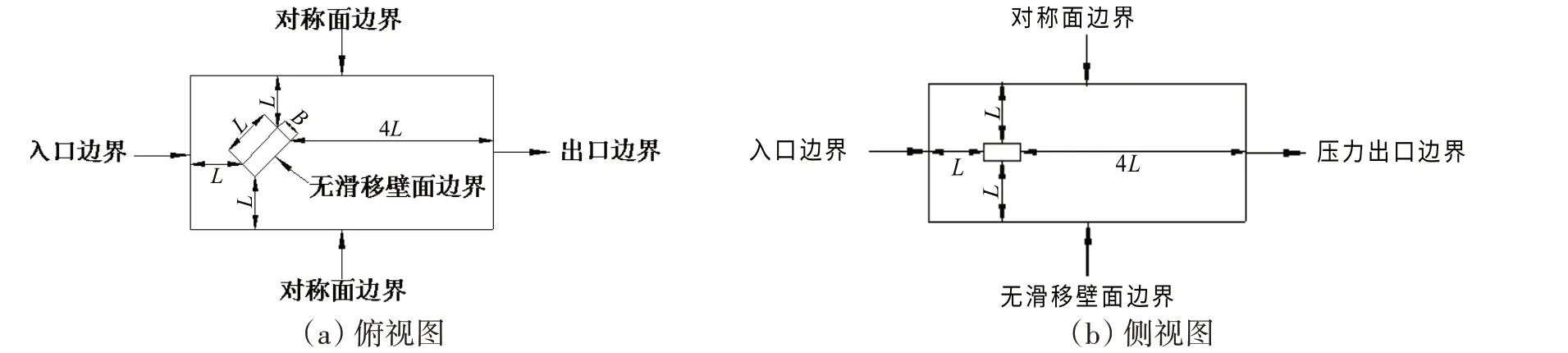
图3 边界条件Fig.3 Boundary conditions

网格划分需遵循保证网格质量和控制网格数量的原则，以漂角45°为例，模型的网格划分和网格细化情况如图4所示。为了得到针对不同漂角下的拖航阻力数值预报的较优方法，本文对每一漂角分别采用不同的网格划分方案，探究其对预报结果的影响。

图4 网格划分Fig.4 Mesh generation

4 数值结果分析

4.1 网格划分方案选取

对于不同漂角的拖航工况分别得到三套网格划分方案，加密程度依次增强，方案1对应的是粗糙网格，方案2对应的是精细网格，方案3对应的是细化网格，不同漂角下的网格方案汇总如表2所示。

每个漂角选取三组典型的网格划分方案，每种方案均在上一种方案的基础上进行一定程度的加密，数值计算时选择的所有参数均一致，比较同一漂角下不同网格划分方案的计算值。由图5 可见，网格数量越多，计算结果越趋于稳定。网格数太少，会造成计算结果偏高，计算可信度不足；网格数量太多，计算可靠性越好，但计算成本也越高。以45°漂角为例，给出网格1 和网格2 以及网格3 时的波高云图以及试验拍摄的波高图，如图6所示，网格3对于流场的捕捉最为精确，尤其是尾部大面积的流场细节。网格2得到的数值结果比网格1的数值结果更能精确描述闸门周围的波浪细节，尤其是闸门的来流面。因此综合计算精度和计算时间考虑，对于30°、45°、60°、90°漂角，均选取2 号网格划分方案。

图5 不同的网格方案计算结果Fig.5 Computational results of drag resistance adopting different grid partitioning schemes

表2 不同漂角下的网格划分方案Tab.2 Computational grid schemes of gate against drift angles

图6 45°漂角时不同网格方案的波高图与试验图的对比Fig.6 Comparison of wave height contours with different grid partitioning schemes and test results at 45°drift angle

4.2 湍流模型选取

影响数值模拟结果的因素有很多，其中湍流模型的选择至关重要。本文主要考虑k-ε 湍流模型和k-ω湍流模型这两个系列。借鉴前人的经验，选取RNG k-ε湍流模型以及SST k-ω湍流模型进行研究，得到的相应数值模拟值与EFD法得到的结果对比如图7所示。

图7 不同漂角下的拖航阻力Fig.7 Drag resistance against drift angle

对比不同漂角下的阻力预报值和模型试验值，阻力的增长随着速度的增加成非线性关系，航速对于阻力的影响非常大。结合表3的结果，漂角为45°时的预报误差最大；漂角小于45°时，采用SST k-ω湍流模型模拟吻合度较好；漂角大于45°时，SST k-ω湍流模型和RNG k-ε 湍流模型吻合度都比较理想。对比两种湍流模型，采用SST k-ω 湍流模型模拟误差都在10%以内，模拟精度一直比较稳定；RNG k-ε 湍流模型在大于45°漂角的工况时，精度有很大的提升；但是当漂角小于45°时，误差均超过10%，预报的精度不够稳定。

总体来说，RNG k-ε 湍流模型适用于充分发展的湍流流动，对于30°和45°漂角的情况，流动还是比较贴近于壁面，近壁面区域流体流动受粘性影响还比较大，如图8（a）和图8（b）所示，此时该模型的预报精度不是很理想，但当漂角为60°和90°时，如图8（c）和图8（d）所示，水流形成大面积的漩涡，几乎没有紧贴壁面的流动，湍流发展比较充分，此时该模型的模拟精度非常高。而SST k-ω 湍流模型稳定性很好，适合模拟近壁面不充分发展的流动，很适合处理旋转流问题以及模拟边界层处大范围的分离流动，对于各个漂角下的模拟精度均能满足工程实践的要求。

对比不同漂角下自由表面的速度矢量图，可以发现物体背流面流动随漂角变化很大。迎流面的水流接触物体后紧贴物体表面，顺着物体轮廓向后流动，流动比较顺滑；而背流面的水流流动与物体分离，在物体后方形成漩涡。漂角越大，背流面的漩涡生成中心在垂直方向距离物体越远；漩涡范围也随着漂角的增大而逐步扩大。迎流面和背流面的水流在物体前端点分离后，于物体末端附近汇合，从图8 中可以看到30°和45°漂角时，迎流面和背流面的两股水流汇合后融为一体向下游流动；而60°漂角时迎流面和背流面水流汇合后在物体末端附近又形成了一个漩涡，然后一起向下游流动；90°漂角的情况比较极端，在物体背流面两端形成两个完全对称的漩涡，其实可以看成60°漂角时流动情况的一个延伸。

表3 数值模拟误差Tab.3 Error of numerical simulation results

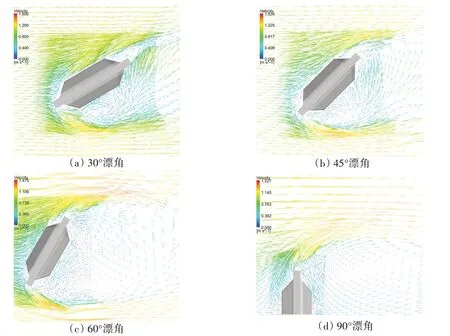
图8 速度矢量图Fig.8 Velocity vector diagram

除了自由表面展现的流动特征，水下的水流流动更具有复杂多变的特点，且各个漂角存在很大差异。为了更好地观察闸门水下部分周围水流的流动和漩涡生成情况，从闸门底部的视角研究水下水流流动，以下的数值分析均基于该视角。

30°漂角下整个流域的流动情况如图9所示，闸门周围的流场可以观察到漩涡的产生，尾流场可以明显看到大范围的水流螺旋流动。通过建立如图9（a）所示的平面分割流场，分别是Z系列平面，即沿Z 方向建立高度为-0.55 m、-0.45 m、-0.35 m 的平面及自由液面；X 系列平面，即沿X 方向建立x 值为2 m 的平面。观察各截面信息，了解水面以下的流动情况，捕捉详细的流动细节。相应的分辨率下捕捉到三个表面流动分离点，这三处分离点基本处于同一高度，如图9（b）所示。1、2处的分离点生成漩涡A，3 处的分离点生成漩涡B，如图9（c）所示。漩涡A 向闸门底部发展，z 为-0.45 m 的水平面上的流动情况能够捕捉到该漩涡的细节，直到z 为-0.55 m 时消散，汇入尾流的大螺旋流动中；漩涡B 向水面方向扩散和运动，z为-0.35 m的平面和自由面上的流动细节，均能清晰地观察到其流动轨迹。

图9 30°漂角下的流动情况Fig.9 Flow field at 30°drift angle

45°漂角下整个流域的流动情况如图10 所示，闸门背流面的漩涡范围广且流动复杂，尾流场同样可以看到大范围的螺旋流动。为了更精确描述水下的螺旋流动，选取一些平面切割流场，分别截取z系列平面，即z为-0.7 m、-0.6 m、-0.55 m、-0.5 m、-0.45 m和-0.35 m的平面捕捉漩涡结构；x系列平面，即x=2 m 的平面观察尾涡的流动情况；XY 系列平面，即垂直于闸门并距离闸门中心-0.4 m、-0.2 m、0 m、0.2m、1m 的平面观察漩涡流动情况；同时为了更好地观察漩涡B 的结构，在相应的位置进行截面，即XYZ 平面，观察其漩涡形态，如图10（a）所示。相应分辨率下观察到的闸门表面流动分离点1、2、3、4，如图10（b）所示。分离点在闸门背流面生成漩涡A、B、C，如图10（c）所示。分离点1、2、3 处生成并发展成为漩涡A，向下游发展成为尾迹漩涡的一部分。分离点4 处得到流线加入漩涡B 后，发展运动至漩涡C，且自由表面的流动生成漩涡C，向水深方向发展形成水下漩涡B。漩涡A 是沿水流方向发展，漩涡B是带一定倾角沿水深方向发展，漩涡C是直接沿水深方向发展。

图10 45°漂角下的流动情况Fig.10 Flow field at 45°drift angle

60°漂角下整个流域的流动情况如图11所示，背流面流动紊乱复杂，多股水流最终汇聚成一股，带有很大的螺旋性向下游流动，尾流依旧可以观察到大范围的螺旋流动。建立平面观察流场流动情况，如图11（a），XY 系列平面平行于闸门方向，距离闸门中心0 m、0.16 m、0.8 m 建立平面；Z 系列平面即沿z 方向-0.7 m、-0.45 m、-0.35 m 的平面及自由液面；X 系列平面即沿x 方向2.5 m 平面。在相应的分辨率下捕捉到闸门表面流动的四个分离点，如图10（b）所示。闸门表面底部1 和2 处位置区域脱离的流线成为漩涡A 的组成部分，该漩涡在A（a）位置处发展壮大，在运动过程中有部分流线按曲线轨迹运动到A（b）位置处再次形成漩涡并向下游运动；3 和4 处位置区域脱离的流线生成漩涡B，该漩涡在靠近自由液面时才逐渐成型，越靠近水面范围越大，如图10（c）所示。

图11 60°漂角下的流动情况Fig.11 Flow field at 60°drift angle

90°漂角下水下闸门周围的流动情况如图12所示，背流面漩涡范围广，与30°、45°、60°漂角时的尾流流动状态不同，未观察到螺旋流动。建立X系列、Y系列、Z系列平面观察流场流动情况，如图12（a）所示，X系列平面平行于闸门横剖面方向，即x坐标为0 m、0.2 m、0.45 m、0.6 m的平面；Y系列平面平行于闸门纵剖面方向，即y 坐标为2.5 m 的平面；Z 系列平面沿水深方向，即z 坐标为0.7 m、-0.65 m、-0.6 m、-0.55 m 平面。在相应的分辨率下未捕捉到闸门表面的分离点。a和b分别是漩涡A 在流动过程中的不同位置的漩涡中心，如图12（b）所示，漩涡A在a处形成和发展，范围很广，并逐渐向b处移动和加强。

图12 90°漂角下的流动情况Fig.12 Flow field at 90°drift angle

基于数值模拟结果分析闸门在处于不同漂角下水面和水下的复杂流场信息,观测到背流面的漩涡生成和发展情况，随漂角的变化各不相同，往往是由闸门背流面表面流动分离点上分离的流线生成或者闸门水下迎流面的流线流过闸门底部在背流面形成，漩涡扰动范围随漂角的增大而增大。

5 结 论

本文针对闸门处于不同漂角下的拖航性能进行了研究。在不同速度和不同漂角的各种组合工况下，采用不同的网格方案和不同的湍流模型进行数值模拟，并与试验结果进行对比分析，得出以下结论：

（1）对于浮体带有漂角的拖航问题，采用CFD 数值计算模拟，结合合适的网格划分方式、恰当的湍流封闭模型以及参数设置，可以达到较高的精度，算例中数值计算最优解与模型试验值的误差小于10%，满足一般工程问题对计算结果精度的要求。

（2）数值模拟时的网格划分方案需要兼顾计算时间和计算精度，本文在漂角为30°、45°、60°时采用网格数为70万左右的划分方案，漂角为90°时采用网格数为50万左右的划分方案。

（3）采用不同湍流模型模拟时，漂角为45°时的预报误差均最大；漂角小于45°时，流动发展还未充分，采用SST k-ω 湍流模型模拟吻合度较好；漂角大于45°时，湍流发展比较充分，SST k-ω 湍流模型和RNG k-ε湍流模型吻合度都比较理想，RNG k-ε湍流模型精度略高。与RNG k-ε湍流模型相比，对于不同漂角下的流场模拟，SST k-ω湍流模型稳定性更好。

（4）自由液面和水下的流动情况与漂角的大小密切相关，当漂角不大于45°时，自由液面上只观察到一个漩涡，漂角越大，漩涡越外扩，范围越大；当漂角大于45°时，自由液面能观察到两个漩涡，且漩涡范围也随漂角的增大而扩大，直至漂角为90°时，两个漩涡发展成为沿水流方向对称的两个完全一样的漩涡。通过对水下复杂流场的分析,发现背流面漩涡生成和发展情况随漂角的变化各不相同，往往是由闸门背流面表面流动分离点上分离的流线生成或者闸门水下迎流面的流线流过闸门底部在背流面形成，漩涡扰动范围随漂角的增大而增大。