波浪推进艇的集成电机推进器设计及航速预报

郑跃洲，王冬姣，叶家玮

（1.华南理工大学土木与交通学院，广州510640；2.中集海洋工程有限公司，广东深圳518000）

0 引 言

波浪推进无人艇应用了无人智能技术，在海上依靠波浪能推进可实现远距离的低速航行，替代有人艇进行海洋环境观测。无人艇在靠离码头，或航行中遇到障碍物需要紧急避碰时，需开启辅助动力系统。集成电机推进器IMP(Integrated Motor Propeller)是集电机、螺旋桨和导管于一身的新型电力推进装置，其吊舱式设计可实现自由转动，同时具有结构紧凑、安装布置方便、可靠性高、易维护、噪音和振动小的优点[1]，是无人水面艇和AUV的理想推进器。

集成电机推进器的设计涉及多个学科，包括电机设计和桨叶、导管的设计等。挪威科技大学Krøvel 等人[2]研制了表贴式永磁体、吊舱式安装的100 kW 船用集成电机推进器，通过实验证明了其比传统导管螺旋桨具有更好的水动力性能；武汉理工大学兰加芬等[3]分析了无桨轴型集成电机推进器的桨叶在不同叶切面处厚度分布对推进器水动力性能和桨叶强度的影响。在船舶自航的数值模拟研究方面，郑洋[4]考虑船-桨干扰问题，使用势流涡格法计算了螺旋桨的性能，应用迭代型体积力法对集装箱船模的自航性能进行了数值模拟，通过调节螺旋桨转速使船模达到预计航速；吴浩[5]等通过描述型体积力法替代螺旋桨力模拟了某双尾鳍型船模的自航，探究了虚拟盘的流入半径、厚度和偏移量等对自航航速的影响。

1 电机设计和空载分析

有桨轴型集成电机推进器由永磁无刷直流电机、导管、螺旋桨和撑杆等部件组成。现有波浪推进无人艇实艇的设计吃水为0.4 m，为了使推进器位于基线以上水线以下并考虑导管的尺寸，预估螺旋桨的直径为300 mm。鉴于KA 螺旋桨的叶梢呈圆弧状，易于与电机转子内表面的连接，将其作为使用桨。四叶的桨叶数有利于通过CNC 整体加工得到螺旋桨和转子，无需焊接。无人艇的目标航速为5 kn,通过螺旋桨图谱法预取电机的转速为1 000 r/min。由于无人艇携带的锂电池为48 V，电机的功率预取4 kW。电机尺寸不大，因此采用星形绕组接法，两相导通，三相六状态的导通方式，双层绕组，56 极、63 槽的分数槽和集中整距绕组方式，以及表贴式永磁体设计。通过Ansys RMxprt 模块，使用参数化设计法确定电机定子和转子的具体尺寸，得到电机的性能。电机主要性能为：效率89.14%，额定转速994 r/min，额定转矩38.4 N·m。电机安装在导管的平行中段处，参照JD-7704 导管浆，依据转子和定子的径向和轴向尺寸，修改了导管的形状，使导管内能够容纳电机。

螺旋桨和导管共同决定集成电机推进器的水动力性能，其中螺旋桨的旋转产生集成电机推进器的推力，导管的内表面形状影响推力的分布和产生的流阻。推进器工作时，电机的转矩需要大于螺旋桨和转子的转矩之和，转子的转矩可以由公式估算，依据导管桨的图谱，选择螺距比P/D=1.0 的KA4-55螺旋桨作为使用桨。图1为定子线圈实物图，图2为安装了螺旋桨、轴、电机转子铁心和N35永磁体的实物图，图3 为IMP 装配图，其中定子和转子铁心是由DW310-35 材质的硅钢片通过线切割和激光焊接得到。

图1 定子线圈实物图Fig.1 Stator coil

图2 转子和螺旋桨实物图Fig.2 Rotor and propeller

图3 IMP装配图Fig.3 IMP assembly drawing

2 桨叶结构强度分析

为了无人艇航行安全，必须保证辅助动力装置中的螺旋桨具有足够的强度，为此在设计集成电机推进器时须进行强度校核计算。流固耦合分析是流体力学分析和固体力学分析交叉耦合而生成的一门力学分析方法，它可分为两种：单向流固耦合分析和双向流固耦合分析。单向流固耦合分析是指耦合交界面处的数据传递是单向的，将CFD计算得到的结果传递给固体结构进行分析，但是没有固体结构分析结果传递给流体分析的过程。双向流固耦合分析的数据交换是双向的，既有流体分析结果传递给固体结构分析，又有固体结构分析的结果反向传递给流体分析。

2.1 计算方法验证

为验证计算方法的有效性，通过Star ccm+软件中双向流固耦合的瞬态计算方法，计算与本文设计的集成电机推进器具有相同螺旋桨的导管桨桨叶的结构强度，其桨叶材质为耐海水腐蚀的5083铝合金。设置的计算域包括螺旋桨和转子的固体区域、旋转域和静态流体计算域。在旋转域与固体区域之间创建流体-结构界面，在旋转域与静态计算域之间创建流体-流体界面。对旋转设备中的流动问题可以通过创建一个与旋转设备一起运动的坐标系来建模，即使用移动参考系法来处理，将转动参考系设在与螺旋桨一起旋转的流体区域（旋转域）上，螺旋桨的转速设置为994 r/min。计算时先冻结流体结构耦合求解器和固体应力求解器，待导管桨表面压力趋于稳定时，再解冻上述两个求解器进行双向流固耦合计算，最终得到导管桨在不同进速J 对应的水动力性能和桨叶结构强度，结果如图4 和图5所示。由图4可知：导管桨的敞水性征曲线与图谱试验值[6]接近，其中在系柱（J=0）状态下，导管桨水动力的平均误差为0.376%；当进速系数J小于0.6时，平均误差不到3%（平均误差为推力系数、转矩系数和效率误差的平均值）。由图5 可知：导管桨的桨叶最大应变和应力值均随着进速系数J 的增大而减小，符合实际情况，说明本文采用的双向流固耦合的计算方法合理可行。本文对桨叶强度校核均在系柱状态下进行。

图4 导管桨敞水性征曲线Fig.4 Open water characteristic curve of ducted propeller

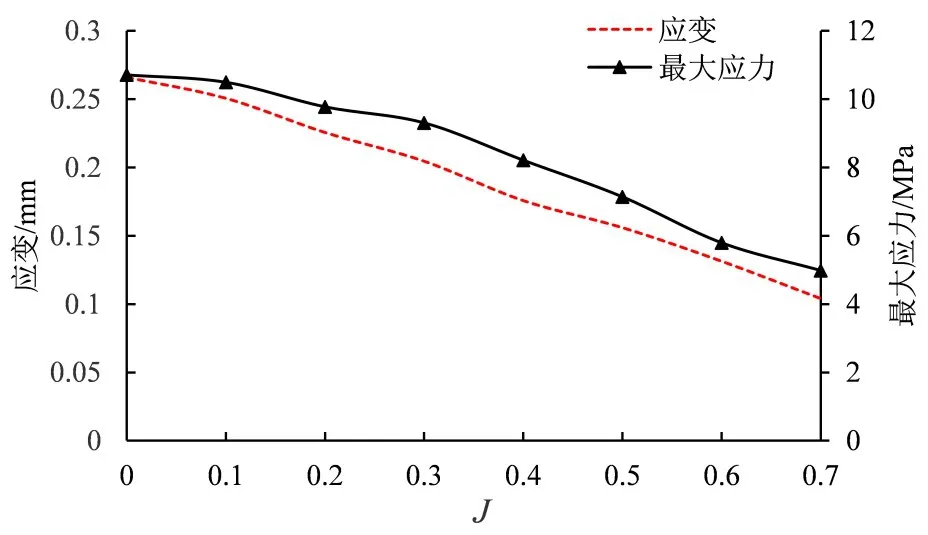
图5 桨叶最大应变和应力随进速系数变化曲线Fig.5 Maximum strain and stress of blades as function ofadvance coefficient

2.2 IMP桨叶强度分析

采用与2.1节相同的方法对有桨轴型集成电机推进器在系柱状态时进行桨叶强度计算，其中IMP的面网格、固体区域网格和网格剖面图如图6 所示，其中固体区域的网格数为50.8 万，旋转区域网格数为213.7万，静态计算域网格数为87.1万。

设置的转速为电机额定转速，计算得到在系柱状态时IMP的推力约为1 113.4 N，而使用相同螺旋桨的导管桨对应的推力为1 170 N。相同进速系数和转速时，IMP 的推力小于导管桨推力的主要原因是由于IMP的螺旋桨与电机转子连接，转子在导管内的旋转产生了额外的流阻，同时螺旋桨的轴向诱导速度降低。由图7 可知：有桨轴型集成电机推进器桨叶的导边和随边与轮缘内表面连接处有应力集中，最大应力为42.38 MPa，最大应变出现在转子处，最大值为0.231 mm，是桨叶直径的0.077%。5083铝合金的抗拉应力为270 MPa，依据公式（1），得到系柱状态下桨叶的安全系数约为6.36。

式中，kb为安全系数，σb为强度极限应力，[ σ ]为许用应力。

图6 IMP相关网格Fig.6 IMP related grids

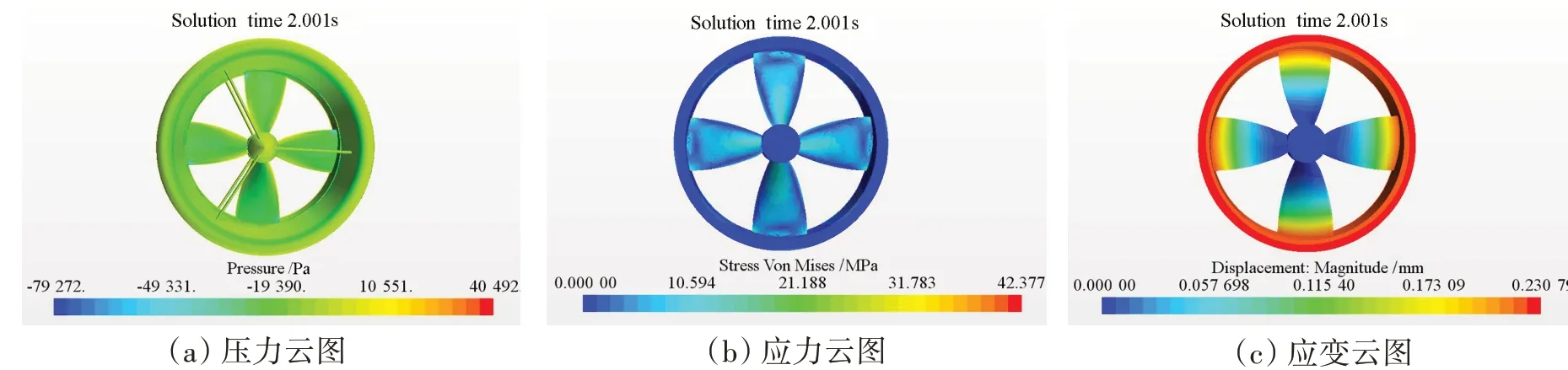
图7 系柱状态下IMP的压力、应力和应变云图Fig.7 Contours of IMP pressure,stress and strain in mooring state

在计算螺旋桨的强度时通常都是以船在全速航行时螺旋桨发出的推力及吸收的转矩为依据，考虑到船舶开航时，进速系数J 极小，从图5 可知，此时对应的螺旋桨应力大于全速航行时的数值。另外，常规螺旋桨在工作中可能会遭遇漂浮物的碰击而遭受突然负荷，因此常规螺旋桨所取用的安全系数较大（10 左右）。近年来国内外许多学者认为将安全系数降至8 左右为宜，对于内河船可取6 左右[7]。考虑到本文所研究的集成电机推进器，其导管可保护螺旋桨不与异物相碰，且以系柱状态进行计算，取安全系数6 作为螺旋桨强度校核判别标准，因此可认为本文设计的IMP 桨叶强度能够满足螺旋桨安全系数要求。

3 波浪推进无人艇航速预报

3.1 方法验证

本文研究的波浪推进无人艇是一艘双体船，在风浪中关闭辅助动力系统仅依靠安装在船首尾位于水面以下的水翼随艇体作纵摇和垂荡运动产生的推力实现无人艇向前低速行驶[8]。在静水中航行或遇到障碍物时才需要开启辅助动力装置。在无人艇进/出港遇到波浪较小的情况启用辅助动力装置，此时可将水翼保持在水下航行，也可以将水翼抬离水面以减小静水阻力。通过Star ccm+重叠网格法计算水翼抬离水面工况下船模的静水阻力，并与船模拖曳试验结果进行比较，以验证计算方法的可行性。无人艇模型的缩尺比为3，船模水线长为2.146 m，船宽为1.01 m，片体宽度为0.286 m，吃水为0.133 m，型深为0.233 m。数值模拟计算的坐标原点位于船体对称面首部静水面处，沿船首方向为x轴，z轴垂直向上为正。图8所示为船模阻力计算域和船体表面及y=1.0 m剖面处的网格图。

图8 船模静水阻力数值模拟计算域及网格图Fig.8 Numerical simulation calculation domain and grid diagram of ship model

图9 为船模静水阻力及纵倾随航速变化曲线，从图9 可以看出：数值模拟计算结果与船模拖曳试验数据曲线基本一致，船体总阻力和纵倾角的绝对值大致随着航速的增加而增大（船体纵倾角负值表示尾倾）。与拖曳试验结果比较，船模速度范围在0.594～2.079 m/s 时，数值计算的阻力平均误差为4.51%，最大误差为10.28%。进一步分析可知：在1.188～1.485 m/s 和1.782～2.079 m/s 航速范围内阻力增加较快，此时尾倾随航速增加而增大；在航速为1.485～1.782 m/s时船体总阻力和船模尾纵倾角变化不大，说明船体的航态会影响总阻力的大小。

图9 船模静水阻力及纵倾随航速变化曲线Fig.9 Variation curve of ship model still water resistance and trim as a function of speed

3.2 航速预报方法

体积力法是对螺旋桨的推力和扭矩等效建模，在不实际求解螺旋桨几何的情况下创建螺旋桨的推力和扭矩模型。该方法将体积力均匀地分布在圆柱形的虚拟盘体上，通过对螺旋桨盘面区域的计算单元表面施加轴向力和切向力，来模拟螺旋桨产生的推力和扭矩对流场的作用[9]。体积力fb在径向上会发生变化，其分力的径向分布遵循Goldstein的最佳分布，由公式（2）～（5）给出[10]：

式中，fbx为轴向体积分力，fbθ为切向体积分力，r为径向坐标，RH为轮毂半径，RP为螺旋桨半径。常数Ax和Aθ计算公式如式（6）和（7）所示：

式中，T为推力，Q为扭矩，Δ为虚拟盘体厚度。

体积力法有描述型和迭代型。描述型只需要输入转速、推力系数、扭矩系数、轮毂半径、螺旋桨半径、虚拟盘厚度等参数，通过经验公式计算桨叶的载荷分布，本文采用式（2）～（7）所描述的经验公式确定体积力，适用于螺旋桨设计的初期；迭代型则通过计算实际螺旋桨的敞水性能来获得体积力分布[9]。本文采用的是描述型，首先采用移动参考系法计算IMP 的敞水性能，即不同进速系数对应的推力系数和扭矩系数，如表1 所示，再将敞水性征曲线输入到虚拟盘计算体积力。

3.3 实艇在静水中航行时的航速预测

第一代波浪推进无人艇可通过连接桥两端的升降装置来升降首尾水翼。水翼形状为梯形，左右各一个，水翼本身重力与静浮力平衡，两端的翼型分别是NCACA-0018和NACA-0024，静浮时水翼处于水平状态。本节只分析实艇首部安装固定水平翼和船后安装一个IMP时的无人艇在静水中自航时的航速。水翼保持在水面以下，波浪推进无人艇的面网格和在航速为4.4 kn 时对应的船体周围水面分布分别如图10和图11所示。

表1 集成电机推进器敞水性能Tab.1 Open water performance of IMP

图10 波浪推进无人艇的面网格Fig.10 Surface grid of waves propelling unmanned boat

图11 航速为4.4 kn时船体周围水面分布图Fig.11 Distribution of the water surface around the hull at 4.4 kn

通过计算x方向（船长方向）净力来获得平衡入口流速，式（8）为x方向净力Fx的计算公式。

式中，θ为船体纵倾值，T为虚拟盘的总推力，Rt为船体总阻力。

本文安装的首固定翼在静浮时处于水平状态，即水翼的安装角为0°。式（8）中对应的船体纵倾角、虚拟盘总推力及船体总阻力皆为瞬时值。IMP 转速为994 r/min，对于静水中航行工况，取计算稳定后的一段数据进行平均，得到图12 和图13 中各自数据的平均值。对于规则波中航行的船舶，其Fx值是随遭遇周期波动的，可取计算稳定后若干个遭遇周期内的瞬时Fx值求其平均。从图12 可以看出：无人艇在静水中航行时，水翼位于水下1 m 深度处，主要受粘性阻力作用，其阻力随航速增大的曲线斜率明显小于无人艇总阻力曲线，其中航速为4 kn 时水翼阻力约为102 N，占总阻力的26.7%。由图13可知，纵坐标值为0的水平线与x方向净力曲线的交点对应的横坐标即为航速，安装首水平固定翼和一个IMP时，无人艇在静水中航行时的航速可达4.27 kn。

图12 静水总阻力和水翼阻力随航速变化曲线Fig.12 Total still water resistance and hydrofoil resistance versus speed

图13 x方向净力随航速变化曲线Fig.13 Net force in x direction versus speed

3.4 实艇在迎浪规则波中航行时的运动响应及航速预测

在3.3 节基础上，使用五阶斯托克斯波，预报无人艇在迎浪规则波中航行时的航速。模拟五阶斯托克斯波的波长为15 m，水深为100 m，波高为0.4 m。坐标系x 轴从船尾指向船首方向，z 轴垂直向上，采用右手坐标系，坐标原点位于纵中剖面船首静水面处，x=-3.39 m 为无人艇重心所在位置的纵向坐标值。在x=-3.39 m，y=10 m 处设置波面位移监测点，目的是通过分析垂荡、纵摇运动和波面位移的时历曲线，得到运动垂荡和纵摇运动的频率响应函数及相位角。图14 为无人艇航速是4 kn时，与船舶重心纵向位置相同点的波面位移时历曲线。对x=-3.39 m，y=10 m处，t=80 s前八个周期的波进行统计，得到的平均波高为0.358 2 m，约为设置波高的89.55%，遭遇周期为2.17 s。

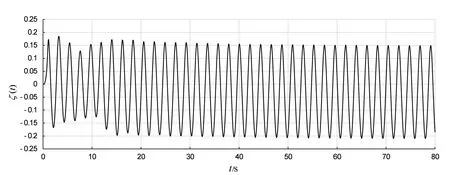
图14 航速4 kn时波面位移时历曲线（x=-3.39 m，y=10 m）Fig.14 Time history of wave elevation at 4 kn(x=-3.39 m,y=10 m)

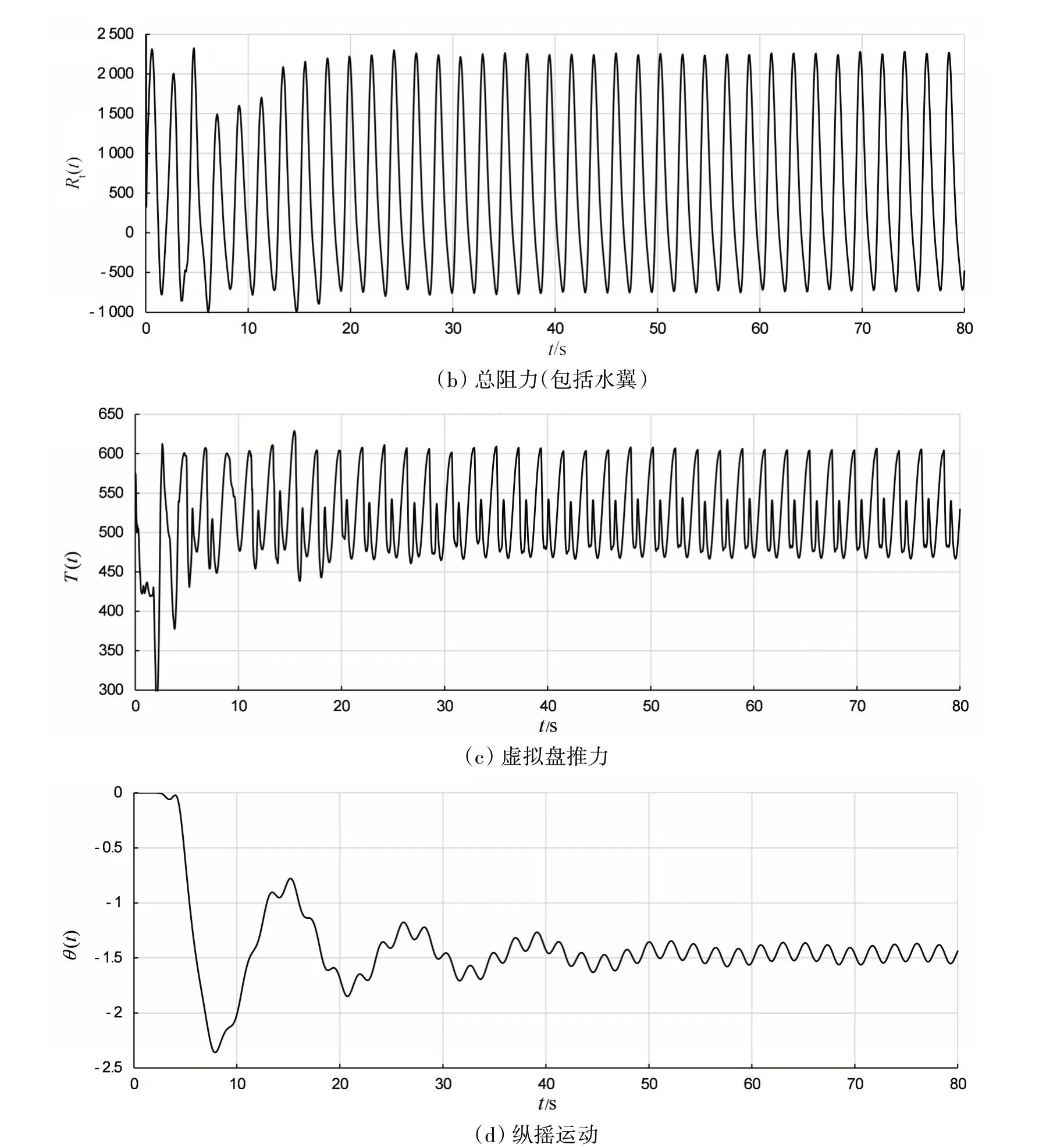
图15 无人艇在迎浪规则波中航行时的时历曲线Fig.15 Time-history curve of unmanned boat travelling in regular head waves

图15结果显示无人艇在迎浪规则波中，以4 kn的航速航行时的水翼受力、总阻力、虚拟盘推力的时历曲线和纵摇运动响应均呈周期性变化。在一个波浪周期内，作用在水翼上的水平力有2 个峰值和2 个谷值，即在一个波浪周期内出现了二次周期性循环，阻力和推力交替出现，两个峰值和谷值大小不等，水翼平均值为-13.2 N，负值表示推力；艇体、水翼及立柱在内的总阻力平均值是556.8 N，虚拟盘的平均推力为521.8 N，平均纵倾约为-1.46°，x方向的平均净力约为-35.2 N。因此基于首水平固定翼的波浪推进无人艇，在波长为15 m、波高约为0.36 m 的迎浪中航行时，航速预计略小于4 kn。船体纵摇双幅值为0.16°，可得纵摇频率响应函数为0.454°/m，纵摇与波面位移间的相位差为-152.6°。

图16 和图17 分别为波浪推进艇以4 kn 航速在迎浪规则波中航行时垂荡运动响应和t=80 s 时刻的波形图。可知垂荡运动双幅值为0.294 m，垂荡频率响应函数为0.82，与波面曲线对比可知，垂荡运动与波面位移之间的相位差约为21.6°。

图16 垂荡运动响应Fig.16 Heave motion response

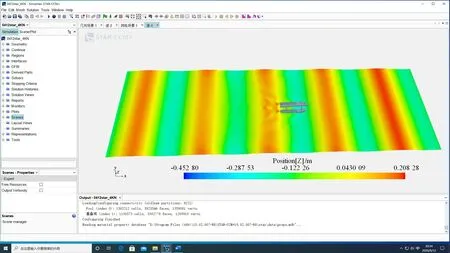
图17 以4 kn航速航行时的波形图（t=80 s）Fig.17 Free surface wave pattern at 4 kn(t=80 s)

4 结 论

本文通过等效磁路法设计了集成电机推进器所用的无刷直流电机，使用双向流固耦合方法校核了桨叶的结构强度，预测了含首固定水平翼之波浪推进无人艇在安装设计的集成电机推进器后分别在静水中和迎浪规则波中航行时的航速。研究结果表明：有桨轴型集成电机推进器的桨叶最大应力发生在叶梢与轮缘内表面的连接处，最大应变发生在转子外表面；描述型体积力法替代螺旋桨的作用能便捷且较为快速地预测航行器的航速，便于设计推进器的安装位置；波浪推进无人艇在静水中航行时水翼会产生较大阻力，而在波浪作用下，水翼随艇体摇荡，可产生推力。