基于IQGA-GRNN模型的SCR脱硝出口NO x质量浓度预测方法

曹喜果，张永涛*，李雅恬

（1.新疆工程学院能源工程学院，乌鲁木齐830091；2.河北华电石家庄鹿华热电有限公司，石家庄050000）

0 引言

NOx是危害人体健康、引起酸雨、诱发光化学烟雾、导致全球变暖的重要污染物［1］。燃煤电站是NOx排放大户，建立燃煤电站NOx排放数学模型是脱硝控制策略设计的前提，具有较强的理论和现实意义［2-3］。然而，选择性催化还原（SCR）烟气脱硝系统工艺复杂，建立其机理模型较为困难［4-6］。目前，一些先进的控制技术在SCR脱硝控制方面已得到应用，人工神经网络作为并行计算模型，对建模对象先验知识要求不多且有很好的非线性映射能力，因此，国内一些学者将神经网络引入SCR脱硝控制系统建模。翟永杰等［7］分析影响出口NOx质量浓度的因子，通过神经网络方式进行SCR脱硝建模。周鑫等［8］将核偏最小二乘算法（KPLS）和遗传算法（GA）结合，提出了利用GA-KPLS建模方法建立SCR模型。秦天牧等［9-10］采取多尺度核偏最小二乘法（MKPLS）建立SCR脱硝模型，并用预测控制方法实现了喷氨优化控制。

广义回归神经网络（GRNN）适用于解决非线性问题，在逼近能力及学习速度上具有较大的优势，样本数据较少时预测效果也较好［11-13］。GRNN结构简单，计算过程中只需确定一个参数——光滑因子σ，运算较为简单。σ的选择对GRNN的网络泛化能力和精度有重要影响［14］。

量子遗传算法（QGA）基于量子计算原理，将量子的态矢量引入遗传编码，利用量子逻辑门实现染色体演化，比常规遗传算法具有更好的局部搜索能力［15-16］。但传统QGA演化目标较为单一，量子旋转角取值不灵活［17-18］，对此，笔者采用动态调整量子门的方法对其进行改进，并利用改进量子遗传算法（IQGA）实现GRNN网络中光滑因子σ的寻优，从而建立IQGA-GRNN网络模型，提高SCR脱硝控制模型的精确度。

1 GRNN网络基本原理

GRNN网络结构如图1所示，它由输入层、模式层、求和层和输出层构成。网络输入X=［x1，x2，…，xn］，网络输出Y=［y1，y2，…，yk］。

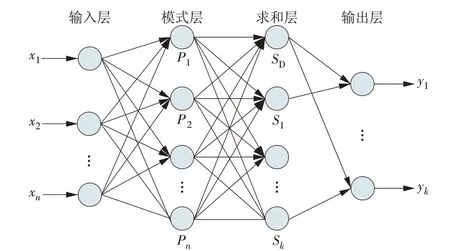
图1 GRNN网络结构Fig.1 GRNN structure

（1）输入层。该层神经元的数目与训练样本中向量维数相同，该层的作用是输入学习样本并将其参数传入模式层。

（2）模式层。该层神经元数目与训练样本数目n相等，第i个神经元的训练函数为

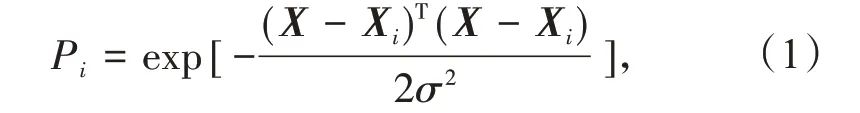
式中：X为网络输入；X i为第i个神经元训练样本，i=1，2，…，n。

（3）求和层。该层神经元为各神经元的加权和，模式层中第i个神经元与求和层中第j个神经元权值为输出样本中第j个元素值。传递函数为

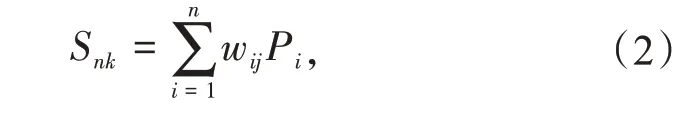
式中：wij为连接权重，为各训练样本的期望输出值；j=1，2，…，k。

（4）输出层。该层神经元数目与样本输出维数k相等，即求和层中2类神经元相除

式中：SD为求和层中各神经元的代数和。

2 IQGA原理

2.1 IQGA基本原理

量子遗传算法是量子计算与进化算法的结合，为了使该算法能更好地解决所研究问题，本文在此标准算法的基础上进行改进。在QGA中，量子旋转门的调整操作定义为

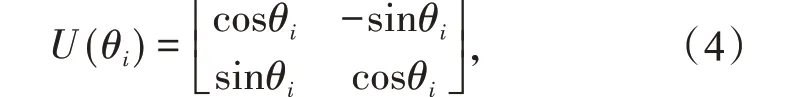
式中：θi为旋转角，取值范围为［0，π/2］。

染色体第i个量子的更新过程为

式中：［αi，βi］T，［α'i，β'i］T分别为染色体第i个量子通过旋转门前、后的概率幅值。

量子门更新原理如图2所示，图中：θ'为当前最佳基因值；θ为目前要更新的基因值。

图2 量子门更新原理Fig.2 Update of quantum gate

旋转门的目的是朝着有利于进化的方向更新种群，一般情况下量子旋转角度Δθ是固定的，但Δθ太小将导致算法收敛较慢，反之会出现算法早熟，从而给算法造成一定的限制，为此，采用动态旋转角可解决这一问题。动态旋转角策略可表示为

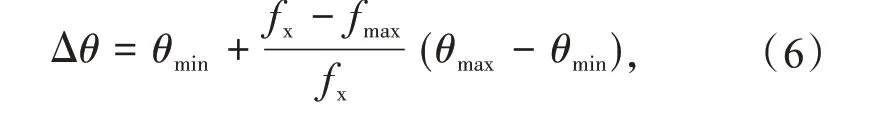
式中：fx，fmax分别为当前个体及最优个体的适应度；θmin，θmax分别为旋转角的最小值及最大值。

Δθ取值区间一般为［0.01π，0.05π］，fx与fmax的差值越小，旋转角越小，该策略既有利于染色体不断向最优解靠近，又有利于在最优解附近精细搜索。基于以上原理，IQGA算法流程如图3所示。

2.2 IQGA测试

为了验证IQGA的有效性，本文选取典型非线性函数进行GA，QGA和IQGA的对比试验。非线性函数在给定的范围内存在很多局部极值，常规的寻优算法容易陷入局部极值或在极值间振荡，式（7）中：-3.0≤x≤12.1，4.1≤y≤5.8。

图3 IQGA流程Fig.3 IQGA flow

maxf(x，y)=xsin2(4πx)+yxsin2(20πy)。（7）

试验中对3种算法分别测试100次，对最优值、最劣值和平均值进行对比。统计结果见表1，测试曲线如图4所示。

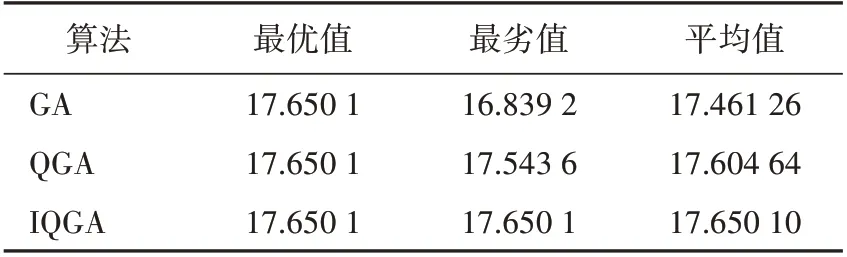
表1 3种算法测试结果对比Tab.1 Test results obtained by three algorithms

图4 3种算法的进化曲线对比Fig.4 Comparison of evolution curves of three algorithms

从表1可知，3种算法都能获取最优值，但IQGA的成功率达100%。从图4可以看出，进化代数不到20时IQGA已达到最优值，说明该算法拥有更好的收敛性，故本文采用IQGA算法进行参数优化。

3 SCR脱硝系统模型建立与仿真

3.1 建模背景

火力发电厂是NOx排放的主要来源之一，目前降低NOx排放主要有2种措施：一种是控制燃烧过程中NOx生成，即NOx优化燃烧［3］，但低NOx燃烧技术的脱硝效率仅有25%～40%，无法满足日益严格的环保标准；另一种是对生成的NOx进行处理，即烟气脱硝技术。本文针对第2种措施，根据脱硝系统机理，建立基于IQGA-GRNN的脱硝系统数学模型。

以某300 MW供热机组为研究对象，该机组脱硝系统采用SCR工艺，根据脱硝反应机理及数据库中实际测点情况，选择机组负荷、入口NOx质量浓度、入口氧量、入口烟气流量、入口烟气温度、喷氨量6个变量作为SCR脱硝系统模型的输入变量，SCR出口NOx质量浓度作为模型输出。图5为脱硝系统NOx排放影响因素取值范围及关系。

图5 脱硝系统NO x排放影响因素取值范围及关系Fig.5 Valuerangesof theinfluencing factorsof NO x emission from thedenitrification system and their influences

以30 s为采样周期，选取分散控制系统（DCS）的历史数据，剔除失真或不完整数据后，选择390组数据并将其分为2类。针对数据特点，取其中350组作为训练样本，其余作为测试样本。图6为部分现场实测数据变化情况。

图6 部分现场实测数据变化趋势Fig.6 Variation trends of some field data

3.2基于IQGA-GRNN的SCR脱硝系统建模

将选取的6个输入变量进行归一化处理后，分别代入IQGA-GRNN预测模型进行训练。利用IQGA算法优化GRNN模型的光滑因子，以目标函数值（σ的适应度）最小为原则，实现GRNN网络中光滑因子σ的寻优，σ的适应度为IQGA算法最大进化代数为100，种群大小为40，采用二进制编码，其最优个体适应度曲线如图7所示。IQGA寻优结果为σ=0.2。

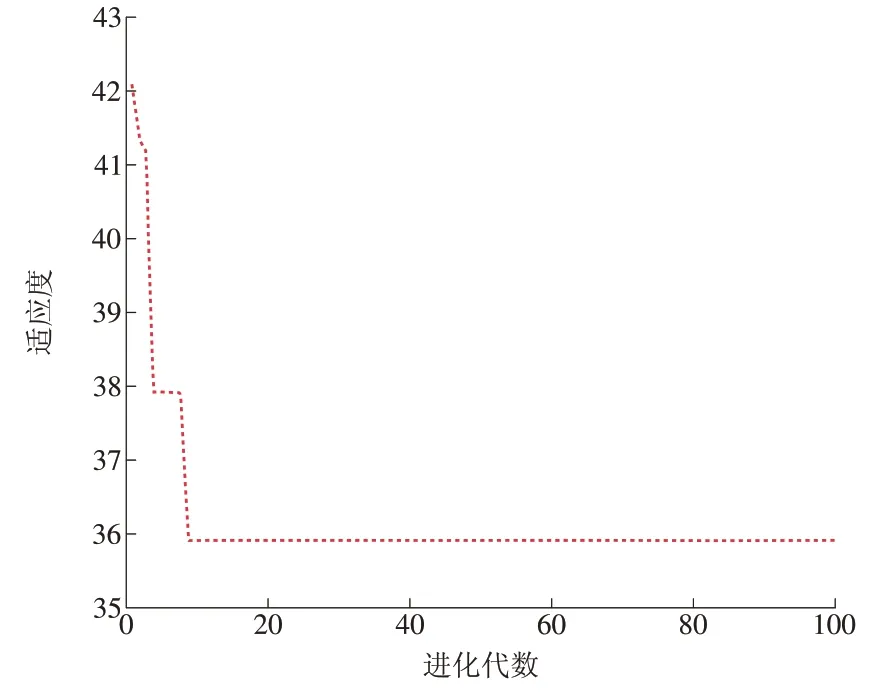
图7 最优个体适应度曲线Fig.7 Optimal individual fitness curve

将IQGA寻优后的σ值赋予GRNN网络，根据输入输出变量个数及维数，利用350组历史数据训练模型，从而完成模型建立。训练数据预测结果如图8所示。

图8 训练数据预测结果Fig.8 Training data prediction results

从预测结果看，IQGA预测误差较小，可用于后续的研究分析。基于以上模型，对现场数据中的后40个进行预测，为了充分检验该算法的性能，将本文所提出的IQGA-GRNN与GRNN，QGA-GRNN进行对比，其中GRNN寻优结果为σ=0.10，QGAGRNN寻优结果为σ=0.16，测试数据预测结果对比如图9所示。模型训练时间及误差对比结果见表2，其中Emax为实测值与训练模型之间的最大误差，Eave为平均误差。

图9 3种算法测试数据预测结果对比Fig.9 Comparison of predicted resultson test data by threealgorithms

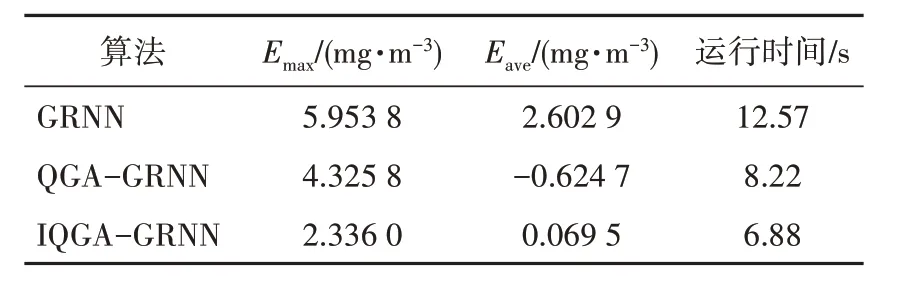
表2 3种算法测试数据预测误差对比Tab.2 Prediction errors of thetest data obtained by three algorithms

从图9可知，IQGA-GRNN训练模型的最大误差Emax为2.336 0 mg/m3，实测值与训练模型的最大误差控制在8%以内，平均误差只有0.069 5 mg/m3，在0.2%范围以内，且IQGA-GRNN运行时间更短，效率更高。由此证明，本文所提出的QGA-GRNN算法能有效预测脱硝出口NOx质量浓度。

4 结束语

烟气脱硝系统的非线性特点导致其机理建模较为困难，为此提出一种新的IQGA-GRNN建模方法，可用于变工况下出口NOx质量浓度的预测。应用改进量子遗传算法对广义神经网络中光滑因子进行寻优，使该算法逼近能力更强。针对现场实际运行数据，采用本文提出的IQGA-GRNN算法进行训练建模，并将该模型与GRNN模型、QGA-GRNN模型的预测结果进行对比，结果表明：IQGA-GRNN模型的预测值与实际值最大误差在8.0%以内，平均误差在0.2%以内，模型预测精度更高，是NOx质量浓度预测的有效方法。