基于TOPSIS法评价发电机组交易投机行为的研究
2021-06-03金骆松庞靖宇宋云鹏
何 洁,金骆松,赵 雯,庞靖宇,王 鑫,宋云鹏
(1.浙江电力交易中心有限公司,杭州 310016;2.浙江华云信息科技有限公司,杭州 310051)
0 引言
自《关于进一步深化电力体制改革的若干意见》(中发〔2015〕9 号文)文发布后,我国电力市场改革逐步深化,浙江电力市场的机制设计借鉴了美国PJM 电力市场的运营经验,中长期电力市场帮助市场主体规避现货市场的价格波动风险,采用双边协商、集中竞价和挂牌交易等模式提前锁定交易电量、电价;现货市场采用“日前市场+实时市场”的“两部制”市场机制,现货市场的交易品种包括电能量交易和辅助服务交易等。浙江电力市场体系较为复杂,对电力市场的规范可持续运营提出了严峻的考验。我国电力市场建设处于初级转型阶段,在多层次的市场结构下如何确保市场的公开透明,发现市场风险,促进市场的稳步健康发展是需要重点研究的课题之一。电力交易中心作为电力市场的运营机构,承担着组织市场主体交易、监测电力市场运行、评价电力市场运营情况等重要职责,如何发现市场漏洞、持续监测市场运行情况是交易中心的主要挑战。
发电企业是电力市场参与主体中的重要一员。纵观国内外电力市场,发电侧具备运用市场力影响出清电价从而造成市场扰动的能力,在我国电力市场的起步阶段,市场电价超出期望的大幅波动会影响市场改革的进程。因此,交易中心需要对发电企业的申报投机行为进行重点监测,以发现发电侧主体在交易过程中的不规范申报行为,防范市场风险,促进市场的平稳过渡。
1 TOPSIS 法原理
TOPSIS 法运用多个指标、对多个方案进行对比较选择,该模型的核心是首先确定各项指标的最优值和最差值,运用加权欧式距离计算各不同方案与最优值、最差值之间的距离,由此得出最佳方案与各比对方案的靠近程度,以评价方案的优劣[1-5]。
对电力市场交易中的发电企业而言,评价发电机组的申报行为可以使用一组评价指标,根据选取的特定指标来评测其申报行为是否具有投机倾向,为发电机组的申报行为贴上标签[6-7]。TOPSIS 法根据计算出来的每个发电机组各指标赋分与理想值的相对距离得到发电机组申报行为的总体得分,数据计算相对简单,可以对电力市场参与交易的所有机组进行同步评价,评价指标不受限制,并且随着电力市场的不同发展阶段对评价指标进行横向扩展,具备在大数据分析中应用的条件,因此选取TOPSIS 法可以对发电机组是否进行投机交易进行有效评价。
2 评价发电机组投机行为的指标构建
在市场建设初期,市场交易电价无论对于政府、市场运营机构还是用电主体来说都是重要考量对象。为了防止电价大幅波动,需要防范发电侧主体在市场交易中过分投机而导致电价大幅上升。因此,如何评价发电侧主体是否投机是需要研究的重点。
本文选取发电机组申报行为中的平均申报电价、价格突变率、容量持留率、合约现货比这4个指标作为监测对象,综合运用TOPSIS 法建立发电机组指标评分矩阵,对矩阵数据进行正向化、标准化处理后,基于4 个指标的权重赋值计算各发电机组在交易申报过程中的得分,从而以定量的评分结果作为发电机组申报投机行为取向的评价依据,以便于交易中心掌握电力市场中各发电机组的申报行为,监督市场主体的交易过程,规范市场主体的交易行为,优化市场机制设计[8-9]。发电机组交易投机行为评价体系如图1 所示。

图1 发电机组交易投机行为评价体系
目标层:评价发电机组的申报行为是投机型还是非投机型。
准则层:发电机组现货市场申报量价曲线的平均价格记作平均申报电价Pd,发电机组报价的突变性记作价格突变率V,发电机组申报的持留情况记作容量持留率R,中长期合约电量与现货市场电量的比值记作合约现货比CS[10-11]。
方案层:在PJM 电力市场中选取10 个典型申报的发电机组,采用TOPSIS 分析模型计算各发电机组在市场申报中的得分。
(1)平均申报电价。
发电机组在电力交易过程中的申报价格偏离平均边际成本越多,则其投机性越高;反之,申报价格越接近平均边际成本,则其非投机倾向越强烈。设发电机组申报的第一段出力为Q1、报价为P1,对应的第t 段申报的出力为Qt、报价为Pt,则其申报的加权平均电价为Pd=(P1Q1+P2Q2+…+P1Qt)/(Q1+Q2+…+Qt)。
(2)价格突变率。
在电力交易的分段式报价中,交易规则规定机组申报曲线为非单调递减分段式曲线,基于发电机组的成本曲线特征和申报曲线特征,取发电机组申报电力-电价曲线中后一段电价与近邻的前一段电价的比值中的最大值记作该发电机组的价格突变率V,价格突变率反映了发电机组在申报行为中的投机性倾向。由于发电机组是进行阶梯分段报价的,发电机组的报价从低到高依次为P1,P2,…,P10。标记发电机组申报的各段电价突变程度为P2/P1,P3/P2,…,Pt/Pt-1。选取所有突变程度取值中的最大值,记为V=max{P2/P1,P3/P2,…,Pt/Pt-1}。
(3)容量持留率。
在非检修、故障受限等状态下,发电机组申报最大出力应该更接近其可调出力水平,但是如果发电机组想制造市场短缺的假象,会以此为契机来提升其在市场申报中的报价,从而推高市场电价,获取更大的收益。将发电机组的容量持留率记作R,容量持留率高的机组为投机型倾向机组,容量持留率低的机组为非投机型倾向机组。设发电机组的可调容量为S1,发电机组的申报容量为S2,R=(S1-S2)/S1,R 在[0,1]区间内波动。
(4)合约现货比。
借鉴金融市场的经验,如果发电机组从套期保值的角度考虑,其签订的中长期合约的电量与其现货市场的电量不会相差很大,否则其更倾向于利用中长期市场和现货市场之间的利差进行套利。将发电机组申报的中长期合约电量E1与现货市场申报电量E2之间的比值记作合约现货比CS,即CS=E1/E2。CS指标在电力市场初期应该在一个区间内,CS越偏离该区间的机组越具有投机倾向。
3 构造评价矩阵
3.1 指标权重
用1—9 表示重要程度,两两比较平均申报电价、价格突变率、容量持留率、合约现货比用于判断一个机组是否投机的重要程度[12-14],如表1所示。

表1 对比标度分值
分别两两对比各评价指标之间的重要程度,建立指标之间对比的标度矩阵W,如表2 所示。

表2 标度矩阵
对标度矩阵W 进行一致性检验:首先计算一致性指标IC=(λmax-N)/(N-1),其中λmax为矩阵W 的最大特征根,N 为矩阵W 评价指标数量;其次查找对应的平均随机一致性指标IR;然后计算一致性比例CR=IC/IR,如果CR<0.1,则可以判定判断矩阵的一致性是有效的,否则就需要修正判断矩阵直到达到有效标准。对应的平均随机一致性指标IR如表3 所示。

表3 IR 分值
第k 个评价指标的归一化权重为Tkj=akj/(a1j+a2j+…+anj),akj为矩阵W 第k 个指标在第j 列的标度值。对每一列矩阵分别计算其归一化权重,得到新的矩阵,对新矩阵的各行分别运用算术平均法、几何平均法和特征值法计算每个指标的权重。对比3 种方法计算出的指标权重,最后得到每个指标的权重。
3.2 决策评分
决策矩阵为X,决策矩阵的元素为f,决策评分步骤如下[15-18]。
(1)矩阵数据正向化处理。
首先对矩阵进行正向化处理,数值越接近最优值,则正向化之后该数据越大,反之正向化之后的数据越小。
①极小型指标转化成极大型指标,使得数据极大化。
②中间型指标转化成极大型指标。{fi}是一组中间型指标集合,该集合的最优数值为fbest,则正向化公式为:

③区间型指标转化成极大型指标。{fi}是一组中间型指标集合,该集合的最佳取值区间为[a,b],则正向化公式为:

(2)矩阵数据标准化处理。
假设需要解决某一决策问题,由矩阵X 构建标准化的决策矩阵Z′,其矩阵元素Zij′为:

其中的fij由决策矩阵X 给出:

式(5)、(6)中:n 为矩阵行数;m 为矩阵列数。
(3)构造规范化的加权决策矩阵Z。
Z 的元素Zij为:

式中:wj为第j 个目标值的权重。
决策矩阵Z 中元素Zij值越大表示方案越好,Zij值越小表示方案越差。
(4)确定理想解和负理想解。
假设决策问题有m 个目标值,n 个可行解,其中目标值为fj(j=1,2,…,m),可行解Zi=(Zi1,Zi2,…,Zim),i=1,2,…,n,其规范化后的理想解为Z+,负理想解为Z-。

(5)计算每个方案到理想解的距离Si+和到负理想解的距离Si-。
采用欧几里得范数来测度距离,任意可行解Zi到Z+的距离为:

同理,任意可行解Zi到负理想解Z-之间的距离为:

某一可行解相对接近理想解的相对接近度可以定义为:

因此,如果Zi是理想解,则求得Ci=1;如果Zi是负理想解,则求得Ci=0。判断目标越靠近理想解,Ci越趋近于1;反之,判断目标距离负理想解越近,Ci越趋近于0。
4 算例分析
4.1 评价指标权重
针对某个发电机组的投标行为,申报成本是一个整体性评价指标。平均申报电价指标与价格突变率指标相比介于同样重要和稍微重要之间;平均申报电价指标与容量持留率指标相比稍微重要;合约现货比是测度发电机组在两个市场间进行套利的重要指标,平均申报电价指标与合约现货比指标相比稍微重要;价格突变率指标与容量持留率指标相比介于同样重要和稍微重要之间;合约现货比指标与容量持留率指标相比同样重要;价格突变率指标与合约现货比指标相比介于同样重要和稍微重要之间。指标权重对比如表4所示。
根据表4 各指标权重对比建立一个4×4 的矩阵W:
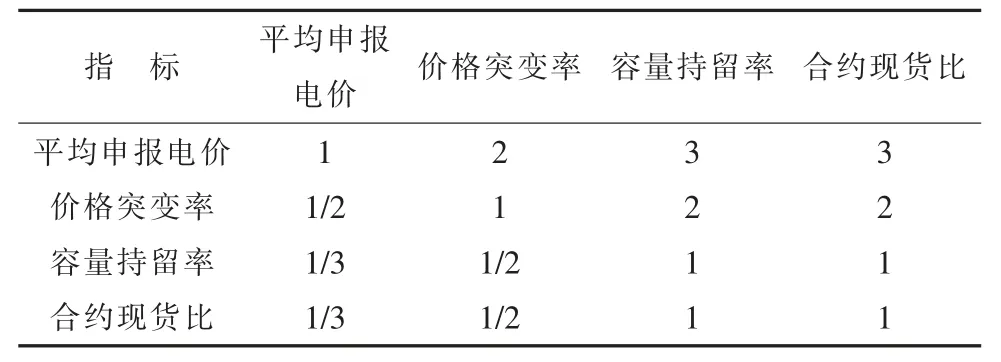
表4 指标权重对比

通过MATLAB 计算矩阵W 的一致性,得出一致性指标IC=0.037,一致性比例CR=0.041 6。矩阵W 的一致性比例CR<0.1,所以该矩阵的一致性是可以接受的。
对矩阵W 的各指标权重进行归一化处理,通过MATLAB 分别采用算术平均法、几何平均法和特征值法求得各指标的权重,如表5 所示。

表5 不同计算方法的指标权重
表5 显示,无论是采用算术平均法、几何平均法还是特征值法,计算出的4 个指标的权重基本一致。在后续模型分析中,采用特征值法计算结果作为4 个指标的权重赋值。
4.2 发电机组申报行为评分
以模拟电力市场中发电机组的申报数据(见表6)为例,对发电机组的申报行为进行综合评分,机组1—10 为10 个评价对象。未来各地区电力市场运营机构可以基于电力市场的实际运行数据,使用该评价方式对发电机组进行数据分析,以评价发电机组的申报行为。

表6 电力市场机组申报原始数据
根据美国Lazard 公司评估的美国各类能源发电的全生命周期平准化成本报告《Lazard’s Levelized Cost of Energy Analysis Version 13.0》,已经建成的传统煤电机组的边际成本区间为[26,41]美元/MW。设定:平均申报电价的最佳区间为[26,41]美元/MW;申报价格突变率的取值在(1,∞)范围内,数据越小越好;容量持留率的取值在(0,1)范围内,数据越小越好;结合某些地区电力市场交易规则,为了防止市场过度投机,中长期市场电量不超过实际电量的130%,实际电量低于合同电量80%执行更严格的偏差考核,因此设定合约现货比的最佳区间是(0.8,1.3)。根据最优值的取值范围对矩阵数据进行正向化处理,得到正向化后的数据矩阵(表7)。采用TOPSIS 法对上述矩阵数据进行标准化处理,得到标准化数据矩阵(表8)。
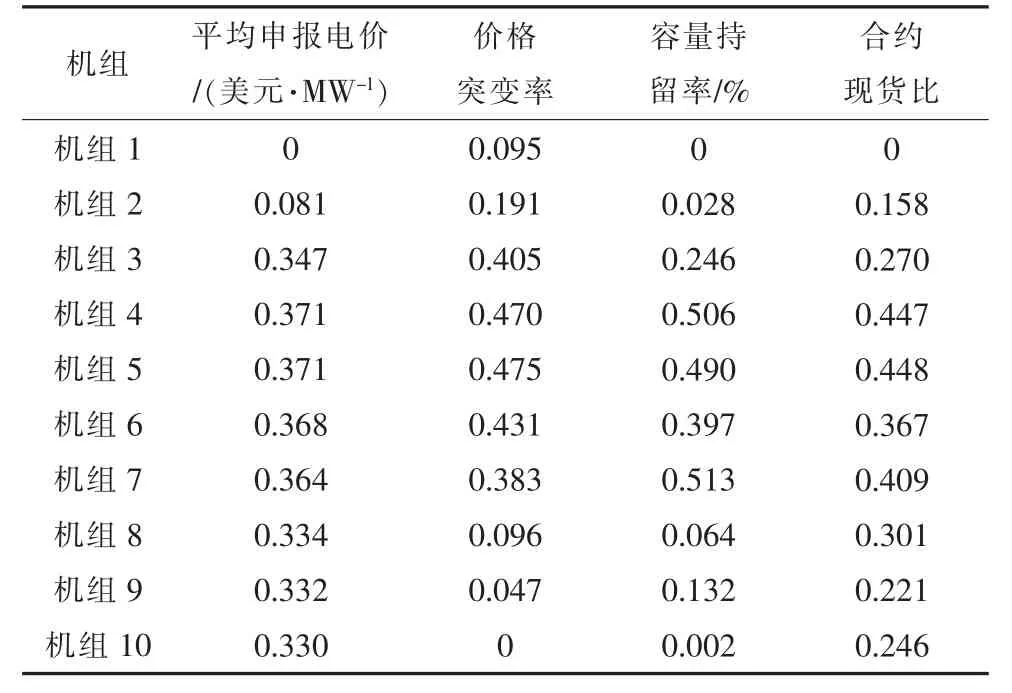
表8 机组申报标准化数据
4.3 发电机组申报行为计算分析
由表7 可得正理想解向量Z+=[0.371 3 0.475 2 0.513 2 0.447 6];负理想解向量Z-=[0 0 0 0]。

表7 机组申报正向化数据
综合各指标的权重赋值,分别计算各发电机组申报值与理想值的相对距离作为发电机组交易申报评价得分(表9),得到向量[0.106 5 0.282 70.729 1 0.991 8 0.980 1 0.870 4 0.888 8 0.493 6 0.469 8 0.429 4]。

表9 发电机组申报得分
可以看出,申报值越接近最优值的机组得分越靠近1,申报值越偏离最优值的机组得分越靠近0。
所有机组的得分都落在[0,1]区间内,根据该模型的评价标准,得分数据越大则代表该机组的非投机倾向越突出,因此得分落在[0.5,1]区间内的机组标签为非投机型,得分落在[0,0.5)区间内的机组标签为投机型。由此得到:在申报行为中归类为非投机型的机组包括机组3、机组4、机组5、机组6、机组7,归类为投机型的机组包括机组1、机组2、机组8、机组9、机组10。通过观察发现,投机型机组的申报指标确实偏离指标平均最佳评分较远,评价结果符合期望。
由此可见,运用基于权重的TOPSIS 模型可以有效评价发电机组申报行为的投机性,未来随着浙江电力市场的深入改革,可以逐步改变变量指标和各指标的权重[17],以实现对发电机组申报行为的有效评价。
5 结语
本文构建了一种基于TOPSIS 法评价发电机组申报行为的分析方法,首先构建了对发电机组申报行为进行评价的4 个指标,分别是平均申报电价、价格突变率、容量持留率、合约现货比,并对4 个指标建立矩阵进行权重赋分;其次基于美国PJM 电力市场发电机组的申报数据,运用TOPSIS 法建立矩阵,结合各评价指标的权重赋值对每个发电机组的报价行为进行定量计算评分,依此评价发电机组的申报行为;最后对发电机组的申报投机行为进行标签,得分落在[0.5,1]区间内的机组标签为非投机型,得分落在[0,0.5)区间内的机组标签为投机型。
该评价方法基于PJM 电力市场的申报数据,结合浙江电力市场的运行机制进行申报行为评价模型设计,对浙江电力交易中心监测市场主体(特别是发电侧)的申报行为进行评价,以发现市场主体不规范的申报行为,优化市场交易机制,修订市场交易规则,确保市场的平稳健康发展。未来随着浙江电力市场的纵深发展,可以综合考虑浙江中长期电力市场和现货市场的交易品种设计以及交易模式的演进,对评价指标进行优化设计,并修改相应的评价标准,以期能够适应浙江电力市场的发展方向。
