连续比例逻辑斯蒂回归模型在半参数ROC 曲面估计上的应用*
2021-06-03杨朝伟
杨 朝 伟
(南京财经大学 应用数学学院,南京 210023)
0 引 言
诊断试验在医疗保健中起着非常重要的作用。它可以通过对患者的症状、体征以及各种检查结果来判断患者得了哪些疾病,同时也能判断患者未患哪些疾病,而在诊断试验中很重要的一环就是诊断试验准确度的研究。诊断试验准确度简单地说就是在诊断试验中区分不同疾病状态的能力,评价诊断试验准确度有很多指标,比如优势比和Youden指数等。
1971年,Lusted[1]提出了一种新的评价方法即ROC曲线,这是一种用来评价有两类诊断结果(阳性、阴性)的诊断试验准确度的方法,它有很多的优点:首先,ROC曲线呈现了可视化的诊断准确度;其次ROC曲线也不需要选择一个特殊的决策阈值,同时也不受患病率的影响。此外,根据Campbell[2]的研究,它也不受试验结果量纲的影响,也就是说对试验结果作单调变换,如线性、对数变换,ROC曲线不发生变化。因此在提出之后,ROC曲线就成为评价两类诊断结果准确性最常用的方法。
但是在实际中,经常会碰到有3种或3种以上诊断结果的情形,这使得传统的ROC曲线评价方法不再适用。因此,近年来,学者们开始将研究重心从ROC曲线转移到ROC曲面上来,以应对有3种或3种以上诊断结果的情形,相关的研究也已有大量成果出现[3-8]。当诊断结果有3类时,可以将被测对象分为3类,记测量数据为X,任意给定两个临界值α1,α2且α1≤α2,将满足X≤α1的对象判定为第一类,将满足α1≤X≤α2的对象判定为第二类,剩余的判断为第三类。Nakas,Yiannoutsos[3]基于ROC曲线的定义提出以Tα2对Tα1和Tα3作图得到的曲面为ROC曲面的定义,这里的Tαi为将第i类的对象正确判别为第i类的概率,i=1,2,3;同时还提出了以ROC曲面下的体积作为诊断试验准确度的评价指标,体积越大,诊断测试方法就越准确。
本文将提出一种半参数方法用来对一个有3类结果的连续型诊断测试进行ROC曲面分析,这也是Nakas,Yiannou-Tsos[3]和Xiong[4]研究的情形,不过他们使用的是参数方法和非参数方法,本文研究的是半参数方法。该方法的核心思想是在一个半参数密度函数比模型下进行ROC曲面的构建,在一些文献中,半参数密度函数比模型已经成功运用到了ROC曲面的分析研究中,如参考文献[9],文中所使用的模型是比例优势模型,而本文使用的模型是连续比例逻辑斯蒂回归模型,并且使用连续比例逻辑斯蒂回归模型得到的结果十分优良,计算也很简便,运用一些逻辑斯蒂软件即可得到结果。
1 主要方法
令D=k表示第k类,k=1,2,3,对一个给定的测试结果X=x,连续比例逻辑斯蒂回归模型有如下形式:
其中:m=1,2,α1和α2是尺度参数,β1和β2是pxl的向量参数,r(x)是一个关于x的pxl光滑方程,在大部分应用中r(x)=x或者r(x)=(x,x2)T,在连续比例逻辑斯蒂回归模型中:
因为
P(D=1|X=x)+P(D=2|X=x)+P(D=3|X=x)=1
可得
从而
这里的i=1,2,3。
由贝叶斯公式可得
因此
令Fk(x)=P(X≤x|D=k),k=1,2,3,fk(x)是Fk(x)的密度函数,k=1,2,3,有
exp(θk+gk(x;η))
其中
为了保证模型可辨识,将α1和θ1合并,容易得到如下的三样本半参数密度比模型:
X31,…,X3n3~f3(x)
Xk1,…,Xknk~fk(x)=exp(θk+sk(x;η))f3(x),k=1,2
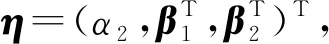
sk(x;η)=
以{T1,…,Tn}表示合并的样本:
{X11,…,X1n1;X21,…,X2n2;X31,…,X3n3}
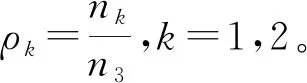
这里的Pi=dF3(Ti),i=1,…,n是概率的跃迁且总和为1,与Qin,Zhang(1997)[9]类似,L在受到如下的约束条件的情况下:
这里k=1,2。
L的最大值可以通过拉格朗日乘数法在

l(θ,η)是剖面对数似然函数,且
注意到,约束条件:
等价于
这说明exp{θk+sk(Ti;η)}dF3(t)是一个分布函数。
因此F3(t)的半参数最大似然估计是
类似地,Fj(t),j=1,2的半参数最大似然估计是
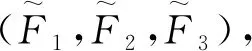
这里的s1,s2∈[0,1]。用
j=1,2
从而得到ROC曲面估计值为

2 实例分析
实例的数据来源于Reaven,Miller[11]进行的一项糖尿病研究。在该数据中,145名非肥胖成年人被分为3个人群,其中76人正常,36人为糖尿病前期,33人为显性糖尿病。以空腹血糖(PLG)为例进行ROC曲面分析。由于原始数据在量级上变化很大,因此对数据进行对数变换。此外根据Qin,Zhang[10]的相关研究,发现模型在r(x)=x时拟合得比较好,代入后拟合的结果为α2=43.393 0,β1=-3.350 4,β2=-4.825 1,θ1=0.020 7,θ2=-16.688 2。对ROC曲面进行估计时,以R(0.2,0.4)为例,得到的估计值为0.939 8,相应的95%置信区间为(0.878, 0.984)。对于VUS的分析,其估计值为0.686 6,置信区间为(0.587,0.789)。此外也得到了使用非参数方法构建的ROC曲面和使用半参数方法构建的ROC曲面。如图1,图2所示:
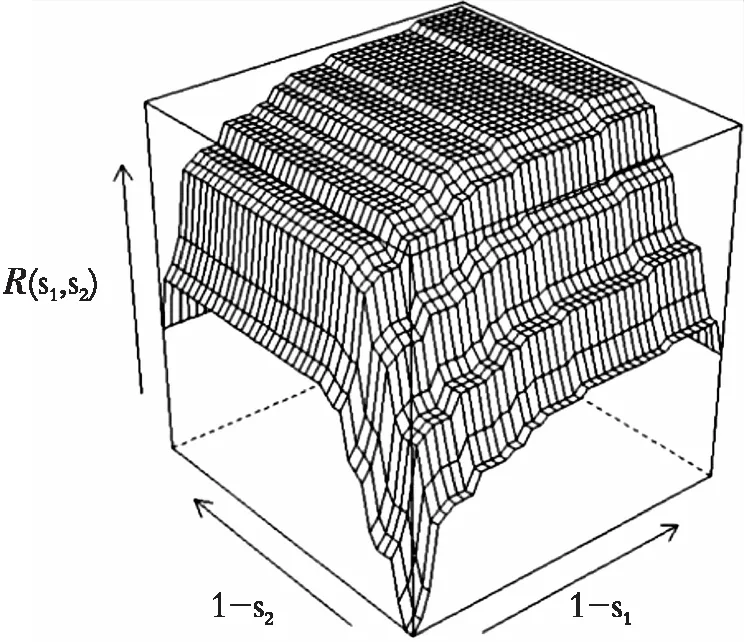
图1 基于实例的非参数ROC曲面估计值Fig. 1 Non-parametric ROC surface estimators based on the real example
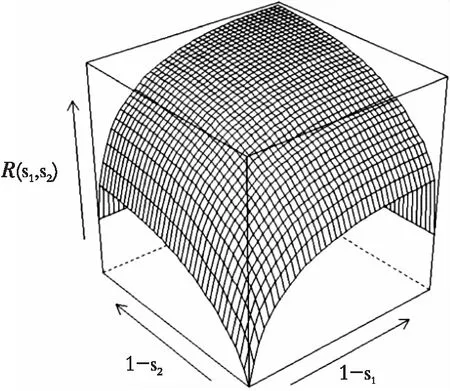
图2 基于实例的半参数ROC曲面估计值Fig. 2 Semi-parametric ROC surface estimators based on the real example
从图1和图2可以看出,图2中的半参数ROC曲面要比图1中的非参数ROC曲面更加光滑,这说明了半参数方法要比非参数方法更优越。此外,若用非参数方法对有序数据进行ROC曲面分析,虽然不需要进行任何的分布假设,但是估计非常粗糙,当数据分布不佳时,体积的估计值将严重低于实际ROC曲面下的体积,因此在估计ROC曲面时,更适宜用半参数方法。
3 结 论
将连续比例逻辑斯蒂回归模型与半参数方法相结合,提出了一种bootstrap方法来构造ROC曲面的置信区间,并得到了ROC曲面估计量的表达式。相比于非参数方法,用半参数方法得到的ROC曲面更平滑,得到的结果也更精确。此外在计算半参数最大似然估计时,传统的方法是利用牛顿迭代法之类的数值计算方法,而这里是用一些逻辑斯蒂回归程序,这样可以很快速地得到结果,因此方法也更容易实现。但在实际应用中还存在着一些不足,这是因为由于缺少相应的软件,半参数方法相比于参数或非参数方法对于部分曲面下体积估计的有效性和稳健性还没有学者进行评价。
