基于改进的Park变换的UPQC综合检测方法研究

孙标志， 高 昕， 周 聪

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

0 引 言

随着工业自动化程度的不断提高和电子技术的不断向前发展，电力系统中各种非线性负载使得电能质量问题更加突出[1]。针对这个现状，日本学者H.Akagi于1996年首次提出了统一电能质量调节器(UPQC)的概念，它结合了串联和并联补偿器的优点，除了能够补偿非线性负载引起的谐波和无功功率之外，还可以对三相电网的畸变量、不平衡等一些问题进行补偿，具有综合补偿以及调节电能质量的功能，因此UPQC成为改进电能质量(PQ)最具吸引国内外学者的研究方案。电压、电流的补偿量检测，进而对其控制是UPQC装置的两个重要组成部分，因此，检测方法能否精确得到电压以及电流的补偿量具有重要的研究意义[2-3]。

目前，应用广泛的检测方式仍然是基于瞬时无功功率理论的检测法。文献[4]分析了p-q检测法，但电力系统在实际运行过程中，网侧电压波形往往会发生畸变，使得到补偿量有较大误差；文献[5-6]分析ip-iq检测法，虽不受电压畸变影响，但对于锁相环具有更高的要求；dq检测法虽然不受电压畸变与不对称的影响，但是由于锁相环(PLL)的存在，也会造成一定的误差。文献[7]提出了UPQC的电压分量检测法，它是基于三相中的某一相的电位为基准，然后令其向后偏移120°和240°，但缺点是仅在稳态补偿当中使用。文献[8]提出了对称分量法得到基波正序电压瞬时相位，但没考虑谐波会对检测造成影响。

由于锁相环在检测中造成误差，提出给变换矩阵中的角频率一个固定值，避免使用锁相环；针对低通滤波器(LPF)造成响应时间的延迟，引起一定的误差，提出了将改进的平均值滤波与低通滤波器(LPF)串联，基于Matlab/Simulink平台搭建模型，仿真分析了改进后的检测方法，并于传统的检测对比，在三相电压畸变且不平衡时，验证了所提方案能实时精确的得到电压电流的补偿量。

1 UPQC基本结构[2]

UPQC的基本结构如图1所示，串联变流器经变压器与三相电网相连，将其看作受控电压源，主要补偿输出电压，由此使三相负载侧的电压为额定电压；并联变流器看作受控电流源，补偿非线性负载的谐波以及无功电流等。串联和并联变流器的直流侧由公共的直流母线电容Cdc连接起来；滤波器为LC滤波器，是用来抑制串联变流器高频开关产生的纹波，滤波器2为L滤波器，作用是抑制并联变流器输出电流产生的纹波，图1中uS、uc、uL分别代表电网侧电压、串联变流器输出的补偿电压以及负载侧电压。

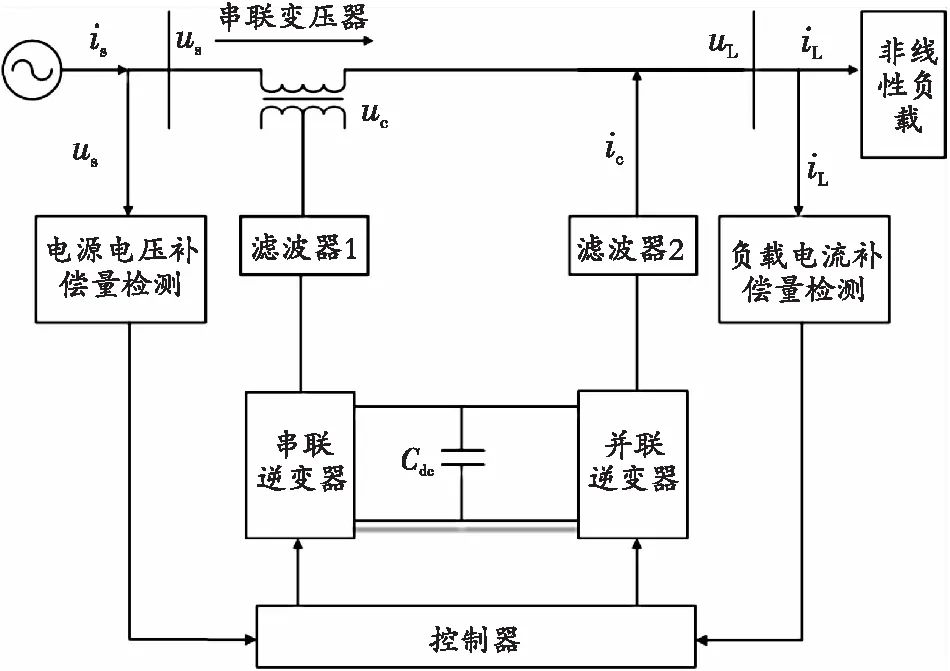
图1 UPQC基本拓扑结构图Fig. 1 Basic topological structure diagram of UPQC

2 基于改进的Park变换检测法

2.1 Park变换检测法

假设系统中三相电压发生畸变且不对称时，可将三相正序、负序、零序以及谐波分量作如下表示(以A相为例)：

(1)

(2)

其中，ua+、ua-、uz表示三相电压的基波正序、负序、零序分量；Un+、Un-分别表示为三相电压第n次谐波的正序、负序分量的幅值；φn+、φn-分别表示为三相电压第n次谐波的正序、负序分量的初相角，n是正整数。

通过同步坐标变换(Synchronous Reference Frame Transformation)将abc坐标系下的三相电压usa、usb、usc变换到d-q坐标系下，结果如下：

(3)

(4)

则变换后的三相电网电压表示为

(5)

由式(5)可得，a-b-c坐标系下的第n次三相正序电压在dq轴的分量变为角频率为(n-1)的交流分量；第n次三相负序电压在dq轴上的分量变为角频率为(n+1)的交流分量，只有基波正、负序分量在dq坐标系中表现为直流量，为udf、uqf，其余各分量仍然保持交流量[9]。因此，可以得到基波正序电压初始相位角的信息，结果如下：

(6)

设电压基波正序分量的幅值是Um、初相角为φu，在实际的三相电网中，会有一定的电压和线路损失，因此得到基波正序电压的幅值信息，令它与电网额定电压幅值相等，因此基波正序电压结果如下：

(7)

然后将所得到的基波正序电压从实际电压去除便可得到电压的待补尝量，同时将dq坐标系按逆时针旋转一个角度φu，新的d′q′坐标系下得到基波正序有功电流ifp，如下：

(8)

实际的三相电网中，对于UPQC装置，需要同时补偿负载端电流的无功分量、非对称分量和谐波电流。因此，只考虑基波正序有功电流，然后与实际的三相负载电流进行差值，得到并联侧的补偿电流指令。

2.2 预设变换矩阵频率

从上述同步旋转坐标变换的原理中，需要确定dq变换矩阵中的角频率。在传统的检测方法中，一般是通过锁相环来获取变换矩阵中所需要的角频率，以此来确定正弦信号以及余弦信号。虽然使用锁相回路可以获得电压或三相电流的基本频率和初始相位角，但是通常会影响检测的准确性，而且由于利用锁相环增加了电路板面积，使其在设计以及调试等方面变得更为复杂。因此在同步旋转坐标变换的综合检测法的基础之上，通过预设变换矩阵中的角频率[10]，使检测电路更为简洁、灵活，具体的分析如下：

在实际的电网中，由于电网的频率不会一直稳定在50 Hz，可能会出现波动、频率偏移等一些情况，因此会产生一些不可避免的误差，又或是因为在离散变换过程当中，电压或电流信号的每周期采样数与正余弦表序列数有差异。因此假设dq变换矩阵中的频率为ω0，基波频率为ω1，系统中三相电压表达式仍如式(1)所示。

则三相静止的静止坐标系经同步旋转坐标变换后，在dq坐标系下的表达示为式(9)：

(9)

根据GB/T15945-1995《电能质量电力系统允许偏差》的相关规定，供电系统正常运行时允许的频率差值为0.2 Hz，当系统容量偏小时，允许的差值可以放宽至0.5 Hz。由于我国的电网工频为50 Hz，则：

|ω-ω0|=|2π(f-f0)|≤|2π(50±0.5)-50|=π

由此可知在实际的电网中，电网的频率偏差是很小的，不会出现很大的变化，电网基频与dq变换矩阵中的频率一般不会相差1 Hz，因此同样对上述的变换结果经过低通滤波器后得：

(10)

由式(10)可以看出，此时所得到的分量并不是直流分量，而是频率很低的交流量，对其进行dq反变换，如下：

(11)

由式(11)得到，反变换后的电压频率与电网电压的基频相同，因此说明dq变换矩阵中的频率只在变换过程中起作用，并不会对最终获得的电压基波分量造成影响。直接设变换矩阵中的角频率为100π，使检测电路得到了简化。

2.3 电流平均值滤波法

传统的ip-iq检测法和dq检测法，由同步旋转坐标变换的三相电压或电流需要经过低通滤波器对其信号进行处理，而在实际应用中，低通滤波器的种类、阶数和截止频率都对滤波效果有着很大的影响。

根据平均值滤波的原理，因为交流分量的波形相对于横轴对称，其在一个周期时间T内的平均值为零，因此，在三相电压或电流通过平均值模块进行滤波之后，在周期时间T内只有电压或电流的直流分量[11]。

由平均值理论的原理，其如式(12)所示：

(12)

经过平均值滤波后，得到了与基波分量相对应的直流分量，与之传统的低通滤波器相比，平均值滤波法在动态响应以及准确性都得到了改善，而且平均值滤波法更能应用在数字系统中。根据式(12)需在一个基波周期T中对输入量执行积分运算，因此使得三相电压、电流在进行谐波检测时的实时性会较差。

2.4 改进电流平均值滤波法

以不对称的三相负载电流进行分析，如下所示(A相为例)：

(13)

通过同步旋转坐标变换将三相电流变换到dq坐标系下，变换后的三相负载电流用id、iq表示，结果如(14)所示：

(14)

选用UPQC的非线性负载为带阻感的三相不可控整流桥，其产生的谐波电流次数主要是5次、7次、11次、13次……，n=6k±1次谐波。其中k为整数，当k=0时，n=1。代入式(14)可以得出，各次交流分量都是偶数分量，因此将积分周期在每个偶次交流分量的最小公倍数上进行定义，也就是将T/2设为运算的积分周期。

因此，改进后的平均值方法如下：

(15)

但是，这不可避免地会影响补偿量检测的响应速度，因此，在以T/2为周期的平均值滤波器的基础之上提出将低通滤波器与其串联，其中LPF起到消除三相电压或电流中的奇次谐波成分的作用，因此串联的低通滤波器应采用最低的奇次频率，也就是三次谐波，150 Hz，原理图如下：

图2 改进的平均值滤波原理图Fig. 2 Improved average filter schematic diagram

以仿真为例，三相电源电压的初始幅值为380 V，频率为50 Hz，负载为三相不可控带阻感的整流桥，其中R=10 Ω、L=30 mH。在系统刚运行时加入10%的5次谐波和8%的7次谐波，运行0.3 s。分别选取传统的与改进的平均值滤波法对经同步旋转坐标变换后的d轴电流进行交流分量的滤波处理，仿真结果如图3所示：

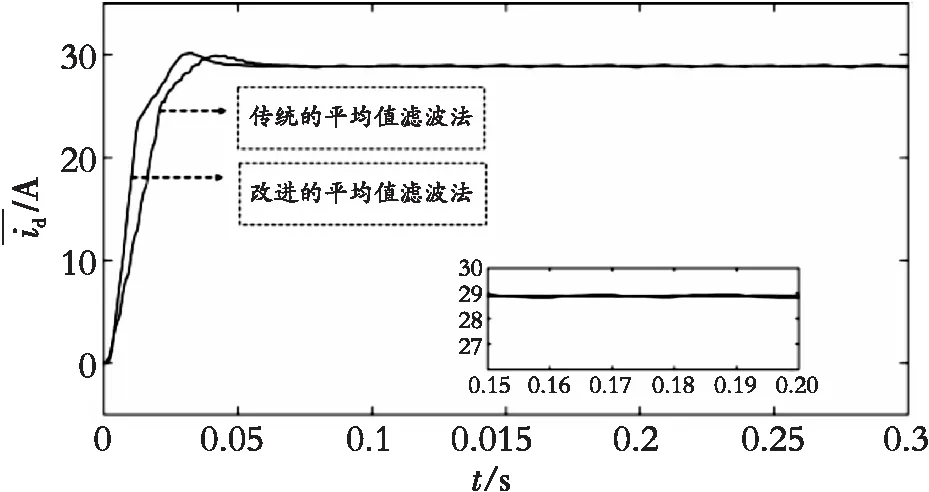
图3 改进的平均滤波器波形对比Fig. 3 Comparison of improved average filter waveforms

由图3可以看出它们应对冲击电流时都有较好的抑制效果，但传统的平均值滤波法因为是在一个基波周期T内对输入量进行积分运算，因此得到的直流分量的时间较长，约为0.06 s；而改进的平均值滤波法在0.04 s后便可得到稳定的直流分量。在0.15 s时，滤波器获取的直流分量已经达到了稳定的状态，都获得了相对稳定的直流分量，对应的谐波几乎全部滤除。

图4、图5分别是传统的平均值滤波法与改进的平均值滤波法得到的电流基波波形图与其对应的FFT分析。

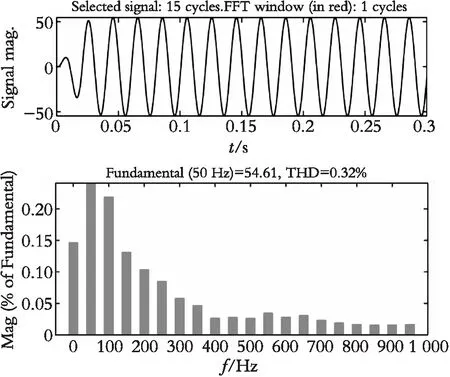
图4 传统均值滤波法的基波电流及FFT分析Fig. 4 Fundamental current and FFT analysis of traditional mean filtering method

图5 改进均值滤波法的基波电流及FFT分析Fig. 5 Fundamental current and FFT analysis of improved mean filtering method

由图5可以看出:串联改进型的平均值滤波法比传统的平均值滤波法的畸变率要小，也验证了传统的低通滤波器与平均值滤波法串联有着更加精确的基波波形图，其得到的直流分量波形满足了改进的精确性的要求。

3 仿真分析

根据上述分析，给出了改进之后的UPQC综合检测的原理框图，如图6所示。

为了验证所提出的改进的综合检测法在三相不对称系统中能否准确得到电压电流的补偿量，因此在三相电网电压不对称且发生畸变的情况下进行仿真。整个系统仿真运行时间为0.3 s，其他参数不变。在0.05 s～0.15 s电压跌落20%，0.15 s～0.25 s电压升高20%，整个过程注入10%的5次谐波和8%的7次谐波。

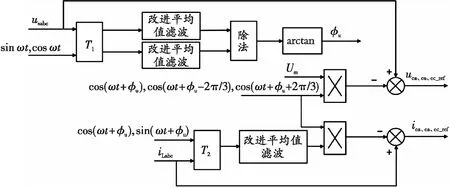
图6 改进电压电流综合检测法原理框图Fig. 6 Principle block diagram of improved voltage and current comprehensive detection method

图7为电压骤升、骤降且加入10%的5次谐波和8%的7次谐波后的三相电网电压波形。

图7 三相电网电压波形Fig. 7 Three-phase grid voltage waveform

图8为经过改进后的平均值滤波后得到的三相电网电压基波波形。

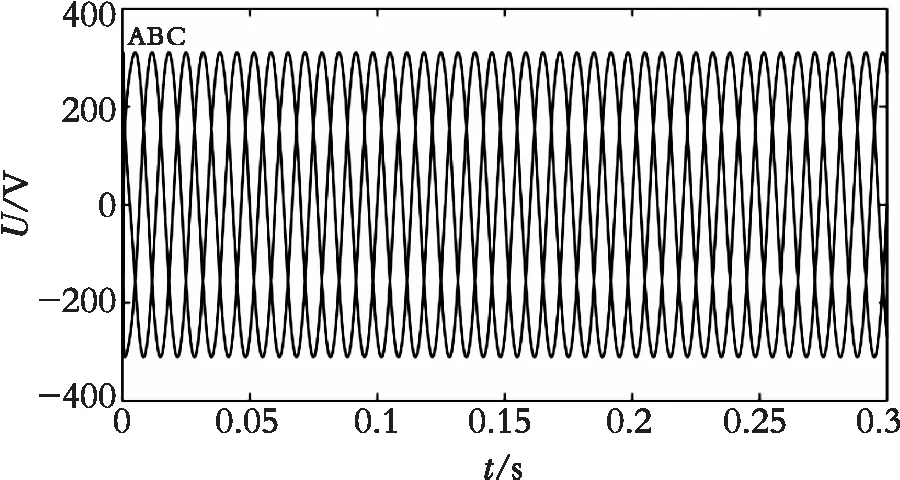
图8 三相电压基波电压波形Fig. 8 Three-phase fundamental wave voltage waveform

图9为经过改进后的平均值滤波后得到的三相负载电流基波波形，由此可看出，改进后得到的基波波形符合实时性、精确性的要求，且与基波电压波形保持同相位的关系，为后续控制器进行谐波补偿创造了前提；图10、图11分别为电压、电流的补偿量波形(均以A相为例)，可看出，滤除谐波分量的响应速度和精确性符合改进后的平均值滤波法的要求。

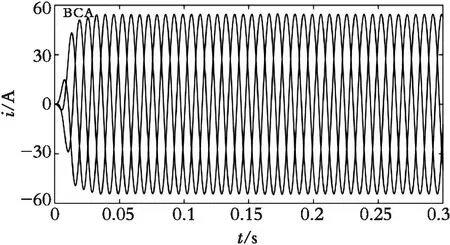
图9 三相负载基波电流波形Fig. 9 Three-phase load fundamental wave current waveform

图10 A相补偿电压波形Fig. 10 A phase compensation voltage waveform

图11 A相补偿电流波形Fig. 11 A phase compensation current waveform

4 结束语

介绍了基于Park变换的电压电流综合检测法，在此基础之上，结合了提出的dq变换矩阵中固定的角频率，使检测过程更为简洁方便，针对低通滤波器不可避免的延迟问题，在传统平均值滤波法的基础上，提出了将平均值滤波器与低通滤波器串联起来，通过仿真模型的波形可以看出，在三相电压不平衡且发生畸变时，相比传统的检测法能很快滤除谐波，得到相应的基波分量，符合快速性、准确的要求。