履带移动平台带边界层bang-bang路径跟踪控制
2021-06-02吴明阳李小波代嘉惠雷世威潘长松薛春荣
吴明阳, 李小波, 代嘉惠, 雷世威, 潘长松, 薛春荣
(中煤科工集团重庆研究院有限公司, 重庆 400037)
0 引言
煤矿机器人是煤矿智能化的重要载体,研发和应用煤矿机器人是实现煤矿无人化的重要途径[1]。国家煤矿安全监察局发布的《煤矿机器人重点研发目录》建议将机器人纳入煤矿重点科技专项范围[2],以提升煤矿智能化水平,逐步实现煤矿少人及无人化。
路径跟踪控制是实现煤矿机器人自主导航行走的关键技术之一。当完成规划任务后,需要利用跟踪算法计算机器人执行器目标输入,以保证机器人跟踪预定的路径[3]。现有的机器人路径跟踪算法包括纯追踪算法[4]、滑模控制算法[5-6]、模型预测控制算法[7]等。其中纯追踪算法简单、直观,控制参数少,在低速场合跟踪效果良好,因此,成为当前移动机器人导航和控制中广泛应用的路径跟踪算法之一[8-9]。前视距离是影响纯追踪算法跟踪精度的重要因素,为实现前视距离的自适应调整,李逃昌等[10]提出基于模糊理论调整纯追踪算法的前视距离;李革等[11]通过定义以速度和弯度为自变量的函数,实现前视距离调整,平均跟踪误差为0.077 m。
已有的路径跟踪算法均需采集机器人两侧驱动轮转速作为反馈量进行转速闭环控制,对于开关阀控制不可闭环调速的液压履带移动平台并不完全适用。由于成本、加工难易度及用户喜好等因素,开关阀控液压履带移动平台在矿业、农业、军工等领域应用十分广泛。目前,在掘进机[12]、钻孔机[13]、喷浆机[14]等大中型煤矿机械中均大量使用该类型底盘。因此,研究开关阀控履带移动平台的路径跟踪控制对于提高煤矿机械智能化水平具有重要意义。
针对开关阀控履带移动平台路径跟踪问题,本文借鉴纯追踪算法的思想,提出一种基于航向角偏差带边界层的bang-bang路径跟踪控制算法,并通过李雅普诺夫稳定性定理分析了边界层内外系统状态的稳定性;通过仿真验证算法在不同前视距离下对矩形目标路径的跟踪效果,并与纯追踪算法进行对比,分析两者的路径跟踪性能差异;最后,在试验样机上对bang-bang控制算法进行了地面试验。
1 履带移动平台路径跟踪控制模型
定义导航坐标系为xoy,由于平台速度较低,忽略纵向滑移和侧向滑移,假设重心与几何中心重合,则履带移动平台点追踪简化运动学模型如图1所示。图1中,(x,y)为平台实时位置;(xr,yr)为当前时刻追踪的目标路径点;θ为航向角;θerr为航向角偏差;ρ为当前位置和目标路径上目标点的距离;r为纯追踪算法转弯半径;l为纯追踪算法前视距离;a,b分别为机器人局部坐标系下前视点到机器人几何中心的侧向距离和纵向距离;d=r-a;Δx,Δy分别为全局坐标系下目标路径点到平台当前位置的距离在x,y方向的分量。
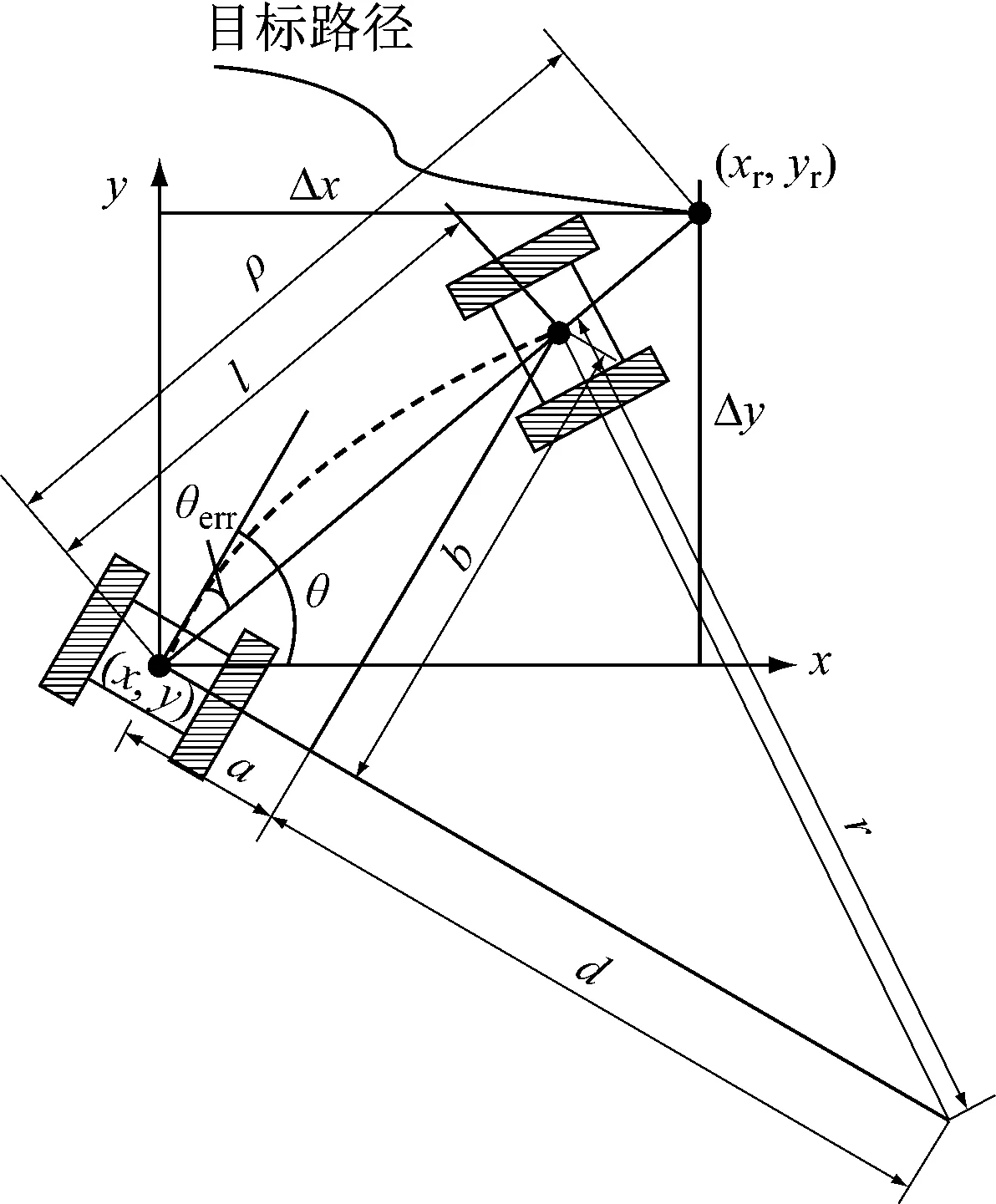
图1 履带移动平台点追踪简化运动学模型Fig.1 Simplified kinematics model of point tracking for crawler mobile platform
履带移动平台的动力学响应可近似为一阶环节,定义ρ、θerr、速度v及航向角速度ω为状态变量,根据几何及运动学关系得到点追踪模型[15]:
(1)
式中:Tv和Tω为一阶系统时间常数;uv和uω分别为速度及航向角速度的虚拟控制输入。
定义左右两侧履带线速度为vl和vr,则其与虚拟控制输入的关系为
(2)
式中h为履带间距。
2 履带移动平台路径跟踪控制算法
2.1 纯追踪算法
纯追踪算法是一种几何控制算法,可模拟人驾驶车辆行为对平台进行控制。纯追踪算法仅包含前视距离l一个可调参数,在平台运动过程中,平台将依据自身位置和目标路径搜寻目标路径前进方向上不小于前视距离且与前视距离最接近的离散路径点作为目标点,然后基于几何关系获得目标曲率。设目标曲率为γ,根据图1可得
(3)
因为sinθerr=a/l,所以,式(3)可写为
(4)
从式(4)可看出,纯追踪算法本质上是依据航向角偏差进行控制,算法以前视距离l作为调整参数,选择较大的l可使跟踪平稳,但收敛时间变长;选择较小的l可提高跟踪精度,但l过小可能造成振荡甚至不稳定。
定义速度控制输入为uv=v2,结合式(4)可得到航向角速度输入量:
uω=v2γ
(5)
在获得虚拟控制量uv和uω后,利用式(2)可得到履带的目标速度。根据式(2),纯追踪算法需要通过控制两侧履带速度得到虚拟控制量uv和uω,但是开关阀控履带移动平台两侧履带不可闭环调速,因此,纯追踪算法无法直接在开关阀控履带移动平台上应用。
2.2 bang-bang控制算法
bang-bang控制又称继电控制,适用于开关控制输入系统,便于编程实现及调试,参数校准及调整简单,在航天、液压等领域均有应用。bang-bang控制属于变结构控制,可在2种状态之间切换,开关阀控履带移动平台的控制信号包含开、关2种状态,因此,本文基于航向角偏差,利用bang-bang控制实现平台的路径跟踪。

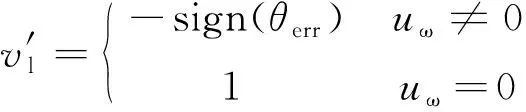
(6)
(7)
根据式(5),uω的符号与v2和γ有关,由于vr=uv>0,故sign(uω)=sign(γ)。根据式(4),由于前视距离l>0,故sign(γ)=sign(θerr)。综上可得,sign(uω)=sign(θerr),故式(6)、式(7)中uω可以用θerr替换:

(8)
(9)
由于存在扰动或传感器噪声,式(8)、式(9)会造成电磁阀频繁切换。为减小扰动对系统的影响及电磁阀切换频率,借鉴滑模控制中减小抖振的方法,引入边界层,则控制律修改为

(10)
(11)
式中ε为边界层厚度,rad,0<ε≪π/2,ε越大,电磁阀切换频率越低,但跟踪精度也会下降。
在实际应用中,应在保证满足跟踪精度要求的前提下,选择较大的ε,以保护执行器。
对于开关阀控制履带移动平台,其两侧履带的线速度大小近似相等,即vl≈vr。因此,根据式(2)可得到在式(10)、式(11)作用下的虚拟控制输入:
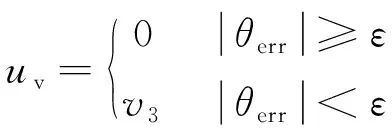
(12)
(13)
式中:v3=(vr+vl)/2;ω0=2(vr+vl)/h。
从式(12)、式(13)可知,当航向角偏差超过边界层时,移动平台通过原地转向调整姿态,从而减小航向角偏差;当航向角偏差在边界层之内时,平台朝目标点直线行驶。因此,该算法适用于直线或折线目标路径。
3 稳定性分析
稳定是控制系统的重要性能,也是系统能够正常运行的首要条件。控制系统在实际运行过程中,会受到内外因素的扰动。如果系统不稳定,任何微小的扰动作用都将导致系统偏离原来的平衡状态,并随着时间发散。因而,分析闭环系统的稳定性,是控制理论的基本任务之一。李雅普诺夫稳定性理论[16]是控制领域判断系统稳定性的普遍理论,不仅适用于单变量、线性、定常系统,对于多变量、非线性、时变系统同样适用。由于本文中的闭环控制系统为非线性系统,证明其李雅普诺夫稳定性,可判断当系统状态在平衡点邻域内不会发散,即航向角偏差、到目标点的距离等关键状态会收敛至原点附近的邻域内,从而保证路径跟踪正常运行。
根据式(12)、式(13),在路径跟踪过程中存在原地姿态调整和直线行驶2种动态过程,2种动态过程根据θerr的值进行切换。下面分别讨论2种动态过程中闭环系统的稳定性。
3.1 原地姿态调整过程中的稳定性
移动平台在原地调整姿态下,|θerr|≥ε,将式(12)、式(13)代入式(1),得
(14)
定义该过程初始时刻速度v(0)=v0,v在原点渐进稳定,其解为
v=v0exp(-t/Tv)
(15)
式中t为时间。
将式(15)代入式(14),消去v,得
(16)

(17)
基于李雅普诺夫稳定性理论分析简化后状态空间模型的稳定性,得出如下结论:当|θerr|≥ε时,在式(12)、式(13)的作用下,Tω>0且ω0>0时,系统在原点是李雅普诺夫稳定的。下面对该结论进行证明。
选取备选李雅普诺夫函数:
(18)
当θerr≠0,ω≠0时,因为ω0>0,Tω>0,得到2Tωω0θerrsign(θerr)>0。


(19)

当θerr=0,ω=0时,V=0。


(20)

3.2 沿直线行驶过程中的稳定性
移动平台在沿直线行驶状态下,|θerr|<ε,将式(12)、式(13)代入式(1),得
(21)
分析ρ和v的稳定性,得出如下结论:当|θerr|<ε时,在式(12)、式(13)的作用下,v在平衡点v3处是渐进稳定的,ρ在原点处是李雅普诺夫稳定的。下面对该结论进行证明。
先证明v在平衡点v3处渐进稳定。在该过程的初始时刻,有v(0)=0,根据式(21)可得到v(t)=v3-v3exp(-t/Tv)。因此,v是渐进稳定的,其平衡点为v3。当t>0时,v>0且最终收敛至v3。
下面证明ρ在原点处李雅普诺夫稳定。当t>0时,选择备选李雅普诺夫函数:
(22)
对式(22),当且仅当ρ=0时,V=0,否则,V>0。对V求导,并代入v(t)可得
(23)

上述证明过程说明,当|θerr|<ε且ε≪π/2时,状态θerr和ω并不影响ρ和v的稳定性。但是,状态θerr在原点是不稳定的。为便于分析,仅考虑ρ和v到达稳态的情况,此时,ρ=l,v=v3。在θerr=0及ω=0附近线性化,sinθerr≈θerr,从而可得
(24)
线性化系统的状态矩阵存在特征值v3/l,因此,当θerr≠0时,θerr将发散,直到θerr超过边界层,控制律使其重新收敛到ε内。θerr的发散速度取决于v3/l,选择较大的前视距离可减小θerr的发散速度,避免平台频繁调整姿态。
4 仿真分析
为验证上述控制算法的路径跟踪性能,以中煤科工集团重庆研究院的履带移动平台为原型,在Recurdyn中搭建动力学仿真模型,同时在Matlab/Simulink平台建立路径跟踪控制算法,通过Recurdyn和Matlab/Simulink联合仿真验证算法的有效性,分析前视距离对控制算法的影响,并与纯追踪算法进行对比。
4.1 不同前视距离下路径跟踪仿真
采用矩形路径作为平台的目标路径,设置ε=0.087 rad,初始平台位置在(0,0)附近,初始航向角为0,平台直线行驶速度为0.15 m/s,采样频率为10 Hz,前视距离l分别为0.4 m和0.8 m,仿真结果如图2所示。路径跟踪误差有多种定义方式,本文基于文献[17]中的方法,定义路径跟踪误差e为平台几何中心到目标路径的最短距离。
从图2(a)可看出,当前视距离为0.4 m和0.8 m时,算法对直线目标路径均具有较高的跟踪精度,但在转角处都出现了“抄近道”的现象。这是由于算法总是根据前视距离的大小预瞄目标路径点,根据当前位置和目标位置提前做出转向动作。从图2(b)可看出,因为初始点与目标路径相距较远,所以最大跟踪误差出现在初始点处,当平台开始运动后,误差逐渐减小。在稳态跟踪阶段,路径跟踪误差峰值出现在转角处,当前视距离为0.4 m时,转角处最大误差为0.180 9 m,前视距离0.8 m时,转角处最大误差为0.371 5 m。
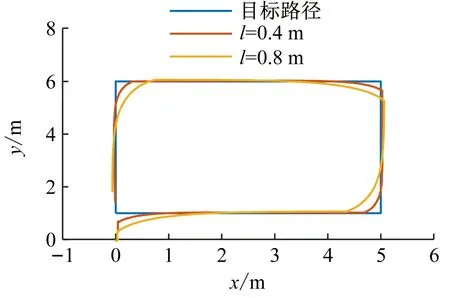
(a) 运动路径

(b) 跟踪误差
采用平均误差和稳态误差作为统计指标衡量路径跟踪质量[18],平均误差为整个跟踪过程路径跟踪误差的平均值,稳态误差为路径跟踪误差首次到达0之后路径跟踪误差平均值,统计结果见表1。从表1可看出,在保证稳定的前提下,选择较小的前视距离可提高路径跟踪精度。

表1 不同前视距离下路径跟踪仿真统计结果Table 1 Statistical results of path tracking simulation with different look-ahead distance m
4.2 对比仿真分析
设置纯追踪算法前视距离为0.4 m,且履带驱动轮可调速,其余条件与上文相同,对纯追踪算法和bang-bang控制算法进行对比仿真分析,结果如图3所示。
从图3可看出,直线跟踪阶段,纯追踪算法的跟踪误差略小于bang-bang控制算法;在整个跟踪过程中,纯追踪算法的平均跟踪误差为0.063 8 m,稳态跟踪误差为0.030 4 m,也略优于bang-bang控制算法;但在转角处,纯追踪算法出现了明显的超调,跟踪误差峰值为0.348 9 m,高于bang-bang控制算法。
对比2种算法的跟踪效率,纯追踪算法跟踪至最终目标点耗时约为208.8 s,bang-bang控制算法的耗时为284.8 s,纯追踪算法效率高于bang-bang控制算法,其主要原因在于带调速的纯追踪算法可以在速度为0.1 m/s的前提下持续跟踪目标点。
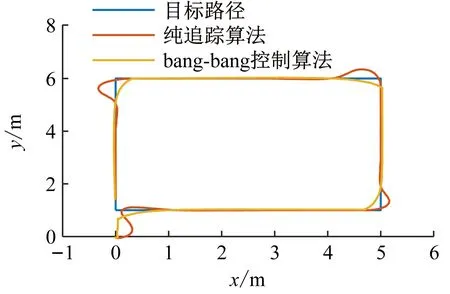
(a) 平台运动路径

(b) 跟踪误差
5 样机试验
5.1 试验样机
本文试验样机由中煤科工集团重庆研究院履带式移动平台进行改装得到,如图4所示。样机质量约为8 t,采用液压驱动的履带式摩擦底盘,履带间距为0.93 m,最大线速度约为0.15 m/s。移动平台电控箱上方安装有1个激光雷达和1个六轴惯性测量单元(Inertial Measurement Unit,IMU),用于同步定位与建图(Simultaneous Localization and Mapping,SLAM)。激光雷达型号为Velodyne VLP-16,测量距离为100 m,检测精度为±0.03 m。IMU型号为LPMS-BE1,其欧拉角测量分辨率小于0.1°,静态、动态测量精度小于2°。工控机用于SLAM和路径跟踪控制,PLC用于底盘电磁阀控制,工控机与PLC之间通过以太网Modbus协议通信。

自主导航行走系统架构如图5所示。

图5 自主导航行走系统架构Fig.5 Architecture of autonomous navigation system
5.2 路径跟踪试验
采用激光雷达及IMU建立测试场地的二维地图,然后基于地图坐标系规划目标路径。路径函数为y=-0.051 2x-0.143 5,起始目标点坐标为(2.4,-0.266 5)。履带移动平台以约0.05 m/s的速度跟踪目标路径,SLAM以10 Hz的频率实时输出激光雷达位置,通过坐标变换得到履带移动平台几何中心的位置。设控制算法前视距离l=0.5 m,ε=0.087 rad。进行2次试验,试验1中履带移动平台初始位置为(0.729 1,-0.262 7),试验2中履带移动平台初始位置为(1.520 7,-0.232 8),试验结果如图6所示。
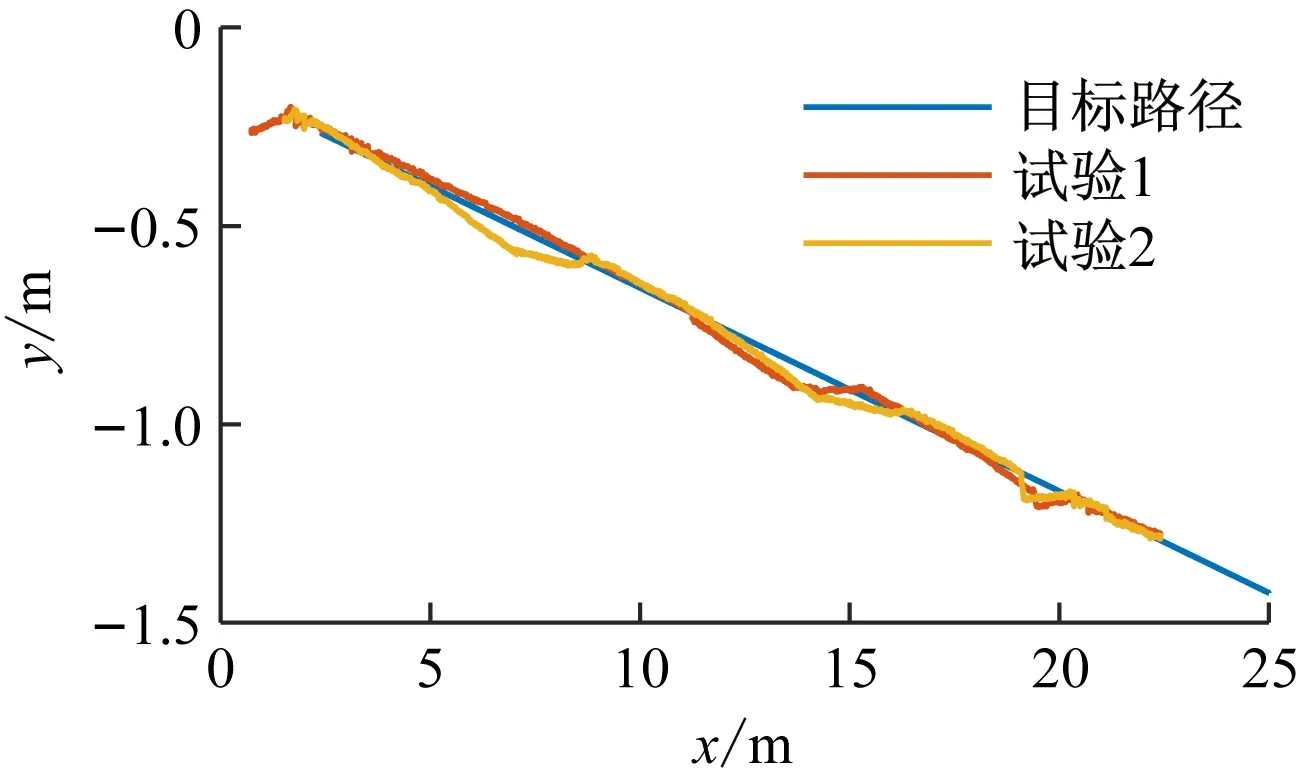
(a) 平台运动路径
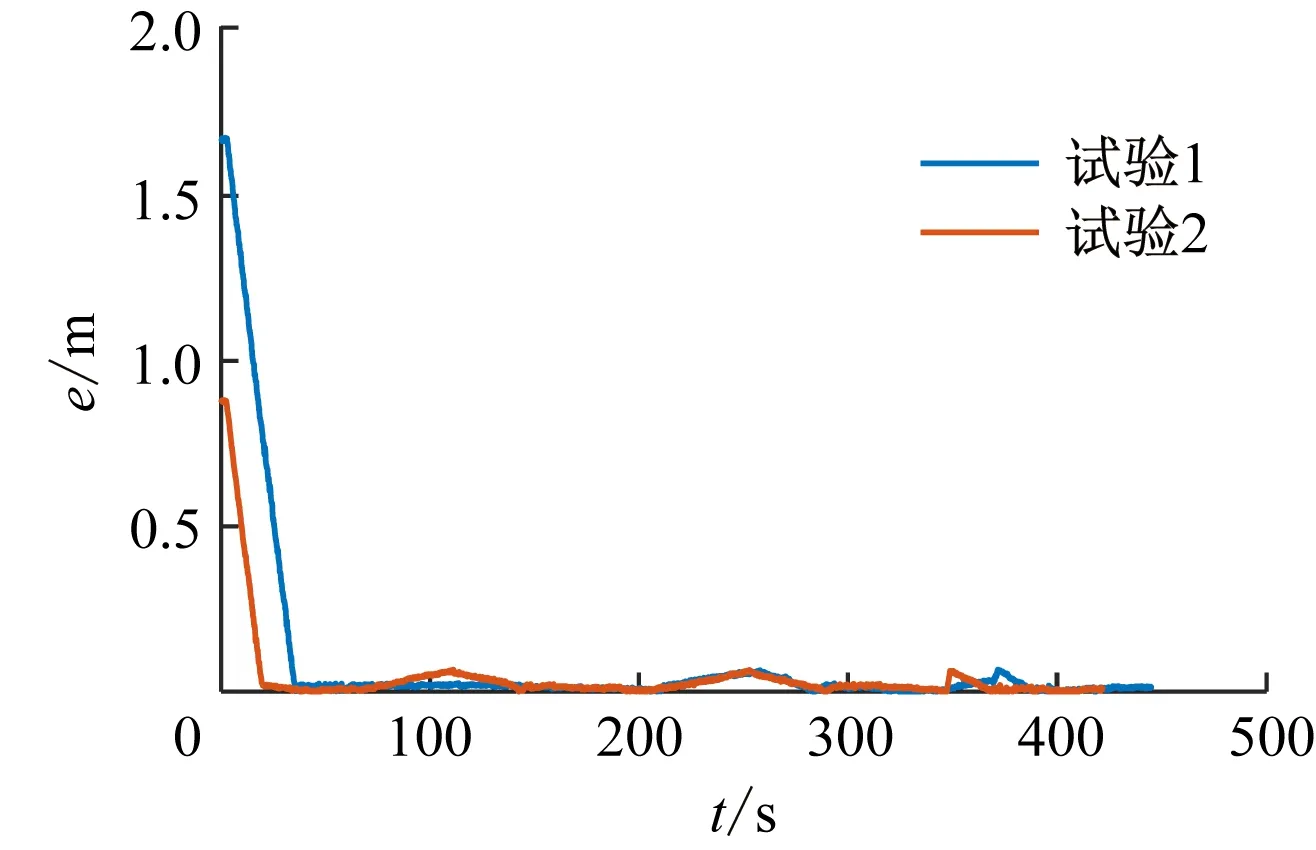
(b) 跟踪误差
从图6(a)可看出,履带移动平台启动后迅速向目标路径运动,在行驶过程中,当其偏离目标路径时,会调整前进方向,回到目标路径上。从图6(b)可看出,初始误差为履带移动平台与起始目标点的距离,当履带移动平台开始运动后,误差逐渐收敛至0附近。
2次试验的统计结果见表2。因为平均误差与初始位置有关,所以试验1的平均误差大于试验2;2次试验稳态误差均为0.02 m左右,说明系统路径跟踪稳态误差小且一致性较好。

表2 路径跟踪试验统计结果Table 2 Statistical results of path tracking experiments
6 结论
(1) bang-bang控制算法的平均跟踪误差及稳态跟踪误差略高于带闭环调速的纯追踪算法,但在转角处的跟踪误差小于纯追踪算法。
(2) 仿真分析和样机试验结果表明,bang-bang控制算法可用于无闭环调速履带移动平台的直线或折线类型路径跟踪,且稳态误差均小于9 cm。
(3) 在保证稳定的前提下,bang-bang控制算法可选择较小的前视距离,以获得更高的跟踪精度。
(4) 纯追踪算法仅包含前视距离1个调整参数,而bang-bang控制算法引入了边界层厚度,该参数对路径跟踪精度及跟踪效率有重要影响。边界层厚度越大,则跟踪精度越低,跟踪效率越高。下一步将对前视距离和边界层厚度的自适应调整进行研究。
