基于单位统计曲率特征匹配的红外目标检测方法
2021-06-02
(武汉理工大学 物流工程学院,武汉 430063)
0 引言
目标的自动检测是机器视觉中一项广泛应用的技术。例如,无人驾驶车辆的避障和道路安全的预警等。在过去的几十年中,目标检测技术得到了普遍的研究。然而,到目前为止,目标检测的各种方法对于复杂黑暗场景下的目标识别效果不佳。例如隧道施工现场,环境阴暗,浮尘和强光的存在,道路崎岖不平,导致包含检测目标的红外图像的信息存在很多干扰,现有的传统方法无法对目标进行可靠的检测。
现有的方法实现红外目标的检测在很大程度上取决于图像特征,例如边缘特征、不变特征和统计特征。基于边缘特征[1]的匹配方法首先提取目标的边缘信息,然后通过倒角距离匹配技术[2]来匹配目标的边缘,或者转换成其它特征,例如形状描述符[3]、轮廓描述符[4]或者感知驱动的图像特征[5],虽然采集的图像经过预处理,但在隧道环境中待识别的目标轮廓较模糊,依然不足以用这些方法准确识别。基于不变特征的方法主流是对照度和尺度特征的提取。SIFT、SURF和ORB都是基于局部不变特征的经典算法,有诸多学者针对此类算法进行了改进[6-8],然而,这些经典算法很难从一个红外图像的目标中提取足够多的关键点。Gray Histogram、Entroy、Unit Entroy、HoG和GIST等[9-12]统计特征方法,可用于表征红外图像中的目标,然而,Gray Histogram和Entroy仅仅依靠灰度值来检测目标,不包含任何关于像素位置的信息,这就会导致不同的目标可能被标识为相同的目标的问题。此外,当目标方向变化时,HoG和GIST不起作用。
实际隧道场景中机器人因自身的运动,获取的目标以及环境一直处于不断变化的状态下,针对此场景如果依旧使用传统的基于边缘、统计等特征的相关图像特征匹配算法就会存在一定的局限性。当视频中的目标方向和尺度发生变化,以及采集工具的视角、隧道环境中的照度等情况发生变化的情况下,传统算法无法进行可靠的识别,最终导致目标检测失败。为此,提出一种图像的单位统计曲率特征(unit statistical curvature feature,USCF),该特征比传统的特征具有更好的表征能力,不受隧道场景各种变化的影响。该方法实现过程为把由平均曲率和高斯曲率构成的曲率平面划分为多个单位,并对每个单位中的像素数进行计数,以构建USCF矩阵;USCF描述符使用图像中所有点的灰度值和位置信息,基于每个单位的平均曲率和高斯曲率分布的统计结果来表示待检目标的图像特征。
1 单位统计曲率特征匹配算法原理
为了检测红外图像中的目标,首先构建一个三维坐标系Οxyz如图1所示。其中(x,y,z)代表一个点,z是图像I中像素(x,y)的灰度值。
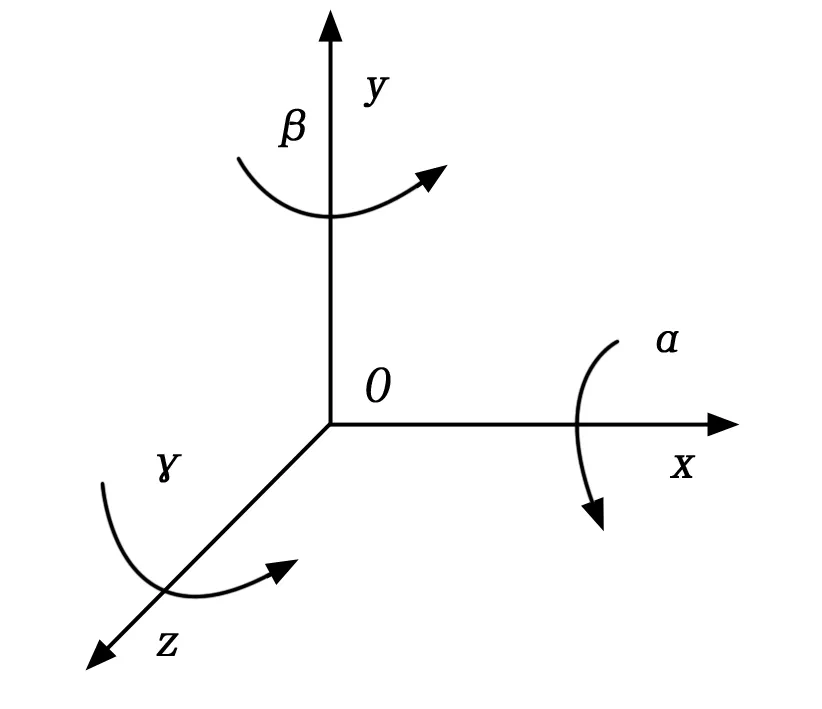
图1 三维坐标系示意图
构造如下表达式(1)的拟合函数以将Οxyz中的离散点转换为曲面,从而表示出图像I的灰度值分布趋势。
z=f(x,y)
(1)
图2展示了单个目标在不同条件下的拟合曲面,目标图像来自ALOI-COL数据库。第一列为原始目标,目标基本参数为尺度40×40像素(pixel,px),初始沿坐标系z轴方向旋转角γ为0°,初始照度为250勒克斯(lx),沿坐标系y轴方向旋转角β为0°,后边列依次只分别改变目标的γ角、照度、β角和目标尺度各一个条件,可以得到几个重要的结论。首先,初始目标的拟合曲面与其它条件变化的目标的拟合曲面不同,这意味着拟合曲面能用于唯一地表示一个特定目标;第二,如图2所示,在图像尺度和γ角,照度和β角变化的情况下,目标曲面的形状不变,因此,该方法非常适合隧道场景这种复杂环境下的目标检测;第三,曲面的形状随着目标缩放对目标的尺度不敏感,因此,如果能够提取物体的曲面形状的稳定特征,则可以有效地进行目标的识别。
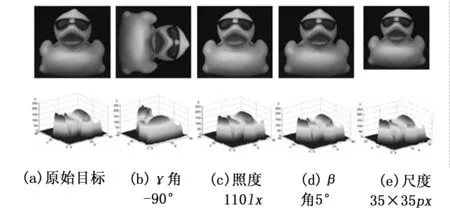
图2 目标在不同条件下的图像(上)和拟合曲面(下)
曲率不仅可以表示灰度值的分布趋势,并且能够描述曲面的局部形状。因此,本文采用曲率构造图像特征描述符来估计目标的相似度。目前主流大多采用梯度来表示图像的信息,在这种条件下,只需计算目标图像的一阶微分,此时目标的边缘能够突显,但目标的细节信息会保留较少。与梯度法相比,曲率法需要计算二阶微分,二阶微分对灰度值的变化非常敏感,可以更加突出目标图像的纹理结构,因此,曲率法包含更详细的目标图像的细节信息。此外,梯度法是相对于目标的γ角,当目标γ角变化时显示的图像特征不能保持不变,曲率法对于目标γ角变化和照度变化时显示的图像特征是不变的,因为它仅依赖于曲面的形状。
曲面的局部形状可以由两种曲率唯一而完整地表示:平均曲率和高斯曲率。平均曲率和高斯曲率在表示目标的特征时扮演着不同的角色,平均曲率反映曲面的局部形状特征,高斯曲率反映曲面的凹凸特征。因此,需要将高斯曲率K(x,y,z)与平均曲率H(x,y,z)结合起来以唯一地表示目标的特征描述符。
为了建立目标的特征描述,将K(x,y,z)和H(x,y,z)映射到二维坐标系OHK,如图3所示。使用(H,K)代表坐标系中的一个点,曲率平面可以反映灰度值分布的变化,倘若像素与其相邻像素之间的灰度值差异不大,则此像素的高斯曲率和平均曲率的绝对值都应该很小。因此,灰度值分布越平滑,越靠近坐标系原点的点越多;相反,当图像纹理发生显著变化时,与坐标系的原点相距越远的点越多。通常坐标系中的大多数点都靠近原点,因为平滑区域占图像的大部分。
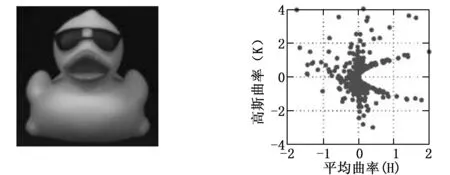
图3 目标的映射描述
每个像素的曲率是基于其邻域像素计算得出的,因此它对相邻像素的变化都很敏感;像素的灰度值的变化将影响曲率的值,这意味着目标的曲率平面对每个像素的灰度值的波动也很敏感。为了建立稳定的目标特征并有效地检测特征,将图3所示的目标的曲率平面划分为若干个单位区域,并对每个单位中的像素使用统计信息来生成稳定的曲率特征矩阵,即USCF。图4显示了目标在不同条件下的USCF矩阵,同样第一列为原始目标,目标基本参数同前文交代,这里不再赘述,可以看出不同目标的USCF矩阵显著不同,而相同目标在不同条件下具有相似的USCF矩阵。此外,目标尺度的变化只影响到每个单元中映射的曲率点的数量,不会改变曲率点分布的比重。结果表明,采用基于曲率和统计的方法,即使在不同的外部条件下,也能有效地识别出目标。
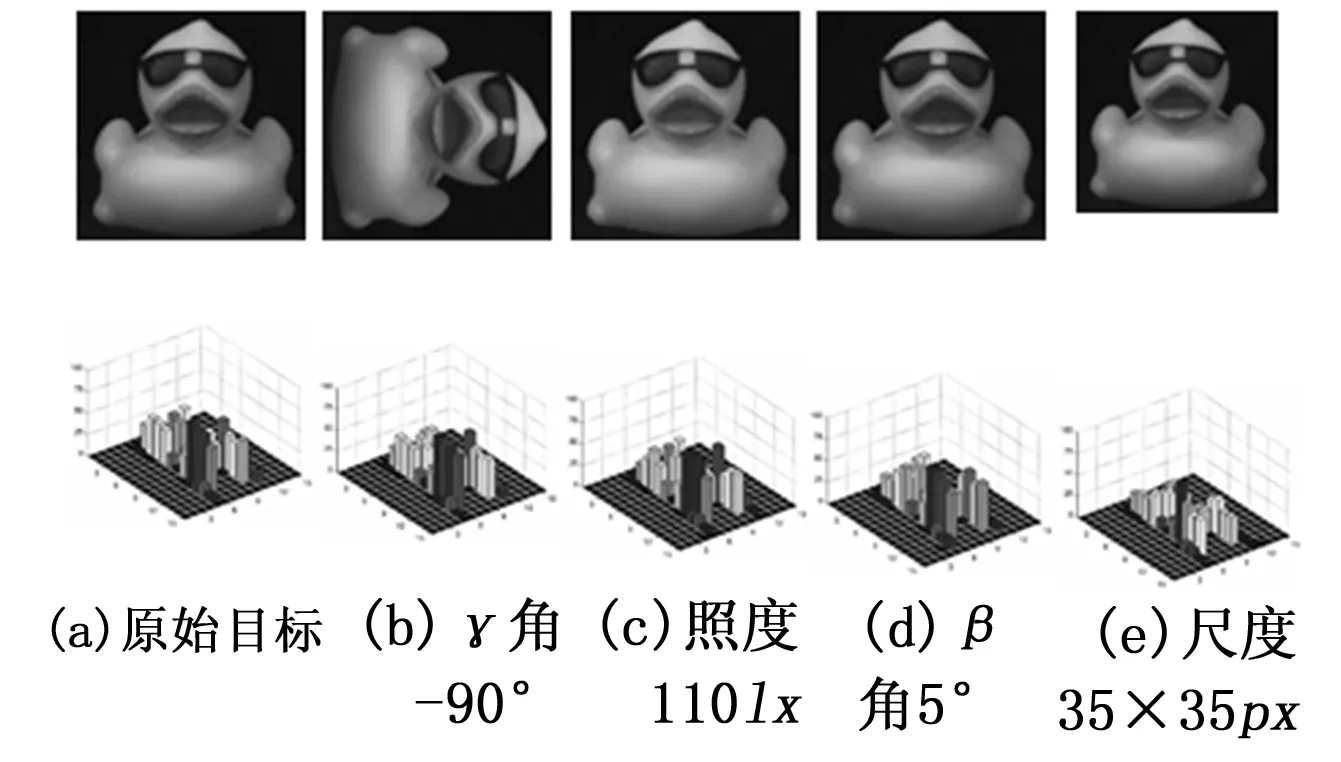
图4 目标在不同条件下的图像(上)和USCF矩阵(下)
USCF算法通过同时使用平均曲率和高斯曲率来检测目标,这两种曲率能精确地定义拟合曲面的局部形状。应用平均曲率和高斯曲率的不同形态的组合,能够得到8个基本的局部曲面形状,如表1所示。8个基本的局部曲面形状组合可以完全表示具有任意形状和纹理的图像目标,实际上,USCF矩阵就是这些局部曲面形状的统计结果。
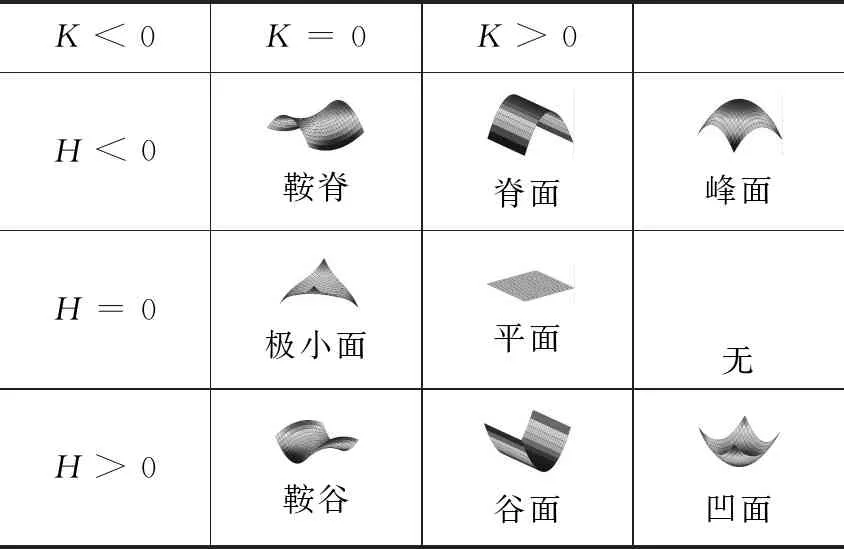
表1 局部曲面形状组合类型
目标γ角变化和照度的变化对拟合曲面的形状影响很小,而β角变化则会影响目标图像的纹理和拟合曲面的形状。此外,虽然在目标尺度变化时拟合曲面的基本形状可以保持不变,但图像细节纹理结构丢失,会影响USCF算法的检测精度。不过,轻微的β角变化和尺度变化对大多数纹理结构的相似性和USCF算法的检测精度影响不大,除非当目标尺度缩小很多时,图像的许多细节丢失,这可能导致拟合曲面的匹配失败。不过在这种情况下,对于不同尺度的目标而言,影响拟合曲面形状的主要关键点将保持相似;相比之下,由于缺少目标的关键点,SIFT、SURF和ORB等经典算法在目标检测中的检测准确率较低。
2 基于USCF匹配算法的实现过程
2.1 算法流程
首先,使用最小二乘法对目标图像的曲面进行拟合;其次,根据拟合曲面计算出目标图像中各像素的高斯曲率和平均曲率;第三步,建立曲率平面OHK,并根据曲率分布的密度将其划分为多个单位区域;然后,计算每个单位区域中的点数来构造USCF矩阵;最后,通过计算USCF矩阵之间的欧氏距离得到目标的相似性,从而达到检测目标的结果,流程如图5所示。
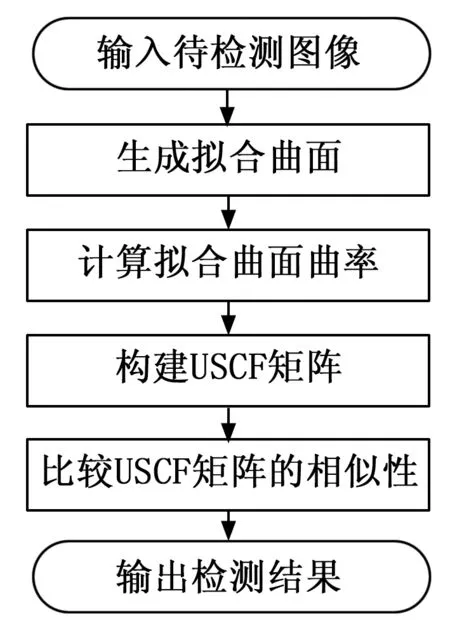
图5 USCF匹配算法流程图
2.2 具体步骤
定义x的P+1项的多项式函数为φr(x),其中r=0,1,…,P;定义y的Q+1项的多项式函数为φs(y),其中s=0,1,…,Q。
令φr(x)φs(y)为主函数,{crs}(r=0,1,…,P;s=0,1,…,Q)为未知系数的集合。可以构造一个函数来表示未知的曲面,如式(2)所示:
(2)
假设在坐标系中有(m+1)×(n+1)个点,点集表示为S={(xi,yj,zij)},其中i=0,1,…,m,j=0,1,…,n。由于曲面是拟合形成,因此拟合值与实际灰度值之间存在误差。定义实际灰度值和拟合值之间的平方差的总和,如式(3)所示:
(3)
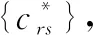
(4)
其中:r=0,1,…,P;s=0,1,…,Q。
拟合的曲面以矩阵形式表示如下式:
A=[φr(xi)](m+1)×(P+1)
B=[φs(yj)](n+1)×(Q+1)
Z=[zij](m+1)×(n+1)
(5)
将式(5)中的矩阵代入式(4),可以简化式(4)来获得系数值。最后,可以得到式(6):
C=(ATA)-1ATZB(BTB)-1
(6)
相应地,经过上述过程也就初步建立了点集S的拟合曲面f*(x,y)。
基于建立的拟合曲面,计算拟合曲面的曲率。拟合曲面的函数可以写为向量方程,如式(7)所示:
(7)
将f*替换为f*(x,y),可以得到关于向量t在x和y方向上的一阶微分和二阶微分,如式(8)所示:
(8)
通过定义曲面的基本形式,能够得到高斯曲率K和平均曲率H的值,如式(9)所示:
(9)
式中,E,F,G,L,M,N是曲面的第一基本形式和第二基本形式的参数,它们的值由式(8)的向量计算得出,如式(10)所示:
(10)
将式(9)中的参数替换为式(10)中的参数,并与式(8)结合,可以得到由f*的微分形式表示的高斯曲率K和平均曲率H,如式(11)所示:
(11)
通过式(11)可以根据图像的拟合函数得到目标图像中像素的高斯曲率K和平均曲率H。
获得坐标系OHK中的曲率平面后,就将其划分为w×v个单元,计算每个单元中的像素数,生成图像中目标的USCF矩阵。
由于坐标系中像素的分布不均匀,因此通过均匀划分曲率分布区域而获得的USCF矩阵是稀疏矩阵,无法唯一地表示图像中目标的细节。坐标系中的点分布广泛,但根据图3来看,大多数点都靠近原点。曲率平面的均匀划分将导致统计特征不均匀,例如,少数单元包含大多数点,而其它单元仅包含几个点,这将导致不同目标的USCF矩阵有很大的相似性。因此,需要根据图3中曲率坐标点的分布密度非均匀地划分曲率平面,以生成具有数量一致统计特征的USCF矩阵。图6给出了在像素大小相同的3个不同的目标的曲率平面的均匀划分和非均匀划分之间的比较,其中目标尺度均为40×40 px,其中图(b)为均匀划分的各目标分别对应的曲率平面,图(c)为非均匀划分的结果,可以看出,当均匀划分曲率平面时,大多数点散布在几个单元上,此时不同目标的USCF矩阵相似,这会严重影响检测目标的准确性;非均匀划分时将点平均分配给所有单元,可以提供足够的信息来比较不同目标的USCF矩阵,从而达到目标检测的目的。

图6 不同目标曲率平面均匀分区和非均匀分区的比较
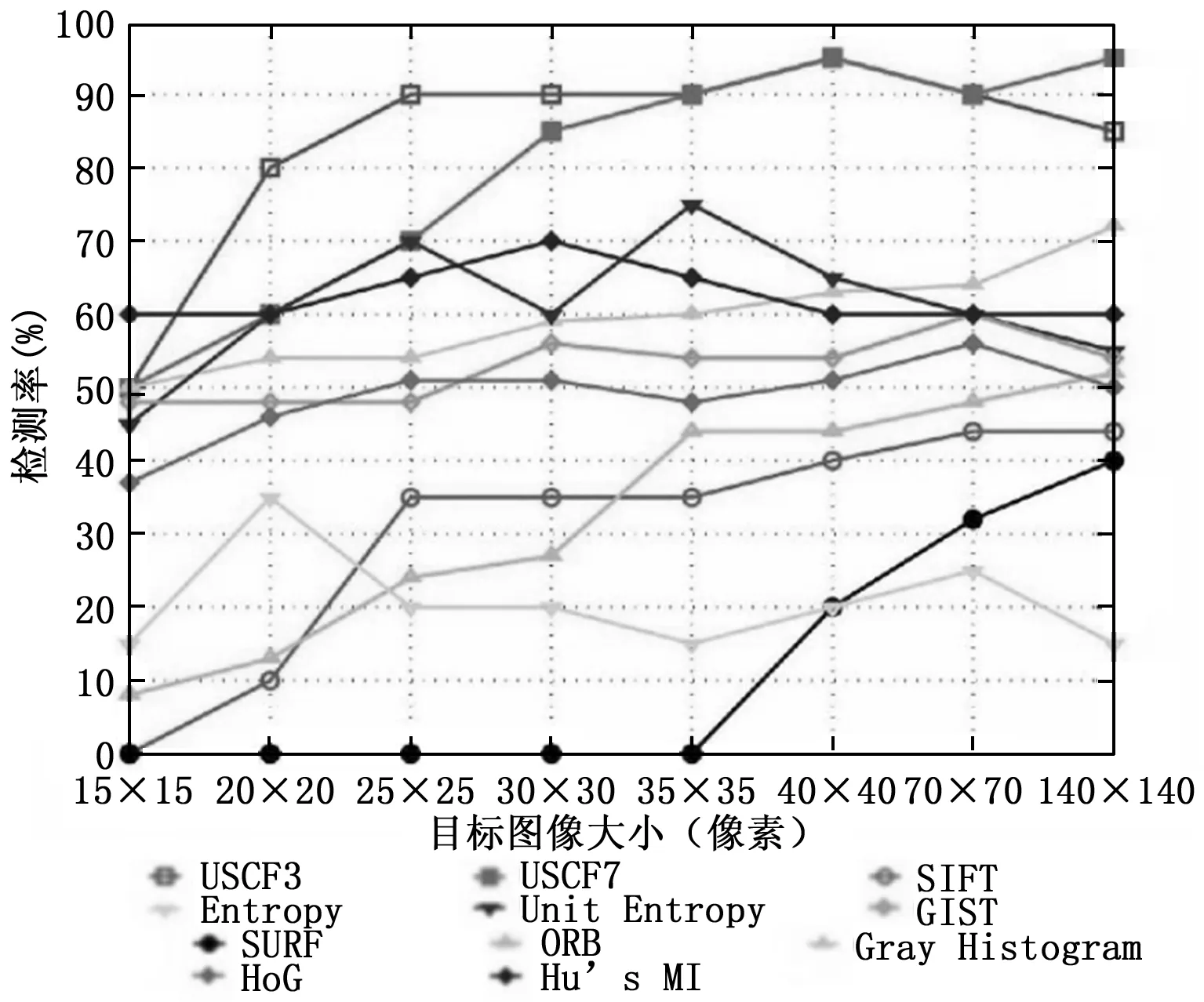
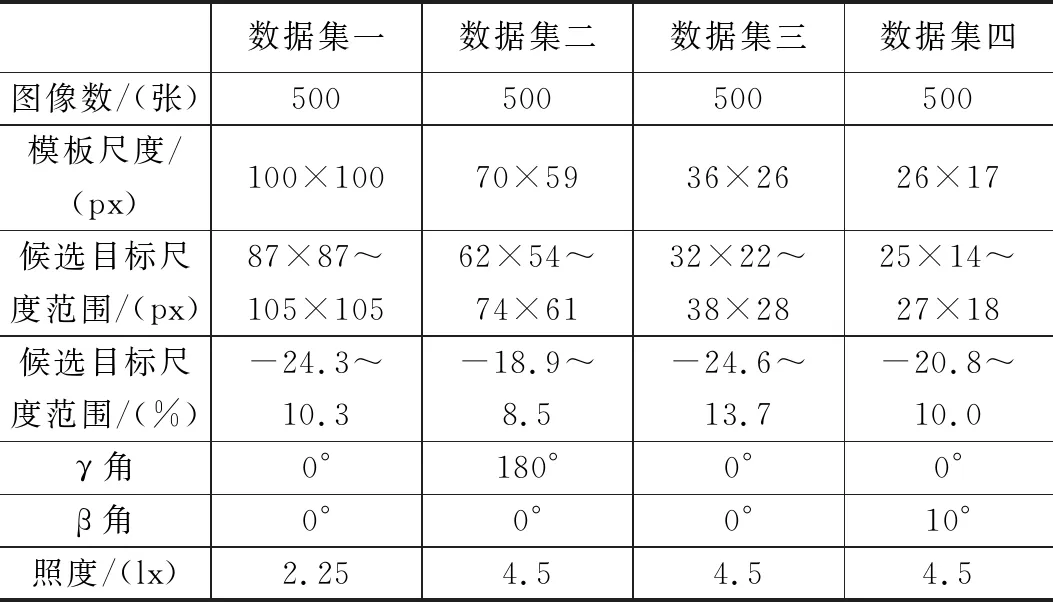
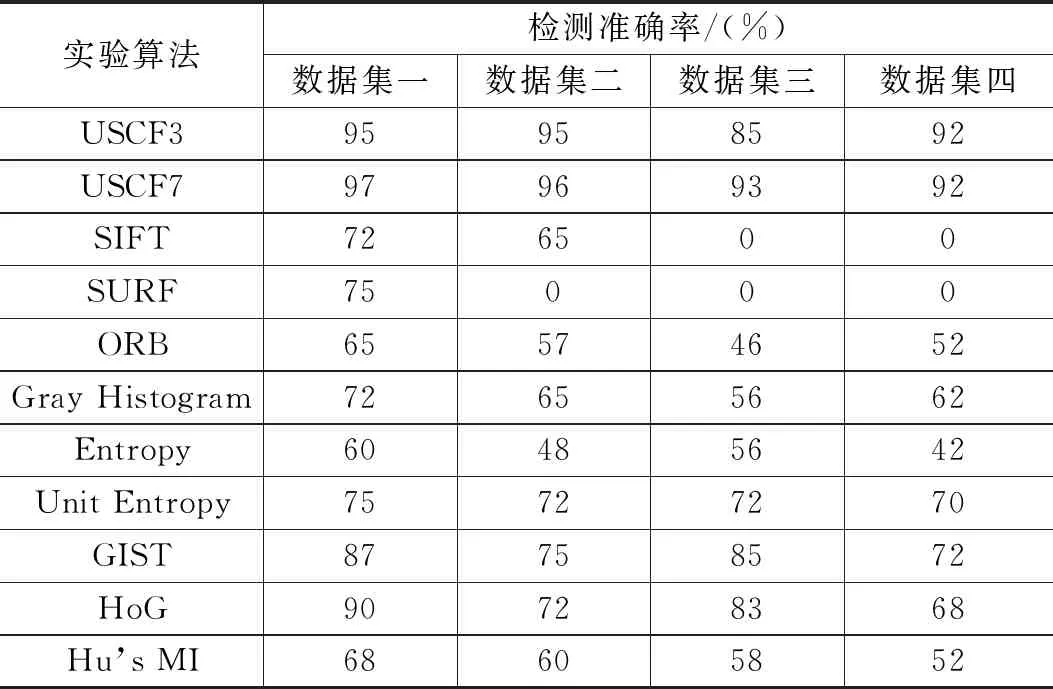
假设定义一个目标的曲率平面为Area,其表达式为Area={(H,K)|a Areaji={(H,K)|Hi-1 (12) 其中:i=0,1,…,w,j=0,1,…,v。 使用count(Areaji)表示曲率坐标(H,K)位于Areaji中的像素数。随后,可将USCF矩阵定义如下: D=[count(Areaji)]v×w (13) USCF矩阵D反映目标曲面的曲率特征,可以使用矩阵D表示曲面拟合的图像。USCF算法的检测精度在很大程度上取决于曲率平面的划分方式,曲率平面划分的单元越多,保留的图像目标纹理的细节就越多。同时,由于单元分区面积较小,削弱了目标的总体特征并且对局部特征的变化更加敏感,因此检测的结果容易受到图像变化的影响;另一方面,曲率平面被划分的部分数量越少,USCF算法对于图像变化的抗扰性就越好,但会降低算法的检测精度。因此,选择合适的分区划分来构建矩阵对于成功检测的结果尤为重要。 通过计算模板目标图像和候选目标图像的USCF矩阵之间的欧氏距离,判断检测目标的相似性。定义D[i,j]表示位于矩阵D的第i行和第j列的元素,定义DT和DM分别代表模板目标图像和候选目标图像的USCF矩阵,定义dist为测量DT和DM之间相似度的度量的欧氏距离。通过对结果的归一化处理,将矩阵中的每个元素除以矩阵中所有元素的总和,使所有值都在区间[0,1]之间。应用式(14)来计算模板图像与候选图像之间的相似度,如果DT=DM,则结果为零。 (14) 本文搭建隧道机器人作为实验平台,如图7所示。机器人用于采集视频和图像的红外摄像头固定在机器人正前部,通过USB串口与机器人内仓的工控机进行通信。机器人基座为履带式差速驱动的移动平台,通过内置搭载工控机运行程序,实现移动机器人进行栈桥的检测。本文使用ETH-80数据集,ETHZ数据集和Ukbench数据集中的图像作为示例目标,程序在Windows平台下编写,程序开发环境为Visual Studio 2013,使用计算机视觉库OpenCV 3.4.1实现栈桥的检测,并分别改变目标的尺度、γ角、照度、β角多个条件将USCF算法与SIFT,SURF,ORB,Gray Histogram,Entroy,Unit Entroy,GIST,HoG和Hu’s MI九种算法进行对比实验,通过数据集的样本和隧道实际场景中的栈桥对该算法的检测准确率进行评价。 图7 机器人实验平台 曲面拟合参数的选择会影响USCF算法的结果。当计算一个像素的曲率时,用于拟合一个局部曲面的像素周围的像素越多,得到的曲率值越准确。现分别在3×3(标记为USCF3)和7×7(标记为USCF7)领域像素中拟合了一个局部曲面,这样做是为了比较不同大小的窗口的效果。 对于USCF3,由于拟合曲面的形状较简单,可以用低阶多项式表示主函数。定义曲面逼近函数f3(x,y)如下: (15) 对于USCF7,拟合曲面的形状比USCF3复杂,因此使用更高阶的多项式表示主函数。定义曲面逼近函数f7(x,y)如下: (16) 经过实验后,得出大多数像素的平均曲率H和高斯曲率K分布在(-1 000,1 000)的范围内,根据经验将分布区域分别划分为11个部分和17个部分,每个部分都包含足够的点以区分目标并消除干扰。使用此分区,能够取得较好的检测精度。分界点表达式如下给出: (17) 其中:i=0,1,…,11,j=0,1,…,17。 在实验中采用最近邻近似匹配策略,对SIFT,SURF和ORB算法中的候选目标和模板目标进行至少3个关键点的匹配;对于Entroy算法,模板和候选目标图像之间的熵差的绝对值作为匹配准则;对于Unit Entroy和HoG算法,每个单位的尺度设置为5×5 px;直接应用Hu’s MI算法对整个图像进行匹配,使用特征向量的余弦值作为衡量模板目标和候选目标图像相似性的指标;对于Gray Histogram和GIST算法,使用欧式距离比较它们特征向量的相似性。 在隧道环境中,目标检测通常是在复杂的条件下进行的,其中多个变量(包括目标尺度及γ角,光照和β角)同时变化,而不是单个变化。本文首先利用ETH-80和ETHZ数据集的53个目标对算法在复杂条件下的检测性能进行测试,参照隧道机器人的行驶速度和采集的栈桥样本,设定实验中使用的目标尺度分别为15×15、20×20、25×25、30×30、35×35、40×40、70×70和140×140 px。在这两个数据集中,每个目标都处于不同状态(例如上下颠倒,β角不定,尺度不一,照度变化),部分测试图像如图8所示。 图8 测试目标图像示例 图9给出了实验后不同算法的检测性能统计,可以看出,当目标的尺度在25×25至70×70 px范围内时,USCF3的检测准确率超过90%,当目标尺度为40×40 px时,USCF3算法的检测准确率达到最佳的95%;当目标的尺度从35×35到140×140 px时,USCF7的检测准确率也超过90%。当拟合局部曲面时,靠近目标图像边界的点没有足够的邻域像素来拟合,因此无法计算这些点的曲率。窗口大小越大,丢失的像素信息就越多,USCF7比USCF3丢失更多的像素信息,当图像尺度小于40×40 px时,USCF7丢失了超过30%的像素信息,远超过了USCF3的5%。当目标尺度增加时,由于靠近边界的点在整个图像中所占的比例减少,窗口大小的影响也随之减小。因此,对于采集的距离更远的目标,USCF3的性能优于USCF7,对于距离较近的目标,USCF3的表现较USCF7差,但总体而言,USCF算法的检测性能优于其它的9种算法。 图9 不同算法在复杂环境条件下的实验结果 如图9所示,在该实验中,USCF算法具备最佳的检测性能。由于Unit Entroy、HoG和GIST算法对目标的γ角变化较敏感,因此,Unit Entroy算法的最佳性能仅为当目标尺度为35×35 px时的75%,而HoG和GIST算法对所有尺度目标的检测准确率均不超过60%;随着目标尺度从15×15 px增加到140×140 px,Gray Histogram的检测准确率从50%增加到72%,这是因为Gray Histogram算法基于灰度值(颜色)分布,目标之间的颜色分布差异很大,并且随着目标尺度的增大而变得更大;Hu’s MI算法的最佳检测准确率为当目标尺度为30×30 px时的70%;当目标尺度为20×20 px时,Entroy算法的检测准确率达到最佳仅为35%;在这种复杂的条件下,ORB、SIFT和SURF算法的性能相对更差,当目标尺度为140×140 px时,SIFT和ORB达到最佳检测性能,检测准确率分别为44%和52%,而当目标尺度小于35×35 px时,SURF算法无法执行有效的检测,由于本实验中的样本选择均参考隧道内的目标和环境的情况,因此使用的很多目标只有一个或多个不同界面的颜色块,应用ORB、SIFT和SURF算法,很难从这些色块中提取关键点,即使在目标很大的情况下,这3种算法在本实验中的效果也不理想。 为了进一步检验USCF算法在复杂环境条件下的性能,在下面的实验中使用了目标尺度为64×48 px的Ukbench数据集。与前文实验的数据集相比,Ukbench数据集的目标包含更复杂的特征,例如精细的纹理,模糊的颜色边界和更多的背景干扰,从Ukbench数据集中选择的部分测试图像如图10所示。 图10 Ukbench数据集中的测试目标图像示例 对于来自Ukbench数据集的测试图像的实验结果如表2所示,USCF3在实验中的测试算法中性能最佳,检测准确率为93.6%,USCF7的表现比USCF3差,检测准确率为74%,这是因为USCF7使用了更多的相邻像素来拟合局部曲面,与USCF3相比,该算法具有更高的曲率精度,但更容易受到目标图像变化的影响。在复杂的环境中,Hu’s MI、Gray Histogram和Entroy算法几乎无法进行有效检测,检测准确率不超过23.2%;Unit Entroy、HoG和GIST算法的检测准确率不超过80%,Unit Entroy的检测准确率仅为56.8%;ORB,SIFT和SURF算法的性能也很差,在3种算法中ORB的性能最佳,但其检测准确率最佳也仅能达为61.6%。实验结果表明,USCF可用于检测复杂条件下的目标,如现实隧道环境中的目标检测。 表2 使用Ukbench数据集测试图像的实验结果 为了评估USCF算法在隧道环境中的检测性能,本部分对红外摄像头采集的视频中截取的液压栈桥图像进行了在背景干扰、栈桥尺度和γ角变化、β角变化和照度变化条件下的检测实验。测试图像上的信息分为4个图像数据集,目标的尺度从数据集一到数据集四逐渐减小,数据集一、二、四和其它数据集相比,分别改变各自的照度、γ角和β角,具体参数如表3所示。图11给出了数据集中的目标模板的样本示例及使用USCF算法的检测结果。所有的测试图像都是直接从视频中剪辑出来,从一帧图像中分割出目标的图像作为模板,并使用其他帧中具有相似比例的图像作为候选图像。 表3 实验中使用的测试图像数据集信息 图11 部分模板图像和检测结果示例 本文对上述4个数据集使用其它9种算法进行检测实验,最终检测准确率统计如表4所示。在测试算法中,USCF3和USCF7的检测性能最好,检测准确率在85%~95%和92% ~ 97%之间;而在其它算法中表现最好的HoG和GIST的检测准确率在68% ~ 90%和72% ~ 87%之间,在数据集四中,当栈桥β角发生轻微变化,HoG和GIST的表现较差,二者的检测准确率分别仅为68%和72%;在图像数据集一中的实验结果表明,基于灰度值的统计算法(如SIFT,ORB,Gray Histogram,Entropy,Unit Entropy和Hu’s MI)受到目标照度变化的影响较大,当图像照度发生明显变化时,此类算法的检测准确率均低于80%;SURF无法检测图像中过小的目标,因此在数据集二、数据集三和数据集四中不起作用。 表4 实验算法对栈桥数据集的检测性能比较 实验结果表明,USCF算法根据曲率平面上的曲率分布对单元进行非均匀分割,而在原始图像上不进行均匀分割,在目标环境和条件发生变化时具有较强的鲁棒性。从4个数据集的实验中能够看出,无论是目标尺度和γ角的改变,还是β角和环境的照度发生变化,USCF3和USCF7的检测准确率均超过85%,该算法在实际工程中栈桥检测的表现出色。 传统特征匹配的目标检测方法在隧道机器人的实际应用中,受检测目标尺度、β角和γ角变化,环境中照度变化和背景干扰的影响,导致检测准确率较低的问题。本文提出了一种基于单位统计曲率特征(USCF)匹配算法,首先介绍了该算法的原理及实现过程,该算法通过计算目标图像的灰度拟合曲面中每个像素的平均曲率和高斯曲率,生成单位统计曲率特征矩阵来表征目标,保证提取更稳定的目标图像特征;然后通过调整变量的方法对于图像数据集进行多组对比实验,检验该算法在实际环境中的可行性;最后,依照在实际隧道的复杂环境下进行液压栈桥检测实验,USCF算法的检测准确率在所有测试算法中最高,结果表明,USCF算法对目标尺度、γ角和照度的变化具有较强的鲁棒性,并且可以容忍轻微的β角变化。本文算法对于隧道工程中机器人的目标检测具有良好适应性,能够提高机器人在隧道施工场景中目标检测的检测准确率。3 USCF匹配算法对比实验与评价

3.1 实验参数的选择
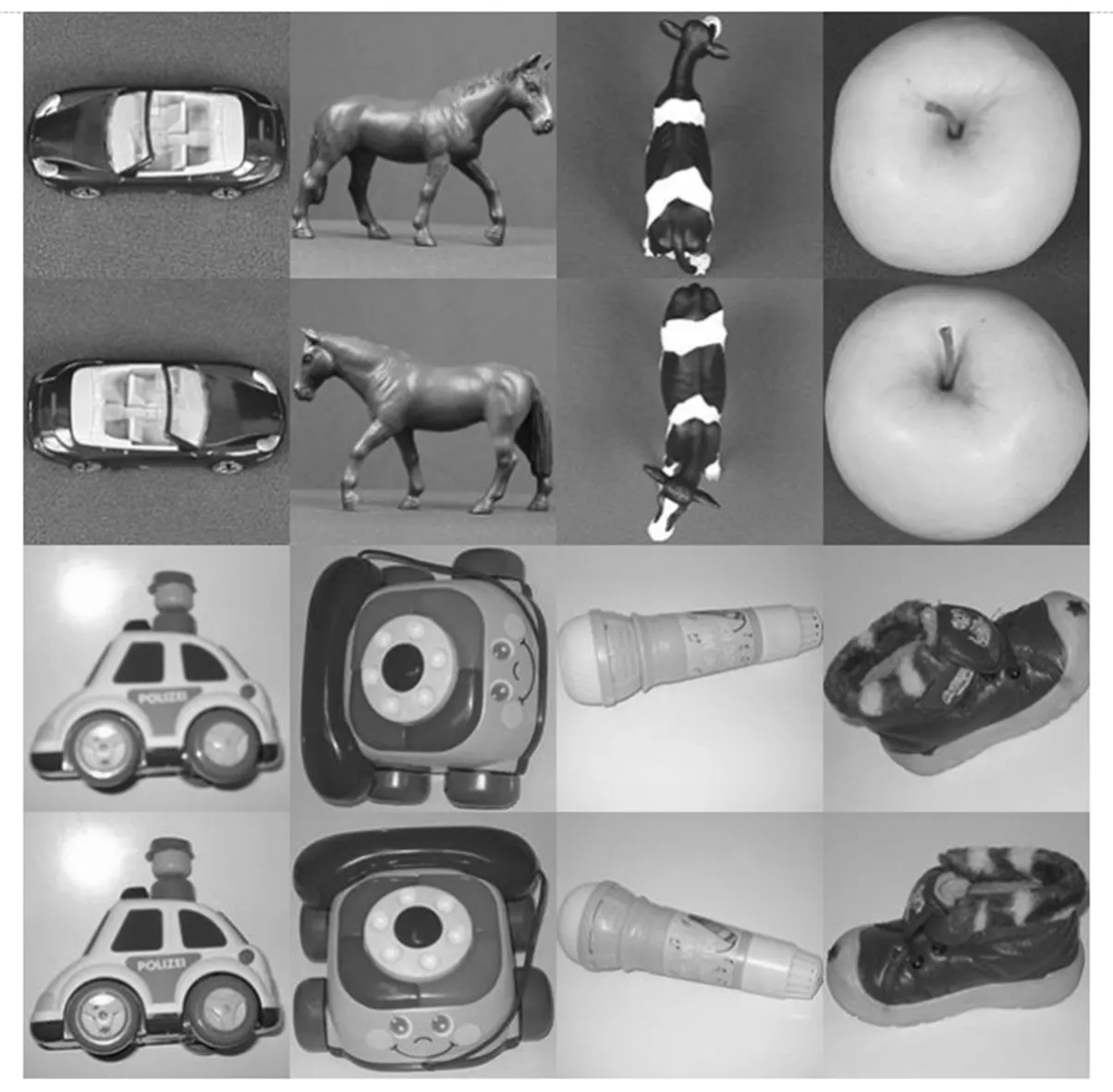
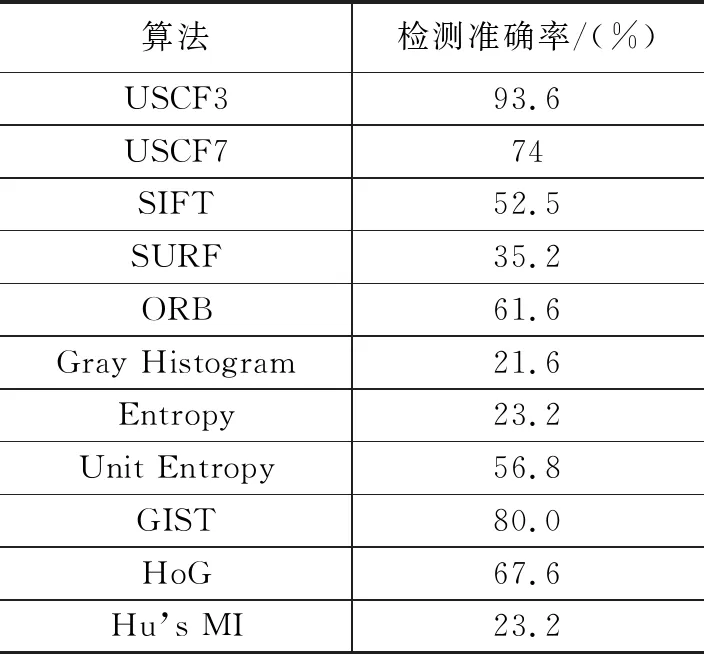
3.2 数据集目标的检测实验与分析

3.3 栈桥检测实验与分析

4 结束语
