丘陵小流域氮磷流失通量监测频次的优化研究*

蔡燕秋 唐翔宇 张建强 程 军 唐家良 章熙峰

(1.西南交通大学地球科学与环境工程学院，四川 成都 611756；2.中国科学院、水利部成都山地灾害与环境研究所，四川 成都 610041)

河流是流域内污染物迁移进入湖泊、水库等水体的主要途径。河流的水质指标和径流量是污染物流失通量计算的重要依据。由于高频次水质监测的成本较高，我国各地区水质监测频率一般为1～4次/月，在污染物流失通量计算时需要通过线性插值法或非线性插值法进行估算。在人类活动强度高的区域内，水质与水文情况复杂，线性插值法严重偏离实际情况[1]。已有多种模型如SWAT、雨水管理模型(SWMM)等[2-6]被应用于较大流域污染物流失通量的估算，但此类模型并不适用于小流域。

河流污染物流失通量与径流量间一般存在着较好的相关关系，美国地质调查局(USGS)据此开发了LOADEST模型。该模型能利用连续的径流量数据和离散的水质数据，建立污染物流失通量与径流量之间的非线性回归方程，因其符合污染物波动式流失的常态，并且操作简便、数据需求量小，已被广泛应用[7-10]。宋方方[11]通过LOADEST模型对赵家溪污染物流失通量进行估算，为赵家溪污染控制方案的制定提供数据支撑；DWIVEDI等[12]研究发现，LOADEST模型用于估算低水平范围的大肠杆菌负荷有较好的效果；JHA等[13]用LOADEST模型对美国纽斯河的氮磷流失通量进行估算，发现估算值与实测值相比总体偏高；PARK等[14]指出回归方程不仅与水质参数有关，而且与暴雨事件样本所占比例有关；高信娟[15]在九龙江的研究结果表明，水质数据缺失越少，污染物流失通量的估算值越接近实测值。

本研究以四川省盐亭县万安丘陵小流域截流、大兴及万安3个河流断面为对象，比较不同监测时间间隔条件下总氮(TN)、总磷(TP)日流失通量估算值相比实测值的相对误差，以确定既经济可行又结果可靠的最低监测频次，并揭示小流域属性的空间尺度差异所产生的影响。

1 材料与方法

1.1 研究区

研究区位于四川省盐亭县万安小流域(105°27′E，31°16′N)，海拔为389～426 m，属中亚热带季风气候。2015年、2016年和2017年的年降雨量分别为1 029.3、886.7、628.7 mm，其中5—10月降雨量占全年总降雨量的比例分别为87%、83%和76%。该小流域内截流、大兴、万安集水面积分别为0.35、4.80、12.36 km2。研究区概况见图1。

图1 万安小流域概貌与监测点位置Fig.1 Map of Wan’an catchment and monitoring locations

1.2 LOADEST模型

LOADEST模型参数的估计方法有极大似然估计(MLE)法、校正极大似然估计(AMLE)法和最小绝对偏差(LAD)法3种。一般采用AMLE法，但当残差不符合正态假设时，则考虑采用LAD法。当源文件中将模型选择设置为0时，LOADEST模型运用Akaike信息准则(AIC)[16-18]和Schwarz后验概率准则(SPPC)[19]，自动从9个回归方程(见式(1)至式(9))中取得最小AIC值和SPPC值的方程为最优方程，并进行自变量中心化消除多重共线性[20]。

lnL=a0+a1lnQ

(1)

lnL=a0+a1lnQ+a2lnQ2

(2)

lnL=a0+a1lnQ+a2td

(3)

lnL=a0+a1lnQ+a2sin(2πtd)+a3cos(2πtd)

(4)

lnL=a0+a1lnQ+a2lnQ2+a3td

(5)

lnL=a0+a1lnQ+a2lnQ2+a3sin(2πtd)+
a4cos(2πtd)

(6)

lnL=a0+a1lnQ+a2sin(2πtd)+a3cos(2πtd)+a4td

(7)

lnL=a0+a1lnQ+a2lnQ2+a3sin(2πtd)+
a4cos(2πtd)+a5td

(8)

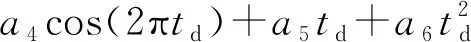
(9)

式中：L为污染物流失通量；a0～a6为回归系数；Q为径流量；td为分数化的时间与中心化时间之差；参数单位均视具体情况而定。

LOADEST模型主要通过以下3种方式检验回归方程的有效性：(1)判定系数(R2)越接近1，证明方程的拟合程度越好；(2)残差序列相关系数(SCR)越接近0，证明方程的各残差之间越独立；(3)概率曲线相关系数(PPCC)越趋近于1，表明残差越接近正态分布。

1.3 方法比较与优化

于2015—2017年，在上述3个河流断面进行径流量的连续监测，并对河水TN和TP两种污染物指标开展采样监测，频次为雨季(5—10月)每周1次、非雨季(11月至次年4月)每10天1次。

采用LOADEST模型以不同时间间隔条件下的水质数据和连续的径流量数据(日数据)分别对3个河流断面的TN和TP日流失通量进行估算。为避免监测日期选择的偶然性，将用于流失通量估算的污染物浓度数据起算日期错开得到时间间隔相同的不同数据分组。采用式(10)计算2015—2016年较大与较小时间间隔条件下污染物总流失量估算值的相对误差：

(10)

式中：RE为相对误差，%；Li和L10为用LOADEST模型估算得到的时间间隔为i及10 d时某断面的污染物两年总流失量，kg；i为时间间隔，d。

2 结果与讨论

2.1 污染物流失通量的时空变化特征

由图2可见，在时间分布特征上，雨季各断面的TN、TP日流失通量的平均值明显高于非雨季，且在雨季的波动范围比非雨季大。从空间尺度来看，截流断面的TN、TP日流失通量的平均值明显低于大兴和万安断面；大兴断面的TN日流失通量略高于万安断面，其TP流失通量平均值与万安断面在非雨季基本持平，而在雨季略高于万安断面；截流断面在雨季与非雨季的TN、TP日流失通量波动最大，动态变化特征最为突出。

2.2 回归方程的有效性

表1给出了不同监测频次下3个河流断面的TN和TP流失通量回归方程的R2。对于水质监测时间间隔相同的不同数据分组应选择不同的最优回归方程。可以看出，大部分方程的拟合程度均比较好，除大兴断面外，R2在0.75以上。SCR为0.01～0.57，表明部分模型拟合受到共线性影响，且受影响的模型为水质监测时间间隔为30～40 d的数据分组。PPCC均在0.9以上，表明各污染物流失通量回归方程的参数估计均可采用AMLE法。

表1 截流、大兴及万安断面污染物流失通量回归方程的检验结果1)

2.3 不同监测频次污染物总流失量估算值的相对误差分析

为验证水质监测时间间隔为10 d条件下小流域污染物流失通量LOADEST模型估算值的可靠性，将其与流失通量实测值(污染物浓度实测值与日径流量实测值的乘积)的时间变化特征对比，结果表明：污染物日流失通量的估算值与实测值吻合较好(估算值相对误差在-25%～25%的数据占49.59%)，动态变化特征基本一致(见图3)。因此，可采用水质监测时间间隔为10 d的污染物流失通量估算值作为参比值，验证较大的监测时间间隔条件下污染物流失通量估算值的相对误差。

图3 监测时间间隔为10 d条件下污染物流失通量LOADEST模型估算值与实测值的时间动态变化Fig.3 Dynamics of the estimated pollutant loss flux in the river using LOADEST with the measured pollutant loss flux at a time interval of 10 d

较大的监测时间间隔条件下污染物两年总流失量估算值(大兴断面部分数据由于无法收敛而缺乏参数估算结果)的相对误差见图4。结果表明，对于同一个河流断面，在校准文件中输入不同时间间隔条件下的污染物浓度及日径流量实测数据时，所得到的污染物总流失量估算值存在差异。相对误差绝对值最小为0.07%，最大为148.08%，说明不同时间间隔条件下获得的两年总流失量估算值之间存在极大差异。从相同时间间隔的不同数据分组来看，在40 d间隔条件下，截流断面TN总流失量估算值的相对误差变化范围很大，但万安断面TN总流失量估算值却较为稳定。尽管截流断面在不同监测时间间隔条件下获得的TN流失通量最优回归方程R2均在0.94以上，但其两年总流失量的模型估算值之间却存在较大差异，这表明影响截流断面TN流失的相关因素及过程随时间推移呈现随机、非单调性变化。

图4 不同监测时间间隔条件下两年总流失量的LOADEST模型估算结果及相对误差Fig.4 The estimated 2-year total exports of pollutants based on monitoring data obtained at different time intervals and their relative errors

从不同的监测频次来看，时间间隔为20 d条件下，不同河流断面的污染物总流失量估算值的平均相对误差为10.70%；时间间隔为30 d条件下，平均相对误差为15.02%；时间间隔为40 d条件下，平均相对误差为31.76%。这说明水质监测时间间隔越长，污染物总流失量的估算值与实测值的偏差可能越大。

注：STN、STP分别为单位集水面积TN、TP日流失通量，g/(d·hm2)。图2 2015—2016年河流断面的非雨季与雨季单位集水面积实测污染物日流失通量Fig.2 Daily pollutant loss flux per unit drainage area in non-rainy and rainy season during 2015-2016

从不同污染物来看，TN的平均相对误差为28.93%，TP的平均相对误差为20.90%。这说明LOADEST模型对TP流失通量的估算更为可靠，但对TN流失通量估算的适用性相对较差，此结果与KIM等[21]得出的结果相似。

以25%作为污染物总流失量LOADEST模型估算的允许误差，由表2可以看出，截流断面TN和TP流失通量监测最大时间间隔为20 d；大兴断面TN监测最大时间间隔可设定为30 d，而TP流失通量则不能用LOADEST模型估算；万安断面TN和TP监测最大时间间隔为40 d。

表2 各河流断面模型估算结果在25%允许误差范围内的占比

丘陵小流域水文过程一般存在显著的空间尺度变化规律，溪沟河流的径流系数随集水面积增加先增大而后趋于恒定，降雨径流量和污染物流失通量随时间的变化也逐渐趋于平缓。本研究的数据表明，当集水面积过小，污染物流失通量的估算值相对于实测值的误差不稳定，因此需要加大监测频率才能增加模型输出结果的可靠性。

2.4 模型外推可行性分析

利用2015—2016年污染物浓度数据与2015—2017年径流量数据外推得出2017年氮磷流失通量，与用2017年水质指标和径流量实测数据计算出的结果相比较，验证外推的可行性。由表3可以看出，外推估算值与实测值差异较大，相对误差最高可达182.70%。因此，外推估算法不可行，对于该丘陵小流域，当年径流量与水质实测数据都是准确估算当年TN、TP总流失量的必要数据，气象水文情况的年际变化会对估算结果产生不可忽视的影响。

表3 污染物年总流失量的LOADEST模型外推估算值和实测值

2.5 模型估算误差的来源分析

2015—2016年各河流断面污染物浓度的变异系数分析表明，大兴断面TN、TP浓度的变异系数均为最高，截流断面次之，万安断面的变异系数最小(见表4)。浓度分布越离散，就需要越多的数据才能实现模型的良好拟合。因此，在相同监测频次下LOADEST模型在大兴断面表现较差，而在万安断面则表现良好。

表4 河流各断面污染物浓度的变异程度及集水区基本属性

结合集水区的基本属性，可辨识污染物浓度的变异原因。一般而言：集水区面积越大，缓冲性能越好，浓度变异系数就越小；坡降越大，越有利于污染物迁移，其浓度变异系数就越大；农地和居民地占比越大，施肥、人为排放的污染物越多，污染物浓度越易受到人类活动的影响。由表4可见，对于面积小、坡降大的集水区(截流断面)污染物径流流失过程(特别是河道径流)涨退变化快、峰值多；而对于面积大、坡降小的集水区(万安断面)，河道径流的涨退变化较慢、峰值少。因此，前者需要较高的监测频次才能准确刻画污染物流失通量随时间的变化规律。大兴断面则有所不同，处于河谷平坝区，受居民地和农田两方面的影响均较大，故而氮磷流失通量的变异系数较高。

3 结 论

为探究LOADEST模型在丘陵小流域的适用性，优化污染物流失通量估算方法，本研究以四川省盐亭万安丘陵小流域为对象，估算基流条件下的氮磷流失通量及其年际变化，比较不同监测时间间隔的TN、TP流失通量估算值与实测值的差异，并分析其成因，结果表明：对于集水面积大、坡降小的河流断面，允许的最大监测时间间隔为20 d；而对于集水面积大、坡降小的河流断面，允许的最大监测时间间隔为40 d；LOADEST模型在TP流失通量估算中的表现优于TN；外推估算法不适用于该小流域的污染物流失通量估算。