CDP模型参数计算及取值方法验证
2021-06-01李清富匡一航
李清富, 匡一航, 郭 威
(郑州大学 水利科学与工程学院,河南 郑州 450001)
0 引言
ABAQUS软件在解决非线性问题上具有良好的适用性,其提供的混凝土损伤模型(CDP模型)最早由Lubliner等[1]提出,Lee等[2]引入刚度恢复的概念对CDP模型进行了改进。CDP模型通过损伤因子实现加载中材料刚度的折减,考虑了在循环荷载作用下混凝土裂缝开展、裂缝闭合及刚度部分恢复的行为,基本规则包括:屈服准则、流动法则和滞回规则[3-4]。CDP模型可用于往复荷载作用下混凝土结构和组合结构的受力行为模拟,可以较准确地模拟钢筋混凝土梁-柱组合结构的冲剪效应,在抗震分析方面广泛应用[5-7]。CDP模型需要用户自己提供混凝土的单轴应力-应变关系和设置部分模型参数。Rama等[8]使用混凝土塑性损伤模型评估不同等级混凝土的断裂性能,研究了膨胀角和偏心率等参数的影响,进一步提高了分析的准确性。方自虎等[9]通过对循环荷载作用下的混凝土构件进行模拟,分析了混凝土单轴应力-应变曲线对模拟结果的影响,推荐混凝土的受拉曲线取直线,其他部分使用规范中提供的公式。张劲等[10]和刘巍等[11]用各等级混凝土本构关系参数模拟结果与新旧规范中的混凝土本构曲线进行对比,验证了CDP模型参数的准确性。然而关于混凝土的应力-应变曲线截断处和损伤因子的取值范围的研究较少,因此,本文基于GB 50010—2010《混凝土结构设计规范》[12]中提供的本构关系,结合简支梁的试验结果对混凝土的应力-应变曲线截断处和损伤因子的取值范围进行标定,并选取3组试件进行建模分析,通过与试验数据对比,验证模型参数取值方法的合理性和准确性。
1 CDP模型参数的确定方法
1.1 混凝土应力-应变关系
CDP模型中采用的是混凝土在单轴受力状态下的应力和非弹性应变,非弹性应变根据混凝土的单轴应力-应变曲线换算。最具代表性的混凝土本构关系有3种:GB 50010—2010《混凝土结构设计规范》[12]、欧洲规范[13]和美国学者Kent-Park提出的应力-应变曲线方程[14]。欧洲规范没有明确给出单轴拉伸应力-应变曲线。混凝土结构设计规范在公式中引入了损伤演化参数,比Kent-Park模型收敛性更好。因此,采用《混凝土结构设计规范》提供的混凝土本构关系确定CDP模型中的参数。如图1所示,规范中的单轴应力-应变曲线按下式确定。
受拉情况:σ=(1-dt)Ecε;
(1)
受压情况:σ=(1-dc)Ecε。
(2)

图1 GB 50010—2010中混凝土单轴应力-应变曲线Figure 1 Uniaxial stress-strain curve of concrete in GB 50010—2010
1.2 损伤因子计算
直接将规范提供的损伤演化参数应用到CDP模型中会导致计算不易收敛。Sidoroff[15]提出应力作用在有损材料上产生的弹性余能与作用在无损材料上形式相同,进行力学分析时只需将弹性模量改为有损状态时的弹性模量。Sidoroff基于此假设提出的损伤因子计算方法如式(3)所示。经验证,这种方法适用于CDP模型损伤因子的计算。
(3)
式中:σ和ε由式(1)和式(2)计算所得;E0为混凝土的初始弹性模量。
1.3 CDP模型参数

(4)


图2 混凝土塑性损伤模型受压应力-应变关系Figure 2 Uniaxial compression stress-strain curve of CDP
图3为CDP模型各项拉应变之间的关系,受拉开裂应变可依下式计算:
(5)


图3 混凝土塑性损伤模型受拉应力-应变关系Figure 3 Uniaxial tensile stress-strain curve of CDP
对于普通混凝土,CDP模型的其他参数的推荐值见表1。膨胀角和偏心率是和屈服面流动法则相关的参数。K为混凝土屈服形态的影响参数。fb0为混凝土双轴抗压强度,fc0为单轴抗压强度,两者的比值取规范推荐值。μ为CDP模型定义的黏性参数,μ越大计算越容易收敛,越小计算精度越高,取0.000 5时可以同时满足精度和收敛性的要求。
2 模型参数的标定
CDP模型对于混凝土的极限拉压非弹性应变并未做出规定,为此需要对混凝土拉压应力的截断处进行标定。以文献[16]中的1根试验梁STEEL-40S为例,采用上述表达式计算相关参数进行模拟分析,同时对混凝土拉压应力的截断处进行初步的标定。

表1 CDP模型材料参数Table 1 Material parameters of CDP
2.1 试验梁及计算模型
简支梁STEEL-40S的截面尺寸、加载方式和配筋见图4,受压筋、受拉筋和箍筋均采用SD400 D10钢筋,其材料参数见表2。浇筑混凝土时预留立方体伴随试块,试块抗压强度平均值fcm=40.9 MPa,换算后可得立方体抗压强度标准值fck=27.3 MPa。CDP模型参数计算时采用立方体抗压强度标准值,计算得到损伤因子及相关参数见表3、表4。
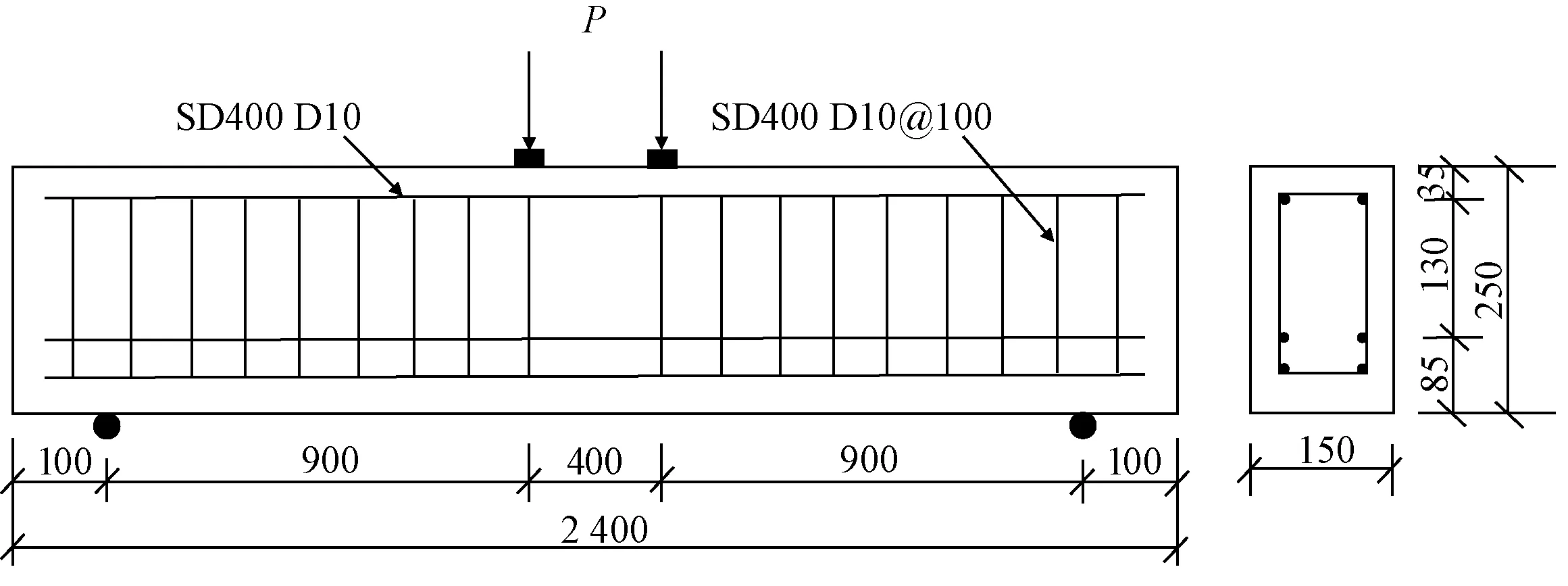
图4 简支梁配筋详图(mm)Figure 4 Detailed view of the beam and specimen cross-section(mm)

表2 钢筋的材料参数Table 2 Material parameters of reinforcement

表3 混凝土受压参数Table 3 Compressive parameters of concrete
根据简支梁STEEL-40S的几何尺寸、加载方式和约束位置建立模型,混凝土的材料属性采用表3、表4中的参数,钢筋的本构模型采用双斜线模型。混凝土单元类别为C3D8实体单元,钢筋单元类别为T3D2桁架单元,单元尺寸均为50 mm。加载点和支座处通过设置钢垫片避免应力集中的现象,采用位移控制加载提高计算的收敛性。

表4 混凝土受拉参数Table 4 Tensile parameters of concrete
2.2 数值计算结果及分析
对xc的最大值xc,max和xt的最大值xt,max取不同的值,研究混凝土拉压应力-应变曲线截断处取值和损伤因子取值对计算结果的影响。当xc,max和xt,max取值小于3时,有限元模型的荷载-跨中挠度曲线与试验值差异较大,对xc,max分别取3、6、9、15、20,对xt,max分别取3、6、10、20、40建立有限元模型进行分析。简支梁STEEL-40S开裂荷载的试验值为13.28 kN,极限荷载的试验值为56.91 kN,达到极限荷载时的挠度为40.51 mm。图5和表5为xc,max和xt,max9种取值组合的荷载-跨中挠度曲线的计算结果与简支梁试验数据的对比。当xc,max=20,xt,max=3 时,极限荷载的理论值为60.69 kN,达到极限荷载时的挠度为14.20 mm,不能反映试验真实情况。当xt,max=40,xc,max=3时,开裂荷载的理论值与真实值相差3.26 kN,在跨中挠度100 mm以内荷载-跨中挠度曲线没有出现下降段。当xt,max=40时,5组模拟所得的荷载-跨中挠度曲线在弹性范围内可以较好地反映真实情况,开裂荷载的计算值均为16.54 kN,与真实值接近。当xt,max=40,xc,max=20时,受拉损伤因子和受压损伤因子的取值均大于0.95,开裂荷载、极限荷载以及极限荷载对应的跨中挠度的理论值与试验值的相对误差均小于5%,吻合性较好,曲线趋势可以反映试验真实情况。

图5 不同截断值荷载-跨中挠度曲线Figure 5 Load-span deflection curves at different cutoffs
3 CDP模型在结构分析中的应用
在初步验证混凝土的应力-应变曲线截断处取值的基础上,以文献[16-18]中的试验梁STEEL-60S、试验梁PKJ1和剪力墙CW-1为例建立有限元模型,以本文推荐的值和表达式计算模型参数,受拉受压损伤因子取值大于0.95,混凝土的应力-应变曲线截断处也与之对应。将模型计算所得的荷载-位移曲线和试验值比较,进一步检验CDP模型参数取值和计算方法。
试验梁STEEL-60S的有限元模型如图6(a)所示,底部混凝土的受拉损伤因子达到预先设定的最大值,出现了严重的受拉破坏,分配梁加载点附近的混凝土受压损伤因子达到预先设定的最大值,与试验梁的破坏现象基本吻合。图6(b)为荷载-位移曲线试验值与计算值的对比,两者趋势基本一致;开裂荷载的计算值为19.82 kN,与试验值相差2.37 kN;极限荷载的计算值为62.21 kN,与试验值相差1.68 kN。

表5 开裂荷载和极限荷载理论值Table 5 The first crack moment and the experimental and analysis values of the maximum moment
如图7所示,试验梁PKJ1的有限元模型从底部出现垂直裂缝,随后斜裂缝自两端向加载点迅速发展,最终因为加载点附近的混凝土压碎而破坏,与试验梁发生剪压破坏的实际情况相符。开裂荷载的试验值为29 kN,计算值为31.22 kN,试验值比计算值低7.1%。极限荷载的试验值为140 kN,计算值为137.58 kN,试验值比计算值高1.7%。有限元模型计算所得的荷载-位移曲线在弹性阶段、屈服阶段、破坏阶段与试验数据吻合。
剪力墙CW-1的有限元模型的混凝土开裂损伤如图8(a)所示,在往复水平力的作用下,有限元模型出现从下至上、由墙外向墙内发展的水平裂缝,随着荷载循环次数的增加,水平裂缝向下发展成为斜裂缝,与试验现象完全吻合。有限元模型的水平力-位移曲线与试验值的对比如图8(b)所示,有限元模型达到峰值荷载后,水平力不再增加,而顶点的水平位移随着循环次数的增加逐渐变大;计算所得的滞回曲线饱满,趋势与试验曲线一致;正反向屈服荷载的平均值为320.1 kN,比试验值低3.9%;正反向峰值荷载平均值为414.9 kN,比试验值高4.3%。

图8 剪力墙 CW-1有限元模型及数值对比分析Figure 8 Shear wall CW-1 finite element model and numerical comparison analysis
4 结论
(1)根据本文推荐的损伤因子计算式,将规范提供的混凝土应力-应变曲线应用到CDP模型,得到的模型参数是准确可靠的,可用于混凝土构件的开裂验算和承载力分析。
(2)当受拉受压损伤因子取值大于0.95,混凝土的应力-应变曲线截断处也与之对应时,开裂荷载和极限荷载有限元分析的结果与试验值相对误差较小。
(3)CDP 模型没有考虑钢筋和混凝土之间存在的黏结滑移现象,有限元模型的计算结果与试验结果存在差异,但结果可以满足工程精度要求。
