利用动态圆求解粒子在电磁场中的运动问题

李开玮

（广东理工学院工业自动化系，广东 肇庆 526100）

电荷在电磁场中运动时，常常考察不同速度的粒子流在有限区域边界中的运动轨迹，求解的问题一般有以下几类：1）运动时间最值；2）离开边界时出射点符合一定条件的粒子问题；3）粒子获得动能最值。该类问题属于动态问题，情景比较复杂，笔者在研究时发现许多情况下，利用动态圆能够描绘出随参数条件变化的动态轨迹图像，观察到问题的临界情形，对解题提供一个很好的突破口[1-4]。接下来将以几道真题的解析来讨论动态圆的运用技巧，给学生在思考该类问题时提供一些思路和启发。

1 真题研究

1）例1（2020 年全国Ⅰ卷18 题）一匀强磁场磁感应强度大小为B，方向垂直于纸面向外，其边界如图1 中虚线所示，为半圆，ac、bd与直径ab共线，ac间的距离等于半圆的半径。一束质量为m，电荷量为q（q＞0）的粒子，在纸面内从c点垂直于ac射入磁场，这些粒子具有各种速率。不计粒子之间的相互作用。在磁场中运动时间最长的粒子，其运动时间为（ ）。

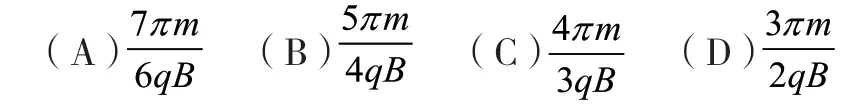
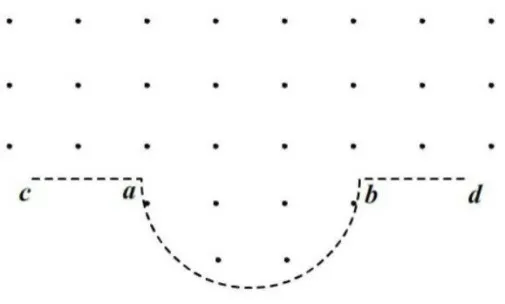
图1 例1 示意图

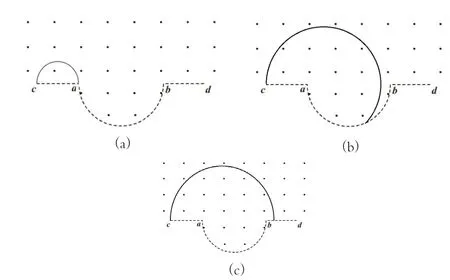
图2 随着半径变化，粒子不同运动轨迹

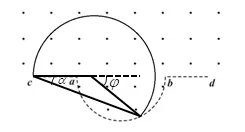
图3 出射点在半圆上时的动态圆示意图

若没有考虑到动态圆中相切的情形，可以采用常规的代数方法求解，如图4所示，连接半圆圆心与出射点，根据三角形余弦定理有：

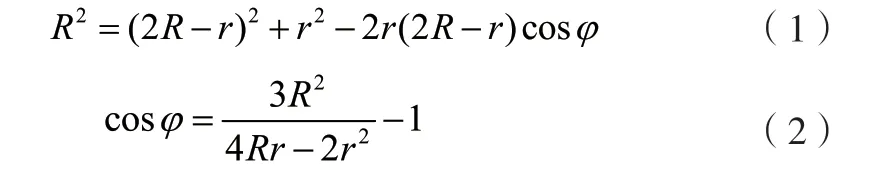
由式（2）得，当r=R时，φ取最大值π/3，此时圆心角最大。

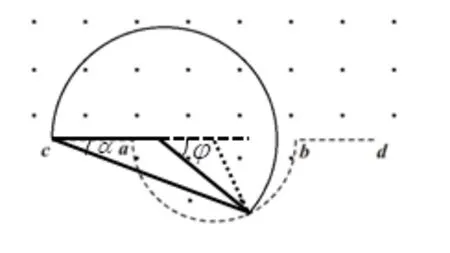
图4 代数法求解示意图

2）例2（某省高考模拟题）如图5 所示，一平行板电容器水平放置，在其两极板中央分别开了一条上下正对的直狭缝，以上极板的狭缝所在直线为x轴，竖直向上为y轴建立一竖直平面内的直角坐标系，质量为m，电量为-q的粒子流从下极板的狭缝沿竖直向上方向进入电容器，粒子速率各不相等，粒子经过电容器的两个狭缝后进入第一象限，在第一象限内，某一片区域有垂直纸面向里的匀强磁场B，点为磁场边界上的一点。电容器上板比下板电势高，电势差为U，忽略粒子的重力及粒子间相互作用，且。

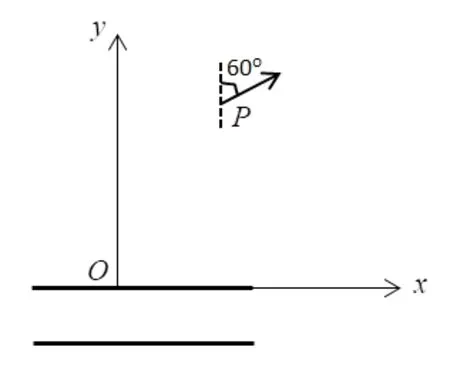
图5 例2 示意图

①若某粒子进入下极板时初速度大小为v0，则当此粒子进入磁场区域后，作圆周运动的半径为多少？

③为满足第②问中的粒子运动情况，第一象限内的磁场面积至少是多大？

解析：①该问比较简单，做法常规，粒子在离开电容器时速度为v，根据能量转化关系：

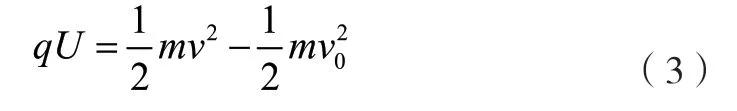
粒子在磁场中受洛伦兹力作用，作圆周运动：

由式（3）、式（4）可得圆周运动半径为：

②根据洛伦兹力方向，粒子进入磁场区域向右偏转，部分粒子能到达P点，且过P时速度斜向右上方与竖直方向夹角60o，根据圆的几何特点，过P点作垂线垂直于速度方向，同时粒子进入磁场时速度方向为竖直向上，也作垂线垂直于入射速度方向，圆的半径应处处相等，根据这些特点作出粒子运动轨迹，如图6 所示，E点应为轨迹圆心，根据几何关系，DE 为水平方向，应为等边三角形，因此有：

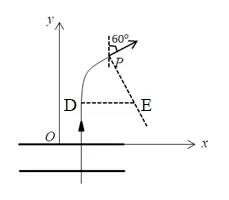
图6 能到达P 点粒子运动轨迹

由式（5）、式（6）可得：

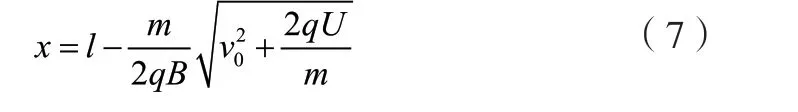
③根据第②问中能到达P点粒子运动轨迹图像，作出不同横坐标x处入射的粒子运动轨迹图，如图7 所示，当v0=0 时，圆周运动半径最小，入射点横坐标最大，即点A，入射点横坐标最小为x=0，即点B，O1A 与O2B 均为水平方向均为等边三角形，因此B、A、P 三点共线，故磁场的边界为BA、，根据式（5）、式（6），粒子运动的最小半径R1，最大半径R2分别为：

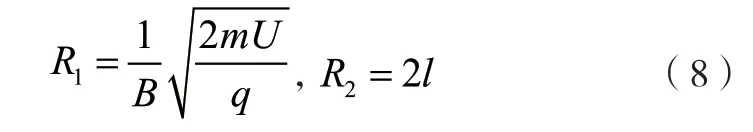
根据图7中几何知识可得，磁场区域最小面积为：

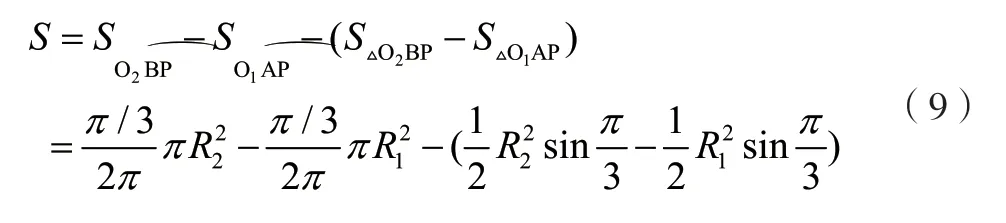
由式（8）、式（9）得：

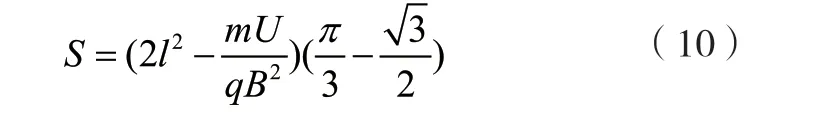
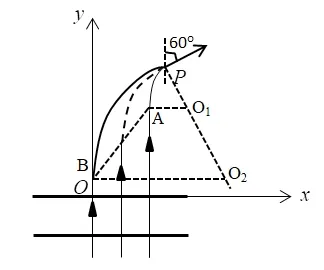
图7 不同位置入射粒子在磁场区域轨迹示意图

2 结语

本文通过两道真题解析，讲述了动态圆在解带电粒子在电磁场中运动问题的技巧，有助于提高学生作图，利用几何图像得到临界条件的能力，加强学生运用数形结合处理问题的思维。