圆支圆板在动爆冲击波作用下的动力响应

荣吉利，刘东兵，赵自通，王玺，吴志培，李富荣

(1.北京理工大学 宇航学院，北京 100081；2.北京航天发射技术研究所，北京 100076； 3.中国运载火箭技术研究院，北京 100076)

随着现代兵器科学技术不断地发展，涌现出了各种性能高、威力大的武器.作为衡量战斗部杀伤威力的主要因素之一，爆炸冲击波对导弹发射车等装甲车辆的毁伤往往更具无形的破坏效应.现代化武器的战斗部在爆炸的瞬间常伴有很高的运行速度，例如地空导弹的运行速度就可达到2～4倍的音速，该运行速度对爆炸冲击波的威力有着十分巨大的影响[1].因此研究考虑装药运行速度的爆炸冲击波作用下装甲防护材料的动力响应特性对于防护工程的发展及应用有十分重要的意义.

现阶段学者们对爆炸冲击荷载作用下防护材料的动态响应特性的研究，绝大部分是以不考虑装药运行速度的静爆冲击荷载为基础，如李向荣等[2]通过数值模拟研究了静爆冲击荷载对装甲车辆底板的毁伤作用，得到了V型底装甲结构的最优角度为10°.王显会等[3]研究了蜂窝夹层结构的抗静爆冲击波性能，得出结论：横向布置蜂窝夹层结构较纵向布置蜂窝夹层结构的吸能性更好.在动爆冲击载荷方面，已有部分学者考虑了装药的运行速度并对其进行了相关研究，如继张光莹等[1]2008年提出动爆冲击波特性分析方法之后，吕中杰等[4]对动爆爆心位置的定位做了探究.蒋海燕等[5]和聂源等[6]又通过数值仿真的方法研究了考虑装药速度的动爆冲击波场的分布规律，并结合数据拟合建立了理论工程计算模型.而目前学者们对于动爆冲击荷载作用下防护材料的动力响应特性的研究较少.

本文通过Autodyn软件进行建模分析，研究考虑装药运行速度的动爆冲击波对装甲钢圆形靶板的毁伤效能，分析装药运行速度对沿其速度方向爆炸冲击波威力的影响规律.并基于仿真结果，建立动爆冲击波作用下周围固定圆形靶板的中心挠度计算模型，最后对建立的计算模型进行仿真验证.

1 静爆冲击波理论基础

爆炸冲击波是战斗部在空中爆炸和地面爆炸时的主要杀伤方式，对于爆炸冲击波杀伤破坏能力的定量描述，主要有冲击波超压峰值、正压持续时间和比冲量.

1.1 冲击波超压峰值和正压持续时间

根据爆炸相似律建立的经验公式是工程中常用的爆炸冲击波计算方法，关于冲击波超压峰值和正压持续时间的理论计算公式，比较经典的有Henrych公式[7].

1.1.1超压峰值

(1)

1.1.2正压持续时间

(2)

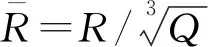
1.2 比冲量

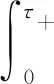
2 数值仿真

2.1 仿真模型有效性验证

2.1.1模型建立

为验证采用Autodyn软件进行数值仿真的有效性，建立模型模拟静止球形裸装药在无限空气中的爆炸冲击波传播过程，并将仿真得到的冲击波超压峰值和Henrych经验公式值进行对比，以此验证数值仿真的有效性.建立如图1所示的二维楔形空气模型，长度2 000 mm，网格为1 mm，在距离爆心600 mm远处每隔200 mm设置共7个测量点.爆炸源采用TNT球形裸装药，当量为3.494 kg，装药半径80 mm，TNT端点的起爆方式设置为单点起爆.

图1 冲击波验证模型Fig.1 Shock wave validation model

对空气和TNT均采用Euler单元.

2.1.2材料模型

仿真验证中涉及空气和TNT两种材料.其中，空气使用在Boyle定律和Gay-Lussac定律基础上推导而来，理想气体状态方程 (Ideal Gas)[9]描述为

p=(γ-1)ρe

(3)

式中：p为气体压力;γ为多方气体指数;ρ为气体密度;e为比内能.对于空气有γ=1.4，ρ=1.225 kg/m3，e=2.068×105kJ/kg.

TNT使用JWL状态方程[10]:

(4)

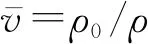
表1 TNT的JWL状态方程参数

2.1.3结果分析

从图2所示不同测量点的超压峰值变化曲线可以看出，随着距离起爆中心距离的增大，各位置处的冲击波超压峰值呈减小趋势.数值仿真值和Henrych公式值的超压曲线变化趋势完全一致，且两种计算方式的误差也在可控误差范围之内，并随比例距离的增大，数值仿真值和经验公式值之间的误差逐渐减小且经验公式的理论计算值略小于模拟仿真值，与文献[7]的结果一致吻合.因此利用非线性显式动力学软件Autodyn进行数值仿真具有真实性和有效性.

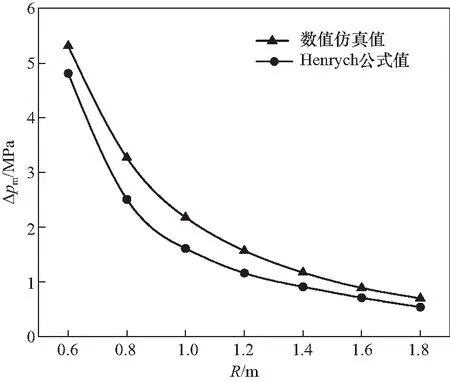
图2 各测量点的超压峰值曲线Fig.2 The peak curve of overpressure at each measuring point

2.2 装甲钢圆板在动爆荷载作用下的仿真分析

2.2.1模型建立

由于研究问题具有中心对称性，因此对三维问题可简化为二维问题并利用Autodyn-2D进行建模求解.空气域尺寸1 000 mm×400 mm，网格尺寸2 mm，采用Euler单元，四周设置边界流出条件(Flow_Out)，以模拟无限空气域.炸药使用TNT球形裸装药，当量3.494 kg，装药半径80 mm.圆形靶板材料采用RHA(装甲钢)，半径400 mm，厚度8 mm，采用Lagrange单元，周围设置固定边界条件.装甲钢靶板与空气之间的流固耦合作用设置为Lagrange/Euler-Automatic.考虑到模型的轴对称性，以y轴为对称轴建立1/2模型，且设置对称边界条件.装药采用单点起爆方式，在装甲钢靶板正上方500 mm处起爆.

给TNT球形裸装药分别施加0(静爆)，200，500，800，1 000，1 200，1 500，1 700 m/s的运行速度，研究动爆冲击波作用下装甲钢圆形靶板的动态响应特性.有限元模型如图3所示.

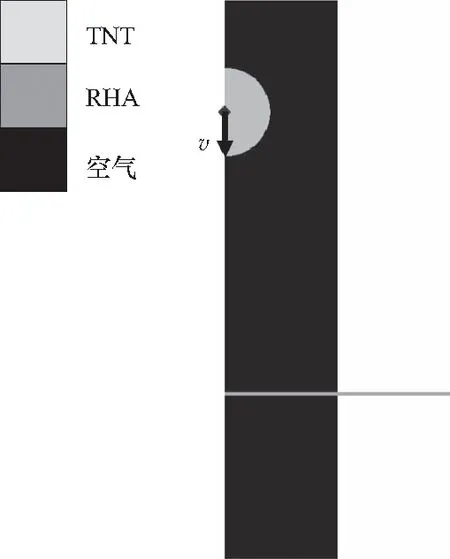
图3 二维计算模型Fig.3 Two-dimensional finite element calculation model

2.2.2材料模型

仿真模拟涉及空气、TNT和RHA(装甲钢)三种材料，其中空气和TNT分别采用2.1.2中的Ideal Gas和JWL状态方程描述，且参数相同.RHA采用Shock状态方程描述[11]为

p=pH+ГP(e-eH)

(5)

式中：ГP为Gruneisen常数；压力pH和能量eH分别为

(6)

(7)

式中：μ=ρ/ρ0-1，ρ0为材料初始密度；ρ为材料密度；c0为材料声速.具体参数如表2所示.

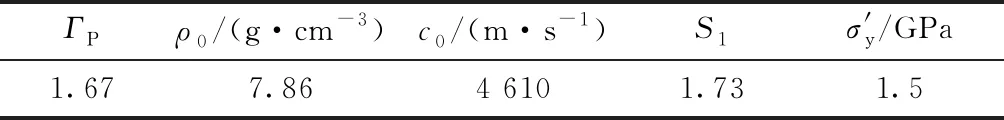
表2 RHA材料参数

2.2.3仿真结果

表3所示是不同装药运行速度的动爆冲击波在距爆心500 mm的参数，Δpm,v和τ+,v是动爆冲击波沿装药运动速度方向的超压峰值和正压持续时间.从表中可以看出，动爆冲击波的超压峰值随装药运动速度的增大而增大，装药运动速度为1 700 m/s时，动爆冲击波超压峰值达到了静爆冲击波超压峰值的3倍多；动爆冲击波的正压持续时间随装药运动速度的增大反而有减小趋势，装药运动速度为1 700 m/s时，动爆冲击波正压持续时间约为静爆冲击波正压持续时间的66%.由此可以得到：装药爆炸瞬间的运行速度加快了沿装药运行速度方向爆炸冲击波的传播速度，极大地提高了沿装运行药速度方向爆炸冲击波的威力.

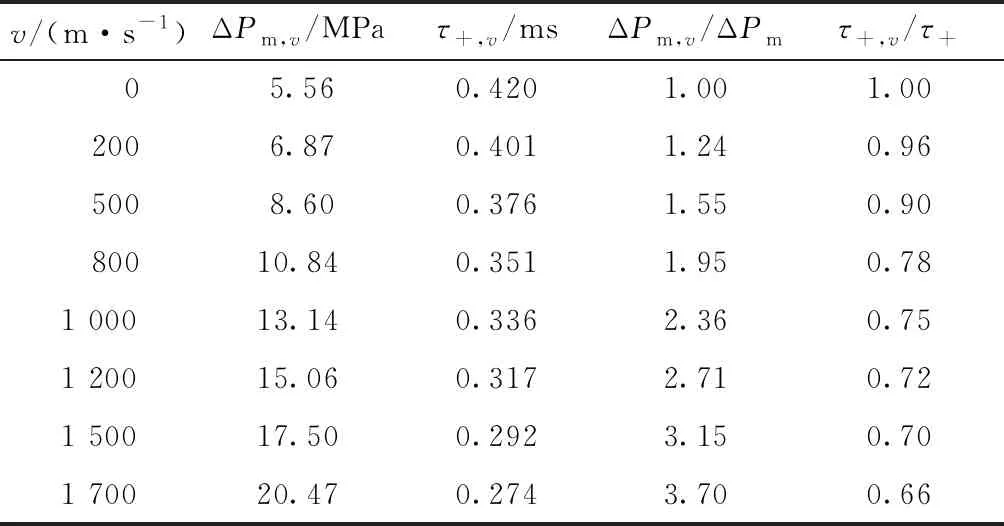
表3 R=500 mm处的仿真结果

图4所示为不同装药速度动爆冲击荷载作用下圆形靶板的变形图，直观地体现了圆形靶板的中心挠度随装药运行速度增大而增大的过程，当装药运行速度为1 700 m/s时，靶板中心的挠度值达到了95.51 mm，约为静爆冲击波作用下靶板中心挠度的3倍.由图5靶板中心挠度随冲击波传播时间t的变化曲线可以看出，随冲击波传播时间的增大，靶板中心的挠度逐渐增大，并在一定时间后达到最大值，且该时间随装药运行速度的增大而有减小趋势，随后靶板中心挠度又略有减小且保持不变，考虑到这是由于靶板材料的弹塑性变形引起.

图4 靶板变形云图Fig.4 Target plate deformation diagram

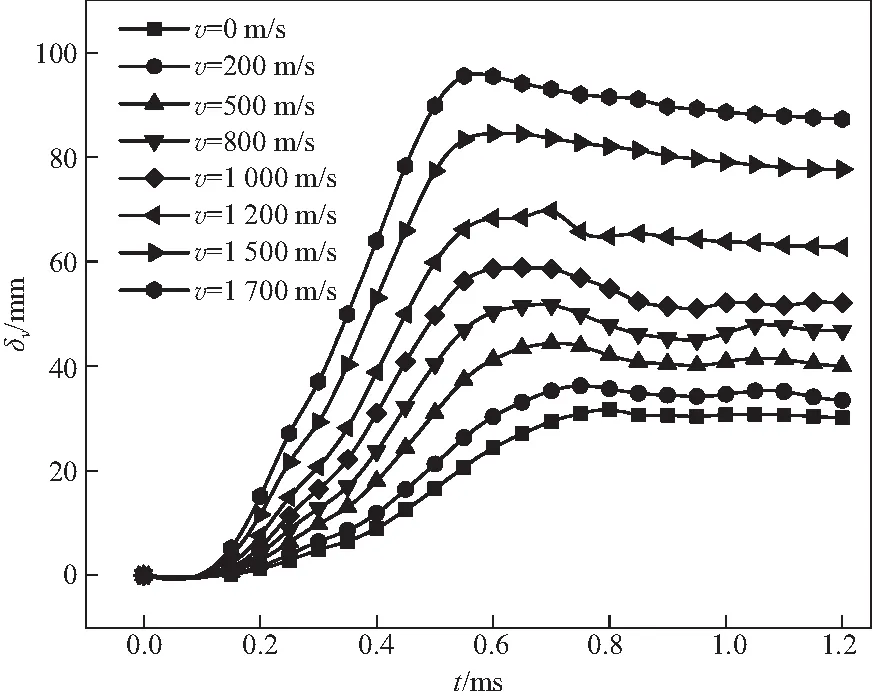
图5 靶板中心挠度随时间变化曲线Fig.5 Target deflection curve with time

3 动爆冲击波作用下圆板中心挠度理论计算模型建立

由于爆炸冲击波可视为一种不连续的峰在介质中传播，这个峰使得传播介质的温度、压强等参数发生跳跃式的改变，因此类似于板状结构的防护材料在爆炸冲击荷载作用下的变形和破坏表现为同应力、应变率等参量之间的复杂关系，其动力响应过程也随之变得非常复杂，难以得到精确的解析解.Jones[12]根据实验结果对实验数据进行拟合得到了静爆冲击荷载作用下完全固定圆板的中心挠度计算公式:

(8)

(9)

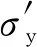
当TNT当量为3.494 kg时，根据式(1)(2)和式(8)(9)，可计算得到仿真所采用装甲钢圆形靶板的中心挠度为33.79 mm.与装药运行速度为0时的仿真结果相差6.3%.明显，沿装药运行速度方向动爆冲击波的威力随装药运行速度的增大要远大于静爆冲击波的威力.因此静爆冲击波作用下圆板中心挠度的理论计算公式不再适用于动爆冲击波作用下圆板中心挠度的计算.考虑装药运行速度，建立动爆冲击波作用下圆形靶板中心挠度的理论计算公式，并对建立的理论计算模型进行仿真验证.

陈龙明等[13]在描述动爆冲击波超压时引进修正因子η使得冲击波超压峰值为

Δpm,v=Δpmη

(10)

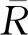
(11)

式中：c0为声速，在空气中取c0=340 m/s.

对正压持续时间，根据表3的仿真结果，可通过数据拟合得到动爆正压作用时间与静爆正压作用时间之间的关系式为

τ+,v=(-0.000 2v+0.992 2)τ+

(12)

式中：τ+,v为动爆正压作用时间，τ+可根据式(2)求得.

因此，根据式(8)～(12)可以得到动爆冲击荷载作用下圆形靶板中心挠度的理论计算公式为

(13)

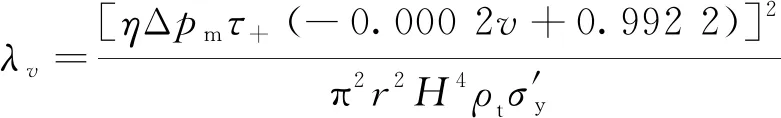
(14)

式中:λv为考虑装药运行速度的量纲一系数，由式(14)计算得到.

为了验证建立的理论计算模型的可靠性，建立与图3所示相同的模型，另取装药运动速度分别为100，300，600，900，1 100，1 400 m/s，通过数值仿真和建立的理论计算模型分别计算动爆冲击荷载作用下装甲钢圆形靶板的中心挠度值，并比较二者间的误差，如表4所示.

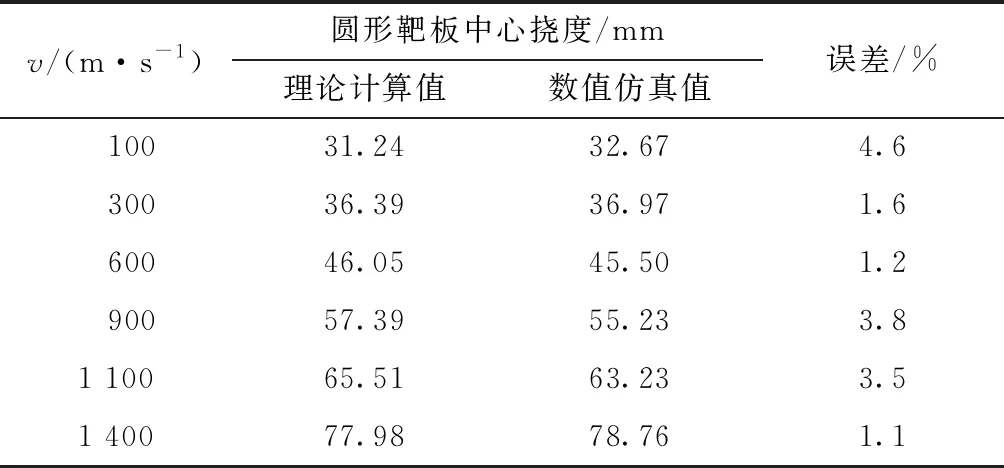
表4 理论计算与仿真结果对比

通过对6组数据的误差分析，可以看出：采用建立的理论计算模型计算得到的圆形靶板中心挠度值，与采用Autodyn得到的数值仿真值之间的误差均小于5%，误差平均值为2.6%，对比结果较为理想，因此验证了建立的理论计算模型的可靠性，可为实际工程中的相关计算提供理论基础.

4 结 论

使用Autodyn软件对动爆冲击荷载作用下装甲钢圆形靶板的动态响应进行了数值计算，分析了装药运行速度对爆炸冲击波和冲击波作用下靶板变形的影响规律.具体有：沿装药运行速度方向的爆炸冲击波的超压峰值随装药运行速度的增大而增大，冲击波传播速度随装药运行速度的增大而加快；圆形靶板的中心挠度随装药运行速度的增大而增大，装药运行速度为1 700 m/s时，靶板中心挠度为95.51 mm，是静爆冲击荷载作用下靶板中心挠度的3倍.并基于仿真结果，建立了动爆冲击荷载作用下圆形靶板中心挠度的理论计算模型，通过取不同装药速度，对理论计算值和数值仿真值进行误差分析，结果表明建立的理论计算模型能得到较为理想的结果，可为工程计算提供理论依据.