基于仿真和智能算法骨骼肌超弹性本构参数的反演方法研究1)

李 洋 桑建兵 敖日汗 马 钰 魏新宇

(河北工业大学机械工程学院,天津 300130)

引言

骨骼肌约占生物体重的40%[1],是维持生物基本运动最重要的生理软组织,而骨骼肌的损伤会导致人类行为严重受限,如常见的临床病例:中风、截瘫等[2].在对骨骼肌研究中,软组织的本构关系可能是最基本和最关键的,因为其可以建立可靠的数学或计算模型.由于骨骼肌组织的特殊特性(各向异性[3]、非线性[4]、超弹性[5]、时间依赖性[6]) 的存在,骨骼肌组织的力学特性的表征具有很大的挑战性.全面了解骨骼肌的组成行为,对于更好地了解骨骼肌的生物学特性,提高肌肉疾病和损伤的治疗水平具有重要意义.许多学者进行了大量的实验来研究骨骼肌的生物力学特性,包括压缩[7]、拉伸[8]、应力松弛[9]等.王宝珍等[10]对猪后腿肌肉进行冲击压缩实验,并利用改进后的分离式Hopkinson 压杆技术获取了不同加载方向和不同应变率下的应力应变数据.Mohammadkhah 等[11]对新鲜鸡胸大肌进行了加载方向平行于纤维方向和垂直于纤维方向以及加载方向与纤维方向成45°的单轴准静态压缩和拉伸实验,证明鸡肌肉的力学行为是非线性和各向异性的.B¨ol 等[12]使用3 种不同的加载模式对肌肉组织进行了一系列实验.结果表明,纤维方向对压缩应力有各向异性贡献.如果有可靠的正问题模型,反问题分析是系统的识别材料性质的有效手段[13].Takaza 等[14]证明了反向有限元方法在确定材料性能方面的有效性.Silva 等[15]通过逆有限元方法并结合优化算法获得了女性耻骨联合肌肉的主动和被动力学特性.虽然现有的研究在识别本构参数方面取得了进展,但现有预测的准确性还有待进一步提高.

随着人工智能技术(AI)的发展,机器学习(ML)作为AI 的一个分支已被广泛应用于生活中的各个领域,如数据融合和识别[16-17]、医学检测[18-19]、流体力学[20-22]和固体力学中[23-24].ML 在模拟输入和输出变量之间的非线性相关性方面具有很高的效率,并且已经被用于预测生物软组织的力学特性.Liang等[25]利用支持向量机模型和有限元方法相结合来预测主动脉瘤的风险,并取得了良好的效果.Lu 等[26]提出了一种基于动态多体方法和神经网络分析的创新方法,建立了基于有限元的软骨神经网络模型.Liu等[27]对牛的肌肉组织进行了无约束压缩实验,并利用了改进后的小生境遗传算法预测了肌肉组织的本构参数.通常AI 的成功归结于大规模的数据集,然而许多现实应用的场景例如医学,军事等领域,因为隐私或者安全等因素不允许收集足够多的数据集,所以对于小样本的学习便成了当今AI 领域的热点问题.Koch 等[28]将深度学习与小样本学习结合起来,提出了一种新的卷积神经网络模式来学习成对的样本中与类别无关的变量.Liu 等[29]基于BP 神经网络,建立了一个可靠的正问题神经网络来代替有限元方法收集样本,来缩短收集样本的时间,也为解决小样本学习问题提供了新的想法.而简单的机器学习模型对小样本学习也会有良好的效果.因此,本研究考虑将机器学习的方法应用于骨骼肌的本构参数的预测,分别提出了两种反问题求解方法,一种是将K 近邻模型(KNN)与有限元方法(FEM)相结合,另一种是将支持向量机回归模型(SVR)与有限元方法相结合.在本研究中,通过训练和测试Liu 等[27]收集的数据集,证明了所提出的两种反问题求解方法的有效性.本研究还进一步对比了所提出的两种方法,对比结果表明,利用K 近邻模型结合有限元方法是预测骨骼肌本构参数的更精确有效的方法.

1 有限元模型的建立

骨骼肌的在生理学上的数学表述是一项复杂的任务,考虑到其大变形行为,骨骼肌的材料特性常被模拟为各向异性,非线性和超弹性.各向异性超弹性模型可以很好模拟骨骼肌的力学行为,其本构方程如下[30]

各向异性骨骼肌中本构参数的确定是一项具有挑战性的任务,由于骨骼肌组织的高含水量,骨骼肌通常被认为是不可压缩的物质[32].所以本文提出的反演程序预测的本构参数包括:C10,k1,k2和κ.

图1 给出了为模拟骨骼肌单轴压缩试验的有限元模型.骨骼肌被建模为超弹性各向异性材料.有限元网格由3375 个八节点六面体单元和4096 个节点组成.八节点六面体单元相对于四面体单元,增加了节点的数目,可以显著的提高计算精度.因为拉伸试验机顶部和底部的压板是由钢制成的,相比于新鲜的骨骼肌组织要硬的多,所以在有限元仿真中他们被定义为刚体.在压板与骨骼肌组织样本之间设置了摩擦系数以更准确的模拟实验.

图1 模拟实验设置的骨骼肌有限元模型Fig.1 Finite element model of skeletal muscles for simulating experiment

2 K 近邻与支持向量机预测模型构建

KNN 是一种常用的有监督学习的机器学习算法,因为其具有从高维特征空间中恢复相似实例的简单性和直观性,所以具有广泛的应用前景.在KNN模型中,KNN 对于给定测试样本,基于距离度量找出训练集中与其最靠近的K个训练样本,然后基于这K个“邻居”的信息来进行预测[33].KNN 模型的核心问题是K值的选取以及距离函数的选择.在本研究中,通过大量的数值实验,最终确定K=3.待求样本的状态向量与已知样本的状态向量之间的距离量度表示二者之间的相似程度.常见的KNN 模型的距离函数有欧式距离、曼哈顿距离、马氏距离、切比雪夫距离等.在本研究中使用的欧氏距离公式如下:假设待求样本的状态向量为x=(x1,x2,···,xn),已知样本的状态向量为y=(y1,y2,···,yn),则其之间的距离d为

支持向量机(SVM)也是一种常用的机器学习算法,具有很强的非线性数据处理能力.而SVR 是支持向量机算法通过非线性回归分析的延伸[34],是解决回归问题的一种有效方法.支持向量机回归模型利用核函数将非线性问题转化为高维空间的线性问题,是替代高维空间复杂计算的一种非常有效的方法[35].常见的核函数有线性核函数、多项式核函数、径向基核函数(radical basis function,RBF).其中应用最广泛的是径向基核函数,其已广泛应用在机械设备故障识别预测[36].RBF 定义为

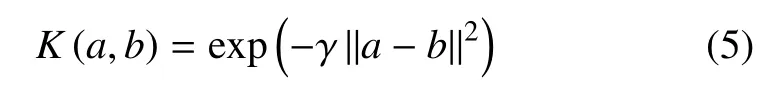
这是一个从0 变化到1 的钟形函数.其中a和b代表样本向量,γ 为超参数.

3 预测结果与讨论

在本研究中,Liu 等[27]对骨骼肌进行单轴压缩实验中获得的名义应力和主伸长数据集被分成两个子数据集,分别对应于加载方向平行于纤维方向和加载方向垂直于纤维方向.参数空间的必要参数为4 个,分别为C10(取值范围0.2～1.5 kPa),k1(取值范围0.05～0.4 MPa),k2(取值范围10～60),κ(取值范围0.04～0.32).本研究在参数空间中分别以固定增量采集了250 组骨骼肌超弹性本构参数以使得采集到的本构参数能够充分代表整个参数空间,其中C10增量为5.0×10-3kPa,k1增量为1.4×10-3MPa,k2增量为0.2,κ 增量为1.12×10-3.将收集到的骨骼肌组织的本构参数通过建立的有限元模型得到了相应的名义应力和主伸长.之后以有限元模型收集的名义应力作为输入,以相应的本构参数作为输出分别构建KNN模型和SVR 模型.为了更准确,快速地进行回归,本研究分别对名义应力和骨骼肌组织的本构参数进行归一化处理

其中,X′是归一化后的取值,X是实际取值;Xmax,Xmin分别对应于名义应力和骨骼肌组织的本构参数的最大值和最小值.当训练完成后,将骨骼肌压缩实验中获得的名义应力数据集分别输入两个模型,最终得到实验样本的本构参数.

为了进行监督学习,需要选择合适的训练和测试数据进行预处理.训练集用于构建KNN 和SVR模型,测试集用于验证模型的泛化能力.训练集的大小必须代表整个数据集的特征.训练集数目太少可能导致模型的学习能力差,而训练集数目太多很可能导致验证困难并导致计算时间过长.在本研究中,80%的有限元收集到的数据被分给训练集,其余20%被分配给测试集[37].图2 给出了本文中提出的两个反向识别本构参数反演方法的流程图.

图2 本研究中提出的本构参数识别方法流程图Fig.2 Flow chart of the parameter identification method proposed in this study

基于Liu 等[27]得到的骨骼肌压缩实验数据,本研究对利用提出的参数识别程序得到的本构参数进行处理,以获得一组本构参数,这些参数既可以表示加载方向平行于纤维方向,又可以很好地表示加载方向垂直于纤维方向.在训练集完成之后,测试集的数据用来评估KNN 模型和SVR 模型的准确性,并比较本构参数的真实值和预测值.在本研究中,选用了决定系数(R2)作为预测值准确率的指标.R2反映了因变量的所有变化可以通过回归关系由自变量所解释的比例,即利用数据的平均值作为误差基准,观察预测误差与平均参考误差的偏离程度.R2为

式中,N是样本的数量,yi代表真实值,ypred代表预测值,代表真实值的平均值.图3 描绘了测试集中本构参数的真实值与预测值准确率的直方图.从直方图中可以看出,无论是KNN 模型还是SVR 模型测试集中各本构参数的准确率都很好.

图3 KNN 模型和SVR 模型测试集预测准确率比较Fig.3 Comparison of test set prediction accuracy between KNN model and SVR model

图4 给出了当加载方向平行于纤维方向和加载方向垂直于纤维方向时,利用KNN 模型获得的本构参数的计算响应曲线和实验曲线的比较以及仿真加载过程的名义应力云图.从图4 可以看出名义应力和主伸长之间存在非线性关系,并且名义应力随着主伸长的增大而增大,无论加载方向平行于纤维方向还是垂直于纤维方向,利用KNN 模型预测的骨骼肌本构参数的响应曲线与实验曲线吻合良好.通过比较图4(a) 和图4(b) 可以发现,当加载方向垂直于纤维方向时,骨骼肌组织对压缩变形表现出更强的抵抗力.

图4 利用KNN 模型获得的计算响应以及仿真加载过程名义应力云图Fig.4 Calculated response of KNN model and the nominal stress diagram of simulation loading process

图5 给出了当加载方向平行于纤维方向和加载方向垂直于纤维方向时,利用SVR 模型获得的本构参数的计算响应曲线与利用KNN 模型获得的本构参数的计算响应曲线和实验曲线的比较.从图5 中可以看出,无论加载方向平行于纤维方向还是垂直于纤维方向,利用SVR 模型和KNN 模型预测的骨骼肌本构参数的响应曲线与实验曲线吻合良好.但在加载方向垂直于纤维方向时,利用KNN 模型预测的骨骼肌本构参数的响应曲线比利用SVR 模型与实验曲线吻合更好.

图5 利用SVR 模型获得的本构参数的计算响应与实验数据以及与利用KNN 模型获得的计算响应对比Fig.5 Comparison of calculated response between KNN model and SVR model

图5 利用SVR 模型获得的本构参数的计算响应与实验数据以及与利用KNN 模型获得的计算响应对比(续)Fig.5 Comparison of calculated response between KNN model and SVR model(continued)

为了更直观地观察真实值与预测值的拟合程度,引入了2 种统计指标,包括相关系数(R)和决定系数(R2).R是一个相关性指标,可以用来衡量真实值与预测值之间的关系有多强,R2是一个效率指标如前所述.R为代表预测值的平均值.表1 给出了从统计指标方面比较了利用SVR 模型参数识别方法和利用KNN 模型参数识别方法.

从表1 可以更直观看出,无论是加载方向平行与纤维方向还是垂直于纤维方向,KNN 模型和SVR模型的相关系数R和决定系数R2相差不大,在加载方向垂直于纤维方向时,KNN 模型的相关系数R和决定系数R2比SVR 模型好一些.所以KNN 模型和SVR 模型都是预测本研究中骨骼肌组织的本构参数的准确有效手段.本研究对利用KNN 模型得到的骨骼肌组织的本构参数进行处理,表2 给出了骨骼肌组织本构参数的均值和标准差.

表1 KNN 模型与SVR 模型统计指标比较Table 1 Comparison of statistical indicators between KNN model and SVR model

表2 利用KNN 模型获得的骨骼肌组织本构参数范围Table 2 Range of hyperelastic material parameters of skeletal muscles by KNN model

从表2 可以看出C10在0.508～0.684 kPa 之间,k1在373.361～422.881 kPa 之间,k2在31.235～36.394之间,κ 在0.261～0.299 之间.

4 结论

在本研究中提出了两种有效的反演方法来识别骨骼肌的本构参数.一种是利用K 近邻模型并结合有限元方法来识别骨骼肌的本构参数,另一种是利用支持向量机回归模型并结合有限元方法来识别骨骼肌的本构参数.本研究中的数据集由有限元方法来生成,从骨骼肌组织的单轴压缩实验获得的实验数据用来验证本文提出的反演方法的准确性.最后,用相关系数R和决定系数R2来直观地衡量本文提出的两种模型的准确性,得出如下结论:

(1)本文利用K 近邻模型和SVR 模型确定了可靠的骨骼肌组织的本构参数的范围,所得到的本构参数的计算响应与骨骼肌组织的实验曲线吻合良好.

(2)利用K 近邻模型和SVR 模型在预测骨骼肌组织的本构参数都具有很大的潜力.本文提出的两种模型和有限元相结合的反求方法也可以应用于其他具有超弹性结构的模型的软组织.