一种含惯容和接地刚度的动力吸振器参数优化1)
2021-05-31申永军杨绍普
隋 鹏 申永军,†,2) 杨绍普,†
∗(石家庄铁道大学机械工程学院,石家庄 050043)
†(石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)
引言
动力吸振器(dynamic vibration absorber,DVA)是一种通过附加在主系统上的控制结构吸收主系统的振动能量,降低主振动系统振动的装置.Frahm[1]于1909 年发明了世界上第一种动力吸振器,这种最初的DVA 为无阻尼吸振器,其减振频带有限,亦称为窄带吸振器.Ormondroyd 等[2-3]在无阻尼DVA 中加入阻尼设计出减振效果更好、适用范围更广的Voigt 式DVA,首次提出了固定点理论,并在专著中整理汇总了DVA 最优参数的设计方法.Liu 等[4]设计了一种接地式DVA 并计算了相应的最优参数.申永军等[5-7]设计了多种半主动on-off控制DVA,通过平均法进行了参数优化和控制效果比较,并分析了时滞特性对半主动控制的影响.邢子康等[8]设计出一种新型接地式三要素型动力吸振器,发现系统存在局部最优参数并分析了其性能.李涵等[9]利用H2优化原理对随机激励下的新型滚珠式动力吸振器进行了参数最优设计.白世鹏等[10]研究了布置在不同位置处动力吸振器对车辆垂向振动耗散功率及悬架性能的影响.张卫华等[11]采用牵引电机作为动力吸振器来控制转向架蛇行运动稳定性和蛇行频率,从而避免引起车体弹性模态共振.刘兴天等[12]提出了一种几何非线性摩擦阻尼模型用于分析隔振系统的动力学特性.张婉洁等[13]研究了3 种基于相对速度反馈的含立方刚度的单自由度非线性半主动隔振系统,通过平均法得到了其主共振响应的近似解析解.
负刚度元件因其承载能力大、变形小、可控性好的优点,近年来被广泛应用于系统减振之中.Acar等[14]提出了可以有效降低主系统振幅的含负刚度无阻尼DVA.申永军等[15-18]将负刚度元件接地并应用到多种吸振器之中,证明了含合理负刚度元件的吸振器有着良好的减振性能,特别是文献[18] 发现在放大比和质量比耦合项达到一定值后,最优接地刚度比为正值且系统具有更好的吸振特性.邢昭阳等[19]将放大机构应用于含负刚度弹簧元件的动力吸振器模型,对该模型的最优参数进行了研究.李昊等[20]提出了一种新型准零刚度隔振装置,并对其隔振效果进行了仿真和试验分析.Zhou 等[21]提出了两种含负刚度元件的动力吸振器模型,使用H∞准则和稳定性最大化准则进行了优化.
惯容是一种与两端点加速度相关的新型结构控制元件,在减振控制领域有着较为广泛的应用.Chen等[22]研究了惯容对隔振系统频率的影响.杨晓峰等[23]研究了含惯容的DVA 与主系统的连接方法与耦合关系,提出了车辆ISD 悬架结构设计方法.Hu等[24-25]将惯容应用到隔振、吸振系统中,证明了惯容有着良好的减振隔振特性.Wang 等[26-27]设计了多种含惯容的动力吸振器并推导出其对应的最优参数设计公式.陈杰等[28]提出了两种用于抑制梁振动的含惯容和负刚度动力吸振器模型.Gioacchino 等[29]将菱形支架和惯容组合,提出了一种改进的惯容式动力吸振器.王勇等[30]提出了一种相对加速度-相对速度控制策略调节的半主动惯容器,并将其应用到隔振器中.
惯容可以在基本不改变结构物理质量的前提下改变系统的惯性特征,接地刚度可以调整系统的刚度特性,这两种器件均可改变系统固有频率,进而提高吸振器性能.但目前的大多数研究仅仅是在吸振器中单独引入惯容或接地刚度结构.而随着设备对抑制振动需求的增加,此类吸振器的性能难以满足工程实践需求的增长.少部分同时含有两种元件的吸振器也仅是将惯容接地,相当于增加了子系统质量,并不能体现惯容的两端点惯性特征.本文旨在研究惯容和接地刚度的共同作用对系统稳定性和吸振特性产生的影响,提高吸振器的减振特性.
通过在经典Voigt 型动力吸振器中附加惯容和接地弹簧元件,设计出一种新型动力吸振器模型.利用固定点理论对该模型的刚度和阻尼进行了参数优化,发现惯容和接地刚度共同作用时,惯容存在最佳工作范围.通过与其他类型动力吸振器模型进行对比,证明了含惯容和接地刚度的模型在减振方面有着很大优势,能够极大地降低主系统振幅,同时拓宽了减振频带,为工程实践中设计新型有效的动力吸振器提供参考.
1 动力吸振器模型及参数优化
图1 为本文所提出的动力吸振器模型,其中m1和m2分别表示主系统质量和动力吸振器质量,k1和k2分别表示主系统和吸振器刚度,k3表示接地弹簧刚度系数,c表示吸振器阻尼系数,b表示惯容系数,F0与ω 分别代表激振力的振幅与频率.

图1 含惯容和接地刚度的动力吸振器模型Fig.1 Dynamic vibration absorber model with inerter and grounded stiffness spring
根据牛顿第二定律可得该系统的动力学方程为

1.1 解析解


1.2 最优参数
式(6)经简单推导,可证明其归一化位移幅频曲线通过3 个独立于阻尼比的点,分别为频率比λ=0处的Z点、λ=1 左右两侧的P和Q两点,这3 个点即为本吸振器模型主系统幅频曲线的固定点.为验证本模型的固定点同时便于进行后续优化,现任取阻尼比分别为0.3,0.5 和0.7,绘制归一化位移幅频曲线如图2 所示,从图中可以清楚地观察到曲线均通过Z,P和Q三点.

图2 不同阻尼比下的归一化幅频响应曲线Fig.2 Normalized amplitude frequency response curves under different damping ratios
根据固定点理论,为了使两固定点处纵坐标相等,只需使阻尼比趋于零和无穷时的响应值相等,即

当频率比取最优值时,P和Q两个固定点处响应的纵坐标均为

根据式(18),当质量比µ和惯容比β 为常数时,接地刚度比α 也会影响系统的控制性能,图2 中ω=0 处的Z点也与阻尼比无关.为使幅频曲线的峰值最小,可进一步将3 个固定点P,Q和Z调整到同一高度,于是令

经计算可知,当惯容比取不恰当的值时,上述4个可能的最优解均会引起系统失稳,故推知在动力吸振器的最优设计过程中,在保证系统稳定性的前提下,惯容存在最佳工作范围.现有惯容元件的惯容系数均为正且质量比为正,由式(17)、式(18) 和式(21)表达式易知式中根号下部分均大于0,故现将上述每个刚度比分别代入式(16)中并令其大于0 求解惯容比β,可初步得到每个可能最优刚度比所对应的惯容工作范围.进而将上述求得的刚度比分别代入式(8) 中,在满足各自对应的惯容工作范围内,发现只有α3能保证系统的固有频率均为正值,所以本文模型的最优接地刚度比为α3,即

至此,已经得到了最优频率比与最优接地刚度比,固定点P和Q已经被调整到同一高度.由于P和Q两固定点的坐标与阻尼比ξ 的取值无关,为了达到最优的减振效果,须使两固定点成为位移幅频曲线的最高点或近似最高点.由极值条件可知,幅频曲线在两固定点处的导数为零,即
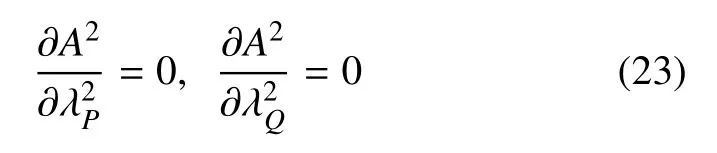
由式(23)可以得到使P和Q两固定点成为或近似成为幅频曲线最高点时ξ1和ξ2的值,进而得到最优阻尼比ξopt=(ξ1+ξ2)/2,但是这种方法有时难以得到解析结果.因此使用文献[4]中的方法求出阻尼比的近似值.
为了使幅频曲线水平通过P点,先假设其通过邻近点P′,P′点的坐标为(λP′,AP′),令

如果δ=0,式(25)为0/0 形式的不定式,于是得到a0=b0=0.由于δ 是一个非常小的量,在式(27)中可以忽略其高次项,此时的阻尼比为

因此只需要找到式(27)的分子与分母中所有δ 的一次项系数

1.3 惯容最佳工作范围
在筛选最优接地刚度比αopt时,已经验证过其满足系统的固有频率大于0.考虑各最优参数及其计算过程,惯容的工作范围应同时满足各表达式分母不等于0,根号下部分大于0,最优频率比vopt和最优阻尼比大于0.
将最优接地刚度比αopt代入最优频率比vopt中可得

2 数值仿真
2.1 数值解与解析解对比
为了验证求解过程的正确性,选取质量比µ=0.1,此时惯容最佳工作范围为(0.454 5,1.909 1),选取惯容比β=0.5,激励幅值F0=1000 N,根据前面的优化结果得到最优参数分别为α=1.302 6,v=0.726 3,ξ=5.391 6.使用四阶龙格库塔法,选取计算时间为500 s,可以得到在给定简谐激励下的数值解.略去瞬态响应,选取稳态解的最大值为响应幅值并进行归一化处理,从而可以得到归一化的幅频曲线.图3 给出了系统的解析解与数值解曲线,黑色实线为系统的解析解,黑色圆圈绘制的曲线为系统的数值解.从图中可以看出,解析解与数值解完全吻合,验证了本文求解过程和各最优参数的正确性,并且证实了最优参数的良好控制效果.

图3 系统解析解与数值解对比Fig.3 Comparison between the analytical solution and numerical solution of the system response
2.2 惯容对主系统响应的影响
2.2.1 最佳工作范围内惯容比对主系统振幅放大因子的影响
选取质量比µ=0.1,此时惯容最佳工作范围为(0.454 5,1.909 1).进一步选取β=0.5,0.8,1.0,1.2,1.5,1.8,相应的系统最优参数值详见表1,并绘制幅频响应曲线如图4.由图4 可知,在惯容最佳工作范围内,惯容比β 越大,主系统归一化位移振幅放大因子越小,两个纵坐标峰值高度越接近,峰值对应的横坐标相隔越远.即惯容系数越大,系统共振区振幅越小,减振频带越宽.由表1 数据可知,在惯容最佳工作范围内,惯容比β 越大,系统最优频率比vopt越大,最优刚度比αopt越大,最优阻尼比ξopt先减小后增大;且越接近惯容最佳范围上限,理论最优频率比和刚度比增大的趋势越大.

表1 惯容比取不同值时系统各最优参数取值Table 1 Specific parameters of the system in different cases of inerter-to-mass ratio

图4 惯容比对归一化位移振幅放大因子的影响Fig.4 Comparison of the normalized amplitude magnification factors of the primary systems for different inerter-to-mass ratios
2.2.2 最佳工作范围外惯容比对主系统振幅放大因子的影响
当惯容比取值为最佳工作范围外的值时,使用前面的优化结果会得到不合理的最优值,如负的频率、阻尼等,因此这些优化结果便不再适用.在工程实践中,如因某些不可避免的因素导致惯容系数无法取最优范围内的数值,可采取折中的设计.当惯容比小于最佳工作范围时,可按照惯容比略大于下限时对应的最优参数进行吸振器的设计和使用.例如当质量比为µ=0.1 而惯容比分别为β=0.1,0.2,0.3,0.4 时,均取略大于最佳范围下限的值β=0.454 6.此时对应的最优设计参数为α=1.200 1,v=0.024 4,ξ=144.351 2.激励幅值取F0=1000 N,在Matlab 软件中进行仿真模拟,得到图5.由图5 可以观察到,如此设计吸振器,仍具有良好的减振效果.

图5 惯容比小于最佳范围下限时主系统响应情况Fig.5 Response of primary systems when the inerter-to-mass ratio is less than the lower limit of the optimal range
当惯容比大于最佳工作范围时,质量比µ=0.1,略小于最佳范围上限的惯容比值β=1.909 0,对应的理想最优设计参数为α=46 198.476 2,v=648.048 0,ξ=3.015 1.显然此时接地弹簧刚度系数过大,在实际应用中难以实现,故应尽量避免惯容系数取值过大的情况.
3 与其他动力吸振器模型对比
为验证本文提出的动力吸振器模型的减振效果,将该模型(后文称之为IG-Voigt 模型) 与经典Voigt型动力吸振器、接地型动力吸振器[2-4]及文献[13]中附加负刚度元件的Voigt 型动力吸振器(后文称之为N-Voigt 模型)进行了对比,3 种对比吸振器模型如图6 所示,各模型对应的最优参数公式详见表2.

图6 现有动力吸振器模型Fig.6 Existing models of dynamic vibration absorbers
3.1 简谐激励下的响应对比
工程中很多设备尤其是旋转机械经常受到简谐激励,因此首先比较不同激励频率下各模型的减振效果.各模型均取质量比µ=0.1,本文模型惯容比取β=0.5,并按照前面推出和表2 中已有的最优参数设计公式,计算相关参数,仿真不同频率简谐激励下主系统的位移响应,得到各模型归一化位移幅频曲线如图7 所示.

表2 吸振器模型参数最优设计公式Table 2 Optimal design formula for model parameters of DVAs

图7 与其他形式吸振器模型对比Fig.7 Comparison with other DVA models
从图7 中可以看出,在质量比相同的情况下,本文模型相对于其他类型的动力吸振器可大幅降低主系统振幅,并且产生的两个共振峰值的间距更大,峰谷也更低,从而同时拓宽了减振频带.
3.2 随机激励下的响应对比
在土木和建筑工程中系统所受的激励多为随机激励,因此本文进一步研究了宽频随机噪声激励下的主系统响应情况.设主系统受到均值为零、功率谱密度为S(ω)=S0的白噪声激励,则前述4 种模型主系统位移响应的功率谱密度函数分别为

其中下标V,R,N,IG 分别代表Voigt 式动力吸振器模型、接地型动力吸振器模型、N-Voigt 型动力吸振器模型以及本文模型.这4 种动力吸振器模型的主系统位移均方值为

假设4 种动力吸振器中质量比均取µ=0.1,本模型惯容比取β=0.5,根据相应优化公式得到各自的均方值分别为

结果表明,当初始参数相同时,在随机激励情况下本文模型仍具有良好的减振效果.
为了更真实地模拟工程实际,本文构建了50 s均值为0、方差为1 的随机激励,其时间历程如图8 所示.由于系统振动能量可由主系统位移方差衡量,选取主系统质量m1=1 kg,主系统刚度k1=100 N/m,在表3 中总结了主系统位移方差及其衰减比.

图8 随机激励时间历程Fig.8 Time history of the random excitation
由表3 可以看出,虽然已有模型和本文模型都是依据H∞优化准则进行设计的,但是本文模型仍然能够在整个频率范围内大幅降低主系统的振动能量,比其他3 种模型具有更良好的减振性能.

表3 主系统响应方差及其衰减比Table 3 Variances and decrease ratios of the displacements of the primary systems
4 结论
提出了一种含惯容和接地刚度的动力吸振器模型,对该模型进行了参数优化,得到了最优频率比、最优刚度比和近似最优阻尼比.发现惯容和接地刚度共同作用时,在最优设计过程中,不恰当的惯容系数会使系统出现失稳现象,由此得到了惯容的最佳工作范围.分析了惯容比取其最佳工作范围内外值时吸振器的减振效果,为实际生产中设计新型吸振器提供参考.通过与其它类型的动力吸振器对比,说明了合理惯容和接地刚度的引入能够大幅降低主系统振幅,拓宽减振频率,带来良好的减振效果.
