层状分数阶黏弹性饱和地基与梁共同作用的时效研究1)

2021-05-31艾智勇慕金晶

力学学报 2021年5期

艾智勇王禾慕金晶

(同济大学地下建筑与工程系,岩土及地下工程教育部重点实验室,上海 200092)

引言

弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用,并因为简单适用而备受青睐.国内外很多学者针对弹性地基梁问题开展过研究工作[1-9],但这些研究多基于弹性地基或Winkler 地基模型.当基础置于饱和地基时,土体同时存在固结和蠕变变形,故需要考虑地基与基础相互作用的时效性.许多学者对饱和地基的固结问题进行过深入研究,一般将地基视为饱和弹性介质[10-16]或饱和黏弹性介质[17-18].Gemant[19]通过试验发现,经典的整数阶微分流变模型存在一定局限性,建议采用基于分数阶导数的微分流变模型.近年来,不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20-24].解益等[25]、汪磊等[26]将分数阶导数理论引入Kelvin–Voigt 模型,给出了黏弹性饱和土体一维固结问题的半解析解法.基于Merchant 流变模型,时刚等[27]研究发现:分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异.刘忠玉等[28]引入Koeller 定义的弹壶元件以建立分数阶Merchant 模型,然后对考虑非达西渗流的饱和土体流变固结机制进行了分析.借助分数阶Kelvin 本构模型,王珏等[29]研究了循环载荷作用下黏土地基的一维固结沉降特征.吴奎等[30]采用Abel 黏壶替代牛顿黏壶,基于改进的分数阶Burger 模型研究了高地应力深埋软岩的流变问题.已有的研究表明[20-23],分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为.

基于饱和黏弹性地基的固结解,Ai 和Hu[31]利用有限元-解析层元耦合法研究了层状饱和地基与梁的共同作用问题,并考虑了地基的渗透各向异性和孔隙流体的可压缩性.Kobayashi 和Sonoda[32]基于Winkler 地基假定,借助弹性-黏弹性对应原理,给出了多种线性黏弹性地基上Timoshenko 梁弯曲问题的解答.苏超等[33]也利用弹性-黏弹性对应原理,建立了黏弹性地基上基础梁的计算方法,并将其应用于软土地基上船闸底板的计算.Bhattiprolu 等[34]提出了非线性黏弹性地基上弹性梁的有效求解方法,且该方法能够处理二者间接触区域非连续的情况.Sreekantan 和Basudhar[35]基于Burger 模型对黏弹性地基上梁的受弯响应进行了分析.目前针对黏弹性地基上梁的研究中,很少考虑到分数阶黏弹性以及地基的成层特点.因此,开展层状分数阶黏弹性饱和地基与梁的共同作用研究具有重要的理论意义和工程应用价值.

本文采用有限元法对Timoshenko 梁进行分析,采用边界元法对地基进行分析,将文献[36] 中分数阶黏弹性饱和地基的固结解答作为地基边界积分方程的核函数,建立梁节点沉降与地基反力间的柔度矩阵方程;然后根据梁与地基接触面上的位移协调条件和力的平衡条件,推导出层状黏弹性饱和地基与Timoshenko 梁共同作用的解答;最后探讨分数阶次和地基成层性对梁与饱和黏弹性地基共同作用的影响.

1 Timoshenko 梁的有限元分析

如图1 所示,Timoshenko 梁置于一层状黏弹性饱和地基上,并在外载荷和地基反力的共同作用下处于平衡状态.

图1 Timoshenko 梁受力示意图Fig.1 Force diagram of a Timoshenko beam

已知的外载荷可以是分布载荷p(x)、集中载荷Pi或集中力偶Mj.梁的总长度为L,以k个节点将其等分为(k-1) 个梁单元,每个梁单元的长度为l=L/(k-1).为使地基反力R(x)对应的单元个数与梁节点数量相同,将梁与地基的接触面划分为k个单元,并假设各单元分别受到大小为Ri(i=1,2,···,k)的均布反力.其中,R1和Rk所在的接触面单元长度为l/2,其他接触面单元长度均为l.本文假定各梁单元底部的地基反力为均布力,这与实际情况有所不同.因此,需要通过选取合适的单元数目,将地基反力的计算误差控制在可接受范围内.

取任意梁单元进行分析,单元节点的载荷分量和位移分量如图2 所示.M和Q分别为截面上的弯矩和横向剪力,w和θ 分别为梁的挠度和截面转角,角标1 和2 用以指示载荷及位移分量所在截面.

图2 梁单元示意图Fig.2 Sketch of a beam element

基于Timoshenko 梁理论,可得梁单元的有限元求解方程[37]

2 Timoshenko 梁与地基共同作用方程

如图3 所示,采用分数阶Merchant 模型描述黏弹性地基的本构关系,该模型由线弹性体和Kelvin 体串联而成,E0和E1分别为线弹性体和Kelvin 体的弹性模量,η 为黏滞系数,α 为分数阶次.不同的分数阶次可以表征不同的蠕变状态,从而有效模拟饱和地基的流变特征.其对应本构方程如下

图3 分数阶Merchant 模型Fig.3 Fractional Merchant model

层状正交各向异性黏弹性饱和地基上的Timoshenko 梁见图4.梁截面的宽度和高度分别为bb和hb,梁端自由,其与地基的接触面光滑,且二者在加载后紧密接触.黏弹性饱和土体正交各向异性参数ζ=E0h/E0v=E1h/E1v=ηh/ηv,下标h和v分别表示水平向和竖向参数;vh为水平应力引起正交水平向应变的泊松比,vvh为竖向应力引起水平向应变的泊松比;kh和kv分别为水平向和竖向渗透系数.

图4 层状正交各向异性黏弹性饱和地基上的Timoshenko 梁Fig.4 Timoshenko beam on the layered cross-anisotropic viscoelastic saturated soils

文献[36]利用弹性-黏弹性对应原理对层状正交各向异性黏弹性饱和地基的固结问题进行了求解,但该解答仅针对地基上作用骤加载荷的情况.实际上,由于孔隙水的存在,梁与饱和地基的相互作用过程中,地基反力和沉降会随时间缓慢变化.这时任意地基单元i在t时刻受到的作用力有如下积分型表达[31]

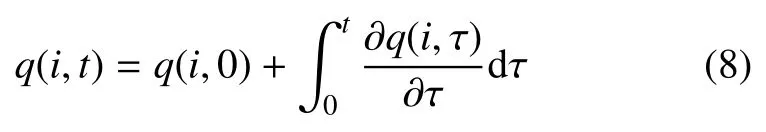
式中,q(i,0)和q(i,t)分别表示0 时刻和t时刻作用在梁单元i上的作用力.

因此,t时刻由i梁单元下的地基表面受到的作用力引起的j节点处地基表面的位移可表示为

式中,Is(j,i,t) 为在第i个地基单元表面作用单位均布载荷,经过t时间段时,在梁节点j下地基表面处产生的竖向位移,其可根据地基固结解[36]求得.

对于形如式(9)的方程,可采用卷积公式进行化简.卷积公式的定义如下[38]

式(10)在Laplace 变换域内具有如下性质

对式(9)进行Laplace 变换,并结合该性质,可以得到Laplace 变换域内s时刻地基单元i处作用的缓变载荷与梁节点j下地基表面竖向位移之间的关系

式中,为Laplace 变换域内的柔度系数.

梁节点j下地基表面的总竖向位移由所有地基单元表面所受的作用力共同作用产生,故将式(12)应用于所有地基单元,可得Laplace 变换域内地基表面位移和地表作用力之间的关系如下

至此,已经分别建立了Laplace 变换域内梁的总刚度矩阵方程和地基的柔度矩阵方程.利用梁-土接触面间的协调条件,可以将梁与地基联系起来.假定外载荷作用下地基与梁底面紧密接触,则梁节点的竖向位移与对应位置的地基沉降相等,而地基反力与基础对地基的作用力大小相等,即

结合式(15),并将地基柔度矩阵方程式(13)代入梁的总刚度矩阵方程式(4)中,可得到梁与地基共同作用的总矩阵方程

求解该式即可得出Laplace 变换域内梁各节点转角和单元底部的地基反力,地基沉降可通过式(13)进一步获得.对以上解答进行Laplace 数值逆变换[31],即可得到各分量在物理域内的真实解.

3 数值计算与分析

3.1 验证

Kobayashi 和Sonoda[32]针对多种线性黏弹性地基上Timoshenko 梁的弯曲问题进行了研究,其中基于Kelvin 地基模型的相关研究可视为本文模型的特例.为此将本文模型退化至Kelvin 地基,并与文献[32] 中的算例进行对比.算例中均布载荷p作用于梁中部0.4L≤x≤0.6L区域,弹性梁与黏弹性地基的相关参数满足:其中,ks为地基基床系数,需借助Vesic[39]给出的理论公式将其换算为弹性模量.

图5 和图6 分别为梁中点处地基沉降和地基反力随时间的变化曲线.由图可见,本文理论退化至Kelvin 地基后所得解答与文献[32]结果吻合良好,具有很好的一致性.

图5 Timoshenko 梁中点处地基沉降随时间的变化Fig.5 Settlement at the midpoint of the Timoshenko beam with time

图6 Timoshenko 梁中点处地基反力随时间的变化Fig.6 Subgrade reaction at the midpoint of the Timoshenko beam with time

3.2 单元数目的影响分析

为便于分析,本文将对梁与地基的部分参数及固结计算结果进行无量纲化处理.无量纲位移w∗、地基反力R∗及时间参数τ 的具体定义见各图中标注,其中µ=(1-vvh)/[2(1+vvh)(1-2vvh)].梁-土相对刚度比定义为

Timoshenko 梁置于均质黏弹性饱和半空间地基上,其上表面在全长范围内作用竖向均布载荷p.梁的参数为:长高比L/hb=6,截面宽高比bb/hb=1,泊松比νb=0.15;地基土的相关参数为:E0v=10 MPa,E1v=5 MPa,ηv=1.0×106MPa·s,ζ=1,νvh=νh=0.35,kv=kh=5.0 × 10-8m/s;梁-土相对刚度比Kb为0.1.本文取分数阶次α=0.4,0.6,0.8,1.0 进行对比分析.

本节探讨梁单元数目对计算结果的影响.当梁节点数目k=3,7,11,17,21 时,计算得到的固结完成时(τ=1012)梁与地基接触面的沉降见图7.

图7 单元数目对地基沉降的影响Fig.7 Effects of the number of elements on settlements

由图7 可见,当梁节点数目k≥7,即梁单元数目大于等于6 时,梁单元数目的增加对梁与地基相互作用的计算结果影响已不再显著.显然,随着单元数目的增加,数值解答的精度随之提高,但计算效率也在逐渐下降.考虑到计算效率和精度的平衡,本文算例均取k=11,即将梁划分为10 个单元,此时所得结果的误差在可接受的范围内.

3.3 分数阶次的影响分析

对于实际工程中模型分数阶次等参数的取值问题,可参考文献[20,22-23] 中的试验方法.具体为:取工程所在区域的土样进行三轴流变试验,得到土体蠕变曲线;然后依据本构关系式,通过曲线拟合方法得到与蠕变曲线相吻合的分数阶黏弹性模型参数.另外,所取蠕变曲线对应的加载条件应尽量与实际工程的工况条件一致,以保证能有效反映实际工程条件下该区域土体独特的流变特性.

基于3.2 节中的梁和地基参数,可计算得到如图8 和图9 所示的不同分数阶次下梁中心地基沉降和梁端地基反力随时间的变化情况.由于土体固结及蠕变变形的存在,梁下地基沉降及地基反力表现出明显的时变特征.例如,地基沉降及地基反力的时变曲线在固结初期较为平缓,而后有比较明显的增长,最终随时间发展而趋于某一定值.另外,分数阶次α 对梁底地基沉降和地基反力均有较大影响.当其他参数不变时,饱和地基固结速率随α 的增大而明显加快,梁底地基沉降量及端部地基反力都会更早达到最终值;但不同分数阶次下,梁中点处地基的最终沉降以及端部的最终反力相同.

图8 不同分数阶次下梁中点地基沉降随时间的变化Fig.8 Settlements versus time at the midpoint of the beam with different fractional orders

图9 不同分数阶次下梁端部地基反力随时间的变化Fig.9 Subgrade reactions versus time at the end of the beam with different fractional orders

实际上,分数阶次α 的取值决定了分数阶Merchant 模型(见图3)中Abel 黏壶的物理性质:当α=0时,该元件为线弹性固体;当α=1 时,为理想牛顿流体;当0 <α <1 时,为分数阶黏弹性体.Yin 等[22]经研究指出,随着分数阶次α 的增大,土体孔隙水压力消散得更快,故达到最终沉降所需时间更短.另外,当孔隙水压力完全消散,不同分数阶次模型下的土体均达到最终沉降状态,此时各梁-土接触面上的地基沉降及反力也达到相同状态.解益等[25]曾将分数阶Kelvin 模型下黏弹性饱和土体的固结沉降表达式退化至整数阶黏弹性模型以及弹性模型,从理论上证明了不同分数阶次下土体最终沉降量相同.

3.4 地基成层性的影响分析

本节将探究地基成层性对梁土相互作用的影响.3 种饱和土体的相关参数见表1,3 种分层工况见表2.土体1 和土体2 为黏弹性饱和土,土体3 为弹性饱和土.E∗表示终态模量(1/E∗=1/E0+1/E1),其值一定程度上能反映土体的整体压缩变形性能.地基总厚度为H=10L,自上而下三层土体的厚度比例为h1:h2:h3=1 :1 :8;弹性梁参数同3.2 节,梁上作用竖向均布载荷p.为便于分析,计算无量纲时间和无量纲竖向位移时,统一将E1v取为E∗=5 MPa.

表1 3 种饱和土体的参数Table 1 Parameters of three different saturated soils

表2 3 种层状地基工况Table 1 Three cases of different multilayered soils

由图10 和图11 可见,工况1 中均质单层地基的弹性模量较小,因而弹性梁底的地基沉降比其他两种工况更大.与工况1 相比,工况2 中首层土的性质相同,下部土体较硬,梁下地基沉降量较工况1 有一定程度的减小.而工况3 中的首层土弹性模量较大,相比工况1 和工况2,可有效控制地基沉降.

图10 地基成层性对地基沉降的影响(τ=106)Fig.10 Effects of the stratification of soils on settlements(τ=106)

图11 不同层状地基下梁中点地基沉降随时间的变化Fig.11 Settlements versus time at the midpoint of the beam with different multilayered soils

图12 中的Δw为梁中点及端部地基沉降量之差,Δw∗为其无量纲化后的值.工况2 和工况3 下的沉降差曲线很相近,而工况3 对应曲线的沉降差值明显降低.这说明加固表层土体不仅对控制地基的整体沉降有显著效果,也能大幅减小地基的差异沉降.实际上,由于梁受荷造成的地基附加应力的影响深度有限,且附加应力随深度的增大而明显减小,故加固表层土体能够对地基沉降起到明显的控制作用.