结构参数化建模在大跨空间钢结构中的应用
2021-05-31
(成都基准方中建筑设计有限公司,成都 610000)
引言
随着建筑参数化设计方法的流行,有着复杂曲面表皮的建筑犹如雨后春笋拔地而起。这些建筑造型优美,充满了流动感和韵律感。同时由于建筑曲面复杂,也给结构设计工作带来了难度。空间复杂曲面结构的建模十分繁琐[1-2],项目方案初期,建筑师对建筑表皮曲面进行频繁调整和修改,对于采用传统结构建模方法,一旦建筑表皮曲面改动,结构模型也将重新进行结构找形和建模,工作量成倍增加。
结构参数化建模能够很好地解决这一问题。结构参数化建模可以让结构构件与建筑表皮联动,建筑表皮调整,结构构件自动调整,无需要重新找形或建模。不仅如此,结构参数化建模可以将一些结构形态参数(如桁架高度、网格大小、建筑表皮与结构构件中心线的距离等)进行参数化,通过这些参数实时调整结构模型。
本文基于Rhino+Grasshopper参数化建模平台介绍了网架、网壳和管桁架等常用空间结构的参数化建模,并结合多个工程实例,重点介绍了大跨空间钢结构参数化建模。
1 参数化建模简介
1.1 参数化平台简介
目前,结构参数化设计的软件平台可分为两大类,一类是基于有限元软件的设计平台,如ANSYS 的APDL,其特点是结构分析能力强大,但建模能力有限,适用于几何拓扑较为简单的工程(如平板网架)。二类是建模造形专业软件,这些软件往往自带参数化建模模块或二次开发插件,如Rhino+Grasshopper、Catia+DP等,该类软件建模能力强大,能快速建立各种复杂曲面,但自身无结构计算能力,需要依赖于二次开发的插件或外部计算程序,适合几何拓扑复杂的工程[3]。
Grasshopper是基于Rhino平台开发的可视化编程语言。“可视化编程”的优点是上手容易,无需了解程序编写语法和语句,设计人员可以利用软件本身提供的各种控件,像搭积木一样的构建程序,极大提高了没有计算机程序编制能力的结构设计人员的工作效率。“节点式”是指将各种程序命令封装成节点,通过各节点间的关联操作得到具有一定功能的程序,这种节点式的编程方式强调了节点之间的数据关联,使结构设计人员很清晰地掌握对复杂结构各杆件之间的相互关系[3-4]。
本文案例均采用Rhino+Grasshopper平台进行参数化设计。
1.2 参数化建模
网架、网壳以及管桁架都是常用的空间结构,为此分别编写Grasshopper网架生成程序[5]、Grasshopper网壳生成程序、Grasshopper管桁架生成程序。
三个Grasshopper程序主要功能有:(1)通过建筑外皮自动生成网架、网壳和管桁架; (2)可调整建筑外皮到结构构件距离; (3)可调整网格的横向、纵向尺寸以及结构高度。
图1为一个任意的建筑曲面,分别采用网架生成程序和网壳生成程序,得到该建筑表皮对应的网架(图2)和网壳(图3)。

图1 建筑表皮

图2 Grasshopper生成的网架结构及程序思路

图3 Grasshopper生成的网壳结构及程序思路
其中,网架和网壳生成程序只需给出建筑表皮,即可完成结构生成。管桁架生成程序(如图4-5所示)除需要给出建筑表皮外,还需要调整建筑表皮到结构线距离、桁架宽度、单元格长度、桁架高度等参数,这些参数可以通过数值电池很方便地进行实时调整,如图6所示。同时需要设计人员根据柱子位置等条件给出桁架的水平位置,如图7所示。这样做的目的是:在工程中由于桁架的布置一般是由柱位等条件因素决定的,而并不是均匀布置,不同的工程,管桁架的布置差别很大,所以需要设计人根据具体工程条件给出桁架的布置方式。

图4 Grasshopper生成的管桁架及程序思路

图5 Grasshopper管桁架生成程序

图6 Grasshopper管桁架生成程序的调节参数

图7 管桁架生成时要求给出的条件
1.3 结构参数化计算与优化探讨
(1)带有结构构件信息的参数化模型
在结构设计中,不仅需要建立杆件线模型,还需要进一步完善计算模型,在杆件中加入材料信息、截面形状及截面方向等信息。Grasshopper中的插件GeomgymIFC,能实现赋予截面属性、指定杆件截面等一些结构操作,并将这些信息存储在参数化模型中[6]。同时,该插件能将参数化模型转化为IFC格式,从而达到与结构计算软件(如SPA2000、Midas等)无缝对接,实现从参数化结构建模到结构计算的快速转换。特别是在多个不同的结构方案比选中,省去了多次重复赋予截面属性等操作,大大提高了前期方案试算比选工作的效率[7]。
(2)参数化计算
空间结构的传统设计中,一般是先建立线模型(常规方法或参数化方法),再将该线模型导入到计算软件中(如SPA2000、Midas等),再进行计算设计[8]。
Grasshopper中的有限元计算插件能直接在Grasshopper平台中完成结构的计算,省去了中间模型的转化。当对参数化模型中参数进行调整时,计算结果实时更新。表1罗列了常见的有限元计算插件,虽然这三款软件均能进行有限元计算(内力位移、应力应变),但只有ParaStaad能按照规范进行截面验算。另外两个插件Millipede和Karamba,可以通过二次开发编写对应的截面验算插件。
这些软件均采用有限元算法,对力学问题求解,计算结果(弹性计算)准确性满足工业要求。同时综上所述,这些插件由于在Grasshopper平台中完成计算,省去了导入计算软件、添加截面材料、边界条件、荷载等重复建模工作,大大提高了工作效率。同时,参数化计算能做到了实时修改模型,在Grasshopper中实时显示更新结果。

表1 部分关键词点度中心度数据
(3)结构参数化优化
把上述有限元计算插件与优化算法进行结合,优化算法根据有限元计算插件的计算结果,自动调整模型参数,通过不断迭代得到最优解,这一过程称为结构参数化。常用的结构参数化优化有形态优化、结构构件布置优化和拓扑优化等[9]。
形态优化:如图8所示,结构在最初形态为三角形,在竖向均布荷载作用下,结构形态优化为拱形。通过上述优化可知,在竖向均布荷载下结构的最优形态为拱形。

图8 竖向均布荷载下结构形态优化
结构构件布置的优化:如图9、图10所示,通过结构优化算法对该桥的拉索布置进行优化,得到较优的结构布置方案。

图9 优化前的桥索布置

图10 优化后的桥索布置
拓扑优化:在结构中去除利用率低的部分,以达到轻质高强、节约材料的目的。如图11所示,采用拓扑优化得到最优的材料分布,再采用杆件代替,可以得到较优的桁架杆件布置方案[10]。

图11 悬臂梁在竖向荷载作用下的拓扑优化
2 某会展中心大跨空间结构参数化建模
2.1 工程概况
某国际会展中心项目位于贵阳市。地上一层,采用大跨度空间钢结构体系,屋盖最高点32m,平均高度约23m,长159m,宽89m,屋盖投影面积9450m2。主要功能为展览空间,夹层功能为办公及设备机房。地下二层,主要功能为车库和设备机房。

图12 会展中心三维效果图
本结构为刚架结构(也可视为单层网壳),结构体系较为清晰:
(1)主结构:由29榀径向钢架和1根螺旋环向主梁组成,如图13所示。其中每榀径向钢架由树杈柱与钢梁组成,如图14所示。
次结构:由46榀径向钢架、环向次梁组成以及斜撑组成,如图15所示。
中间采光顶,如图16所示。

图13 主结构(29榀径向钢架+1根螺旋环)

图14 典型径向刚架截面
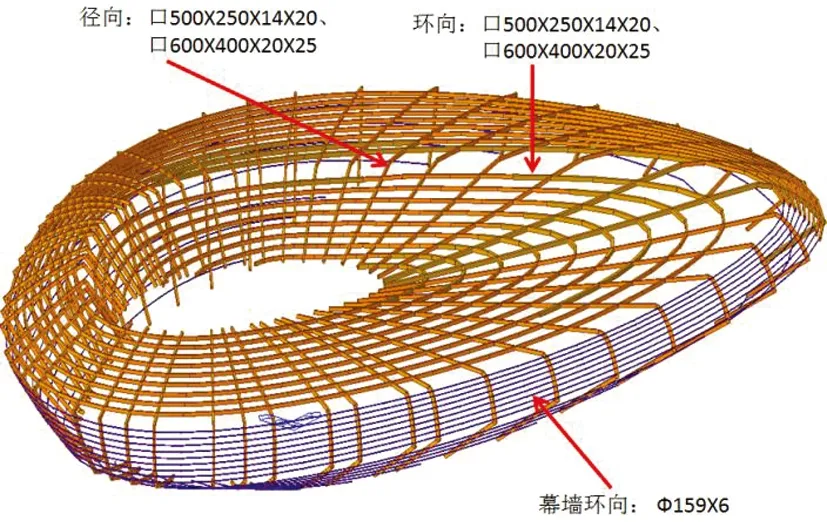
图15 次结构(46榀径向钢架+螺旋环+斜撑)
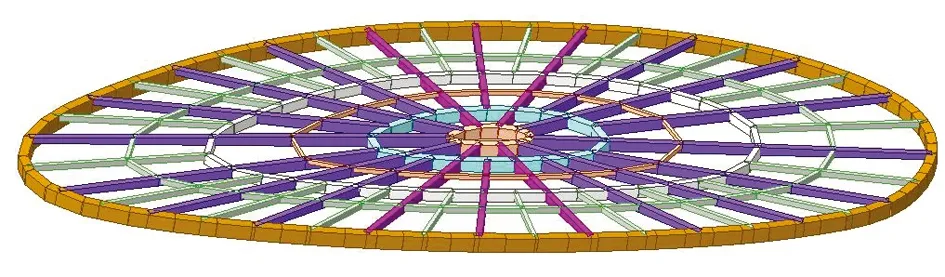
图16 中间采光顶
2.2 结构参数化建模
可以看出,主要屋面结构线由径向划分线和环向划分线组成。生成结构线通常采用如下策略:由建筑表皮偏移得到结构表皮,再通过切割线对结构表皮进行径向划分得到径向结构线,再由曲面直接生成环向结构线(也可采用环向划分得到),如图17所示。

图17 结构线生成策略一
但在本工程中,建筑表皮曲面为复合曲面,偏移之后会丢失一些曲面特征,无法进行精确的找形建模工作。鉴于以上原因,本工程采用另一种结构线生成策略:先对建筑表皮进行切割生成建筑表皮的径向划分线、环向划分线以及结点(径向线与环向线的交点),再对径向划分线和结点进行平面内偏移得到结构径向线和结点,再由结点连接环向线,如图18所示。

图18 结构线生成策略二
程序主要分为四个模块:生成建筑表皮划分线程序、生成结构线程序、生成天窗结构线程序、生成幕墙体系程序。
生成建筑表皮划分线程序:通过切割线对建筑表皮进行径向划分得到径向表皮划分线,再由曲面直接生成环向表皮线。
对建筑表皮径向划分线进行竖向平面内偏移得到结构径向线和结点,再由结点连接环向线,得到结构线,如图19-20所示。在该模块中将建筑表皮径向划分线到结构径向线的偏移距离参数化,方便以后随时调整,如图21所示。该距离为结构专业预留给幕墙专业的结构高度。

图19 生成结构线流程

图20 单榀建筑表皮径向线内偏成结构径向线示意图(平面内偏移)

图21 对建筑表皮到结构表皮的距离进行参数化
生成天窗结构线程序:由于建筑专业已经将窗格线画出,只需将窗格线下偏就可得到天窗结构线。再生成结构天窗外圈梁及与吊杆(吊杆连接主结构环梁和天窗外圈梁),如图22所示。在该模块中将玻璃顶到下方结构的距离参数化,将外圈水沟的结构预留距离参数化。
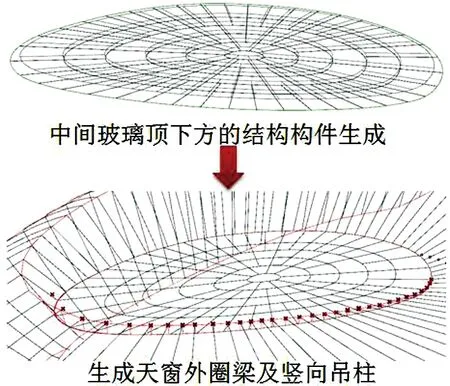
图22 对建筑表皮到结构线的距离进行参数化
生成幕墙体系程序,如图23所示。
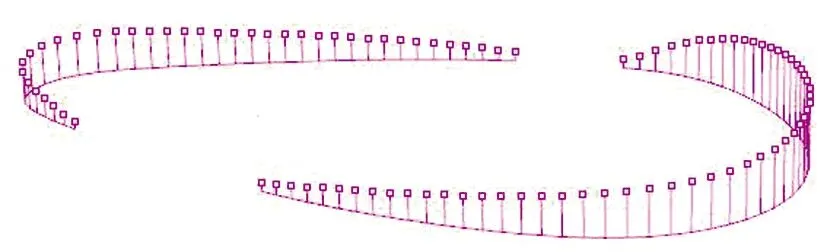
图23 生成幕墙结构线
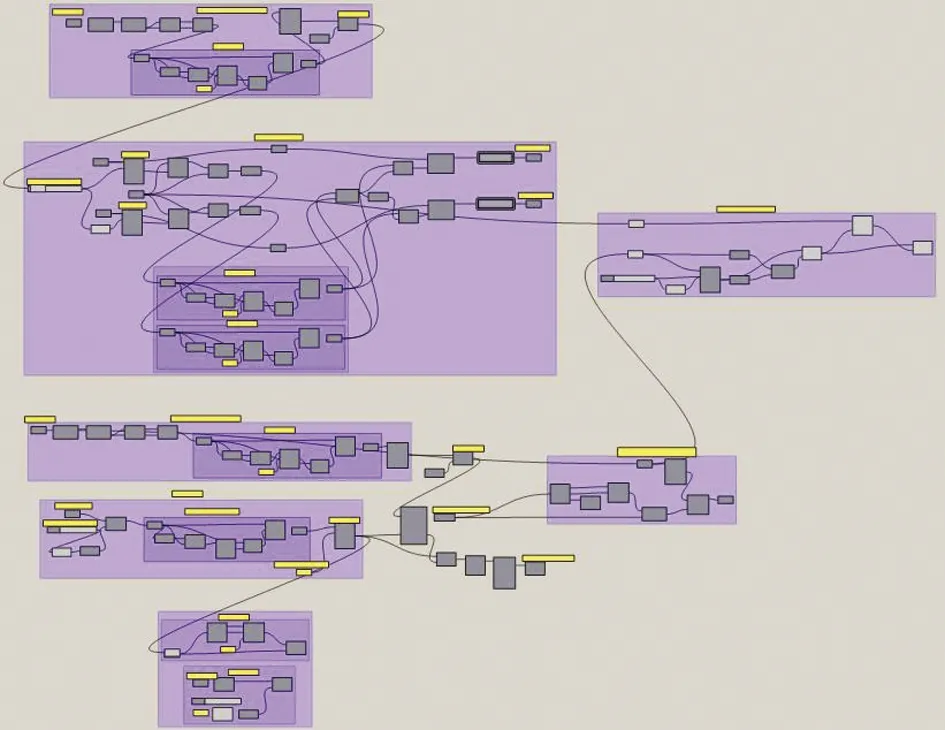
图24 会展中心Grasshopper程序
通过以上多个Grasshopper建模程序(图24),能快速生成该项目结构用线模型,通过参数化设置,可以快速调整模型相关参数,如建筑表皮到结构表皮的距离、主结构划分间距等参数。同时,当建筑调整建筑表皮时,结构可以快速地重新生成相应的结构线模,避免建筑修改带来巨大的结构修改量。
2.3 结构计算
将已建立好的模型导入到Midas GEN进行结构计算与设计,最大应力比为0.88,最大在标准组合下(D+L),结构最大竖向变形为205mm,按相应悬挑跨度41.9m计算,扰跨比为1/204,满足规范1/200要求。通过以上计算,该项目满足承载力及正常使用极限状态要求。
为验算结构的整体稳定性,将参数化模型导入到ABAQUS进行非线性屈曲分析(几何非线性、材料非线性),采用整体屈曲模态(第一阶)为初始缺陷,缺陷最大位移值为最大跨度的1/300。计算结果表明,全跨工况下计算得到一阶屈曲值为2.75(D+L)>2.0(D+L),满足规范要求。半跨活载工况LPF-位移曲线均在全跨工况LPF-位移曲线上,表明一阶屈曲值均大于2.75(D+L),满足规范要求,见图25。因此结构满足整体稳定性要求。

图25 位移-LPF曲线
3 某中小学体育馆及音乐厅结构参数化建模
3.1 工程概况
某学校位于四川省德阳市,总建筑面积为17.2万m2,其中小学初中部约7.6万m2,高中部约9.6万m2,中小学由教学楼、行政楼、宿舍、食堂、风雨操场、教学配套用房等组成。
其中中小学体育馆、高中体育馆及音乐厅屋盖采用空间大跨钢结构。中小学体育馆建筑面积约为6 982m2,屋面投影面积约为2 010mm2,建筑高度为19.7m。高中体育馆建筑面积约为7 761m2,屋面投影面积均为2 579mm2,建筑高度为22.705m。音乐厅建筑面积约为9 369m2,屋面投影面积均约2 410mm2,建筑高度为23.8m。
3.2 结构参数化建模
高中体育馆、中小学体育馆及音乐厅屋盖采用平面钢桁架,屋盖以下部分采用钢框架结构。由于该三栋楼结构形式及布置一样,只是纵向柱距(X向)、横向跨度(Y向)、各层层高、坡屋面长宽、坡屋面檐口高度及屋顶高度等参数不同,如图26所示。相比传统建模方法,参数化建模方法对于这种多栋相似的情况有较大优势,只需建立单个模型,并将不同的模型参数设置为参数化模型中的变量(表2),通过修改这些变量,就可以得到其它的楼栋模型。对于该项目首先建立高中体育馆的参数化模型,设置参数化模型变量,通过修改这些变量,可以很快得到中小学体育馆和音乐厅的模型。充分发挥了参数化模型一次建模一劳永逸的特点。
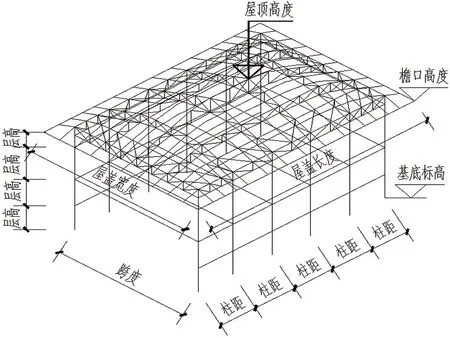
图26 体育馆及音乐厅结构模型参数示意

表2 体育馆及音乐厅结构模型参数

图27 钢屋盖(主次桁架部分)模型参数示意
桁架布置采用柏式桁架,由于建筑外观和功能需要桁架下弦设置为拱形。同样采用参数化方法将下列参数设置成模型变量:1)上弦中线到建筑面层距离(屋面做法预留); 2)主桁架两边高度; 3)主桁架中间高度; 4)横向主桁架划分数; 5)纵向次桁架划分数。通过调整上述各参数,满足建筑处观和功能要求,同时可以进行不同参数的模型试算工作,找到受力较优的结构布置方案。三个楼栋钢屋盖主次桁架的具体参数表3所示。

图28 主桁架参数示意
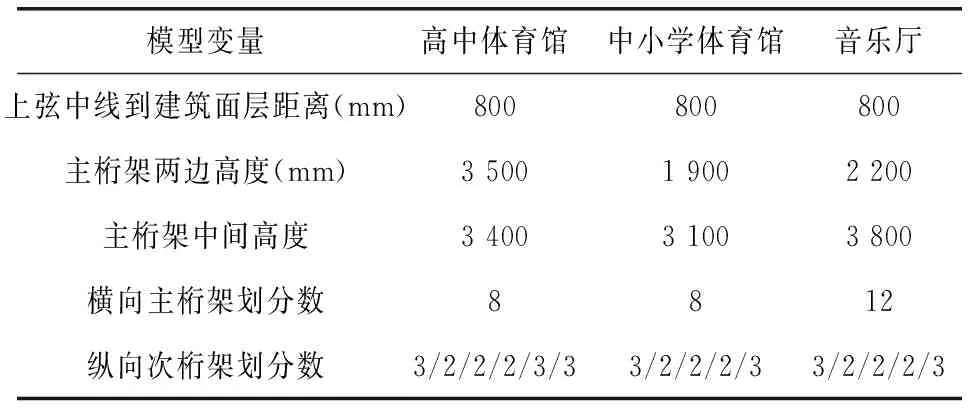
表3 钢屋盖(主次桁架部分)模型参数
通过以上介绍可以看出,由于高中体育馆、中小学体充馆以及音乐厅,均采用相同的屋盖结构形式,它们之间的差别仅体现在层高、屋盖尺寸、檐口高度等方面,采用参数化建模将这些参数设成程序变量,通过调整参数,能快速地生成三个楼栋的结构线模型,大大加快了建模速度。
3.3 结构计算
通过以上建立的参数化线模,将该模型导入到 Midas Gen中进行计算,结构最大应力比分别为0.812、0.816和0.75,如表4所示。

表4 最大应力比(强度和稳定性)
标准组合工况D+L下主桁架跨中最大竖向扰度分别为1/788、1/782、1/698。X向和Y向层间位移有均小于1/250,如表5所示。综上,结构满足刚度要求。
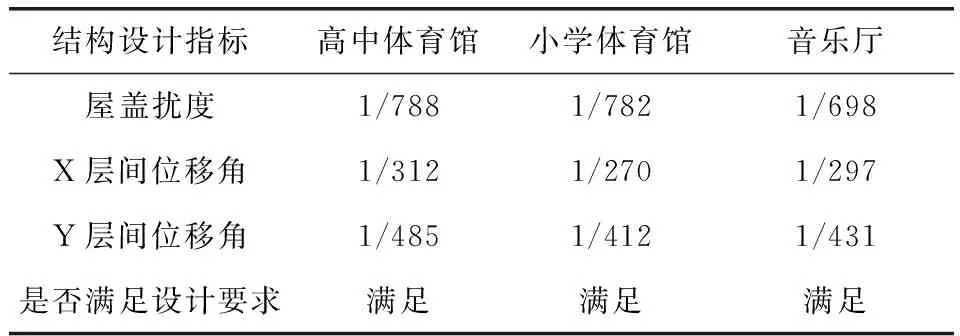
表5 位移刚度验算
4 结论
(1)参数化设计是解决大跨空间结构找形建模问题的有力工具,能大大减小建筑修改带来的重复工作量,大大提高结构设计效率。
(2)在进行参数化建模中,将一些常常需要调整的结构参数进行参数化,方便进行结构调整。
(3)建立的通用网架、网壳和管桁架生成Grasshopper程序能根据建筑表皮快速生成网架、网壳和管桁架。
(4)对于存在多个相似楼栋的情况,参数化建模能通过修改变量,快速得到相似楼栋模型,大大提高结构建模效率。
