分离变量法和函数逼近法在偏微分方程的解法分析

杨冬成

（江苏联合职业技术学院，江苏 盐城 224001）

目前，在许多领域中数学模型都可以用偏微分方程来描述。同时许多重要物理和力学的基本方程本身就是偏微分方程，例如热传导方程[1，2]。随着物理科学研究现象在广度和深度上的扩展，偏微分方程的应用范围更加广泛[3−5]。从数学自身的角度来看，偏微分方程的求解促使数学在函数论、变分法、级数展开、常微分方程、代数、微分几何等各个方面进行发展[6]。分数阶微积分是近十几年的研究热点，例如一些由分数阶微分方程表示的问题比起用经典微分方程表示更深刻、更贴合实际[7]。分数阶微积分隐隐有取代经典微积分之势。而本研究主要使用不同的方法对一个分数阶偏微分方程予以求解，并对所用方法予以比较。

1 热传导方程求解方法原理

1.1 分离变量法原理

分离变量法是将一个偏微分方程分解为两个或多个常微分方程，其中该方程只含一个变量。将方程中含有各个变量的项分离开来，并将原方程拆分成两个或多个更简单的只含有一个自变量的常微分方程。再运用线性叠加原理，将非齐次方程拆分成多个齐次的或易于求解的方程。边值问题变量x的取值范围总可以规范化为[0,1]。分离变量法只能对齐次边值条件直接求解，非齐次边值条件需要通过变换转化为齐次边值条件（可参考文献[1]）。此处以方程(1)(fi(t)=0,i=1,2,g=0)为例说明该方法。

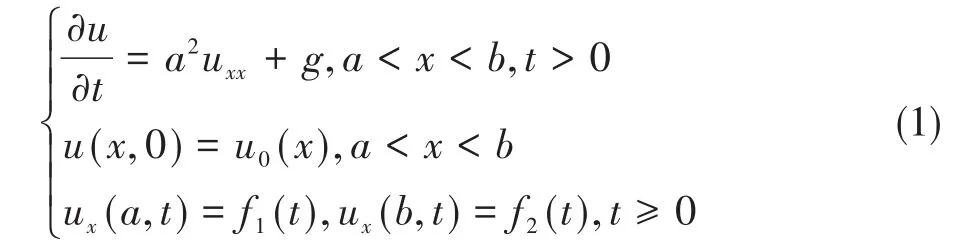
令u(x,t)=X(x)T(t)，即假设方程(1)的未知函数具有变量分离的特点。代入方程(1)中得到

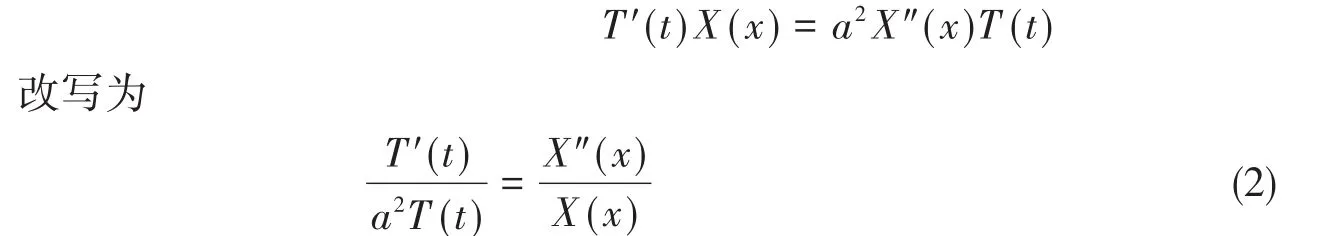
可以注意到左边是t的函数，右边是x的函数（a是常数）。因此，仅当两边都为常数才能相等。故可以设该常数为λ，于是有

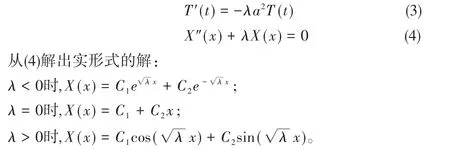
但是，把零边值条件代入，发现必须要求λ＞0并且满足：λ=n2π2,n=0,±1,…。

记λn=n2π2，对于此λn代入(3)，解出T(t)=Ane−λna2t,An是积分常数。这样

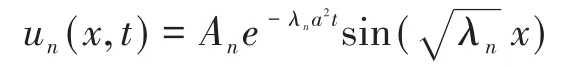
而线性方程具有可加性，因此，可以得到叠加之后的解：

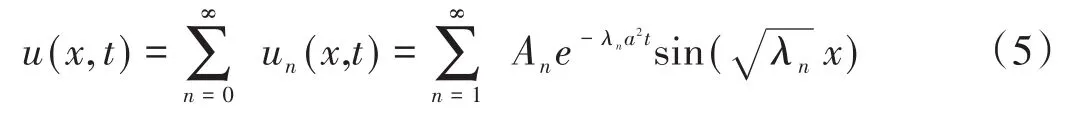
再把初值条件作傅里叶级数展开，求出系数An，就最终得到了方程的解。

1.2 积分变换法原理

积分变换是把某一类的函数f(ξ)经过积分F(s)=∫K(ξ,s)f(ξ)dξ变成另一类的函数F(s)的运算。而本研究主要使用积分变化法中的傅立叶变换（Fourier变换）和拉普拉斯变换（Laplace变换）。

1）Fourier变换的性质：

线性性质，设F1(ω)=F[f1(t)]，F2(ω)=F[f2(t)]，其中α和β是常数，则F[αf1(t)+βf2(t)]=αF1(ω)+βF2(ω)。

位移性质F[f(t±t0)]=e±iωt0F[f(t)]。

微分性质，若f(t)在(−∞,+∞)上连续或者只有有限个可去的间断点，并且当|t|→ +∞时，f(t)→ 0，则F[f′(t)]=iωF[f(t)]。

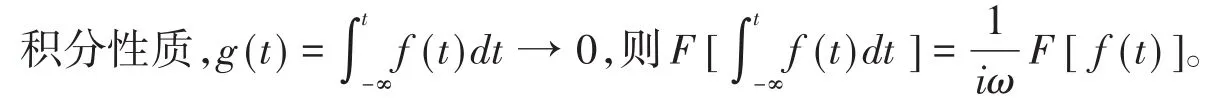
2）Laplace变换的性质：

1.3 函数逼近方法原理

Adomian分解法原理如下，把分数阶微分方程改写为：

Dαu=Lu+f(t)+N(u),n−1≤α＜n

其中L代表线性算子，N代表非线性算子，f(t)则是与u无关的项。两边作用逆算子Jα，成为，其中把初值条件代入，第一项是确定的。令u(t)=，代入改写后的方程得下式：

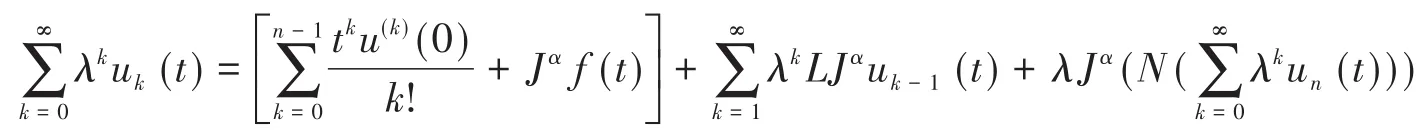
把最后一项展开为λ的幂级数，记为。把上式中λ各幂次的系数收集起来，可得出，。递推方式就可以解出各个uk(t)，从而得到方程近似解。

2 生物传热微分方程的求解结果

2.1 生物传热方程概述

经典的Pennes传热方程是：

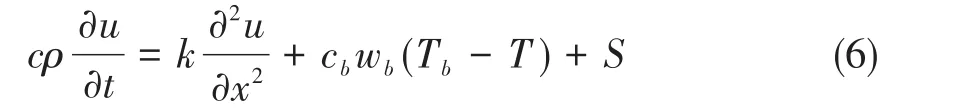
其中ρb,cb,wb分别是组织密度，组织比热和血液灌注率，而Tb,S分别是动脉血液温度和环境作用的热量，S一般可由代谢产热及组织内热构成[2]。生物体胳膊、腿部近似为圆柱形，躯干也可看作圆柱，因此，适用圆柱上的偏微分方程。可以使用如下方程：

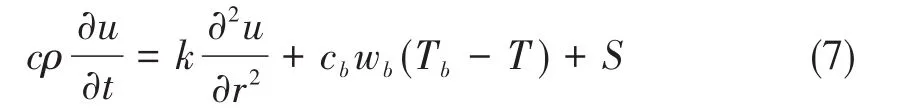
Feller[3]研究一般的扩散问题，把生物组织内热量传导引起的变化由QT=kDαxu表示时，就得到分数阶热传导方程：

显然，当α=2就成为经典Pennes方程。

Povstenko[4]则利用了不同的Fourier定律，这里0≤α＜ 1,导数是Caputo导数。得到另一种分数阶热传导方程是：

显然，当α=0也是经典Pennes方程。但是要注意，(8)与(9)是完全不一样的方程，它们的分数阶导数作用对象不同。本文考虑(9)即时间分数阶导数方程问题，并假设S=0：

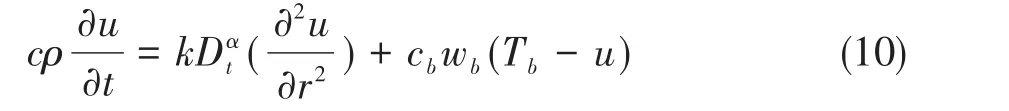
借助文献[5]的数据，假设该方程的初边值条件为：

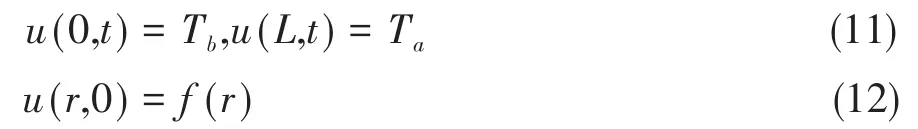
其中L是生物体中心与表皮的距离，坐标原点在中心血管位置，Ta是环境温度。作变换v=u−Tb，初边值问题化为：

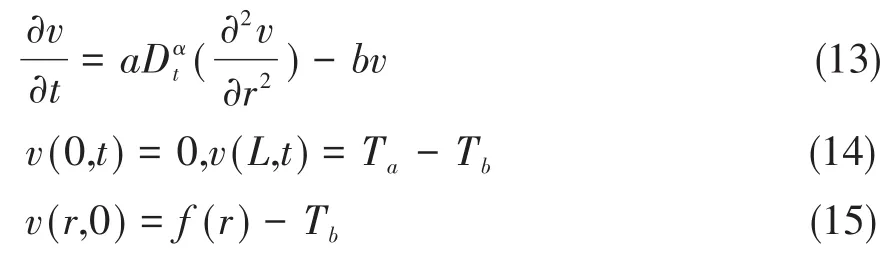
2.2 傅里叶-拉普拉斯变换求解方程

2.3 分离变量法求解[6]

2.4 函数逼近方法求解

3 结论

本研究以经典的Pennes传热方程求解为例。采用了有限Fourier变换、Fourier−Laplace变换和分离变量法等方法求解方程。其次，运用函数逼近方法中的Adomian分解法求出了方程的近似解。