Excel在一元线性回归分析中的应用

杨雄 曾智

（娄底职业技术学院，湖南 娄底 417000）

回归分析是在研究现象之间相关分析的基础上，对自变量x和因变量y的变动趋势拟合数学模型进行数量推算的一种统计分析方法[1]。在客观世界中，寻找变量之间的关系，大致可以分为两种类型：一是反映变量之间的确定性的关系，称为函数关系；二是变量之间存在着关系，但不是确切的函数关系，可是变量之间又存在某种密切关系，然而又不能由一个（或一组）变量的值精确地求出另一个变量的值，称这种非确定性关系为相关关系。在相关关系中，假设x,y是两个变量，其中x是自变量，y是因变量，而自变量x的取值是非随机的普通变量，它是人为的可控制的变量，称为可控量，因变量y由于随机误差等因素的影响，取值是随机的，称为随机变量，但服从一定的概率分布。进而当自变量x是非随机的可控变量时，自变量x与因变量y关系的分析称为回归分析。

回归分析法属于因素分析法的一种，在掌握大量观察数据或历史数据的基础上，利用数理统计方法建立因变量y与自变量x之间的回归关系函数表达式。在有些专业中，开设了经济数学课，包含一元回归分析内容，其中会计专业课会讲到成本预测，成本预测需要建立回归方程，但在成本预测的计算中面对复杂的数据，同时涉及要素也繁多，此项工作任务繁重，因此需要借助相应工具来简化计算提高工作效率。而运用Excel软件能够把烦琐、主观的核算与分析内容简单化、客观化、图表化，这无疑是一种较好的方法。而且使工作更加便利、快捷，并能有效减少错误发生的概率。因此以成本预测为案例，对回归分析内容及应用Excel进行回归分析的实际操作进行研究。

1 一元线性回归模型建立过程及定义

1.1 回归分析的建立过程

回归分析是利用历史数据或观察数据对模型中的函数值f(x)进行估算，探讨随机误差项的分布特征，进而应用模型进行预算，一般建立一个回归分析方程包括以下几个过程：通过样本数据，判定因变量x与自变量y的关系，确定回归模型的f(x)的函数形式；利用样本数据拟合回归模型的f(x)中的未知参数；确定估计量与随机误差的分布特征；进行拟合优度检验，验证是用历史数据或观察数据x值对预测y值的拟合程度；利用回归模型进行未来预测或控制。预测是通过回归方程，对已知的值进行相应值计算，而在回归方程中参数的计算、分析及预测值的计算运用传统的数学方法实践起来困难，可运用Excel进行替代，这正是运用Excel进行回归分析的意义所在。

1.2 一元线性回归模型的定义

定义1设x是可控变量，Y是依赖于x的随机变量，假定

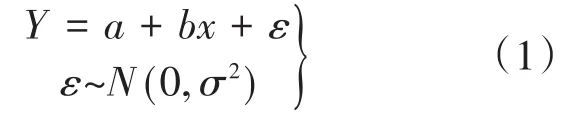
其中未知参数a,b及σ2都不依赖于x，则（1）式称为一元线性回归模型[2]。

定义2当给定x一组不完全相同的值x1,x2,…,xn时，对Y分别在x1,x2,…,xn处进行独立观测，其观察结果记为Y1,Y2,…,Yn，则Y1,Y2,…,Yn是相互独立的随机变量，则称(x1,Y1),(x2,Y2),…,(xn,Yn)是模型（1）的一个样本，相应的样本值记为(x1,y1),(x2,y2),…,(xn,yn)。

此时，由模型（1）式有

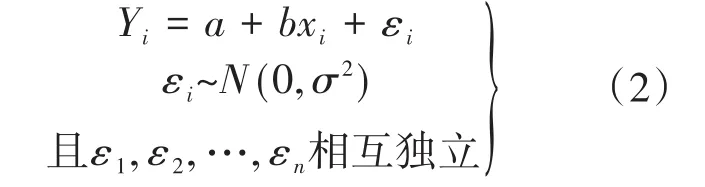
则（2）式称为一元线性回归模型（1）式的样本形式，也称为一元线性回归模型。由(xi,yi)(i=1,2,…,n)可求得（1）式中的未知参数a,b的估计值，再代入（1）式中，进而可得回归方程。

1.3 a,b值的具体求解过程

在一元线性回归分析中，y的值是随着x的值变化而变化，事实上一个实际的x值会对应一个实际y值（称y实际），若x与y存在直线关系，想求出此条直线方程，每一个实际x值有一个直线预测值（称预测）与之对应，进而进行线性回归分析的目的就是要求y实际与预测之差的平方和最小，即下式的和最小。

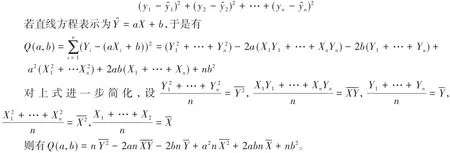
Q分别对a,b求偏导数，并令偏导数等于0，解方程组可得：，把a,b值代入直线方程，即得回归方程[3]。

2 模型的提出及判定是否存在线性相关性

2.1 回归分析成本预测模型的提出

在回归分析模型建立之前，先探讨一个成本预测模型，若已知某企业2010年—2019年的产量与实际成本数据如图1（产量单位万件，成本单位万元），根据成本与产量的数据，是否可以发现什么内在的规律，假设存在规律，是否可以根据规律及假设2021年的产量估算成本。不防假设预测模型如下（也有可能是其他函数模型，这是只分析简单的一次函数模型）：Yt=a+bxt+ε。

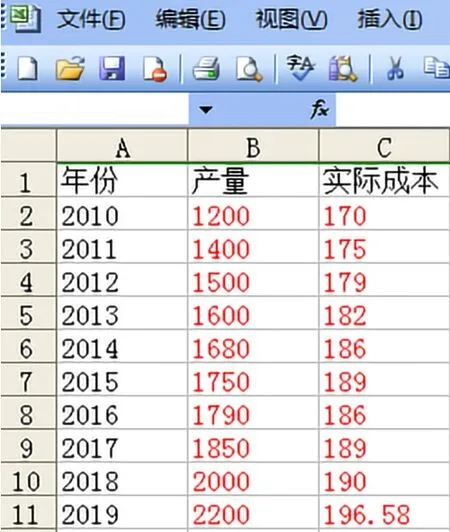
图1 某企业2010年-2019年的产量与成本图

其中：Yt是总成本，a固定成本，b是单位业务量所需的变动成本，ε为残差，xt是产量。若能利用2010年−2019年的数据确定预测模型中的a、b数值，则就可以预测一定产量x所需发生的总成本Y。接下来的问题就是如何求出a、b数值，若求出a、b的值，且假设2021年生产产品3 000万件时，就可以预测其成本。

2.2 相关系数的定义及其判断变量之间线性关系程度

以上提出的问题，并不一定保证产量与实际成本是线性关系，即两个变量之间是否存在一元直线回归方程的形式，首先应判断怎样的两个变量之间才有可能存在一元直线回归关系，只有存在线性关系的两个变量，求出的一元线性回归方程，在实际应用中才有意义。进而要对变量之间的线性相关的紧密程度进行判断，其中相关系数R或R2就是判断两个变量之间线性相关的密切程度的[4]。并且R和R2分别由定义3和定义4给出。

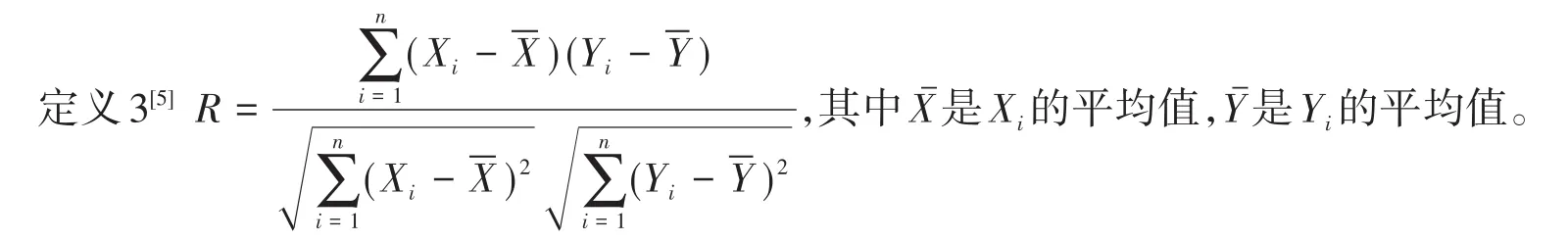
R的取值范围是[−1,1]，R的绝对值越接近于1，x与y两个变量之间的线性相关性越强，R的绝对值越接近于0，x与y两个变间之间的线性相关性越弱。相关系数R在Excel中有三种计算方法：Correl函数；Pearson函数；使用数据分析工具，即点击数据选项卡下数据分析功能，在弹出的对话框中的相应输入区域选择数据范围，选择输出区域为期望放置结果的位置，回车后输出结果。具体判断变量之间的性线关系程度见表1。

表1 相关程度

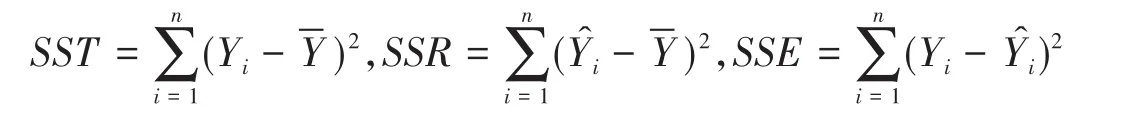
若SSE=0，则R2=1，即y的变化完全由x的变化引起，没有其他的因素影响y，因此可由x完全解释y的变化，也就是变成了一次函数关系。若R2靠近0，则x与y之间可能不存在线性关系。

2.3 判断产量与成本是否存在线性关系

在Excel工作表中输入数据图1，并作出散点图图2，从散点图2上可以看出产量与实际成本呈现出直线趋势。这只是定性的判断了产量与成本具有线性关系，还需要进行定量的计算。Ex⁃cel软件中需有“数据分析”工具，若没有，需要先安装。安装方法：在“Excel选项”中选中左侧栏的“加载项”，再单击右侧栏最下面的“转到”按钮，在弹出的“加载宏”窗口中选中“分析工具库”选项，单击“确定”按钮，按系统提示自动安装，安装完成后，重启Excel系统，再打开，则在“数据”菜单下出现“数据分析”工具[6]。然后进行后面二步操作，点击数据工具中相关系数，选择数据以及输出区域，点击确定，即可出现图3的结果。从图3可知相关系数R=0.976054，说明产量与实际成本具有高度线性相关性。既然产量与成本具有高度的线性关系，则可以用Excel求解一元线性回归方程。

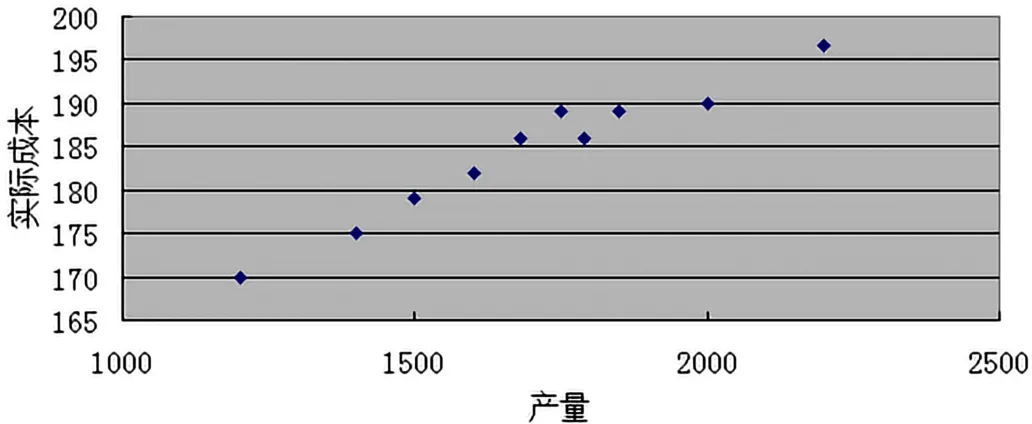
图2 原始数据散点图

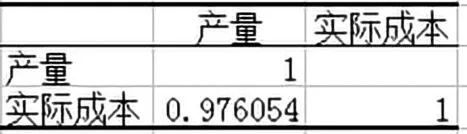
图3 相关系数计算结果

3 运用Excel进行一元回归分析实例操作

3.1 应用Excel中的函数计算回归方程

用函数Slope（y值数列，x值数列），返回线性回归直线的斜率a，用函数Intercept（y值数列，x值数列），返回截距b，或用函数Linest（y值数列，x值数列，逻辑值（常数），逻辑值（统计）），可以直接求出回归方程的参数。这里例举Linest函数的应用，如图4选定E1：F5，在Excel地址栏中输入=Linest(C2:C11,B2:B11,true,true)，然后同时按下组合键ctrl+shift+enter，进而得到图4的结果，可以读出a=139.493,b=0.0264，即回归方程为

y=139.493+0.0264x

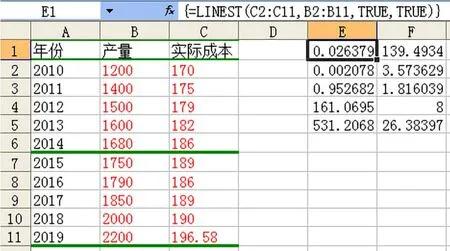
图4 Linest函数操作图

3.2 在Excel中应用数据分析工具求解回归方程及其输出数据的解释

根据图1的数据，在Excel中，应用数据分析工具中的回归分析，可以求出相关系数和回归直线方程。在数据分析工具中打开回归对话框，如图5，在Y值输入区域输入$C$2:$C$11（可以直接选取区域），在X值输入区域输入$B$2:$B$11（可以直接选取区域），并指定输出区域，勾选残差、线性拟合图，然后确定，进而得到表2、3、5、6及图6、7分析结果。从表2中可以看出相关系数R2=0.952682，调整后值为0.946767，两者数据都接近于1，则可知产量和成本具有高度线性关系。也可以读取F的检验值为161.07，而F0.05(1,10−2)=5.32＜161.07，则可知产量x与成本y的线性回归方程显著。同时可读取a=139.493,b=0.0264，进而可得回归方程为y=139.493+0.0264x。

图5 建立回归模型

以下对在Excel中数据分析结果的参数及图进行详细解读。

从表2可以读出相关系数、测定系数、校正测定系数、标准误差和样本数目。相关系数是Multiple对应的值，即R=0.976054399；测定系数（或称拟合优度）是R Square对应值，即R2=0.9760543992=0.952682189；校正测定系数是Adjusted对应值，即Ra=0.946767463，标准误差（standard error）的值是S=1.816038761；样本数目是观测值，即n=10。当然其中有些值可直接由公式计算。

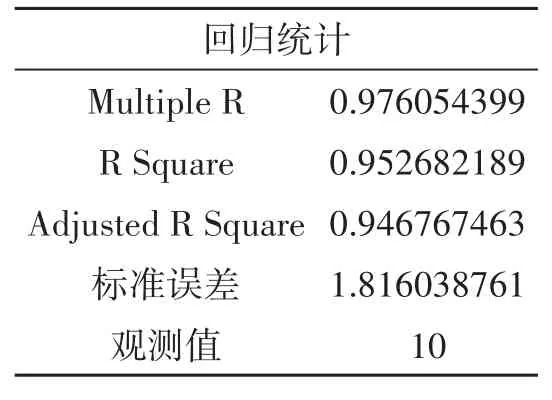
表2 回归统计表

1）校正测定系数可以用公式（3）计算。

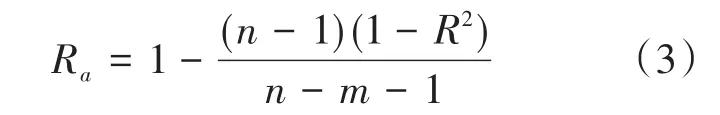
其中n是样本数，m是变量数，R2是测定系数，对于本回归模型，n=10,m=1,R2=0.952682189，将这些值代入（3）式即可得校正测定系数Ra值。

2）标准误差可以用公式（4）式计算。

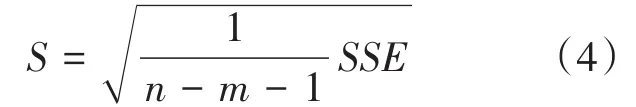
其中SSE是残差平方和，从表3（方差分析表）中读出SSE=26.38397并与n=10,m=1，代入（4）式可得S值。

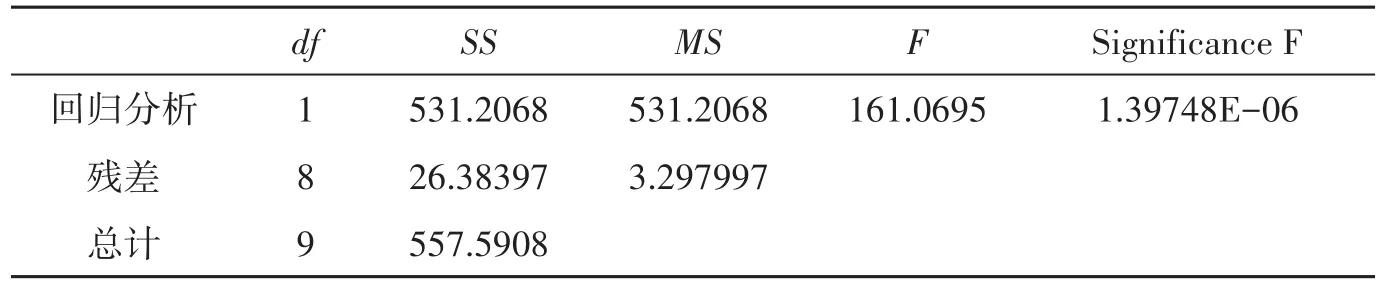
表3 方差分析表（ANOVA）

表3可以读出自由度、误差平方和、均方差、F值、P值等。自由度（degree of freedom）是df对应的值，其中第一个数是变量数目，即dfr=m=1，第二个数是残差自由度dfe=n−m−1=8，第三个数是总自由度dft=n−1=9；误差平方和（或称变差）是SS对应的值，其中第一个数是回归平方（或称回归变差）SSR=531.2068，第二个数值残差平方和（或称剩余变差）SSE=26.38397，第三个数值是总偏差平方和（或称总变差）SST=557.5908；均方差是MS对应的值，第一个数是回归均方差MS=531.2068，第二个数是剩余均方差MSE=3.297997；F=161.0695；P=1.39748*10−6。其中有些值可以直接由公式计算。

1）回归平方和，它表征是因变量的预测对其平均值的总偏差。

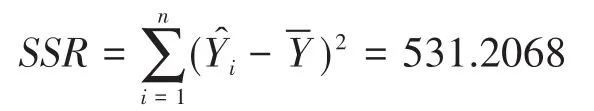
2）残差平方和，它表征的是因变量对其预测值的总偏差，数值越大，拟合的效果越差，y的标准误差即由SSE值求出。

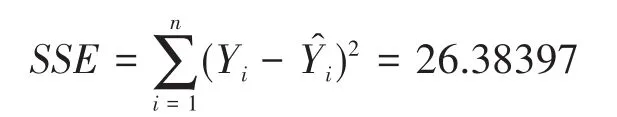
3）总偏差平方和，它表示的是因变量对其平均值的总偏差。

4）测定系数，它表示的是回归平方和占总偏差平方和的比重，数值越大，拟合效果越好。

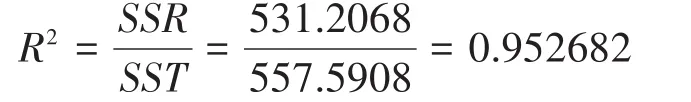
5）均方差，它是误差平方和除以相应的自由度得到的商，有回归均方差MSR和剩余均方差MSE，MSE的值越小，拟合效果越好。

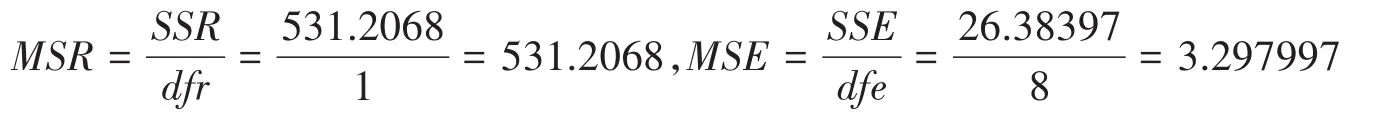
6）F值，它是用于线性关系的判定，一元线性回归中F的计算公式（5），将R2=0.952682，dfe=10−1−1=8，代入（5）式中，即可得F=161.0695。

7）P值，Significance F对应的值是在显著性水平下的Fα临界值，也就是P值，也为弃真概率，所建模型为假的概率，则1−P是所建模型为真的概率，当然P值越小越好，本模型中P=0.00000139748＜0.0001，故置信度达到99.99%以上。

表4中可以读出回归模型的截距、斜率及其有关的检验参数。回归系数是Coefficients对应的值，即截距a=139.493398和斜率b=0.026378669，因此建立的模型是=139.4934+0.0264xi或=139.4934+0.0264xi+εi；标准误差，a=3.573629，=0.002078，其值越小，参数的精确度越高；统计量t值是t Stat对应的值，用于对模型参数的检验，需要查表才能决定；参数p值（双侧）是p value对应的值，对P值的分析如表5，对于本模型P=0.0000014＜0.0001，即可以认为在α=0.0001的水平上显著，或者置信度达到99.99%。P值检验与t值检验是等价的，但p值不用查表，显然要方便得多。

表4 回归参数表

表5 P值分析表

表4中最后几列给出的回归系数以95%为置信区间的上限和下限。可以读出，在α=0.05的显著水平上，a的取值范围是131.2526＜a＜147.7342，b的取值范围是0.02159＜b＜0.03117。

其中有些量可以直接用公式计算。

1）t值在一元线性回归分析中，F值、t值、相关系数R是等价，在相关系数检验中已有这部分信息，但是在多元线性回归分析中，t检验是不可能缺省的。其中回归系数与其标准误差的比值就是t值。

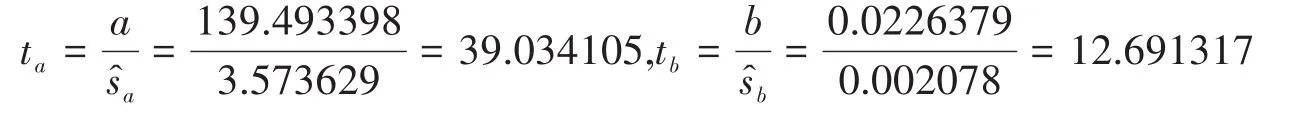
一元线性回归分析中的t值可以用相关系数值或测定系数值进行计算，如公式（6），本模型中，将R=0.976054，n=10，m=1代入（6）式可得t=12.691317

表6是选择输出内容，若选择残差项则有表6内容，输出结果包括，第一列观测值序号（用i表示），第二列因变量的预测值（用表示），第三列残差（用ei表示）以及第四列标准残差值。

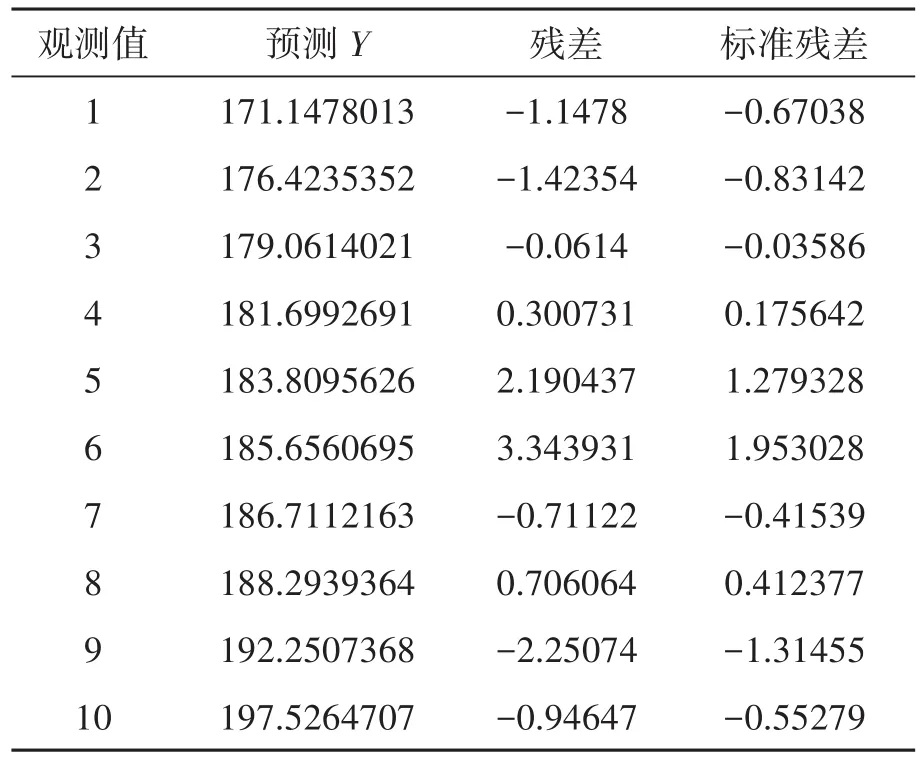
表6 残差输出结果

1）预测值可由回归模型=139.4934+0.0264xi求解，式中xi是图1中的数据，从图1可知x1=1200，代入模型中可得=139.4934+0.0264xi=139.4934+0.0264*1200=171.1478。

其他预测值都可以用同样方法求解。

2）残差ei的计算公式为ei=yi−。

从图1可知y1=1700，代入上式可得e1=y1−1=1700 − 171.1478= −1.1478。

其他残值可以用同样方法求解。

3）标准残差是由残差的数据标准化后的数值，应用均值命令average及标准差命令stdev容易计算出结果，残差的算术平均值为0，标准差为1.71218，利用标准化命令standardize（残差，均值，标准差）立即算出表6中的结果。当然，也可以利用数据标准化公式进行逐一计算。将残差平方再求和，便可得残差平方和（也称剩余平方和），则有

应用Excel中的命令sumsq（求平方和函数）容易求出以上结果。

图6与图7是以产量xi为自变量，以残差ei为因变量，作散点图，可得残差图（图6）。残差点列的分布越没有趋势（没有规则，即越是随机），得到的回归结果就越是可靠。以产量xi为自变量，用实际成本yi及其预测值为因变量，作散点图，可得线性拟合图（图7），实际成本与预测成本越重叠在一起，说明回归方程越可靠。

图6 残差图

图7 线性拟合图

3.3 在Excel中应用所求回归方程进行预测

前面通过多种参数分析说明预测模型中的产量与成本构成线性关系，应用Excel中的函数计算或数据分析工具都得到回归方程为y=139.493+0.0264x，并应用数据分析工具可以得到残差数据表，说明预测值与真实值有一点差距，但残差值满足回归检验范围，满足预测的要求，所以可以应用前面计算得到的回归方程进行预测计算。从回归方程y=139.493+0.0264x可知该产品的固定成本为139.493万元，单位变动成本为0.026 4万元，因此假设2021年生产3 000万件，则该产品的总成本为139.493+0.0264*3000=218.693万元。

4 多元线性回归分析

多元线性回归分析是研究因变量和多个自变量的线性关系，这种线性关系可用数学模型来表示，设因变量为yc，因变量yc与自变量x1,x2,x3,…xn之间存在线性关系，可用多元线性回归方程来表示这种关系。设多元线性回归方程为：yc=a+b1x1+b2x2+b3x3+…+bnxn+ε。

式中a、b1、b2、b3、…、bn为线性回归方程和参数，ε为残差。具体的案例及参数与以上的一元回归分析一样可在Excel中进行。

案例1某地区2014年到2020年一种太阳能热水器销售额，广告费和利润资料见表7。

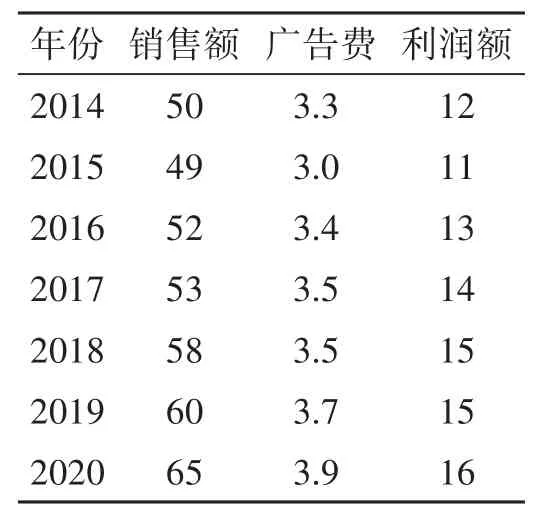
表7 某地太阳能热水器销售资料（单位：百万元）

分析：

1）A1：D8区域内输入表7数据，即在单元格B2：B8中输入x1值（销售额），在单元格C2：C8中输入x2值（广告费），在D2：D8中输入y值（利润额），其中要求区域由列数据组成。

2）填写如图5“回归”对话框，其中$D$2:$D$8输入到“Y值输入区域”，$B$2:$C$8输入到“X值输入区域”。同一元回归分析一样，可得到一系列分析数据及回归分析正态分布图，这不给出分析图及表，只给出结果，a=−5.6259,b1=0.1275,b2=3.5407。

3）建立回归模型y=a+b1x1+b2x2+ε，将通过Excel回归分析得到数据代入即可得到回归方程：y=−5.6259+0.1275x1+3.5407x2+ε，进而可用该模型对未来的利润进行预算。这里只例举了两个自变量的回归模型在Excel中进行计算，实质三个以上的自变量都可以用同样的操作方法解决。

5 总结

在Excel中，进行多元回归分析的操作过程类似于一元线性回归分析，并且分析所得结果相似，变量数m≠1，t值和F值等统计量不等价于R值，进而不能应用相关系数求解。若用软件Spss进行回归分析，分析结果与Excel分析结果大同小异，只是Spss分析结果中出现更多的统计量及显示方法上有差异。因此若能读懂Excel的回归分析中各参数的意思，则就可以读懂Spss回归输出结果的大部分内容。采用回归分析法进行成本预测的定量分析，运用Excel软件实现预测总成本的计算，在操作过程中，有助于理解数学知识，提高动手能力。