基于深度自编码器的PRI调制方式识别的一种新方法

李雅朦，武艳伟，裴晓帅，宋 扬

（中国电子科技集团公司信息科学研究院，北京100086）

0 引言

随着电子战信号环境的复杂化及雷达信号形式的多样化，依靠传统的五大参数法（脉宽、载频、到达角、幅度和到达时间）进行信号分选时不可避免地会产生参数模糊，影响信号分选的效果[1]。如果能对分选出的每个雷达脉冲序列的PRI调制特性进行分析，一方面有助于解决参数模糊问题，提高信号分选的可靠性[2]；另一方面，PRI调制形式反映了雷达信号的某些特性，对PRI调制类型的正确识别将有助于推定雷达的用途与性能，实现辐射源识别。因此，对复杂体制的PRI调制方式进行识别是ESM中的重要任务之一。

一般而言，复杂体制PRI调制识别算法应可以解决如下3个问题:

1)脉冲样本数量少时，可对PRI调制方式进行有效识别[3]。例如，对于搜索雷达，其旋转一周，电子侦察接收机只能接收到近100个脉冲。

2)存在TOA测量误差，噪声脉冲条件下，可对PRI调制进行有效识别[4]。由于电子侦察中所截获信号的信噪比通常较低，加之接收机的性能限制及去交错算法本身的局限性，TOA的估计误差、噪声脉冲的存在是无法避免的。

3)所选取的分类特征应具有一定的不变性[5]。所谓分类特征的不变性是指调制分类特征应基本不受PRI调制参数变化的影响。因为同一种PRI调制方式其具体的调制参数是变化的，而用来区分不同的PRI调制的特征若受参数变化影响较大，将导致分类识别算法的顽健性下降。

针对PRI调制类型识别中出现的问题，本文提出了一种基于DAE（深度自编码器）的类型识别新方法。该方法主要由2部分组成，首先采用滤波器思想将不同调制方式的PRI序列特征显性化，然后对预处理之后的序列通过等间隔采样进行数据降维，在不丢失数据特征的前提下尽可能缩短网络训练的时间，达到快速识别分类的目的，最后将样本送入DAE模型进行样本数据训练，最后采用softmax分类器完成分类识别任务。

1 数据预处理

雷达信号脉间PRI调制是指雷达脉冲信号重复间隔的有规律变化。脉间PRI调制方式主要有固定、参差、抖动、滑变、正弦调制及驻留与切换等，对于抖动、滑变、正弦调制及驻留与切换等PRI调制方式，在去交错处理时只能粗略地识别成“复杂”类型，无法做出具体的判断[6]。在侦察接收机接收到脉冲序列后，与传统的识别流程不同，本文省略对脉冲序列进行特征提取和去交错等步骤，直接将截获的中频数据经过简单的预处理后送入神经网络进行训练及分类识别。因为考虑到对于搜索雷达，其旋转一周，电子侦察机只能收到近100个脉冲，所以本文提出的算法可以在脉冲样本数量较少时，对PRI调制方式进行有效识别。

通过对雷达脉冲信号PRI序列特点的分析，可以得知，对于不同调制方式的PRI，在中频数据中主要体现在每个脉冲的到达时间不同，如果不进行数据预处理，在中频数据中就存在很多干扰信息，如脉内调制方式、脉内高斯噪声、脉冲强度，一定程度上影响了PRI调制方式识别的识别率和识别速度[7]。针对此问题，本文提出了一种基于滤波器思想的数据预处理方法，其数学模型为：

设截获到的脉冲序列的采样幅值集合A作为滤波器输入，滤波器的响应为H，输入与响应之间的数学关系为：

根据（1）式得到的响应集合H过滤掉了对于PRI调制识别无效的脉内信息，然后根据响应集合H的总长度L，对集合进行等间隔采样，在保留数据特征的同时降低数据维度。以滑变PRI调制方式说明以上流程，如图1所示。

图1 预处理流程

PRI序列的图片经过放大后可以看到在每个脉冲内的调制方式为LFM（线性调频），如图2所示，而图1的滤波后PRI序列和采样后PRI序列中是不包含脉内调制信息的。

图2 原始信号脉内信息

在图1中，原始PRI序列的点数为120 000，滤波后PRI序列的点数为12 000，再经过采样后的PRI序列点数变为1 000，从点数的变化可以看到，预处理过程对长序列数据也起到了很好的降维效果，在保留PRI调制本质特征信息的同时有助于降低后期的网络训练速度及网络维度。

2 DAE模型分析

2.1 DAE模型介绍

自编码器是一种理想状态下输出和输入相同的特殊神经网络算法，输出向量是对输入向量的复现[8]。整个输入层和隐藏层称为编码器，输入向量映射到具有不同隐藏层维度的向量[9]。整个隐藏层和输出层称为解码器，隐藏层的向量映射到输出向量。隐藏层向量可以复现输入向量。自编码器的主要功能就是生成输入数据的主要特征表示向量。

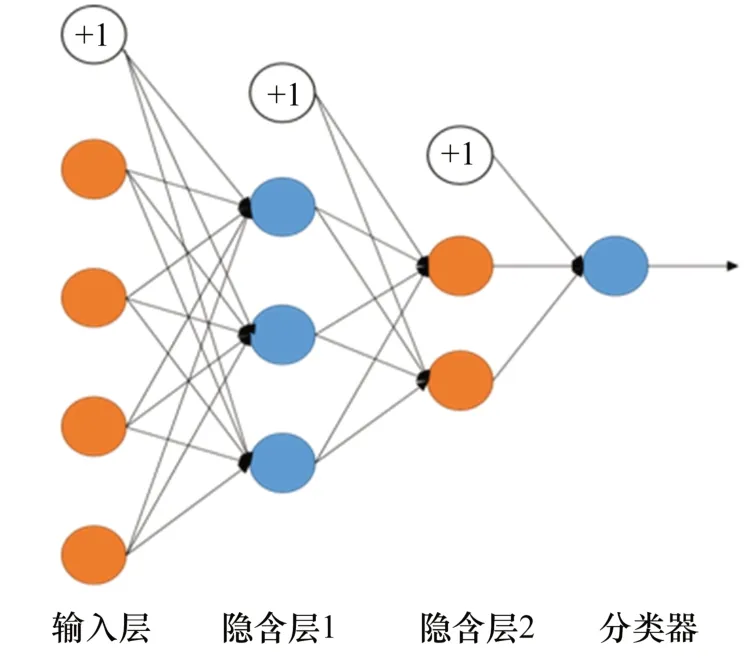
图3 含2个隐藏层的深度自编码器

深度自编码器是由2个或2个以上的单个自编码组合而成的，实则就是增加了隐藏层的数量，经过贪婪算法预训练和多层非线性网络，最后从复杂高维的输入数据中学习到不同维度和层次的抽象特征向量[10]。深度自编码器中的每一个隐藏层都是输入特征的另一种表示，并降低了输入数据的维度，具有提取输入特征的强大学习能力，如图3所示。整个深度自编码器的训练过程包括2个步骤[11]：第一步是预训练，通过无监督学习方式去训练单个自编码器，每当上一层训练完时，输出被当作下一层的输入，再继续训练，直到训练完整个隐含层，最后输出。假设有3个隐藏层的深度自编码器，X表示输入要素向量，hi表示每个隐藏层的表示向量，X′,h1′和h2′表示单个自编码器重建的输出向量，w和wT都是权重矩阵。预训练的具体步骤如下，如图4所示。

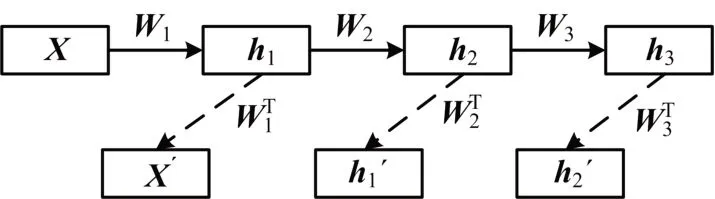
图4 预训练含三个隐藏层的深度自编码器图

1）用无监督训练的方式训练深度自编码器的第一隐藏层；

2）上一个隐藏层训练完成的输出被视为下一个隐藏层的输入，再以无监督方式进行训练；

3）重复执行步骤2），直到把所有的隐藏层都训练结束。

第二步是微调。是在预训练结束后，再训练整个深度自编码器，并利用误差反向传播调整整个系统的参数，使得权值和偏置值都达到最优。

2.2 网络设计

分别构建3个3层的自编码器，其中第1个自编码器的结构为：由1 000个单元组成的输入层、由128个单元组成的全连接隐含层、由1 000个单元组成的重构层；第2个自编码器的结构为：由128个单元组成的输入层、由64个单元组成的全连接隐含层、由128个单元组成的重构层；第3个自编码器的结构为：由64个单元组成的输入层、由32个单元组成的全连接隐含层、由64个单元组成的重构层。深度自编码器网络的设计过程如下：

1）先分别计算3个自编码器中每层单元的权重和偏置，作为3个自编码器的初始化权重值和偏置值：

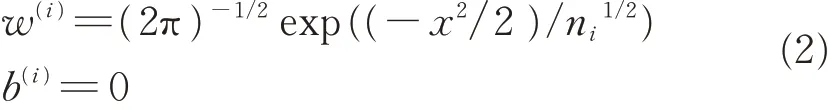
式中，w(i)表示自编码器中第l层的权重，x表示每次初始化权重值和偏置值时在范围内随机选取的一个不同的数，ni表示自编码器中第l层的单元总数，b(i)表示自编码器中第l层的偏置。

2）从样本矩阵中取一批行向量输入到搭建的第1个自编码器中进行预训练，将第1个自编码器隐含层单元的输出值组成第1个特征矩阵；利用损失函数公式，计算第1个自编码器的损失值，利用自编码器权重和偏置的更新公式，用第1个自编码器损失值更新其权重和偏置后抛弃第1个自编码器的重构层。

所述损失函数公式如下：

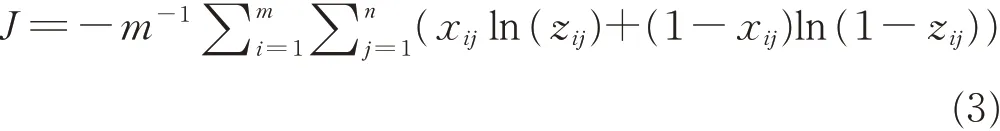
式中，J表示自编码器的损失值，m表示预训练的批大小，表示自编码器的输入层的单元总数，xij表示输入数据，zij表示自编码器的输出值。所述自编码器权重和偏置的更新公式为：

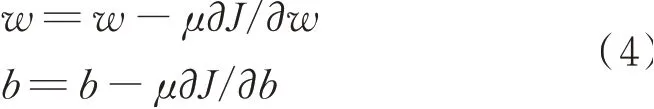
式中，w表示自编码器的权重，b表示自编码器的偏置，μ表示值为0.1的学习率。

3）将第1个特征矩阵输入到第2个自编码器中进行训练，将第2个自编码器隐含层单元的输出值组成第2个特征矩阵；利用损失函数公式，计算第2个自编码器的损失值，利用自编码器权重和偏置的更新公式，用第2个自编码器损失值更新第1个自编码器的权重和偏置后抛弃第2个自编码器的重构层。

4）将第2个特征矩阵输入到第3个自编码器中进行训练；利用损失函数公式，计算第3个自编码器的损失值，再利用自编码器权重和偏置的更新公式，用损失值更新第3个自编码器的权重和偏置后抛弃第3个自编码器重构层。

5）将第1个自编码器的输入层、第1个自编码器的隐含层、第2个自编码器的隐含层、第3个自编码器隐含层、由4个单元组成且激活函数为Softmax函数的输出层，依次连接组成一个5层结构的深度自编码器网络。

6）将训练集分批输入深度自编码器网络，利用深度自编码器网络的损失函数公式，计算深度自编码器网络的损失值，再利用深度自编码器网络权重和偏置的更新公式，用损失值更新深度自编码器网络的权重和偏置，完成深度自编码器网络的微调训练。

所述深度自编码器网络的损失函数公式为：

式中，C表示深度自编码器网络的损失函数值，p表示训练的批大小,q表示深度自编码器网络输出大小，yij表示标签数据，aij表示深度自编码器网络输出。

所述深度自编码器网络权重和偏置的更新公式为：

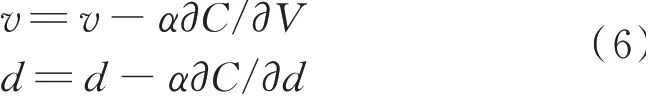
式中，C表示深度自编码器网络的损失函数值，v表示深度自编码器网络的权重，d表示深度自编码器网络的偏置，α表示为值0.01的学习率。

3 实验仿真

基于深度学习的PRI调制方式识别的处理流程主要包括2部分[12]：训练过程和测试过程。训练阶段首先根据数据特性进行降维和采样的预处理；然后训练深度学习模型中的参数，使模型在尽可能保存信息的同时可以较好地表达当前的训练数据。在测试阶段，对测试数据进行同样的预处理，由模型对测试数据提取可分性的特征，最后由分类器对测试数据特征进行判决，最终输出测试数据的识别结果。

3.1 实验数据及预处理

本实验采用的4种PRI调制类型分别为：抖动、正弦调制、驻留与切换、滑变，如图5所示。

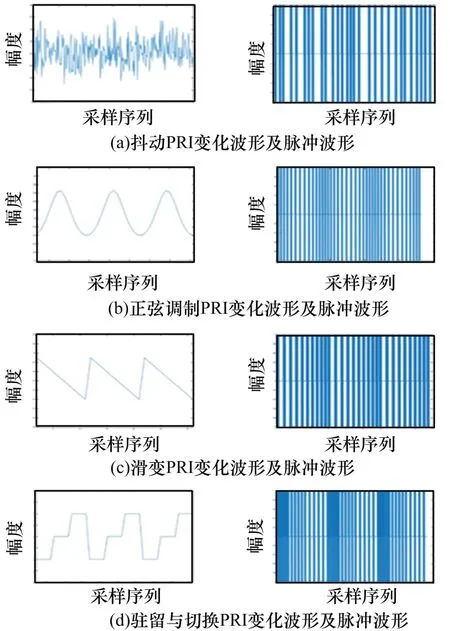
图5 驻留与切换PRI变化波形及脉冲波形

Matlab仿真产生上述4种不同PRI调制的信号，通过产生1～4的随机数，在上述的4种信号中循环产生10 000个随机信号，前9 000作为网络的训练数据，9 000～10 000作为网络的测试数据。4种信号的参数分别都有设置合理的变化范围，在合理的范围内通过随机选择来设置参数。

数据处理时，以中频数据作为一个样本进行训练和测试，由于数据维度的不一致和数量不均衡等问题，为了提高数据质量，本文对数据进行了预处理，对于维度不一致问题，通过等点数采样，本文实验中设定采样点数为M=1 000，即所有样本长度即为1 000点。

3.2 模型和参数比较

在深度自编码器中，本文抛弃了自编码器的重构层，整个网络的结构由输入层、隐藏层、输出层构成，每一层隐藏层都是对原始数据进行特征变换，整个网络的训练逐层进行，通过改变自编码器个数从而影响网络的特征提取性能，因为在每个自编码器训练结束后抛弃了自编码器的重构层，并以该自编码器的输出作为下一个自编码器的输入，所以在网络的最终架构上，自编码器的个数体现在隐藏层的个数。

本实验主要验证了DAE模型的特征提取和分类识别性能，并分析了不同网络层数和不同的batch-size对最终识别效果的影响。实验设计了网络层数为7、8、9、10、11层，batch-size从25、50到100的不同网络参数的分类识别实验。实验结果如表1所示。

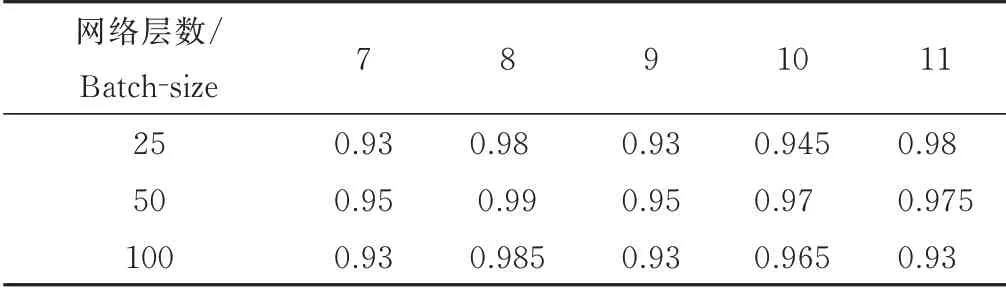
表1 网络参数设计

可以看到，在网络层数为8层（输入层，6层隐藏层，输出层），batch-size为50时，网络识别效果最好。

无监督逐层贪心预训练只是在一定程度上解决了局部最小问题[13]，随着隐含层个数、神经元数量和数据复杂程度的增加，梯度稀释越发严重，现有方法依然不能遏制局部最小。基于梯度理论的随机初始果，使DAE不能拟合一些高维复杂函数，但没有文献指出其原因。

3.3 实验结果分析和比较

3.3.1 仿真实验1

在数据输入网络前，对数据进行了预处理，通过对原始序列、滤波后序列、最终采样后序列分别进行数据集产生和网络识别后可得到对比结果，如表2所示。

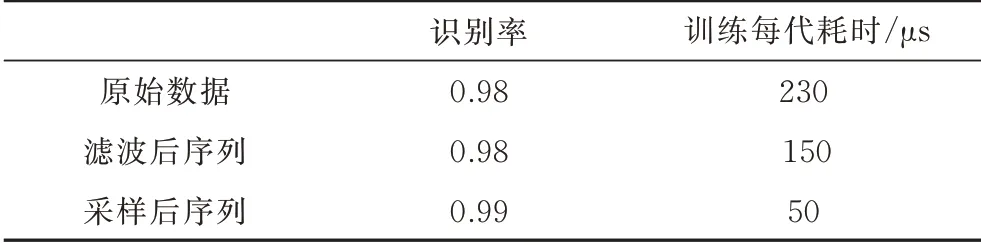
表2 实验结果对比

从表2可以看出经过预处理后的数据在保证识别率的同时大幅度降低了训练所需时间，可以证明本文所提到的预处理在降低数据维度的同时没有损失任何有助于识别的特征。

3.3.2 仿真实验2

研究算法在脉冲丢失下的识别正确率。本文取脉冲丢失率从1%步进至25%。文献[14]提出了一种特征提取法来区分4种复杂PRI调制样式。通过仿真发现，上述特征提取法虽然对复杂PRI调制样式能够较好识别，但是在脉冲序列样本较少以及脉冲丢失严重的情况下，其识别正确率却不理想。

图6表明2种算法在脉冲丢失的情况下对4种PRI调制样式识别的准确率对比情况。结果表明，本文算法的识别正确率明显要优于文献[14]中的算法。本文的识别正确率始终保持在95%以上，而文献[14]算法的识别正确率最低已经降到80%。从图6中还可以看到，随着脉冲丢失率的增加，文献[14]与本文识别正确率的差距越来越大，本文优势更加明显。

图6 不同脉冲丢失率下2种算法对比

本文对PRI调制方式的识别不需要对脉冲序列的先验知识，不需要从原始数据中提取特征，所以在脉冲数较少和脉冲丢失的情况下，识别率也保持稳定。

比较而言，基于深度学习的PRI调制方式识别具有更高的识别率，但是传统方法在模型的可解释性上优于基于深度学习的方法。

实验现象结合深度学习理论表明，基于深度学习的PRI调制方式识别的应用上应有如下限制条件:

1）模型遵循的假设是训练数据和测试数据是服从同一个分布。因此，测试数据要同训练数据基本特性相同，才能保证模型的普适性。

2）数据预处理是必须的环节。雷达对抗数据是复杂电磁环境下的非配合数据，存在严重的混叠、交错、不完整等情况，同时截获装备的差异导致精度、数据维度、采样率也不尽相同，因此通过数据预处理对数据做整齐统一化处理非常关键。

4 结束语

与传统的TOA统计直方图的方法不同，本文提出一种基于深度自编码器的PRI调制方式识别，DAE网络利用其无监督学习的模式提取了不同PRI调制序列的抽象深层次特征。实验表明，基于深度自编码器的PRI调制方式识别取得了很好的分类效果。另外，结合PRI调制序列的特点，通过滤波器思想对其进行了特征明显化处理，通过等点数采样实现了数据降维和归一化，对分类识别效果有了进一步的保证。