汽车车门有限元分析及可靠性优化设计

陈东，杨万庆，钱银超，刘向征

(广州汽车集团股份有限公司汽车工程研究院，广东广州 511434)

0 引言

汽车车门其主要功能是为乘客提供进出通道，因此需要经受反复的开关冲击应力，造成了局部位置出现疲劳开裂问题[1]。车门的开闭耐久周期较长，试验成本较高，因此车门的前期仿真很重要。冯长凯等[2]采用Ncode软件对车门进行疲劳分析，并通过试验验证，最终优化风险位置解决开闭耐久问题。乔淑平等[3]考虑了车门关闭及车门过开工况的影响因素。刑志伟等[4]基于某微型客车车门利用仿真方法预测开裂的风险点，然后通过试验验证方法的有效性。

由于开闭耐久的复杂性，往往仿真精度较低。究其原因，仿真趋于理论解，并没有充分考虑产品样件的实际制造和试验相关不确定因素的影响。本文作者以某次开闭耐久试验中开裂为例进行研究，首先利用Miner损伤理论对风险位置进行预测，然后将有限元法和试验设计相结合对结构进行最优化设计，最后充分考虑制造等不确定因素的影响，提升设计的可靠性，规避疲劳耐久开裂风险。把其可靠度从46.6%提升到95%，并通过试验证明可靠性优化设计方法可以有效降低车门开裂问题。文中研究为提前规避耐久开裂问题提供了一种可靠性设计思路。

1 车门的分析理论及流程

开闭耐久仿真分析的流程是，首先通过仿真计算得到危险点处的应力，然后对风险应力和应变进行线性损伤累计，最终计算出疲劳。其风险点处的应变-寿命关系方程式为

(1)

开闭耐久仿真的理论基础是线性损伤Miner理论[5]，其数学表达式为

(2)

式中:σ1，σ2，…，σl代表不同等级应力水平构成;N1，N2，…，Nl依次为各应力水平下的寿命水平;n1，n2，…，nl依次为各应力水平下的损伤;D为总损伤。

2 车门的有限元分析

2.1 车门有限元模型

文中的车门有限元分析模型，基本单元尺寸为10 mm，板壳基本采用壳单元Shell，焊点采用B31单元模拟，焊缝采用RBE2单元模拟。整个模型包括车门钣金、白车身、车门附件等。按照车门的实际质量进行配重，最终建立的有限元模型如图1所示，整个模型共有254 321个节点，226 635个单元组成。

图1 车门仿真分析模型

为了保证仿真模型的精确度，对车门进行刚度、模态和试验标定[6]。通过修正仿真建模，其最终的仿真和试验的刚度偏差对比见表1。通过表1结果基本验证了模型的精确度。

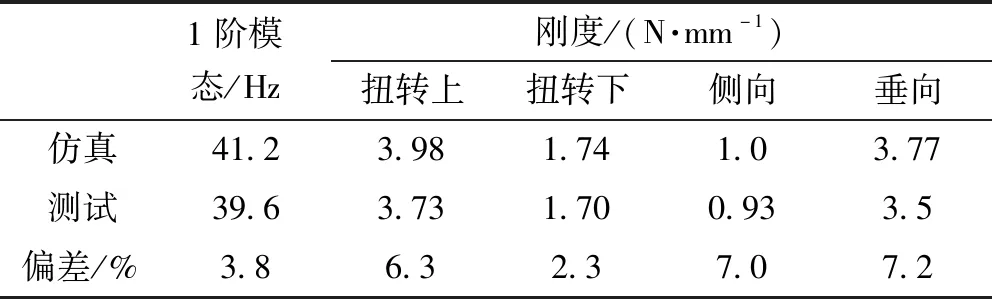
表1 仿真和试验的刚度偏差对比

2.2 车门冲击疲劳分析

2.2.1 冲击应力分析

利用Ncode软件对车门进行冲击耐久分析，其边界条件为约束车身截取端的全部6个自由度，对整车门开启3°～5°，对车门施加1.8 rad/s的初始角速度，其等效到门锁扣处为1.5 rad/s，同时对模型施加重力场。利用ABAQUS仿真软件计算出开闭耐久过程中的风险应力[7]。

应力最大处为车门窗框处单元在0.048、0.09 s处出现最大应力如图2所示。

图2 车门关闭时风险单元89 452

2.2.2 疲劳分析

利用Ncode疲劳分析软件对车门冲击应力进行疲劳分析，分别计算出全开、半开、全闭3种状态下的应力。然后对3种应力按照6∶3∶1进行组合，利用线性损伤原理计算的结果云图如图3所示。

图3 车门开闭耐久分析结果

经过对车门开闭耐久仿真分析，其风险最大处发生在窗框区域位置，该位置应力也最大，其寿命为6.3万次。当前车门不满足10万次寿命要求，需要进一步优化。

3 车门可靠性优化设计

3.1 优化设计概述

对车门进行优化设计，优化设计的核心就是把设计的问题通过数学模型来解决，即在约束条件下，求出数值最优解。优化分析的三要素即设计变量、设计目标以及设计约束[8]。

3.2 可靠性优化设计的数学表达式

经上述分析车门门框处焊点疲劳耐久分析不满足耐久寿命要求，故对其进行优化分析其数学模型[9]为：

Find：{(x1,ρ1),(x2,ρ2),…，(xn,ρn)}T

(1)

Minimize：f(y)=f(x)+f(ρ)

(2)

(3)

式中:xi,ρi为优化设计变量；Y(ρ)为优化变量；C(yi)、D(yi)为设计约束函数；f(y)为目标函数。

3.3 可靠性最优设计

可靠性最优化设计参数如图4所示。

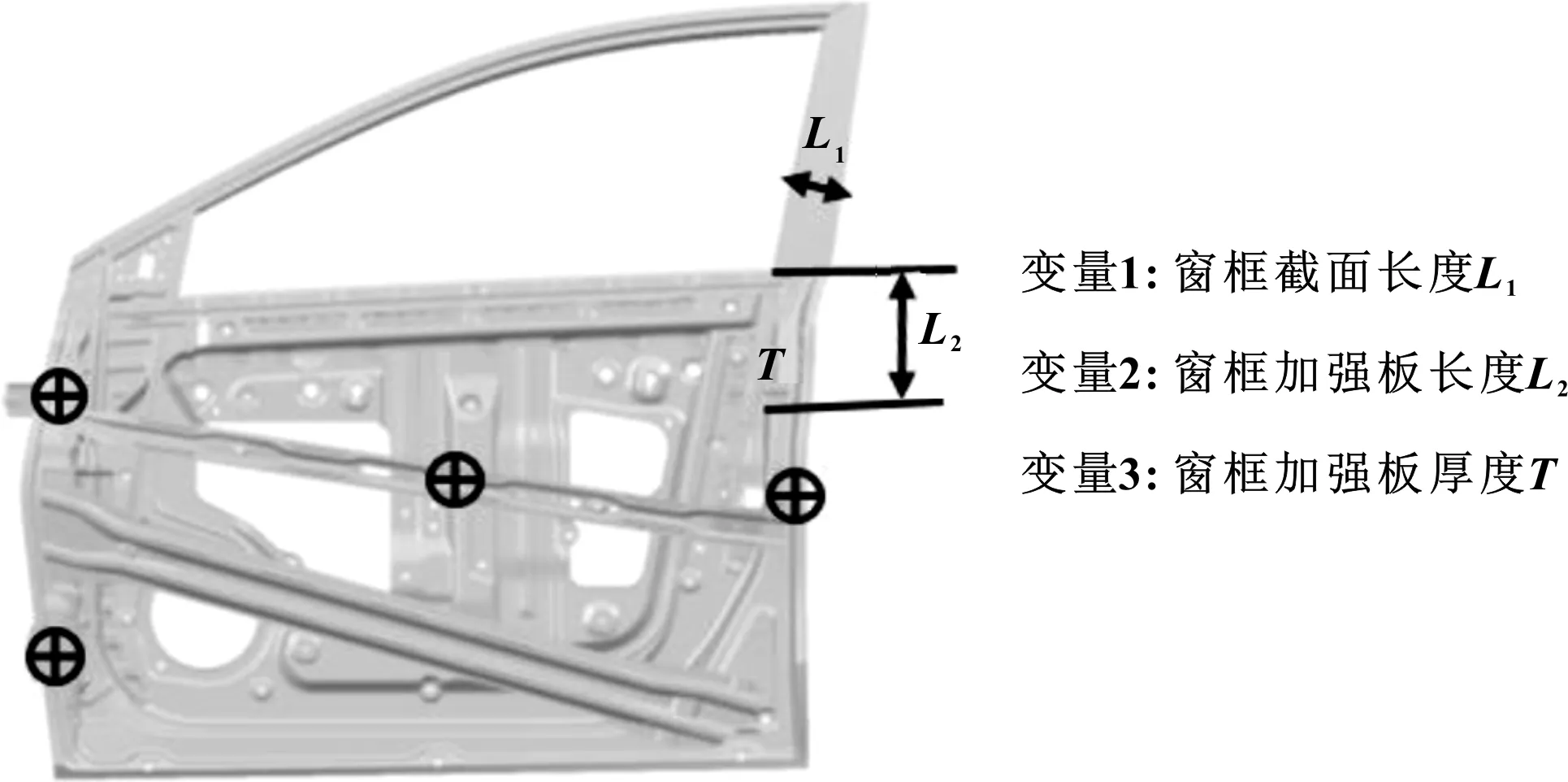
图4 优化参数

(1)优化设计参数主要包括窗框截面长度L1、窗框加强板长度L2和窗框加强板厚度T;

(2)设计约束定义垂向、侧向、扭转、模态可略低原始值10%，但需要满足目标值；开闭耐久寿命，不低于10万次；

(3)优化目标定义质量最轻。

运用Optimus软件采用拉丁超立方方法对设计变量进行抽样，设计变量组数为100组数据，利用软件得到其响应面，然后进行最优化设计，确定设计的最优值。最后对其最优设计方案加入其制造的波动性等不确定因素，如图5所示。最后进行MonteCarlo分析方法可靠性评估，得出其可靠性设计水平，可靠性设计流程如图6所示[10]。

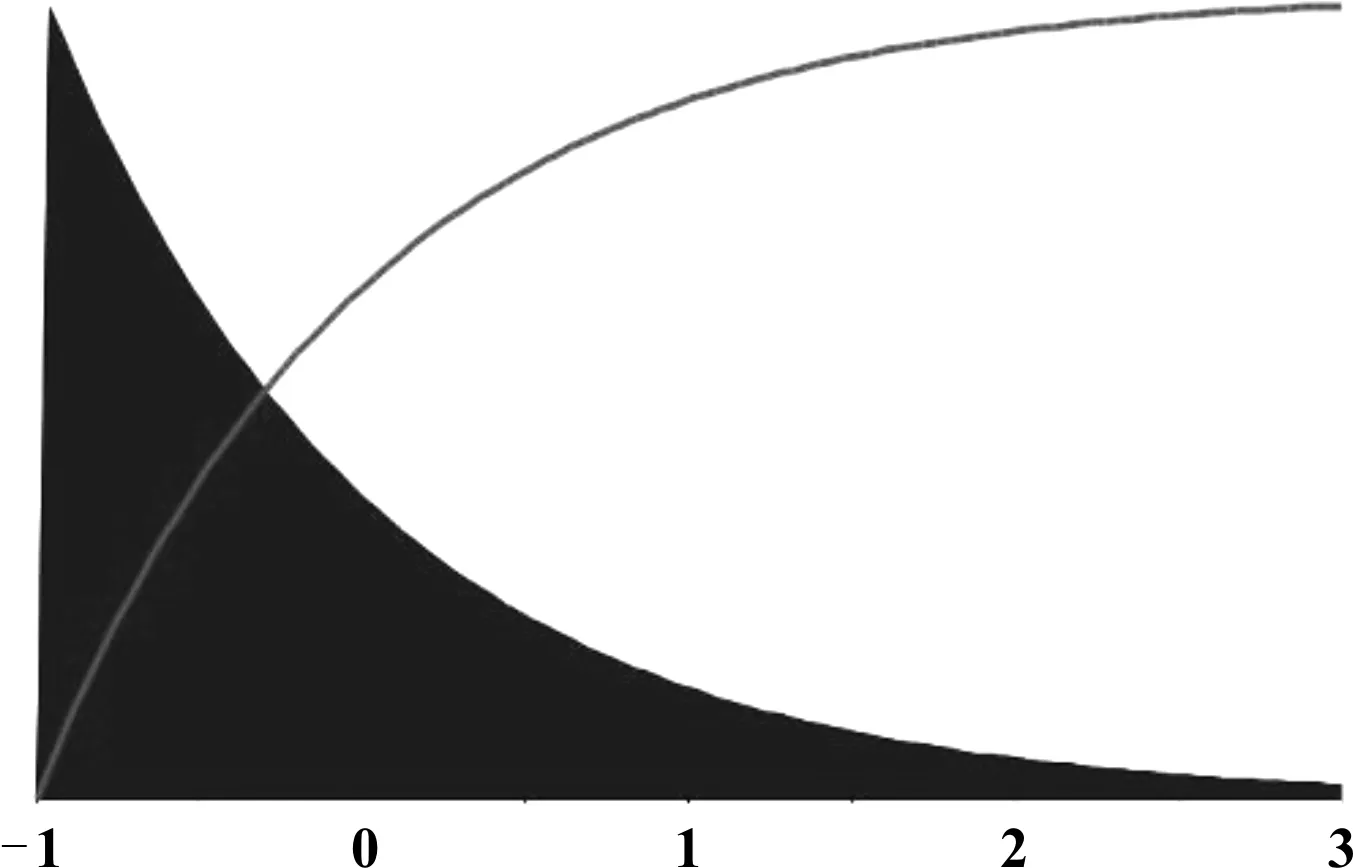
图5 制造参数的Weibull分布

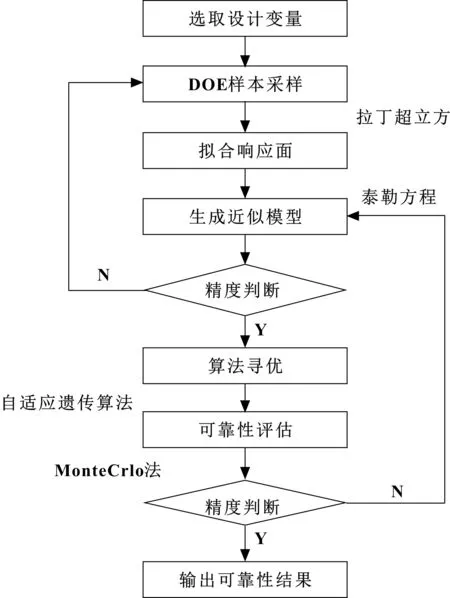
图6 可靠性设计流程

可靠性前后设计参数及设计目标变化见表2。

表2 优化前后性能对比

通过可靠性优化前后可靠度由46.6%提升到95%，新的可靠性设计质量基本和原来相当。优化后的开闭耐久置信度分布如图7所示(灰色为失效样本分布)。

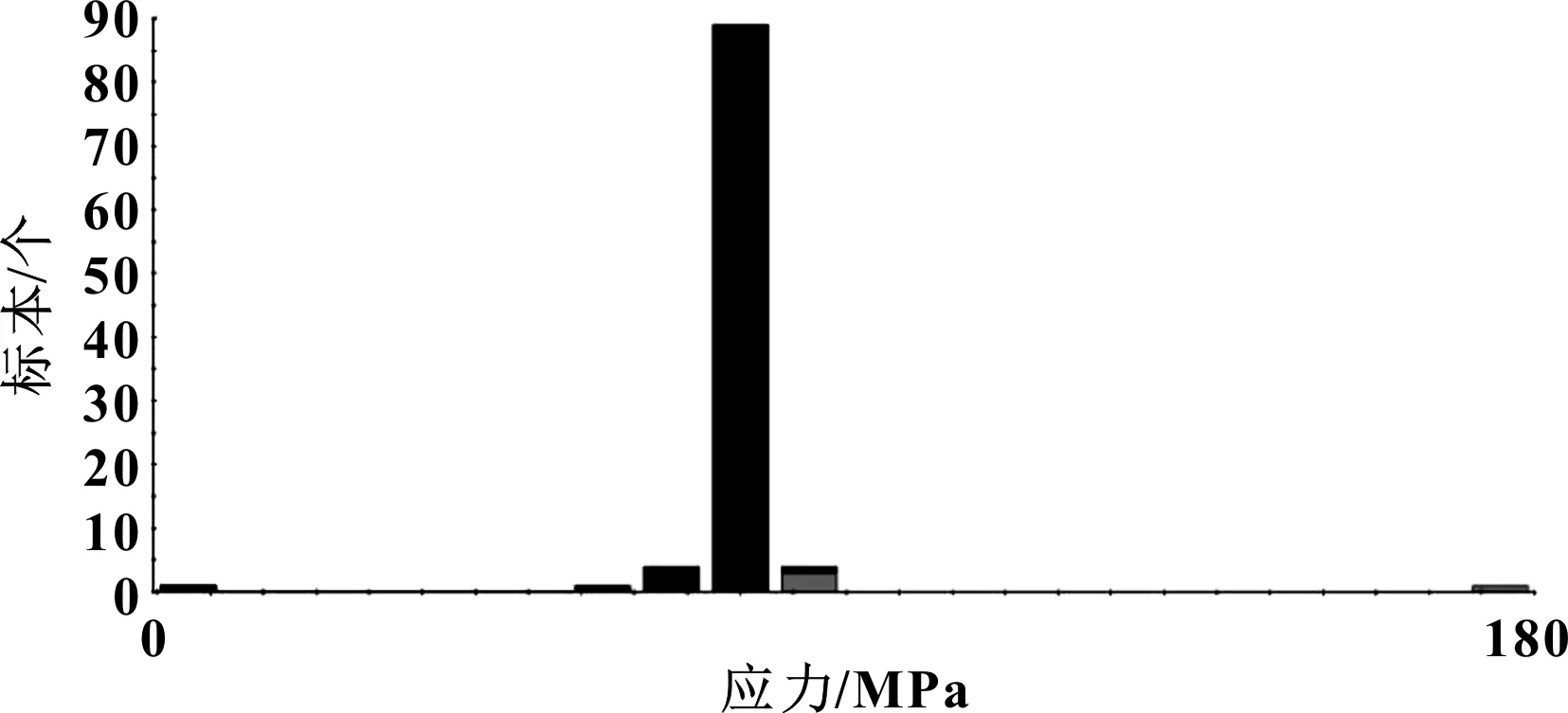
图7 可靠性优化后的样本分布

4 车门开关耐久试验验证

为了验证方法的合理性，优化前和可靠性优化后的车门分别取5对车门进行可靠性验证，对试验过程进行严格监控，每隔5 000次进行探伤。原方案在试验进行到5.2万次左右两侧车门均出现不同程度车门门框焊点开裂，如图8所示。开裂的位置基本和仿真一致。利用可靠设计后的车门其未出现开裂问题，进一步验证方法的合理性。

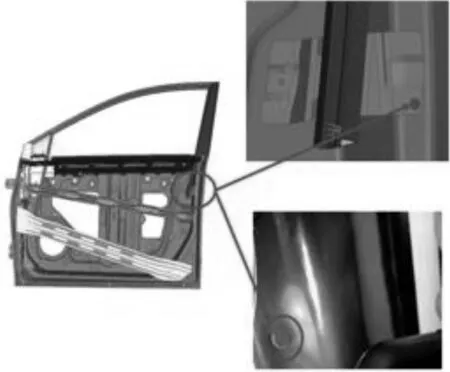
图8 车门窗框开闭耐久失效图

5 结论

(1)文中的研究首先通过对车门开闭耐久性能进行有限元分析，然后将有限元法和试验设计相结合对结构进行最优化设计，最后充分考虑制造等不确定因素的影响，提升设计的可靠性，降低疲劳耐久开裂风险。

(2)结果表明，充分考虑制造等不确定因素的波动性的可靠性设计方法能对提升车门耐久水平，有一定的帮助作用。

(3)文中的研究把某车门可靠度从46.6%提升到95%，并通过试验验证，证明方法的合理性。所得结论对车门可靠性设计具有一定的借鉴意义。

(4)由于可靠度对标需要大量的样本，文中研究数据量有限存在一定偏差。