将军饮马

赵璐璐

今天，爸爸和我讲起了“将军饮马”的故事。

为了能让大家听明白，我先给大家普及一下对称点的概念。

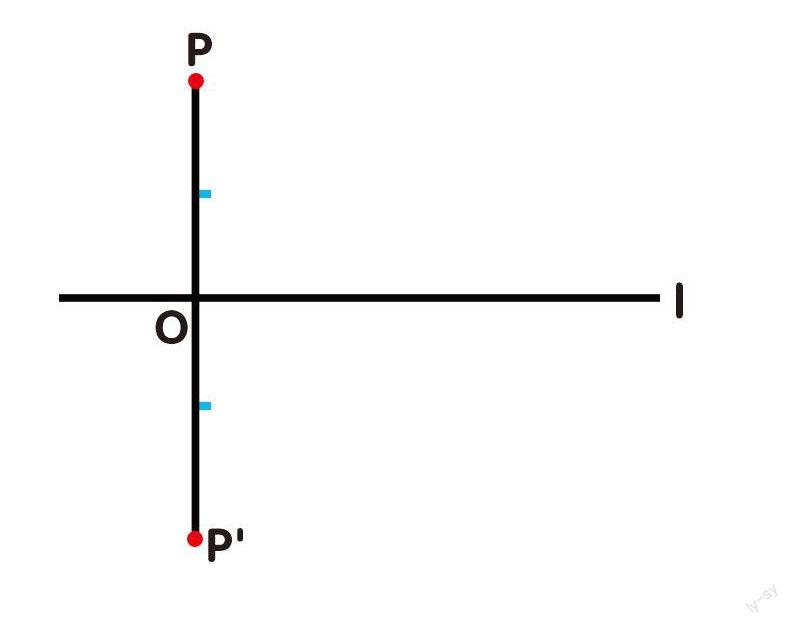
已知一条直线I和直线外一点P，求P点关于直线I的对称点P'。

如左下图，由P点向I引垂线，垂足为O，延长PO至P'，使OP'=OP，则P'即为所求。

爸爸说：“在古罗马的亚历山大城有一位精通数学和物理的学者，名叫海伦，他聪明过人。有一天，一位将军专程去拜访他，向他请教一个百思不得其解的问题。

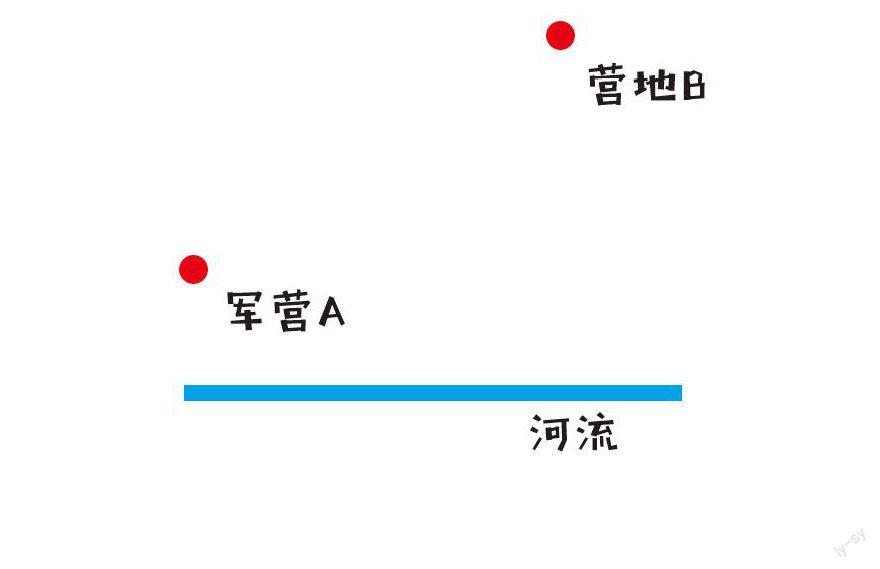
“将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的B地开会，应该怎样走才能使路程最短？如何确定饮马的地点？从此，这个被称为‘将军饮马的问题广泛流传。这个问题并不难，据说海伦略加思索就解决了它。”

我迅速地想出了至少两种答案，但爸爸都摇了摇头。

爸爸接着说：“海伦的方法是这样的，如下图，从A出发向河岸引垂线，垂足为D，在AD的延长线上，取A关于河岸的对称点A'，连接A'B，与河岸线相交于C，则C点就是饮马的地方，将军只要从A出发，沿直线走到C，饮马之后，再由C沿直线走到B，所走的路程就是最短的。

“如果将军在河边的另外任一点C'饮马，所走的路程就是AC'+C'B，但是，AC'+C'B=A'C'+C'B>A'B=A'C+CB=AC+CB.

“可见，在C点外任何一点C'饮马，所走的路程都要远一些。海伦的方法是不是很巧妙？”

我赶紧又拿出课本，查找起对称图形问题，课本上没有这样的专题讲解，看来需要靠自己查资料总结了。原来，对称问题分为两种，一种是轴对称，一种是中心对称。

相信大家对蜻蜓和蝴蝶都不陌生，仔细观察一下，这两种昆虫都是对称的。也就是说，以这两种昆虫身体的中心线为轴，把左右兩部分重叠在一起，你会发现这两部分会完全重合。在几何图形中也有不少轴对称图形，比如，等腰三角形、等腰梯形、圆……

还有一种图形叫“中心对称图形”，这种图形都有一个对称中心。典型的是圆形，圆心就是它的对称中心，此外还有平行四边形等。