一种优化的频率驾驭算法研究

赵书红 董绍武*③④ 白杉杉 高 喆

①(中国科学院国家授时中心 西安710600)

②(中国科学院时间频率基准重点实验室 西安 710600)

③(中国科学院大学 北京100049)

④(中国科学院大学天文与空间科学学院 北京100049)

1 引言

时间是一个国家科技、经济、军事和社会生活中至关重要的参量，其应用范围从基础研究(相对论验证、基础物理常数测量等)，渗透到工程技术应用领域(导航定位、深空探测等)。特别在现代高科技领域和国防建设中，如全球卫星导航系统(Global Navigation Satellite System,GNSS)、现代军事通信系统、航空航天系统等，高精度、稳定可靠的时间更是其未来技术迅速发展的核心要素。

目前国际标准时间是协调世界时(Coordinated Universal Time,UTC)，由国际权度局(International Bureau of Weights and Measures,BIPM)以Circular T公报形式发布。但UTC是“纸面时间”，滞后40～45 d，不满足用户对高精度时间信号的实时性要求，因此各守时实验室需要独立产生和保持一个稳定的标准时间系统UTC(k)，即UTC在本地的物理实现[1]。目前，全球多数时间实验室利用一定数量的原子钟(氢钟、铯钟等)联合计算得到地方原子时尺度TA(k)，即“纸面时间”。以TA(k)作为驾驭参考，采用最小二乘估计方法预测待驾驭原子钟的频率，使其尽可能接近或符合纸面时间尺度的频率，依据该值对原子钟进行频率驾驭，最终实现实时物理信号UTC(k)的输出[2]。

实时物理信号UTC(k)产生的过程中，往往会有各种各样的随机因素存在，比如观测噪声、设备噪声以及外部干扰等，同时这些随机因素也是随时间而变化的，但最小二乘估计方法没有很好消除噪声影响，且易受异常数据和异常信号的影响，因此现有的频率驾驭算法还有改进的空间。自适应的控制方法是基于运行期间的测量值来改变增益矩阵，而不再是依据经验来选择，可以更好地控制系统达到期望的目标，因此本文采用基于自适应的控制方法，即最优二次型高斯控制算法(Linear Quadratic Gaussian control,LQG)，利用最小化二次代价函数不断地逼近最优控制。再通过Kalman滤波方法，构造增益矩阵的递推公式，将控制值和滤波器不断迭代直至收敛，最终得到最优滤波器[3]。

本文提出了一种优化的频率驾驭算法，主要分为纸面时间计算和实际物理信号实现两个部分。第1步，基于实时的原子钟数据和BIPM公布的Circular T公报的数据，采用ALGOS算法，产生一组氢铯联合时间尺度，发挥了氢钟和铯钟的特性，保证驾驭参考的准确性和实时性。第2步，通过调整最优二次型高斯控制算法中的参数，使得代价函数最小化，再利用Kalman算法计算最优的氢钟频率驾驭量输送至频率调整设备中，保证输出的实时物理信号性能，整个驾驭过程是优化、闭环的。基于我国时间基准保持系统，对一台氢钟进行了为期140 d的频率驾驭试验，分别在氢铯联合时间尺度算法、LQG算法参数选择以及优化的频率驾驭算法等方面开展试验，分析试验结果，验证了该算法的有效性。

2 基本原理

2.1 ALGOS算法

BIPM提出了ALGOS算法，目的是通过收集全世界时间实验室的原子钟数据，产生一个稳定的自由原子时(Échelle Atomique Libre,EAL)，并利用多台基准频标的频率(进行广义相对论和黑体辐射改正后)的加权平均，对EAL的频率进行驾驭得到既稳定又准确的时间尺度——国际原子时(International Atomic Time,TAI)。

若有N台原子钟，其读数为hi(t)，i=1,2,···,N，利用加权平均算法，建立一个时间尺度TA(t)。ALGOS算法的基本公式如式(1)所示[4,5]

其中，Wmax表示最大权，A为需多考虑参与计算的原子钟的性能的参数。

2.2 实际物理信号实现算法

实际物理信号实现算法是Kalman算法和LQG算法的综合，本节重点介绍Kalman算法、LQG算法原理和实际物理信号实现算法流程。

2.2.1 Kalman算法

Kalman算法的状态方程，如果假设为线性微分方程，仅描述了自由运转的原子钟模型，与频率驾驭量的实际应用情况不符，因此状态模型不能简单用线性微分方程表示，必须增加控制项b(τ)u(t k)[6–8]。

含有控制量的状态方程描述为

其中，X为原子钟相位和频率的状态向量，t k为离散时间，τ=t k+1−t k为时间间隔，ϕ(τ)为状态转移矩阵，b(τ)为 传播项，u(t k)为tk时刻的频率驾驭值，w(t k)是 原子钟噪声，在时域上互不相关，w(t k)～N(0,Q(τ))。

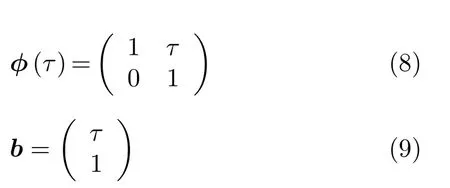
原子钟的状态方程仅考虑原子钟本身的噪声，不考虑测量过程中引入的噪声。测量矩阵h描述系统测量过程，即描述待驾驭原子钟与TA的相位偏差过程，并且测量噪声v(t k)～N(0,R(t k))。Kalman算法的测量方程为

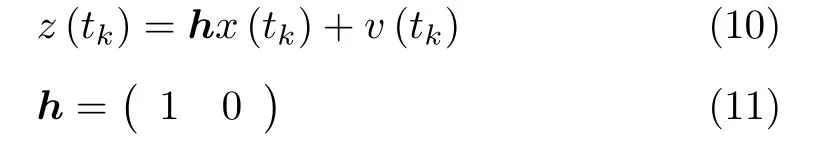
2.2.2最优二次型高斯控制算法

最优二次型高斯控制算法(LQG算法)是一种较为灵活的算法，通过调整WQ和WR参数值，优化频率驾驭值。为保证LQG算法计算获得最优的主钟频率驾驭值，必须保证代价函数J最小[9–11]。

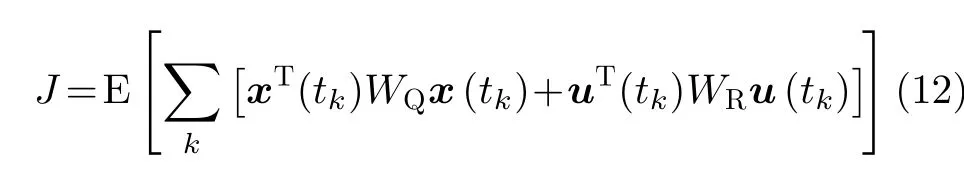
2.2.3物理信号实现算法流程

物理信号实现算法包括预测和修正步骤。在预测步骤中，利用Kalman状态方程确定下一时刻的估计。在修正步骤中，使用最新测量值修正模型预测的偏差[14,15]。

预测：

3 优化的频率驾驭算法

优化的驾驭方法通过寻找驾驭函数u(t)，在满足状态方程式(7)和测量方程式(10)的条件下，使得代价函数J达到最小。针对实时物理信号UTC(k)产生的随机控制问题，其全局最优频率驾驭函数的确定是比较困难的。利用LQG算法使得最小化二次代价函数不断地逼近最优控制，再通过Kalman滤波方法，构造增益矩阵的递推公式，将控制值和滤波器不断迭代直至收敛，最终得到最优滤波器。该算法可以很好地降低各种类型噪声对系统的影响，并在最短时间可以消除异常值对频率驾驭的影响，最终提高频率驾驭后信号的稳定性和系统的可靠性。

优化的频率驾驭算法分为纸面时间和实际物理信号实现两个部分。纸面时间实现算法，基于氢原子钟和铯原子钟的原子钟数据，采用ALGOS算法产生一个准确、稳定的纸面时间TA(k)，该纸面时间尺度的稳定度优于任何一台原子钟的稳定度。物理信号实现算法，以氢钟与纸面时间TA(k)的相位偏差数据作为一组输入数据，考虑到氢钟的外部频率驾驭操作，综合Kalman算法和LQG算法计算主钟的频率驾驭量，将该值输送至相位微调器中，最终实现物理信号输出。该物理信号作为本地原子钟数据采集的输入信号，参与纸面时间计算，循环往复，整个过程是闭环的。氢钟的频率驾驭过程如图1所示，图中MC为氢钟经频率驾驭后的输出信号。

4 测试及分析评估

4.1 氢铯联合时间尺度TA产生

利用我国时间基准系统的原子钟测量比对系统，选择2019年1月1日(修正的儒略日期(Modified Julian Date,MJD)=58484)至2019年5月23日(MJD=58623)的原子钟比对数据，采用在线连续运行的20台原子钟(13台铯钟和7台氢钟)与标准时间UTC(NTSC)的相位比对数据，采样间隔为1 h。经钟差预测、频率预报以及权重估计等，利用ALGOS算法，计算得到纸面时间尺度TA。

由于环境异常或设备故障等因素，可能造成原子钟比对数据中出现缺失、异常数据等现象。为保障纸面时间尺度的准确性和连续性，必须对原始的原子钟数据进行数据预处理，试验中选用滑动的3σ粗差剔除法和三次样条插值方法解决异常数据和缺失数据。

数据预处理后，基于ALGOS方法，利用7台氢原子钟，产生一个氢原子钟组成的时间尺度TAHM。同时又利用13台铯原子钟组以及经过TAI速率校正后综合产生的原子时尺度TACs。这两个时间尺度互为参考，利用TAHM来减小铯原子钟的短期波动，而利用TACs来修正TAHM的长期漂移，综合两者得到稳定度和准确度最优的时间尺度TA。由于参与计算的原子钟数据为实时的，且计算前后的时间尺度经过链接，因此最终计算获得的时间尺度TA是连续且实时的[16,17]。

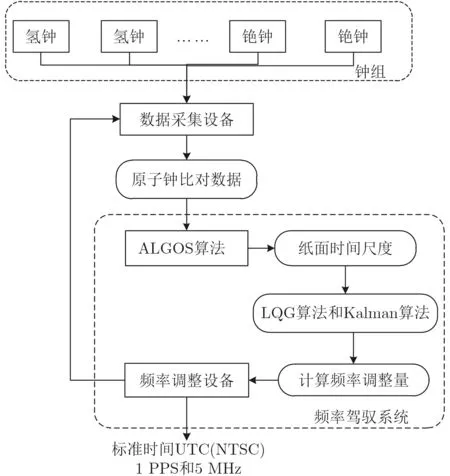
图1 氢钟的频率驾驭框图

从图2可以看出，氢铯联合时间尺度TA与标准时间UTC(NTSC)的相位偏差保持在±5 ns以内，对比国际标准时间UTC与标准时间UTC(NTSC)的结果(数据来源于BIPM的Circular T公报)，两组结果基本吻合。从图3可以看出，氢铯联合时间尺度TA与UTC的相位偏差均值为–0.38 ns，均方根误差(Root Mean Square,RMS)为0.78 ns，并且30 d稳定度达到4.7×10–16[18,19]，因此氢铯联合时间尺度TA是一个准确可靠的驾驭参考。

4.2 实时物理信号产生

4.2.1 LQG算法的参数确定

LQG算法通过调整WQ和WR参数，可以计算获得最优的主钟频率驾驭量，其中WQ是具有两个非零对角线的2×2矩阵，有两个可变参数，WR是1维可变参数。给定WQ和WR参数，利用2.2.2节中式(12)、式(13)，可以计算出LQG算法的增益Gˆ0,Gˆ0=(g x,g y)，其中gx为 相位增益，gy为频率增益。

图4(a)和图4(b)分别显示了WR=109,WQ的两个参数选择范围从(10–14,1014)取值时，相位增益g x和频率增益gy的3维曲面图。从图中可以看出，当gx和gy取值接近零值时，随着WR的增大，WQ(1,1)和WQ(2,2)的取值范围变大。

WQ和WR参数选择可以利用式(20)，当函数值为0时，选取参数的最优值[12]。

图2 TA、UTC与UTC(NTSC)相位偏差结果

图3 TA相对于UTC的相位偏差以及稳定度结果

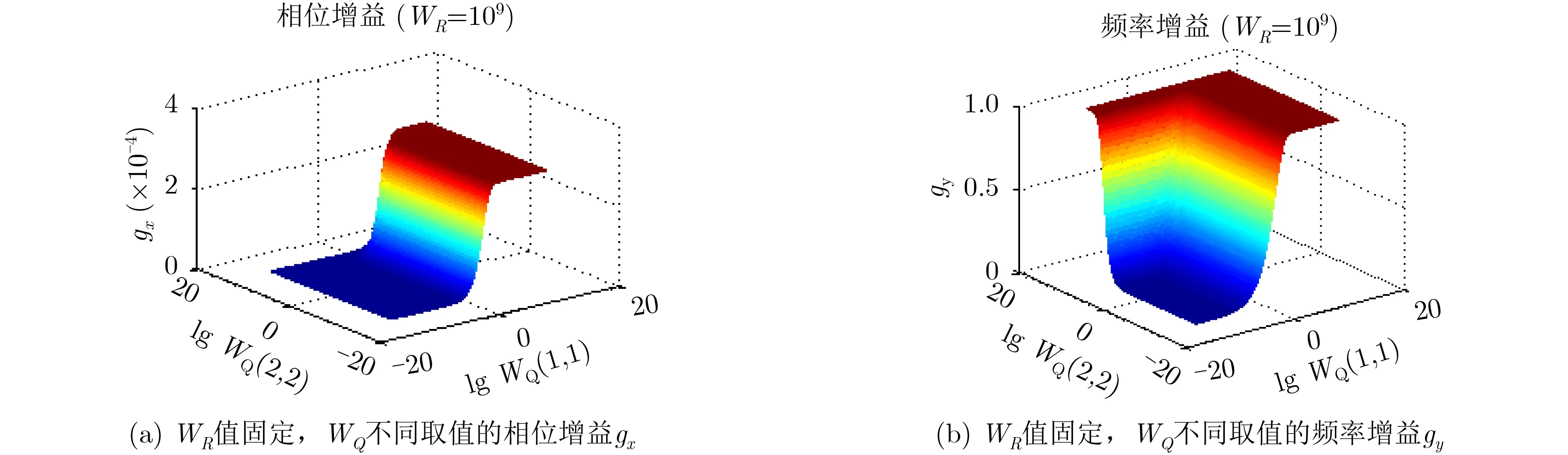
图4 WR值固定，WQ不同取值的增益

图5 WQ值固定，WR不同取值的函数f变化曲线

4.2.2最优频率驾驭量计算

图7中黑色虚线代表氢钟H067相较于纸面时间TA的相位偏差(扣除了二次趋势)，红色实线代表应用优化的频率驾驭算法后的输出信号与纸面时间TA的相位偏差。从图中可以看出，采用优化的频率驾驭算法，驾驭后信号一直稳定在零处。相比于优化的频率驾驭算法，采用最小二乘估计方法驾驭，扣除了二次趋势后，驾驭后的信号波动明显增大，由此表明优化的频率驾驭算法可以很好地实现原子钟的频率驾驭。

图6 氢原子钟的频率驾驭量

当时间间隔在100～10000 s时，氢钟噪声以频率白噪声为主；当时间间隔在10000 s～7 d时，氢钟噪声以频率闪烁噪声为主；从图8可以看出，利用优化的频率驾驭算法，有效地抑制了频率白噪声和频率闪烁噪声，同时很好地消除了氢钟的2次项趋势，使得驾驭后的信号与氢铯联合时间尺度TA的相位偏差控制在±1 ns以内，并提高了驾驭后信号的频率稳定度[20,21]。

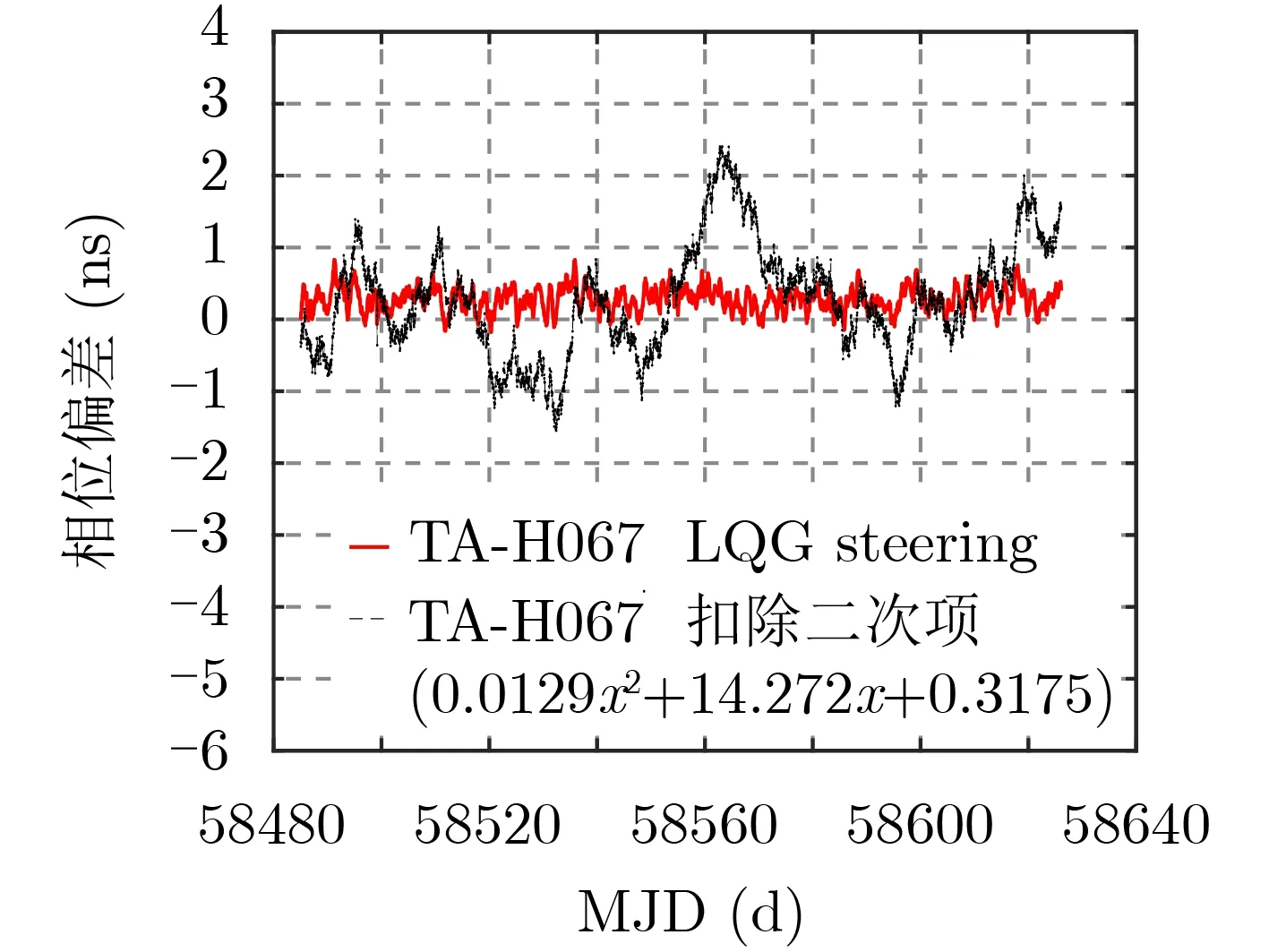
图7 采用优化的频率驾驭算法和最小二乘估计方法，驾驭后的输出信号与TA的结果分析

图8 采用优化的频率驾驭算法和最小二乘估计方法，驾驭后的输出信号与TA的稳定度结果

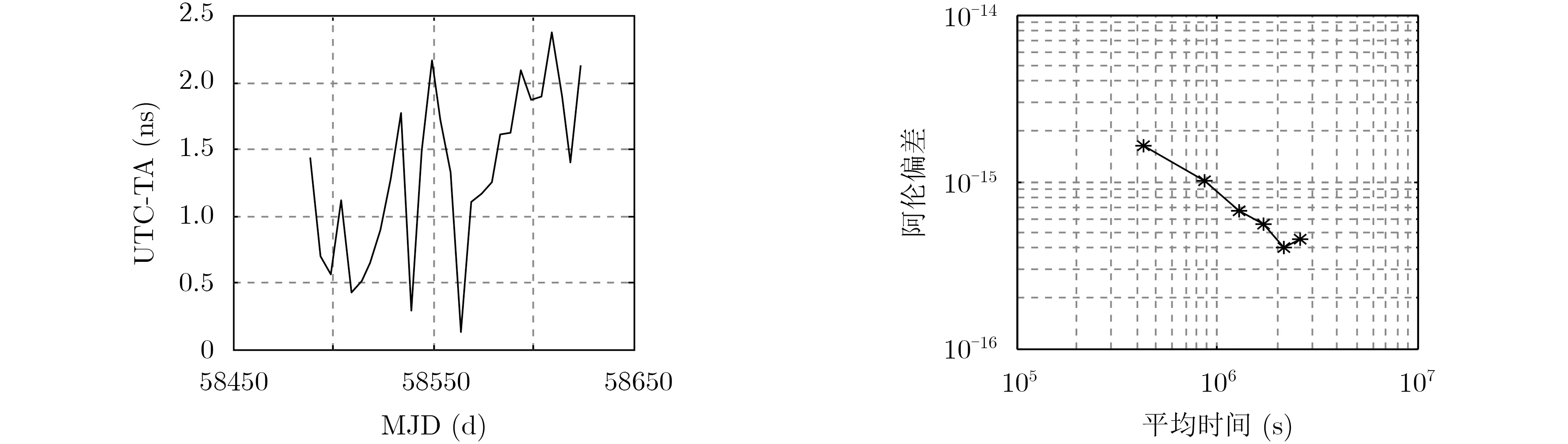
图9 采用优化的频率驾驭算法，驾驭后的输出信号与UTC的结果分析

利用国家授时中心的溯源链路，将驾驭后的时间信号溯源至国际标准时间UTC。从图9可以看出，驾驭后的实时物理信号与国际标准时间UTC相比，保持在±3 ns以内，且实时物理信号30 d的稳定度优于5×10–16[15]。图10中带圈虚线代表氢钟H067的稳定度，实线代表了纸面时间TA的稳定度，以及带框实线代表可驾驭后输出信号的稳定度。从图中可以看出，氢钟受频漂和随机游走噪声等的影响，频率稳定度随时间推移变差。多台原子钟综合计算获得的纸面时间尺度TA，很大程度上消除了频漂和随机游走噪声的影响，短期稳定度和长期稳定度相比于氢钟的稳定度均得到了提高。而应用优化的频率驾驭算法，驾驭输出后的物理信号稳定度与纸面时间TA的稳定度基本保持一致，驾驭后实时物理信号的稳定度优于氢钟的自身稳定度。

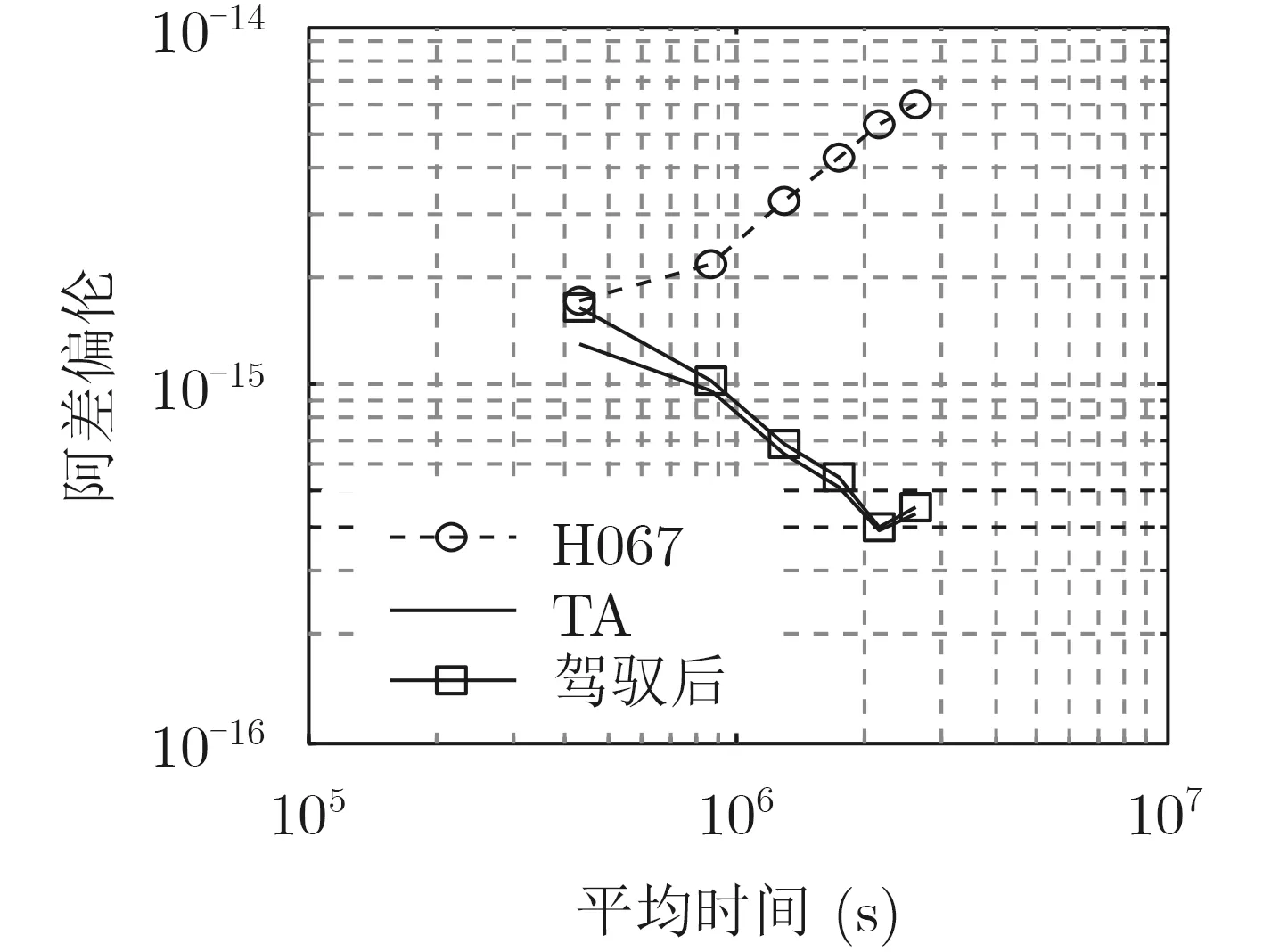
图10 以UTC作为参考，氢钟H067，纸面时间TA和驾驭后实时物理信号的稳定度结果

5 结束语

随着各领域对高精度时间的精度不断提高的要求，更高精度的时间产生技术的研究受到广泛的关注。频率驾驭算法作为高精度时间产生的重点研究问题，其算法的有效性取决于驾驭参考的时间尺度、最优驾驭量计算等方面。因此本文提出了一种优化的频率驾驭算法，综合ALGOS算法、Kalman算法和LQG算法，迭代计算出最优频率驾驭量，利用频率调整设备，最终实现高精度时间信号输出。

基于我国时间基准系统搭建了试验平台，利用优化的频率驾驭算法，对一台氢原子钟进行140 d的频率驾驭试验，试验结果说明，该算法可以提高输出实时物理信号的准确度和稳定度，驾驭输出的时间信号与国际标准时间UTC相比，相位偏差保持在±3 ns以内，且30 d稳定度优于5×10–16，为提高我国时间基准的性能提升奠定了基础。