陀螺定向中子午线收敛角的计算方法

中铁一局集团天津建设工程有限公司，天津 300000

1 子午线收敛角的概念

以真子午线为参考，坐标系纵轴X北端在其东侧时，子午线收敛角为正，反之则为负。地面上的点纬度B和中央子午线的距离经差ΔL决定了子午线收敛角的大小，计算其角值可以用如下近似计算公式：

在一个投影带内，高斯平面子午线收敛角的变化遵循一定规律。距离中央子午线越远，收敛角越大，在中央子午线上收敛角等于零；距离赤道线越远，收敛角越大，在赤道线上收敛角等于零。

2 坐标方位角的换算

陀螺仪北方向与真北方向间存在角度偏差，角度的偏差值就是陀螺仪的仪器常数，偏东为正、偏西为负。坐标北方向与真北方向间的角度偏差就是子午线收敛角，相对真北方向，坐标方位角偏东为正、偏西为负。陀螺北、真北、坐标北方向关系如图1所示。陀螺北、真北、坐标北方向之间的角度关系可用如下公式表示：

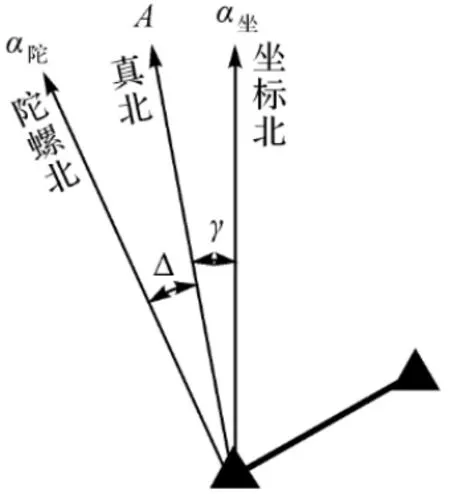
图1 陀螺北、真北、坐标北方向关系示意图

式中：A为真北方位角；Δ为仪器常数；γ为子午线收敛角。

由此可知计算子午线收敛角γ是推算坐标方位角的第一步，其计算精度直接影响陀螺推算坐标方位角的精度。

3 子午线收敛角的计算

子午线收敛角如图2所示，以真子午线为准，是真子午线与坐标纵线之间的夹角。坐标纵线东偏为正，西偏为负。

图2 子午线收敛角概述图

赫里斯托夫给出的展至第7次项的计算公式：

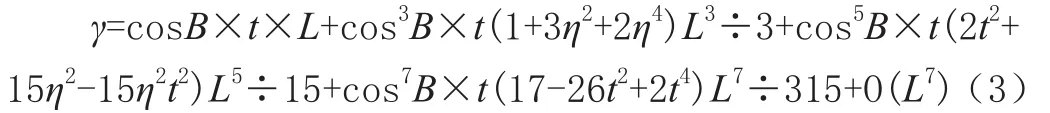
式中：t=tanB；η=e′×cos2B，e′为第二偏心率；B为纬度；L为经差。

《控制测量学》中展至第5次项的计算公式：

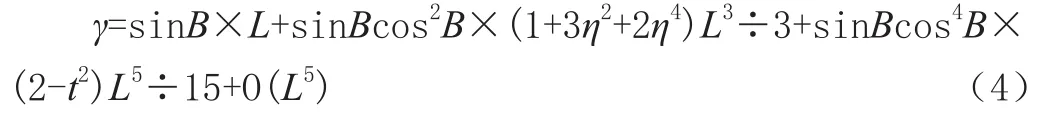
式中：t=tanB；η=e′×cos2B，e′为第二偏心率；B为纬度；L为经差。

《测量学》中的近似公式：

式中：γ为子午线收敛角；B为纬度；L为经差。

《工程测量学》中的近似公式：

式中：y为测站点的横坐标；N为卯酉圈曲率半径，；e为第一偏心率。

在工程测量中，常用子午线收敛角的计算公式如下：

式中：γ子午线收敛角，′；y为点的横坐标，km；K为系数。以纵坐标X（以km计）为引数，由子午线收敛角系数K值表中查取，子午线收敛角系数K值表如表1所示。

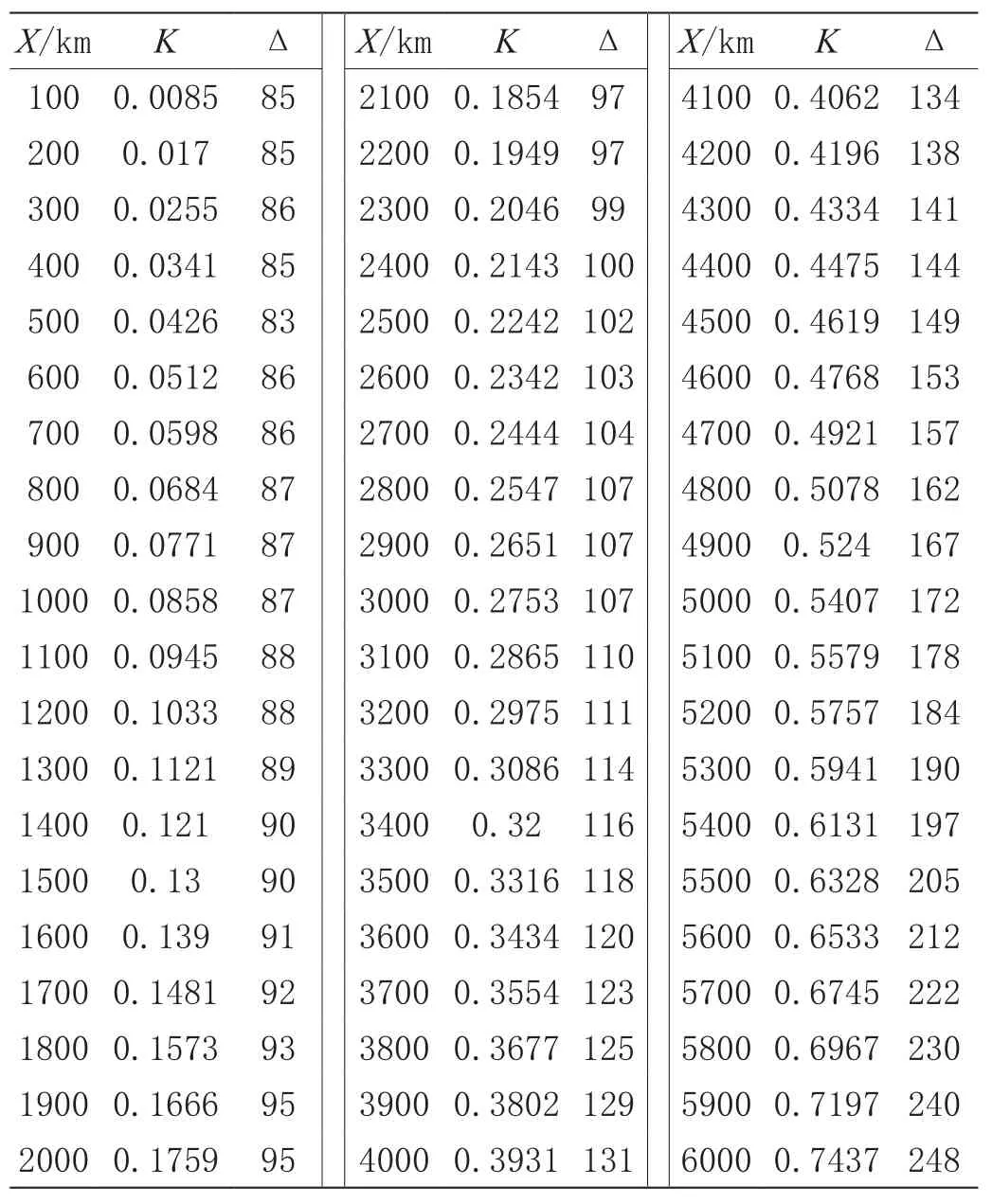
表1 子午线收敛角系数K值表

4 工程计算实例

以成都轨道交通17号线（一期）工程盾构区间为例，平面坐标系统采用工程坐标系统，WGS84椭球，中央子午线为104°04′，投影面为490m（成都高程）。大地坐标系WGS-84椭球参数：长半径a=6378137；短半径b=6356752.3142；扁率α=1/298.2572236；第一偏心率e=0.0818191908425523；第二偏心率e′=0.0820944379493946。根据椭球参数可知已知点数据，已知点列表如表2所示。利用各公式计算洞外已知点D1718和洞内检测已知点C1146的子午线收敛角，计算结果如表3所示。分别使用公式（5）和公式（7）所计算的子午线收敛角来计算陀螺仪仪器常数和陀螺推算方位角，结果如表4、表5所示。

表2 已知点列表

表3 子午线收敛角计算结果

表4 陀螺仪仪器常数计算表

表5 陀螺推算方位角与平面坐标方位角差值表

5 结论

计算结果表明，在成都轨道交通7号线（一期）工程施工中，利用已知点数据计算子午线收敛角采用公式（5）计算的结果精度能达到0.001″，采用公式（7）计算的结果精度达到2″，计算坐标方位角精度均在0.1″级，根据项目施工已知点数据采用公式（5）和公式（7）均可保证足够的计算精度。陀螺定向为隧道内平面控制网联测和开挖方向的正确性提供了检测复核依据，陀螺定向适用于地下工程定向测量，同时为今后的施工提供了指导。