进气条件对PEMFC动态响应的影响

2021-05-29李一鸣戴海峰

电池 2021年2期

李一鸣，戴海峰，袁浩

(1. 同济大学汽车学院，上海 201804； 2. 同济大学新能源汽车工程中心，上海 201804)

在实际应用中，伴随着车辆的启停和加减速，质子交换膜燃料电池(PEMFC)通常运行在变载工况下，容易出现水热管理不善、反应气体供应不足等问题。为更好地了解电池性能、延缓寿命衰减，有必要研究燃料电池的动态响应特性。

人们通过实验手段来观察燃料电池在不同工况下的动态响应特性。J.Hamelin等[1]以巴拉德MK5-E型燃料电池为研究对象，记录了多幅度连续变载工况下电压和电流的时域响应，测得电堆的响应时间不到0.15 s。S.Kim等[2-3]研究了反应气体过量系数、氢气浓度等对燃料电池动态性能的影响。G.B.Jung等[4]测试了不同进气条件下燃料电池的瞬态响应，认为动态变载下的不稳定响应与阴极氧气质量传输、膜电导率有关。受条件限制，燃料电池运行过程中膜含水量等内部参数的变化很难测得，为此，诸多学者采取模型仿真来研究燃料电池的动态响应特性。P.R.Pathapati等[5]通过建立动态数学模型，模拟电流突变时电堆的输出电压、温度、流道内压以及反应气体流速的动态响应。K.H.Loo等[6]借助一维两相PEMFC模型，预测燃料电池在不同变载幅度下的活化和欧姆过电势、液态水饱和度及膜含水量。这些研究可较全面地描述燃料电池的动态响应特性，但缺少对膜结合水具体分布的计算，且模型均假设膜结合水的吸附和脱附速率为无穷大，与实际情况不符。

本文作者用COMSOL软件建立PEMFC一维两相流模型，在上述研究的基础上考虑膜结合水有限速率的吸附和脱附过程，进一步研究负载阶跃变化时，燃料电池膜结合水分布以及反应气体浓度、输出电压等关键内外参数的动态响应，并分析不同外部进气条件对动态响应特性的影响。

1 数学模型

PEMFC通常由气体流道、气体扩散层、催化剂层和质子交换膜组成。仿真建立的一维两相流模型以膜电极组件(MEA)作为计算域，包含气体扩散层、催化剂层和质子交换膜，如图1所示。

图1 PEMFC的一维模型示意图Fig.1 Schematic diagram of one-dimensional model of PEMFC

1.1 燃料电池基本方程

1.1.1 电荷守恒

燃料电池内部的电荷传输过程可由式(1)～(2)描述：

Se=·(-σeφe)

(1)

Sp=·(-σpφp)

(2)

式(1)～(2)中：φe为固相电势；φp为膜相电势；σe为固相电导率；σp为膜电导率。电子电流源项Se和质子电流源项Sp的计算方法见式(3)：

(3)

电极反应速率i采用Butler-Volmer方程计算：

(4)

式(4)中：J0为交换电流密度；a为活性比表面积；β为电荷传递系数；F为法拉第常数；R为气体常数；T为电池运行温度；η为过电势。

1.1.2 气体传输

假设气体为理想气体且不能穿过质子交换膜，忽略压力差造成的对流传递，则膜两侧的气体传输过程可由菲克定律进行描述，如式(5)：

Si=·(-DiCi)

(5)

式(5)中：Di为气体在气体扩散层和催化剂层中的有效扩散系数；Ci为气体摩尔浓度；下标i表示气体种类，包括氢气、氧气和水蒸气。催化剂层内氢气的源项SH2和氧气的源项SO2使用式(6)计算：

(6)

水蒸气的源项SH2O需考虑膜结合水与水蒸气之间的相变Sad以及水蒸气与液态水之间的相变Sec：

(7)

(8)

(9)

式(7)～(9)中：ka为吸附率；kd为脱附率；Lcl为催化剂层厚度；Vm为质子交换膜等效摩尔体积；λ和λeq分别为膜含水量和膜中平衡水含量；γe和γc分别为蒸发率和冷凝率；Csat为饱和蒸气浓度。

1.1.3 水传输

液态水在阴极催化剂层和气体扩散层中的传输使用达西定律进行描述，方程如式(10)：

(10)

式(10)中：κ为液态水渗透率；μ为液态水黏度；Vw为液态水摩尔体积；pc为毛细压力；s为液态水饱和度；Ss为液态水源项，计算方法同Sec。

膜结合水传输过程可使用式(11)描述：

(11)

式(11)中：ξ为电迁移系数；Dλ为膜结合水扩散系数。

膜结合水源项Sλ的计算方法见式(12)：

(12)

1.2 模型参数及边界条件

模型中使用的主要参数值见表1。

表1 模型使用的主要参数值

模型的外部边界为流道与气体扩散层的交界面。假定阳极通入气体为纯氢气，阴极通入气体为空气，则边界处的气体摩尔分数可由式(13)～(16)计算：

(13)

(14)

(15)

(16)

2 结果与讨论

2.1 模型验证

为验证模型的可靠性，参照实验测试条件，配置模型运行参数，进行仿真，运行温度为348.15 K，阴、阳极进气相对压力分别为1.1×105Pa、1.3×105Pa，进气相对湿度为0.5。将模型仿真得到的极化曲线与实验数据进行对比，结果见图2。

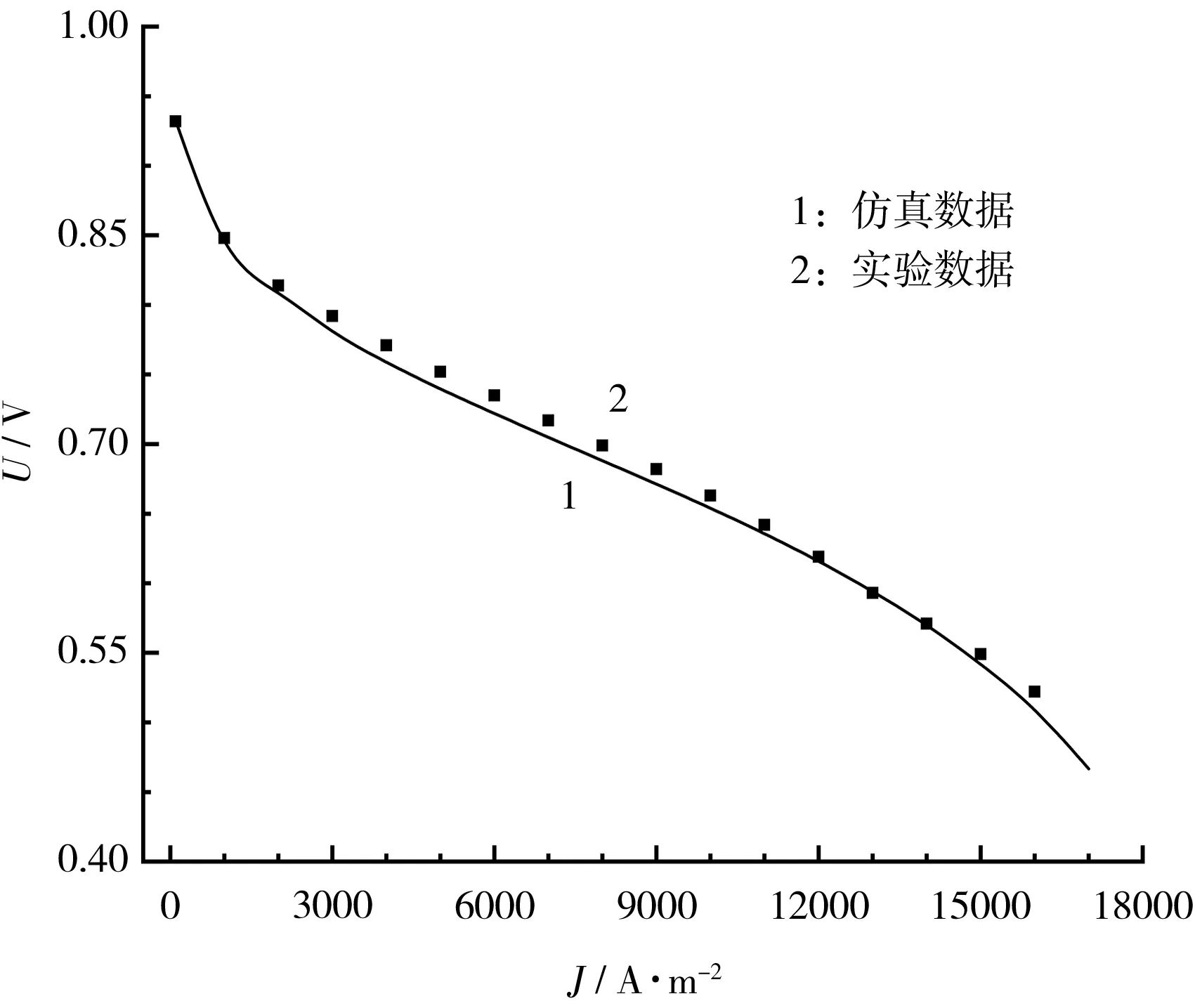
图2 模型极化曲线与实验数据对比

从图2可知，在电流密度从0 A/m2提高到17 000 A/m2的整个区间，模型仿真极化曲线均能很好地吻合实验数据，因此认为模型是可靠的。

2.2 燃料电池的动态响应

通过模型仿真对燃料电池的动态响应进行研究。先将电流密度保持在3 000 A/m2，运行至第5 s时，阶跃升高至6 000 A/m2，以此来模拟实际应用中的负载突变工况。在电池运行温度为348.15 K，阴、阳极进气相对压力分别为1.1×105Pa、1.3×105Pa，进气相对湿度为0.4的条件下，电流密度阶跃变化时电压和膜含水量的动态响应见图3。

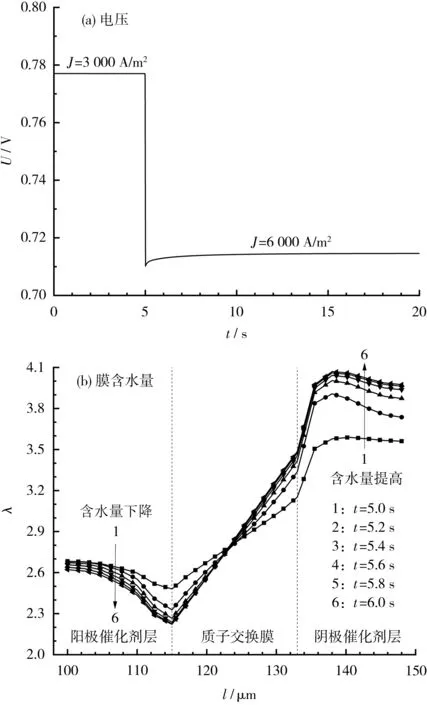
图3 电流密度阶跃变化时电压和膜含水量的动态响应

仿真建立的小尺寸模型，反应气体浓度的过渡时间可忽略不计，因此输出电压从瞬态变为稳态的变化趋势，主要受膜含水量的影响。从图3(a)可知，电流密度阶跃升高，导致电压从0.777 V瞬间降至最低值0.710 V，原因是活化过电势和欧姆过电势同时升高；随着反应的进行，膜含水量不断增加，使膜电导率提高，欧姆过电势下降，因此输出电压会在骤降后缓慢提升，在0.715 V左右达到稳态。该现象被称作电压下冲。从图3(b)可知，当电流密度从3 000 A/m2突变至6 000 A/m2时，膜含水量的平衡状态被打破，阳极侧受电迁移的作用，含水量在短时间内有所下降，而阴极侧在电迁移和反应生成水的双重作用下，含水量有所提高。随着反应的进行，上述变化规律仍存在，但速度会因反扩散作用而减缓，当电迁移速率与反扩散速率平衡时，膜含水量恢复稳态。

2.3 进气条件对动态响应特性的影响

2.3.1 进气相对湿度

在电池运行温度为348.15 K，阴、阳极进气相对压力分别为1.1×105Pa、1.3×105Pa的条件下，改变进气相对湿度。不同湿度条件下燃料电池膜含水量积分和输出电压的动态响应曲线见图4。

图4(a)中膜含水量沿垂直膜方向的积分，可以表示膜内的总含水量。从图4(a)可知，进气相对湿度越高，膜内总

图4 不同进气相对湿度时膜含水量积分和电压的动态响应

含水量越多。膜内总含水量增多会导致膜电导率升高，进而降低欧姆过电势。当进气相对湿度为0.4和0.6时，膜内总含水量在电流密度突变后逐渐提高至稳态值；当进气相对湿度为0.8和1.0时，膜内总含水量在电流密度突变后先提高到峰值，再缓慢降低至稳态值。膜含水量会影响欧姆过电势，因此在图4(b)中，进气相对湿度越高，电流密度阶跃变化前后的稳态电压值越高，下冲幅度也越小。电压在不稳定区间内的响应曲线可与图4(a)中膜含水量的变化过程对应。

2.3.2 进气压力

进气压力直接影响燃料电池入口处的反应物浓度。在电池运行温度为348.15 K、进气相对湿度为0.4的条件下，取多组进气压力值进行仿真，得到燃料电池输出电压的动态响应曲线，如图5所示。

从图5可知，在不同进气压力条件下，燃料电池的输出电压在电流密度阶跃变化过程中均出现下冲现象，且下冲幅度基本相同，说明进气压力对输出电压在不稳定区间内变化趋势的影响不大。由模型边界条件可知，在进气相对湿度和入口气体温度相同时，通入燃料电池阴极侧的氧气浓度会随着进气压力的增大而升高，氧气浓度升高会使得阴极的交换电流密度增大，进而降低活化过电势，因此在图5中，进气压力越大，电流密度阶跃变化前后的稳态电压越高。