三峡出闸船舶航速分布规律与预测应用
2021-05-29何进朝周昔东母德伟程志友黄荣超
何进朝, 周昔东, 母德伟, 程志友*,黄荣超
(1.重庆交通大学西南水运工程科学研究所,重庆 400016;2.重庆交通大学航运与船舶工程学院,重庆 400074;3. 长江海事局后勤管理中心重庆分中心,重庆 400011)
长江三峡船闸是制约长江中上游航运的关键通航枢纽,船舶出闸效率影响着三峡船闸的运行效率。为了揭示出闸船舶安全航速的变化规律、监控出闸船舶异常航速、科学调度出闸船舶、提高船舶出闸效率和保障船舶出闸安全,研究三峡出闸船舶航速分布规律与预测应用问题。
船闸引航道和口门区通常会产生非恒定的往复流,形成存在斜流、回流、涌浪等不利船舶航行的复杂水流流态[1]。复杂的水流条件对船舶出闸航行有很大的影响,航速过高,船舶航行安全不能保证;航速过低,船舶航向难以控制,并增加了船舶出闸时间,致使船闸通过能力降低,因此,根据船闸引航道通航水流条件及交通环境选择合适的安全航速是操船者应予以考虑的问题。为了定量地揭示内河船舶在航道中应采取安全航速的规律,文献[2]以船舶航行的船舶自动识别系统(automatic identification system,AIS)信息为数据来源,利用直方图法分析了船舶在航道内的速度分布规律,并利用折线图法分析了船舶船长对船舶速度的影响规律。为了让船舶安全、快速地到达目的地,文献[3]通过结合船舶行驶的特点和影响因素建立了针对于船舶航行的航线诱导模型。文献[4]建立基于交替稀疏自编码(altericating sparse auto-encoders,ASAE)深度学习模型,预测了海洋气象对船舶航速的影响。为了改进海上船舶监控系统的效果,有效地预测船舶在海上航行行为,文献[5]建立了基于极限学习机的船舶行为预测模型,从而提高了对船舶行为的预测精度。为了降低船舶在港口以及航道中碰撞风险,文献[6]对建立了船舶穿越间隙的模型,通过模型的计算得到,船舶在选择合适的时机和适当的航速进行穿越,可以降低船舶碰撞风险。文献[7]和文献[8]分别基于卡尔曼滤波和灰色预测方法建立船舶航迹预测模型,通过建立船舶运动状态方程实现了对船舶运动状态的预测。文献[9]基于AIS数据运用BP(back propagation)神经网络对船舶航行行为进行了预测;Simsir等[10]、Zissis等[11]利用人工神经网络对船舶航迹进行了实时预测。
以往相关研究主要集中在对船舶航行行为和航迹预测领域,而对于船舶出闸航速分布规律及预测应用的研究还较少涉及。因此基于AIS统计数据分析三峡出闸船舶航速分布规律,建立基于BP神经网络的三峡出闸船舶航速预测模型,为科学调度出闸船舶、提高船舶出闸效率和保障船舶出闸安全提供技术支撑。
1 三峡出闸船舶航速分布规律
模型构建流程如图1所示。

图1 模型构建流程Fig.1 Construction process of model
1.1 影响三峡出闸船舶航速的主要因素分析
三峡船闸下引航道全长2 708 m,口门区长 530 m[12],三峡船闸下引航道和口门区的长度为 3 238 m。如图2所示。

图2 三峡船闸下引航道、口门区平面布置图Fig.2 Layout plan of approach channel and entrance area of Three Gorges ship lock
1.1.1 通航水流条件对船舶出闸速度的影响
三峡船闸引航道和口门区存在斜流、回流、涌浪等不利船舶航行的复杂水流流态,船舶在引航道中的位置不同,所遭遇的水流条件也不同,因此所采取的安全航速也不同。
长江干线通航标准规定,引航道口门区的表面最大流速应满足平行于航线的纵向流速不超过 2 m/s、垂直于航线的横向流速不超过0.3 m/s、回流表面流速不超过0.4 m/s,可见通航水流条件对船舶出闸航速有显著影响。
1.1.2 船舶尺度对船舶出闸速度的影响
根据船舶操纵知识可知,船舶长度L和宽度B的比值与船舶的快速性和操纵性有关。
船舶长度与宽度的比值越大,表示船舶越狭长,快速性好,航向稳定性好,但港内操纵不灵活,因此船舶尺度对船舶出闸速度有一定影响。
1.2 三峡出闸船舶航速分布规律
1.2.1 统计数据来源与处理方法
1)统计数据
课题组收集了2018年1月、5月、7月三峡出闸船舶的AIS数据。由于货船占统计船舶总数的85.72%,所以本文主要研究货船的航速分布规律。根据对船舶出闸航速研究的需要,在对收集的AIS数据进行筛选,并重点筛选以下数据:船舶名称、水上移动通信业务标识码(maritime mobile service identify,MMSI)、船长、船宽、经度、纬度、船舶航速。
2)船舶出闸速度统计方法
船舶在引航道和口门区内的速度分布统计分析步骤如下:
通过对纬度的限制筛选可以得到船舶出闸的经纬度以及每一经纬度所对应的航速。利用中分纬度计算方法,计算各点的距离,以及各点到船闸的距离,即
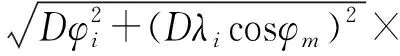
(1)
(2)
式中:di→i+1为第i个点到第i+1个点的距离,为船位航迹点间距;D为第i+1个点到船闸的距离;φ为航迹点的纬度;λ为航迹点的经度。由于所研究的航段处于中纬度地区,且这段航段距离不长,所以可以用两点的平均纬度代替中分纬度计算[13],即φm≈0.5(φi+1+φi)。
通过式(1)和式(2)以及对应的AIS数据,可以得到不同船舶到船闸的距离和航迹点之间的间距以及对应航速。
1.2.2 船舶离闸距离与航速的关系
船舶在出闸引航道中的位置不同,所遭遇的通航水流条件不同,因此船舶的航速也不同。由于出闸航道约3 300 m,根据航道特征将出闸航道分为三段(以船闸起算):0~900、900~1 800、1 800~3 400 m。基于船舶离闸距离与出闸航速的关系,统计分析如下:
(1)在距离船闸0~900 m,船舶航速约85%分布在4~11 kn(1 kn=1海里/h),约50%分布在 6~9 kn。如图3(a)所示。
(2)在距离船闸900~1 800 m内,船舶航速约70%分布在7~11 kn,约40%分布在9~11 kn。如图3(b)所示。
(3)在距离船闸1 800 ~3 400 m内,船舶航速约80%分布在8~13 kn,约50%分布在10~13 kn之间,如图3(c)所示。

图3 不同船闸距离的航速分布直方图Fig.3 Histogram of speed distribution of different distances of ship and lock
由图3可以得出,船舶在出下引航道时,航速是随着离船闸距离增大而逐渐增大,船舶在距离船闸1 800 ~3 400 m内航速逐步趋于稳定。
1.2.2 船舶尺度与航速的关系
船舶长度与宽度的比值与船舶的快速性和操纵性有关;因此船舶尺度不同,船舶在出闸引航道中的航速也不同。参考《长江干线通航标准》船舶吨位分类,将出闸船舶依据船长分为三类:船长 90 m及以下船舶(1 000 t级及以下)、船长 的船舶(2 000 t级)、船长100 m及以上的船舶(3 000 t级及以上)。
(1)船长90 m及以下的船舶出闸航速分布在10~14 kn的频率为72%。如图4(a)所示。
(2)船长90~99 m的船舶出闸航速分布在8~13 kn的频率为73.5%。如图4(b)所示。
(3)船长100 m及以上的船舶出闸航速分布在6~12 kn的频率为76.1%。如图4(c)所示。
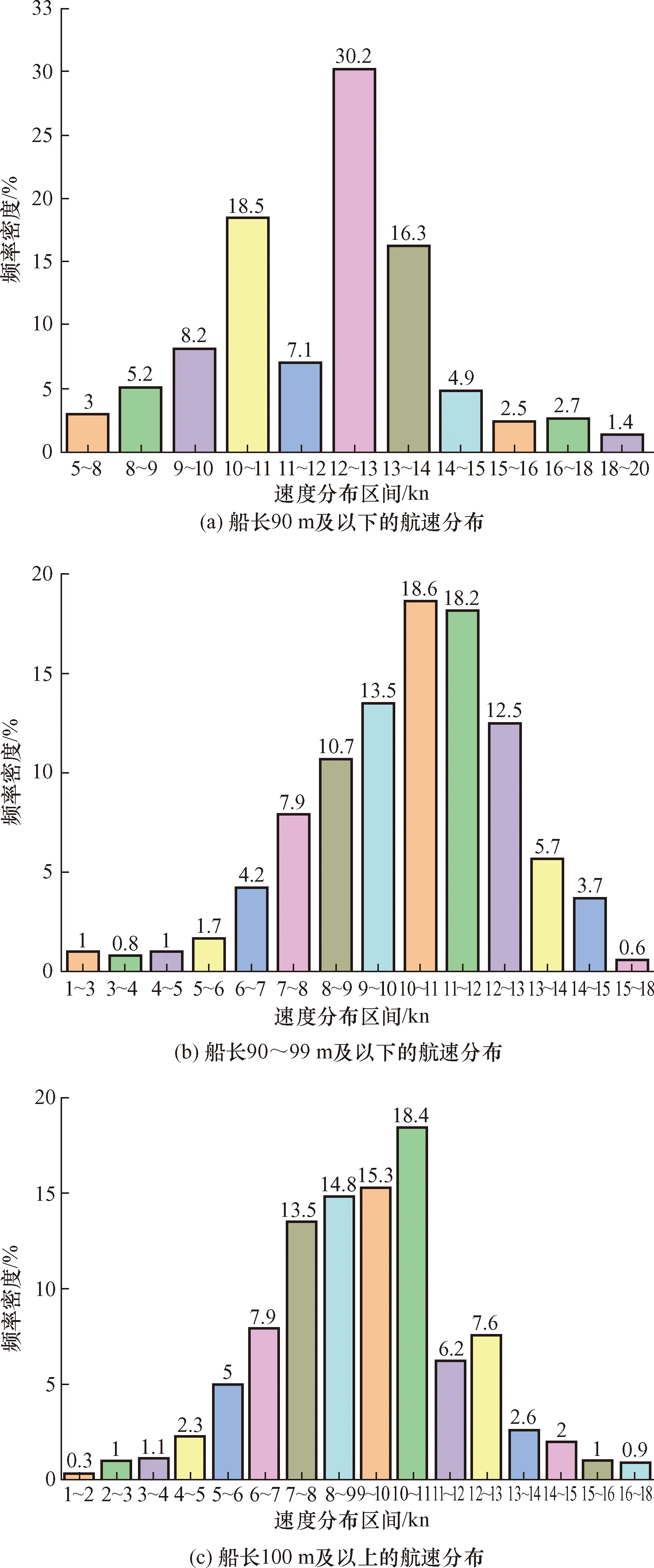
图4 不同船长的航速分布直方图Fig.4 Speed distribution histogram of different captains
通过对比图4可以得出船舶在出下引航道时,船长越小其出闸航速相对越大。
2 基于BP神经网络的三峡出闸船舶航速预测模型
2.1 BP神经网络的基本原理
BP神经网络是一种基于误差反向传播的算法,其结构主要分为输入层、隐含层和输出层,各层神经元相互连接,同层神经元之间不连接[14]。BP神经网络模型的学习过程中,主要分为信号正向传播和误差的反向传播两部分。
2.1.1 信号正向传播算法
当信号正向传播时,数据信号从输入层输入,经隐含层传向输出层传递,若输出的实际值与理想值差异较大,则误差进行反向传播修正。设n为输入节点,m为隐含层节点数,k为输出层节点;则有以下关系。
1)第i个神经元结构的输入
(3)
式(3)中:wij为输入层第i个神经元与输出层第j个神经元的连接权值;Oj为输出层第j个神经节点的输出值。
2)第i个神经元结构的输出
Oi=fRelu(hi),i=1,2,…,k,
(4)
式(4)中:fRelu为节点i和j之间进行传递激活的 Relu函数。
2.1.2 误差逆向传播算法
在模型的运算过程中,如果输出值与实际值相差太大时,就需要将误差信号经隐含层反向传递给输入层,此时选取误差目标函数为
(5)
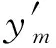
修正误差权值计算公式为
(6)
式(6)中:α为恒正学习速率。
在误差逆向传递时,利用式(6)不断的修正加权系数,将误差传递给各层的神经元结构,实现神经元之间的连接值的实时调整,直至输出层得到理想的输出结果为止[15]。
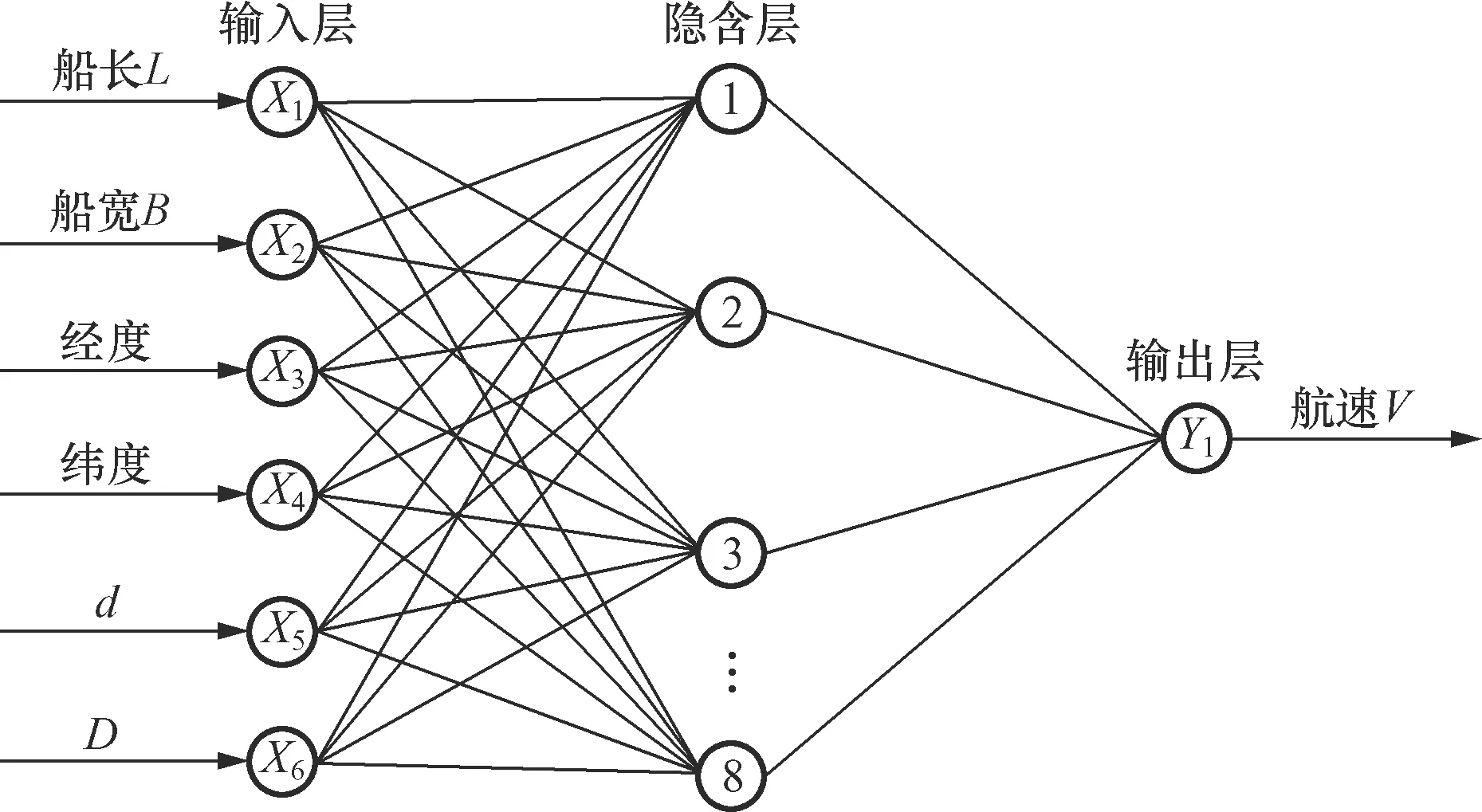
图5 基于BP神经网络的三峡出闸船舶航速预测模型Fig.5 Prediction model of ship speed for the Three Gorges Dam based on BP neural network
2.2 基于BP神经网络的三峡出闸船舶航速预测模型
2.2.1 模型的输入和输出层
根据前文船舶尺度、离闸距离对船舶出闸航速的影响,同时考虑增加输入因素以提高模型预测的精度,选择船舶长度L、船舶宽度B、船位经度、船位纬度、船舶到船闸的距离D、船舶两航迹点的间距d作为模型的输入层。隐含层节点数为8,通过计算机试验得出。船舶出闸航速V作为模型的输出层。
2.2.2 基于BP神经网络的三峡出闸船舶航速预测模型
综上所述,得到基于BP神经网络的三峡出闸船舶航速预测模型,如图5所示。
2.2.3 模型的训练
1)选取样本数据
选择所获取的AIS数据样本(船长L、船宽B、经度、纬度、航速)中的80%,在此基础上通过样本的经度、纬度数据解算出船舶离船闸的距离D、船舶两航迹点的间距d,得到模型训练的6个输入数据(船舶长度L、船舶宽度B、船位经度、船位纬度、船舶离船闸的距离D、船舶两航迹点的间距d)和模型输出航速V。
2)数据归一化处理
本文所选取的输入层的数据量纲差异性很大,为了使得到的预测结果更加的精准,现将输入数据、输出数据统一变成[0,1]区间内的量纲值,以减小不同数据间的量纲差异,提升学习效率和精度。进行归一化处理[12]:
(7)
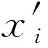
3)模型的学习训练
为了提高模型的学习训练效率,加快模型的收敛速度,模型选取RmsProp为训练函数,激活函数为Relu,学习率为0.005。当训练次数为50次左右时,模型可以达到目标误差的范围以内,即精度符合该模型的要求。
2.3 模型检验
2.3.1 模型的预测误差分析
所建立的BP神经网络模型经过学习训练后,可以得到训练集和验证集的预测值,将预测值与实际值进行相对误差计算,得到相对误差。计算公式为
(8)
由于将80%的AIS数据用于模型的训练,故将20%的AIS数据用于模型的检验。船舶预测的速度值与实际速度值变化趋势基本一致,如图6所示。利用式(8)计算相对误差的平均值,得到平均相对误差为6.7%。
2.3.2 模型检验
在检验航速预测的效果时,采用单因素方差来分析[16]船舶出三峡船闸下引航道和口门区速度的航速预测效果,即计算航速预测值与航速实际值有无显著性差异。在给定显著水平α=0.05的情况下,单因素方差来分析如表1所示。
从表1可以得出:F=0.503

图6 20%的AIS数据的速度对比关系图Fig.6 20% AIS data velocity comparison diagram

表1 20%的AIS数据的单因素方差来分析Table 1 20% of AIS data were analyzed by one-way ANOVA
通过单因素方差来分析得到的结果和图6结合可知,采用BP神经网络航速预测模型得到船舶在出闸航道的航速与实际航速较为接近,可以用此模型对出三峡船闸下引航道和口门区的船舶航速进行预测。
3 模型应用
2019年5月某一闸次,某船长108 m、船宽 18 m的船舶出闸,利用图5的模型对其出闸航速进行预测,其在不同位置的预测航速如图7所示。
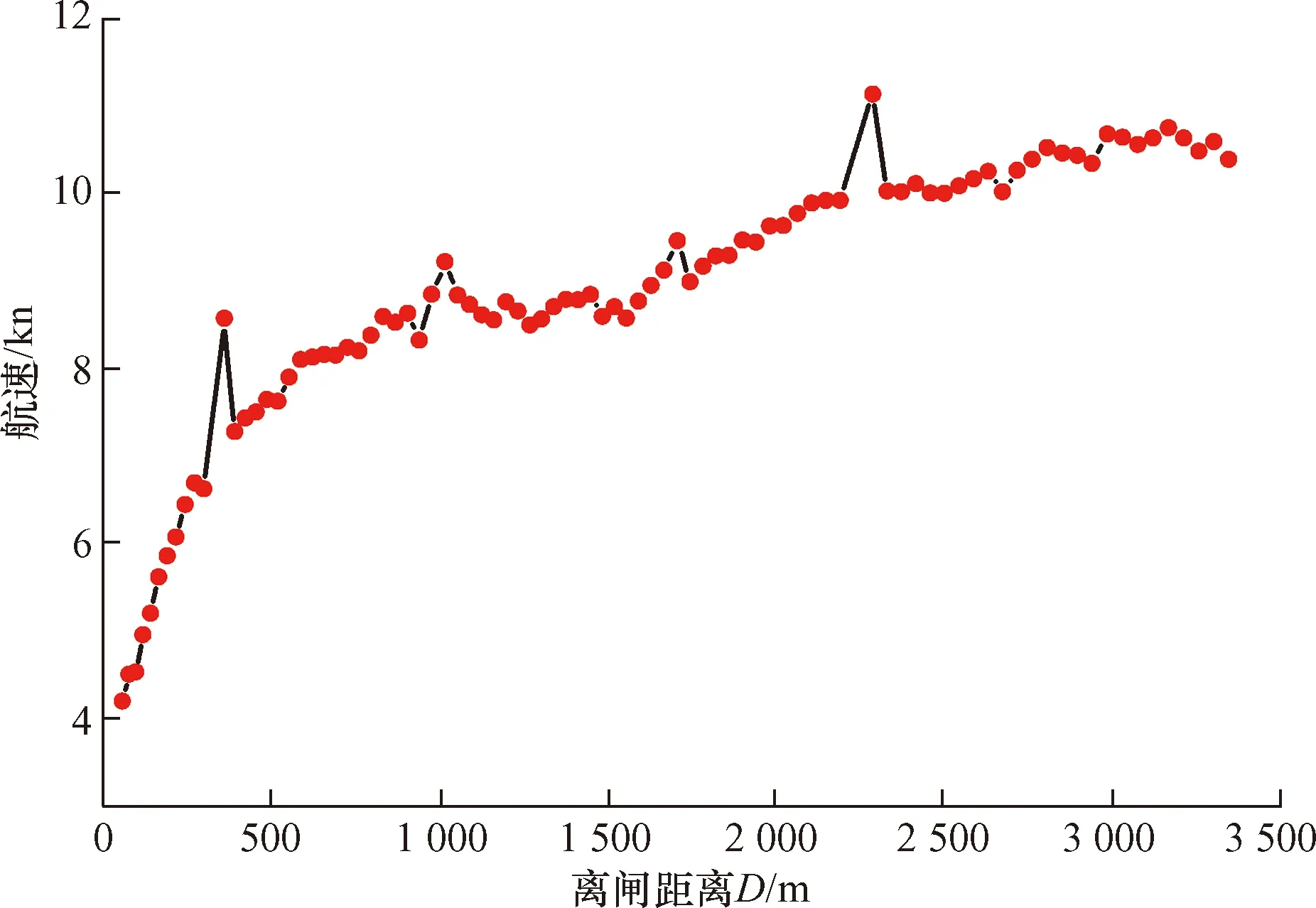
图7 L=108 m的船舶出闸航速预测Fig.7 Prediction chart of ship speed at L=108 m
由航速预测图形可知:船舶离闸距离1 000 m以内航速增加较快,航速从4 kn增加到9 kn左右;船舶离闸距离1 000~2 500 m以内航速保持较慢增加,航速从9 kn左右增加到10.5 kn左右;船舶离闸距2 500~3 500 m以内出闸航航速稳定在10.5 kn左右。由此,根据引航道通航条件和出闸航速变化规律,该船离闸距离1 000 m以内应注意保持与前后船之间的间距,并加强与前后船舶之间的通信联系;该船离闸距离1 000~2 500 m,应结合通航水流条件对船舶航行的影响合理使用主机以适应航速的变化规律;该船离闸距离2 500~3 500 m,船舶应注意通航环境变化将以稳定的航速出引航道。
4 结论
船舶在出三峡船闸下引航道时,航速是随着离船闸距离增大而逐渐增大,船舶在距离船闸1 800~3 400 m内航速逐步趋于稳定;船舶在出下引航道时,船长越小其出闸航速相对越大。本文建立的以船长、船宽、纬度、经度、船舶离船闸的距离、船舶航迹点的间距为输入层的航速预测模型,其航速预测值与实际航速之间平均误差为6.7%,采用单因素方差分析了模型的预测航速和实际航速,得到预测值与实际值并无显著性差异。研究得到的三峡出闸船舶航速预测模型可以用于科学调度出闸船舶、监控出闸船舶异常航速状态。
