指向深度学习的数学讲评课微思考

卞冬梅

【摘要】数学教学中，试卷讲评课的教学发挥着至关重要的作用。与新授课一样，教师要时刻关注学生的发展，走出“满堂灌”的误区，带领学生走向深度学习，解放学生的脑、手、嘴等，从而培养学生的数学学习能力。

【关键词】小学数学;讲评课;试卷讲评

在数学教学中，试卷讲评课的教学发挥着至关重要的作用。随着新课程改革的深入，数学教学发生了一系列变化。但当前阶段，试卷讲评课教学仍存在一定的不足。例如，一些教师只是简单讲解一些题目，形式比较单调，收效甚微。教师们往往会抱怨，题目讲了一遍又一遍，可不懂的学生还是不懂。在复习阶段，讲评课的重要性更是不言而喻。讲评课的师生状态呈现出以下镜头。

镜头一：讲评课该讲什么、如何讲，许多教师模糊不清，教学十分随意，重难点不突出。一些教师会详细讲解每道题，缺乏层次性和针对性。这样的讲评课看似对每个知识点面面俱到，一堂课下来，教师讲得非常疲惫，学生听得昏昏欲睡，遇到了涉及思維挑战的题目时，师生都已筋疲力尽。

镜头二：学生正襟危坐，教师只顾自己讲得津津有味，并未给学生预留思考的空间和时间。一堂课下来，能参与回答问题的学生很少，即使有学生发言，也多停留在说出答案的层面，较少调动思维。

基于以上情况，笔者认为，教师应提高数学讲评课的效率，转变传统的试卷讲评课的模式。

一、精准梳理，以知识点带题

“圆柱和圆锥”这一单元的知识点不多，但涉及圆柱的表面展开图、表面积（侧面积）和体积、圆锥的体积，试卷中单纯运用公式解决问题的题目不多，题目变化较大，部分题目有深度和难度。在评讲试卷前，笔者先带领学生回顾本单元的知识，进行简单的梳理，然后由知识点引出相关的习题。

例如，在回顾圆柱表面积的计算方法后，笔者带领学生到试卷上寻找考查圆柱表面积知识的题目。很快，学生便找出了试卷上所有和求圆柱表面积的知识有关的题目。把他们归到一类后，笔者引导学生进行分析：有些题目可以用公式直接求出，而有些题目已经发生变化，但不管怎么变，仍可以在正确理解表面积概念的基础上解决。在找题的过程中，不时有学生懊恼自己“中了计”（没注意到单位名称的不统一、忽视了现实情况中只有一个底面的情况等）。当多名学生对同一道题存在理解困难或有疑惑时，笔者再重点讲评，此时学生的听课欲望要高涨许多。如此让学生经历“知识梳理—题型归类—发现问题—解决问题”的过程，能取得更理想的教学效果。

二、科学诊断，从错题中寻因

在讲评中，教师应先统计并分析学生的答题情况，从而做到有的放矢。对于一般练习，教师批阅时可在错误率比较高的题目旁做上记号;对于调研卷，教师应分析试卷考查知识点的分布密度和深度情况，结合学生的答题情况，既要总体把握班级学生的整体学习水平，又要逐题分析学生在各题的失分原因，从而确定讲评的重点和难点。

例1：将圆柱的底面半径扩大5倍，高不变，那么它的侧面积（    ）。

A.扩大5倍      B.扩大10倍      C.扩大25倍

这是一道教师认为错误率不高的基础题，但统计结果显示这道题的失分率高达32.6%。面对如此高的失分率，教师询问出错的学生才知道，他们受到圆形中半径变化带来的面积变化影响，看到“半径扩大5倍”马上就得出“侧面积扩大5的平方倍”的结论。

例2：有一个棱长为4分米的正方体蜡块。如果将它熔铸成一个圆柱，那么圆柱的体积是（    ）立方分米;如果将它削成一个最大的圆锥，那么这个圆锥的体积是（    ）立方分米。

这道题的错误率很高，第一空的错误率为37.6%，第二空的错误率为52.8%。究其原因，部分学生对“熔铸”一词理解有误，将其和“削成”的概念相混淆。因此，在教学时，教师应帮助学生厘清“熔铸、削成”的概念。在回答第二个问题时，一些学生直接用第一问的结果乘以1/3，还有一些学生求出削成的圆柱的体积后忘记了乘以1/3。

例3：一个底面半径为r厘米的圆柱形容器内盛有适量的水，将一个圆锥形铁锤浸没在水中，水面上升了h厘米，那么这个圆锥形铁锤的体积是（     ）立方厘米。

A.πr²h       B.1/3πrh      C.1/3πr²h

错误集中在C选项上，选择C的学生看到圆锥的体积不加思索就会想到用圆柱的体积乘以，却没有考虑此题看似是求圆锥形铁块的体积，但实质已转化成圆柱形容器中上升的水的体积。此题似乎与例1的错因无关联，但本质都在于没有真正理解“圆锥的体积要用底面积×高×1/3”的内涵。

三、有效配合，借评题促发展

有效的讲评课是发展学生思维、提升教学质量的重要手段，但高效的讲评课并不是就题讲题，而应以题目为依托，促进学生各方面的发展。

（一）解放学生的脑，在敏思中发挥潜能

传统的课堂教学中，在学生遇到困难时，教师通常会在最短的时间内给予学生指导，导致学生对教师的依赖性较强。在试卷讲评课上，教师应为学生预留充足的思考时间。例1错误率高足以说明学生未能养成积极思考的习惯，如果讲评课上教师仍以主讲人的角色不断向学生灌输知识，将不利于对学生思维能力的培养。因此，教师不能一味地“谆谆教导”，而要减轻学生机械记忆的负担，使学生养成积极思考的习惯，从而发掘学生潜能，提高其数学思维能力。

（二）解放学生的手，在操作中强化认知

针对例2出现的问题，若教师仅训斥学生或强调一句“怎么又忘记乘以1/3了呢？一定要记住，求圆锥的体积一定要用底面积×高×1/3”，学生是不会产生深刻印象的，这样的教学是无力的。教师不妨换一个角度，追问学生：为什么求这个圆锥的体积要乘以呢？这样一来，学生便能回忆概念学习时的操作。教师可以请出错的学生借助学具盒里的学具再演示一遍加深理解，同时也可以联系求长方体、正方体体积的公式，让学生感受所有直柱体的体积都可以用底面积×高直接求得，而圆锥不是直柱体。

陶行知先生说：“‘做是在‘劳力上劳心的‘做，行是知之始，知是行之成。”[1]这一教育思想针对传统教学中重知识、轻能力的做法，提出了“教学做合一”的新理论;针对传统教学造成的学生“体脑分离”的弊端，提出了需要手脑并用的新目标，强调了操作在教学过程中的积极意义和重要作用。以往在新课教学中，教师仅带领学生实践一次，便认为学生能够灵活运用所学知识了。但对于一些注意力集中情况不理想的学生及接受能力较弱的学生而言，仅进行一次实践是远远不够的。这要求教师多带领学生进行实践，使学生在操作过程中感受知识的发生和形成过程。

（三）解放学生的嘴，在争辩中加深理解

在教学过程中，教师应鼓励学生敢于、善于表述自己的想法和观点，可以和同学讨论，也可以和教师讨论，这一环节能很好地帮助教师根据学生的正确理解或错误理解来调整教学进度。针对例3出现的问题，一些学生始终没有理解：题目明明是求圆锥形铁锤的体积，为什么不用乘以呢？此时，教师可以先让学生展开讨论，让学生发现问题的本质，使其了解转化的过程。实践证明，许多思维的飞跃和问题的解决正是在争辩的过程中实现的。因此，在讲评课上，教师应基于一些学生的正确想法，为其搭建互相争辩的平台，让学生在互相争辩的环境中认真思考，从而加深对知识的掌握，推动数学思维的发展。

（四）解放学生的眼，在生活中寻找数学

數学源于生活，在讲评课上，教师不能就题讲题，要让身边的数学知识走进课堂，同样也要引导学生把所学数学知识应用到现实生活中。

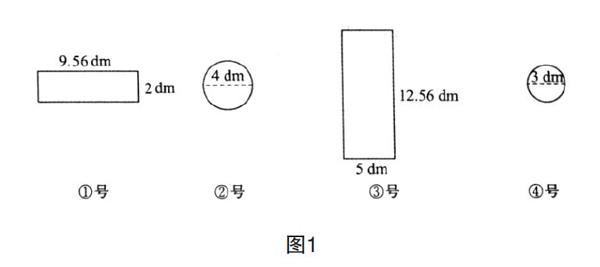
试卷上有这样一道题：请你制作一个无盖的圆柱形水桶，有以下几种型号的铁皮可供搭配选择（见图1）。

（1）你选择的材料是（   ）号和（   ）号。

（2）你选择的材料做成的水桶最多能装水多少千克？（按1升水的质量是1千克计算）

这道题的错误率不高，如果教师在课堂上仍一味地讲解该题目，学生的学习兴趣自然不高。此时，教师应改变题目信息，创设生活情境。比如，王大爷要做一个油桶，可是他只有一张长方形铁皮，长15.7分米，宽6.28分米，你能帮他去商店再配两个底吗？这个问题与生活贴近，虽然从理论上说有两种配底面的方法，但从实际考虑，只有把15.7分米作为底面周长时制作出来的油桶才更美观。

讲评有法，但无定法，教师只有开展深度教学，才能实现学生的深度学习。教师只有坚持每节讲评课都进行深度钻研，才能提高讲评课的效率，让讲评课变得有温度、有深度、有厚度、有广度，从而达到事半功倍的效果。

【参考文献】

陶行知.陶行知教育箴言[M].福州：福建教育出版社，2014.