基于自适应GA-SA算法串联机械臂轨迹运行时间优化
2021-05-28魏裔军
周 晟,魏裔军
(武警士官学校基层后勤管理系被装教研室,杭州 310000)
0 引言
现代化工业生产中,机械臂的适用范围、使用频率、工作需求越来越大。串联机械臂是其中的基础类型,在生产生活中扮演着重要的角色。因此,优化工作轨迹、缩短生产时间、提高工作效率,具有十分重要的意义,亦是现代机械臂研究的重要方向。
文献[1]在运动学约束下,以遗传算法(GA)为工具,针对轨迹运行时间和平稳性性能实现优化设计。文献[2]针对送料机械手进给、下降、松开、回退、夹紧、提升等基本作业运行时间,选取遗传算法结合B样条曲线,对时间最优化模型实行轨迹规划和优化设计。文献[3]在传统遗传算法基础上引入模拟退火算法(SA),有效跳出局部最优,降低求解时间,提升运算效率。
针对机械臂轨迹规划时间最优模型,GA在优化设计中能够弥补SA在寻优时的不足,因此,文中提出一种自适应GA-SA算法[4-5]。选取PUMA762串联机械臂运行轨迹为优化对象,利用3-5-3次多项式进行运行轨迹插值计算后,以最优运行时间为目标构建目标函数,合理设置约束条件下通过自适应GA-SA算法实现时间最优化设计。结合ADAMS绘制虚拟样机模型,合理设定相关参数进行仿真分析,验证算法的有效性,为后续研究提供理论支撑。
1 模型构建与工作空间求解
1.1 模型构建
文中设置PUMA762串联机械臂为主体对象进行仿真模拟,以运动学理论为基础绘制D-H参数,如表1所示[6]。

表1 D-H参数表
表1中:αi表示连杆扭曲;ai表示连杆长度;di表示连杆偏置;θi表示关节转角。
以表1为基础构造机械臂连杆模型,设置关节坐标系,如图1所示。
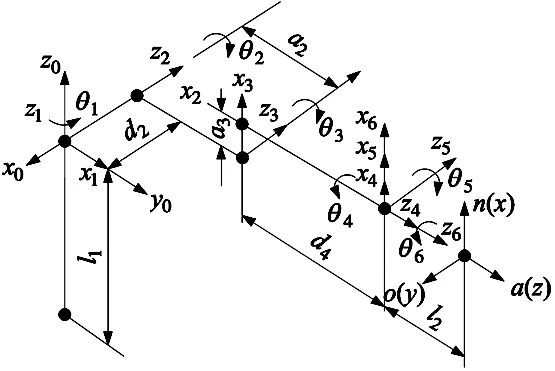
图1 关节坐标系
运用MATLAB工具箱构建机械臂结构模型图,如图2所示。
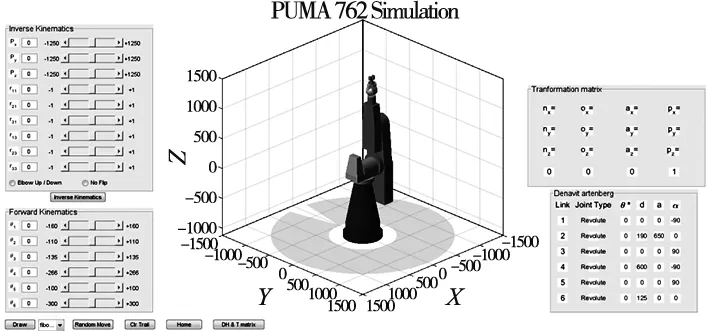
图2 机械臂结构模型图
1.2 工作空间求解
依据图2机械臂结构模型图,验证正、逆解求解的正确性,并借助机械臂正解模型,采用蒙特卡洛法求解工作空间,求解步骤如下所示[7-8]:
步骤1:通过运动学正解模型,计算末端执行器MARK点在坐标系中的位置向量;
步骤2:末端执行器空间位置集合Wn如下所示:
(1)
式中,f(x)为机械臂正运动求解;λ(x)为机械臂末端点空间位置。
步骤3:依据蒙特卡洛法,将rand函数随机生成数值设置为随机变量步长,关节变量等式如下:
(2)
步骤4:将步骤(3)所求N个关节变量的伪随机值代入运动学方程中,求解末端执行器MARK点位置向量函数值,以点阵方式反映实际工作空间。
根据上述步骤,绘制PUMA762机械臂末端执行期无碰撞下,所能达到所有点的集合,以图像显示的方式构建机械臂工作空间,如图3所示。
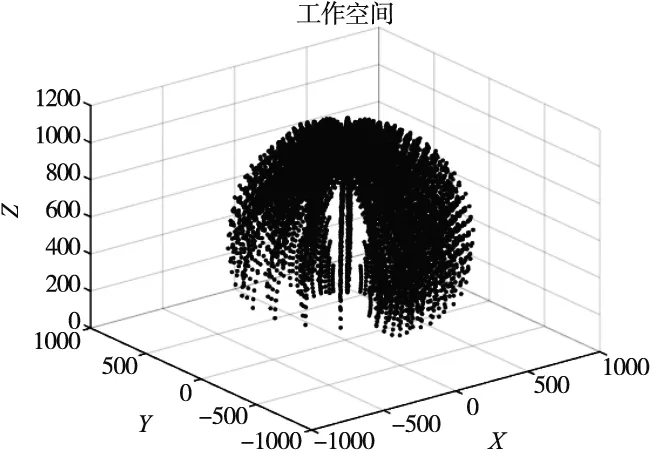
图3 PUMA762工作空间
2 目标函数构造与轨迹规划
2.1 目标函数构造
机械臂末端执行器在满足运动学约束、动力学约束和负载约束件下,以工作时间最优化目标,其目标函数与约束条件束设计如下:
(3)
式中,tij为第i个关节运行轨迹的第1、2、3段的运行时间;h(t)为第i个关节完成运行轨迹总时间;j=1,2,3。
(1)运动学约束
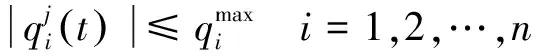
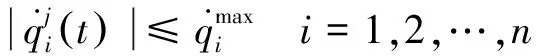
(2)动力学约束
假定机械臂未发生碰撞,则τf=0
负载约束:Fgmin≤Fk≤Fgmaxk=1,2
式中,Fk为末端执行器夹持力;Fgmin为最小夹持力;Fgmax为最大夹持力;
2.2 3-5-3次多项式插值
作业过程中,已知起始点、路径点、终止点位于笛卡尔坐标系的空间坐标值,运用运动学逆解模型,分析求解各关节在4个插值点处的关节角度,θij表示关节i的插值角度,i=1,2,…,n,n表示关节个数,j=1,2,3,4,表示4个插值点的序号。
第i段关节3-5-3次多项式插值通式如下所示:
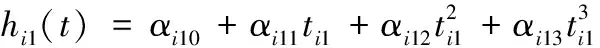
(4)
式中,hi1、hi2和hi3分别为第i个关节的第一、二、三段三次、五次、三次多项式运行轨迹;αi1j、αi2j和αi3j分别为多项式系数;ti1、ti2和ti3分别为第i个关节第一段、第二段和第三段运行轨迹的运行时间。合理运用14个边界和过渡约束条件,可求解出3-5-3次多项式中未知系数aij,推导公式如下所示。
等式(5)中A仅与第i个关节3段多项式的插值时间ti1、ti2和ti3有关,等式(7)表示第i个关节角的位置矩阵。
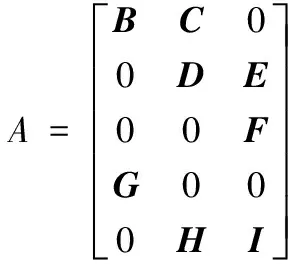
(5)
θ=[0 0 0 0 0 0θi30 0θi00 0θi2θi1]T
(6)
(7)
式中,

3 算法原理及步骤
3.1 传统算法的缺陷
(1)传统GA设置固定的pm值与pc值,无法兼顾优化前期,须对全局具有较强搜索能力,优化后期,保障新个体产生等多方面需求。
(2)传统SA求解时间较长,面多变量多、目标函数复杂情况时,若控制参数T初始值较大,迭代次数较多,若T初值较小,较难计算求解全局最优解。并且,由于SA局部寻优的限制,所获取的局部最优解质量可能并不很高。
3.2 自适应GA-SA算法
本文设计了GA与SA结合的自适应GA-SA算法[9-10]。
(1)交叉概率pm与变异概率pc在GA优化过程中所呈现的数值状态,对其优化性能、分析结果具有巨大影响。GA优化前期阶段,从全局层面考虑需要较强的全局搜索能力,降低局部优化的干扰,此时就需要较大的pm值与较小的pc值,以保证搜索初期对全局的掌握。进入优化后期,就需要较小的pm值与较大的pc值,以保证新个体的产生,固定的pm值与pc值就无法达到这样的要求。
因此,文中在GA设计时采用自适应方法,使得pm值与pc值按照等式(8)、等式(9)随适应度函数变化而改变,实现自适应变化。
(8)
pm=
(9)
式中,fmax,fmin,fave分别表示适应度函数最大值、最小值、平均值;δ表示适应度函数值宽度预计值;pc1、pc2分别表示设定交叉概率的最大值、最小值;pm1、pm2分别表示设定变异概率的最大值、最小值。
当种群内fmax-fmax>δ时,表面种群内部适应度较为集中,应增大pc,提升搜索进度,求解最优解,同时增大pm,增加产生新个体的速率,增强种群的多样性。
(2)SA在优化过程中能够弥补GA在局部寻优时的不足。
文中选取指数退火方式进行降温操作,即:
Ti=T0ki-1
(10)
式中,Ti为当前退火进行的温度;k为衰减系数;T0为初始温度。
在此基础上,提出一种在初始解附近,随机邻域拓展以产生新解的机制,即:
(11)
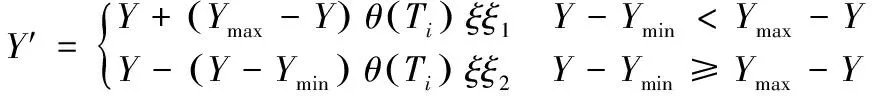
(12)
式中,Y′为新解;Y为当前解;Ymax,Ymin为Y所在种群内的最大解和最小解;ξ,τ为[0,1]内均匀分布的随机数;θ(Ti)为扰动函数;ξ1,ξ2为[0,0.1]内均匀分布的随机数。
合理选用随机邻域拓展机制,既能全面搜索初始解的领域,又能保障新解的质量。Y是否变为Y′,可采用Metropolis准则进行判断,Metropolis准则如下所示:
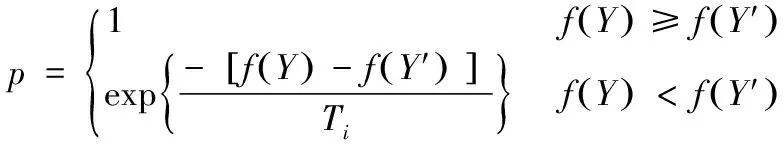
(13)
使用Metropolis准则判断时,若Y′较优,则接受新解为当前解。若新解Y′较劣,则以概率p判断是否接受新解。
3.3 自适应GA-SA算法基本步骤
步骤1:设置种群规模N、最大进化代数Mmax、初始退火温度T0、最小温度Tmin和温度衰减系数k等初始参数;
步骤2:初始种群以随机方式生成,计算种群内个体适应度值,并对个体进行选择、交叉、变异操作,其中按照等式(8)计算是否交叉,按照等式(9)计算是否变异,生成适应度最佳的个体;
步骤3:对SA寻找到的适应度较大的个体,计算其适应度值并进行模拟退火操作,θ(Ti)按照等式(11)计算,对当前解按照等式(12)进行解的变换。比较新解Y′与当前解Y的适应度值,使用Metropolis准则判断是否采用新解,若采用,则以新解替换当前解,否则,以概率P接受新个体,舍弃旧个体;
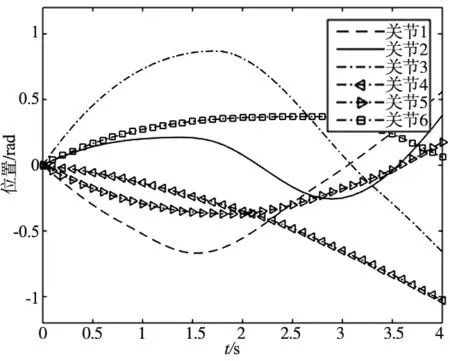
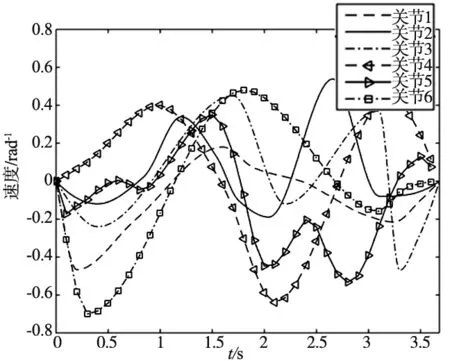
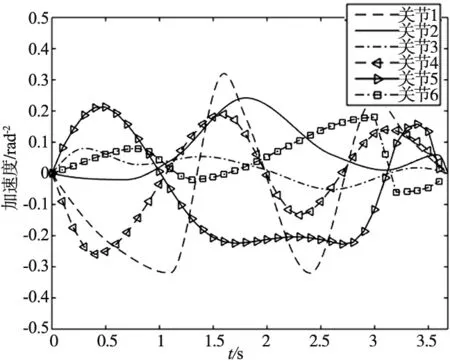
步骤4:判断当前进化代数gen是否小于最大进化代数Mmax,若gen 步骤5:判断当前温度T是否小于最小温度Tmin,若T 自适应GA-SA算法流程图如图4所示。 图4 自适应GA-SA算法流程图 在MATLAB平台下分别选用10维、30维、50维测试函数进行计算,验证自适应GA-SA算法优化性能,其结果如图5~图7所示。 图5 10维测试函数 图6 30维测试函数 图7 50维测试函数 由上图可知,算法采用自适应方法与邻域拓展以产生新解机制,在测试函数计算下,算法初期阶段适应度曲线迅速向最佳适应度曲线靠近,收敛速度较快,具有跳出局部最优的能力。自适应GA-SA算法既能全面搜索初始解的领域,又能保障新解的质量,确保算法全局优化性能。 文中以PUMA762为验证对象,采用ADAMS绘制虚拟样机模型,如图8所示。合理设置相关参数后,依据机械臂结构模型图绘制机械臂运行轨迹,如图9所示。设置第一段轨迹运行时间为1 s,第二段轨迹运行时间为2 s,第三段轨迹运行时间为1 s,起始点、终止点的速度加速度均为0。 (a) 虚拟样机模型 (b) 机械臂运行轨迹图8 虚拟样机模型与运行轨迹 在提取各关节运行轨迹点后,使用自适应GA-SA进行优化设计,经优化后得到第一段轨迹最优时间为0.893 s,第二段轨迹最优时间为1.875 s,第三段轨迹最优时间为0.932 s,总体运行时间为3.68 s。经优化后的机械臂位置曲线、速度曲线、加速度曲线如图9所示。 (a) 位置曲线 (b) 速度曲线 (c) 加速度曲线图9 位置、速度、加速度曲线 由上图可知,经优化后的机械臂速度曲线、加速度曲线光滑连续,运行平稳,满足运动学、动力学约束。合理运用自适应GA-SA算法提升了串联机械臂各关节轨迹运行的连续、稳定性,切实完成运行轨迹时间优化,提高工作效率,具有实际意义。 文中提出一种自适应遗传模拟退火算法,借助MATLAB工具箱绘制PUMA762串联机械臂运行轨迹,结合ADAMS虚拟样机模型设置运行时间等相关参数后,通过自适应遗传模拟退火算法进行时间最优化设计,使得工作时间由4 s优化为3.68 s。 (1)遗传算法设计时采用自适应方法,使得pm值与pc值随适应度函数变化而改变,保障优化前期,具有较强的全局搜索能力,优化后期,确保新个体的产生。 (2)模拟退火算法设计时,选取指数退火方式进行降温操作,并提出在初始解附近,随机邻域拓展以产生新解的机制,既能全面搜索初始解的领域,又能保障新解的质量。
3.4 函数测试
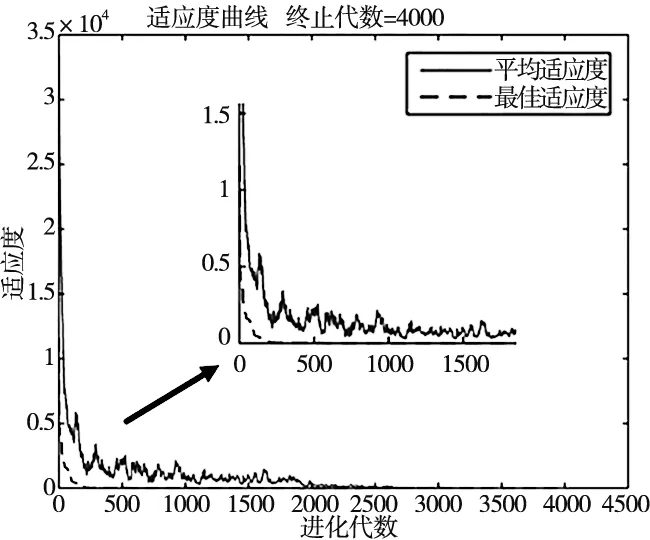
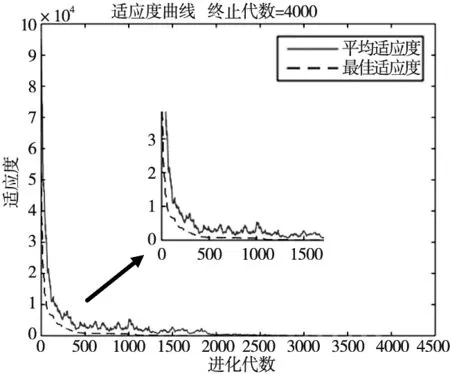
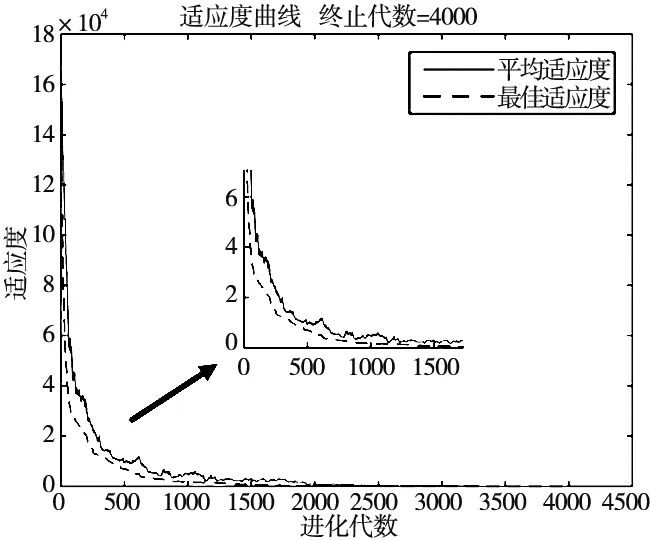
4 仿真验证

5 结论
