基于梯度提升的多标签分类器链方法

王 进，陈 瑀，孙开伟

(重庆邮电大学 数据工程与可视计算重点实验室，重庆 400065)

多标签学习(multi-label learning)不同于传统的每个实例对应一个标签的单标签学习问题，它是一种每个实例可能同时关联多个标签的监督学习问题.多标签的应用受到越来越多的关注，它适用于各种领域，包括文本分类[1-2]、场景和视频分类[3]以及生物信息学[4]等.

问题转换法是多标签分类的常见方法之一，它将多标签问题转换成一个或多个单标签(即二分类或多分类)问题.以这种方式，就可以采用单标签分类器将单标签的预测转化成多标签的预测.问题转换法具有可扩展性和灵活性，具体表现在：任何现成的单标签分类器都可以用于这种方式的多标签分类.问题转换法的代表方法是二元相关法(binary relevance,BR)[5].BR将多标签问题转化为多个二元问题，每个标签训练一个二分类模型.但BR经常被忽视，因为它不能有效利用标签之间存在的关联性.而以分类器链方法(classifier chains,CC)[6]、集成分类器链方法(ensembles of classifier chains,ECC)[6]为代表的分类器链方法兼具效果与灵活的优点.ECC可以对标签关联性进行建模，并且采用了机器学习中的“集成”的思想来提高分类精度.它们都具有接近BR方法的复杂度，在考虑标签关联性的诸多方法中，具有较大优势.但是CC方法存在严重的链序问题，以及标签关联性感知不足等问题，而ECC存在着随机性较大、链序问题未完全消除等问题.

针对目前多标签分类所关心的标签关联性问题以及分类器链方法的链序问题，文中提出基于梯度提升的多标签分类器链方法(gradient boosting classifier chain,GBCC).在GBCC中，每一个层次都维护一个标签集合，对于集合中每一个标签进行梯度提升过程，并在此过程中通过计算误差评价分数以及标签置信度来进行特征传递，建立标签之间的关联.GBCC模型通过梯度提升与标签评价分数解决链序问题并挖掘高阶标签关联性，并综合各层次的预测信息作为最终的结果.

1 相关工作

1.1 梯度提升方法

在机器学习领域中，提升(boosting)[7]方法是一种常见的集成学习方法，应用十分广泛.在分类问题中，它通过改变训练样本的权重学习多个分类器，并将这些分类器进行线性组合，提高分类的性能.通常，这种提升的思想被用到回归问题中，因为当采用平方误差损失函数时，一般只需要简单地拟合当前模型的残差，而将其用于分类问题则显得不那么容易.在梯度提升决策树(gradient boosting decision tree,GBDT)[7]方法中就讨论过这个问题，其说明了对分类问题采用提升方法的合理性和有效性.因此，文中可以合理地对多标签分类问题采用提升方法，所需要拟合的残差即为真实概率与预测概率之差.

1.2 多标签学习方法

多标签学习按照方法的不同可以分为问题转换法和算法适应法.BR是最普通的问题转换方法，理论上简单直观，由于它不考虑标签关联性，因此对过度拟合标签组合具有很强的抵抗力.由于标签与二分类模型具有一对一的关系，因此可以添加和删除标签而不影响模型的其余部分.与其他方法相比，BR最重要的优势就是其低计算复杂度，代表方法包括BR、CC、ECC等.二元成对分类方法(binary pairwise classification,PW)[5]是一种将标签两两组合并针对每对标签训练二分类模型的问题转换法，其在模型数量方面与标签数量成平方关系，校准标签排名(calibrated label ranking,CLR)[5]方法即为PW方法的代表方法.标签组合方法(label combination,LC)[5]是一种仅涉及单个模型的问题转换法，它通过将每一种标签组合视为一个类别从而转化为多分类问题.但LC最坏情况下的类别数量随标签数量呈指数级增长，一切模拟所有标签集的方法都必然会遇到这种复杂性，例如随机标签集合方法(randomk-labelsets,RAKEL)[5].

算法适应法是一种通过改进方法以适应多标签数据的方法.多标签k近邻(multi-labelk-nearest neighbor,ML-kNN)[5]方法的基本思想是让k近邻方法适应于多标签数据，其中最大后验准则用于推理包含在近邻中的标签信息.多标签决策树(multi-label decision tree,ML-DT)[5]方法的基本思想是采用决策树方法来处理多标签数据，其利用基于多标签熵的信息获取准则来递归地构建决策树.增量式超网络学习方法(hierarchical multi-label classification using incremental hypernetwork,HMC-IMLHN)[8]通过将超网络的超边组织成相应的层次结构，使输出的预测标签能够满足标签的层次约束.

1.3 分类器链方法

对于标签集合L，BR的|L|个二分类问题是独立的，其无法对标签进行相关性建模.J.READ等[6]提出了一种新颖的二元相关方法CC，它可以对标签相关性进行建模，同时保持与BR类似的可接受的计算复杂度.CC涉及|L|个二分类模型，因此CC也是二元相关方法，但它与BR的不同之处在于每个二分类模型的特征空间用先前所有分类器的预测结果进行相关性扩展，从而形成分类链.尽管向每个实例添加了平均|L|/2个属性，但是标签空间L的大小始终受到限制，因此CC的计算复杂度可以非常接近于BR的计算复杂度.然而CC的链序问题却使其预测效果大打折扣.J.READ等[6]又提出了可以解决链序问题的ECC方法，它训练多条CC分类器链，每条链被赋予随机链序，并且在随机选择的N个训练实例上进行训练.ECC利用了机器学习中集成方法的思想，提高了分类精度，并且让复杂度依然保持与BR相当.尽管ECC在一定程度上解决了链序问题，但是其存在随机性，会造成分类效果不稳定.概率分类器链(probabilistic classifier chains,PCC)[9]旨在解决错误传播问题，尽管PCC与CC具有相同的学习模型，但它通过穷举搜索最大后验概率来选择最佳预测变量，穷举产生的指数级开销限制了它的应用.贝叶斯分类器链(bayesian classifier chains,BCC)[10]引入了有向树作为标签上的概率结构.通过随机选择标签作为其根，并为其余边缘分配方向来建立有向树.它与CC共享相同的模型，但是将父标签的数量限制为不超过1，这限制了BCC在标签相关性上的表达能力.优化分类器链(optimization of classifier chains,OCC)[11]及其集成方法(ensembles optimization of classifier chains,EOCC)[11]则是从条件似然最大化的角度优化分类器链，主要从标签关联性和多标签特征选择等两个方面进行，但是其依然存在着分类器链随机与分类效果不稳定等问题.文中方法也是一种集成多标签分类器链方法，但是与上述方法不同，文中方法在一个整体上构建多个分支进行梯度提升过程，建立起标签间的高阶关联性，在层次上计算误差评价分数来决定最优链序，具有与CC方法相当的复杂度与灵活性，可提升分类性能与分类效果的稳定性，具有更广泛的适用性.

2 基于梯度提升的多标签分类器链

2.1 符号定义

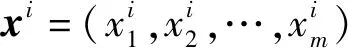
2.2 GBCC整体框架

图1是文中方法的训练与预测框架图.

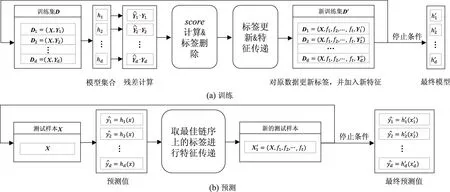
图1 GBCC训练和预测框架

预测阶段将测试样本输入第1层基分类模型，获得预测值yi，然后取最佳链序上的预测值进行特征传递，获得新的测试样本，不断迭代直到满足停止条件，最后综合各层次的预测结果作为最终的输出结果.

为了进一步阐明本方法的思想，给出一个方法示例如图2所示.

图2 在具有5个标签数据集上的方法示例

在图2中，以5个标签的数据作为示例，原始标签集合L={l1,l2,l3,l4,l5}，假设计算出各个标签置信度为C={0.30,0.20,0.20,0.35,0.05}，输入阈值r0=0.005.第1层的当前标签集合为ε={l1,l2,l3,l4,l5}.为每个标签训练一个基模型，然后计算出各个模型的训练误差r，假设r={0.30,0.01,0.10,0.35,0.02}，再计算出score={1.00,0.84,0.91,1.00,0.97}.此时训练误差都没有低于阈值，不做处理.l2的评价分数为其中的最小值，在当前标签集合中删除l2，此时ε={l1,l3,l4,l5}.用l2的预测结果扩展特征空间，因此下一层的各个模型的输入特征空间维度由m扩展到m+1.在后一层采用前一层对应标签的输出作为新的标签值，继续训练.迭代，直到当前标签集合ε为空.对各层次的模型进行线性组合即得到最终输出模型.图2中空心圆的标签链即为找出的最优链序.

2.3 分类器链方法的扩展

分类器链方法是一种高效的多标签分类方法.而提升方法是一种机器学习集成方法，它们有一个共同点就是模型的串行训练.因此本文的核心就是基于梯度提升对分类器链方法进行改进，旨在通过提升过程和误差评价分数，提高标签关联性与模型稳定性，增强预测性能.GBCC方法主要包括两部分：误差评价、梯度提升.此方法的输入：训练集D，标签集合L，阈值；输出：集成模型fM(x).其流程如下：

计算出每一个标签li的置信度ci

while |ε|==k,k>0

fori=1 tokdo

训练回归模型fi(x)

计算训练误差ri，评价分数scorei

end for

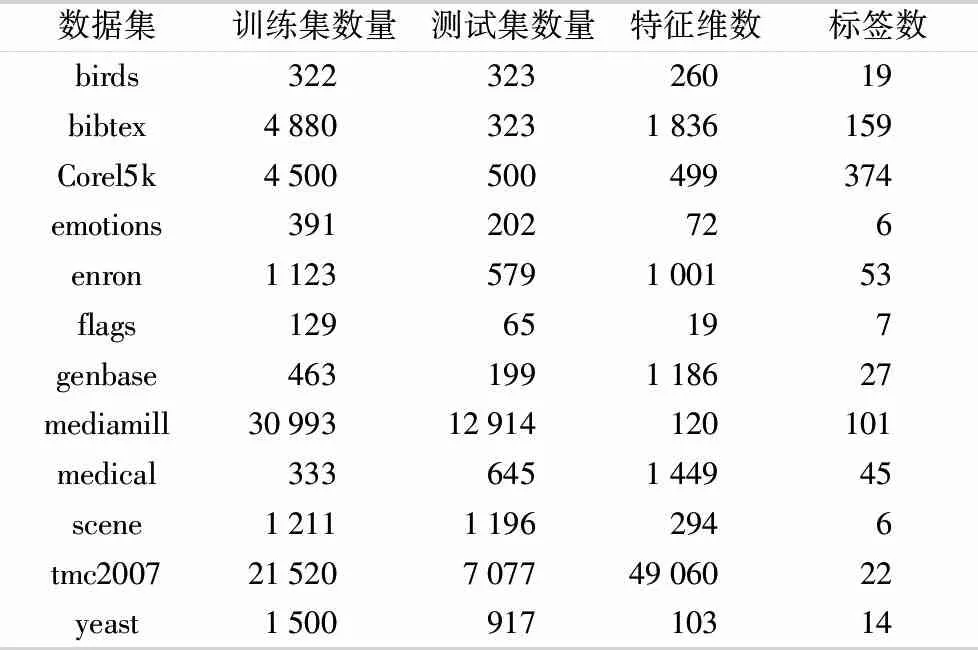
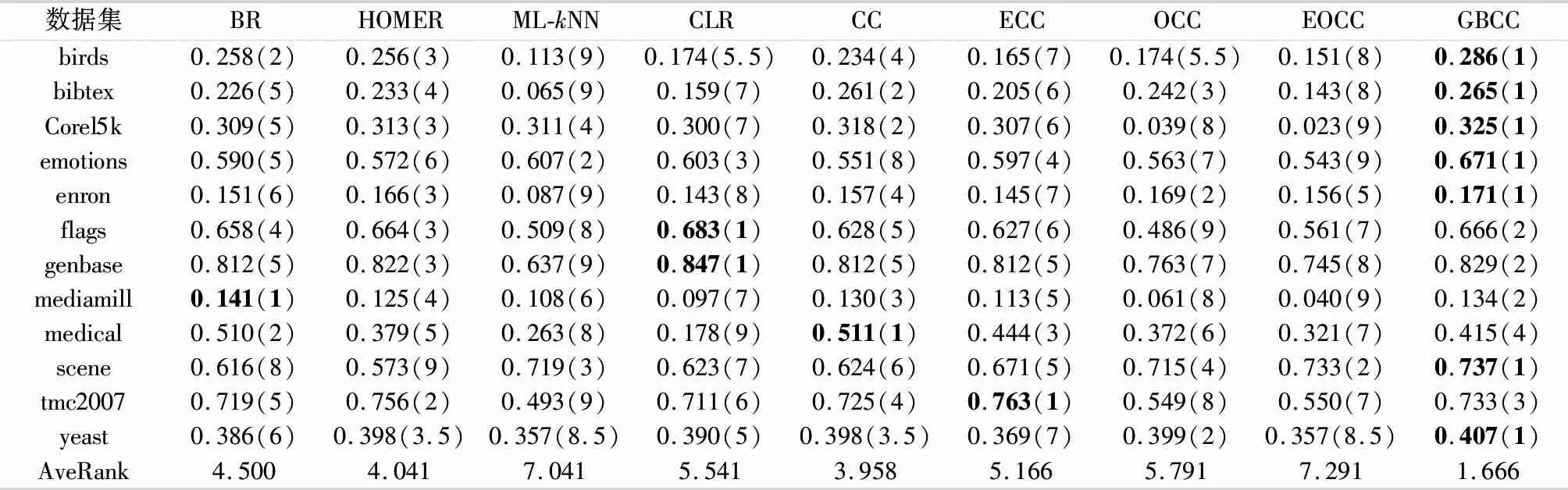
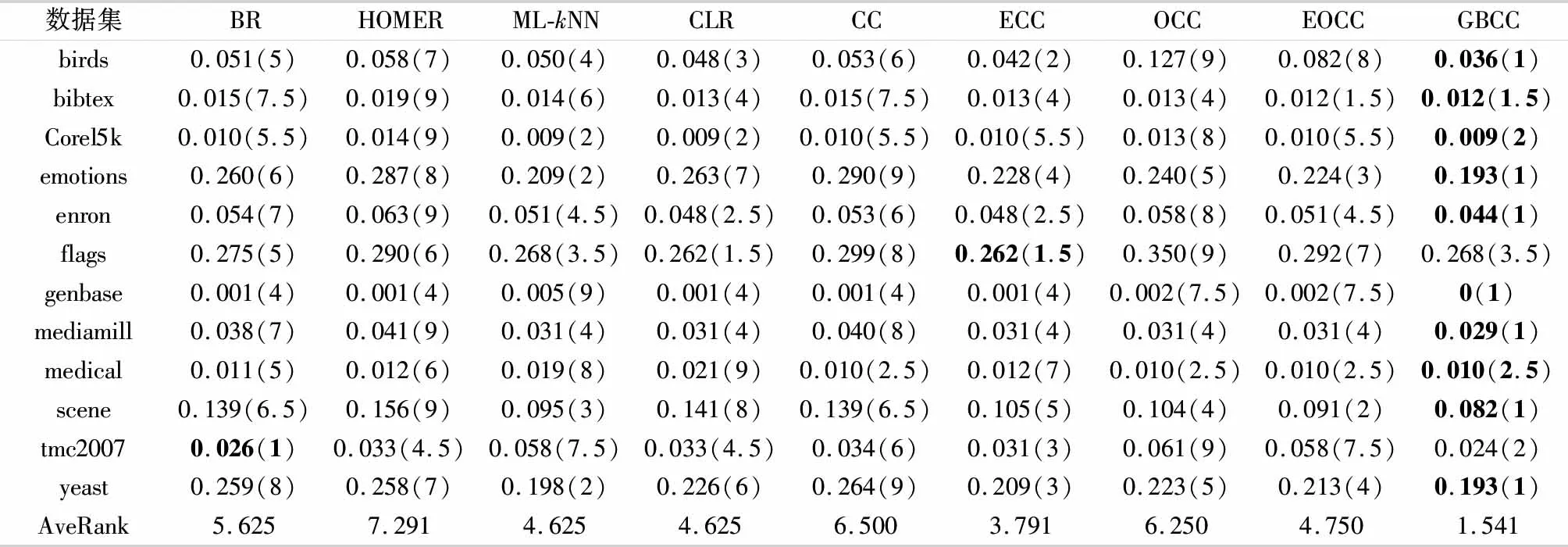
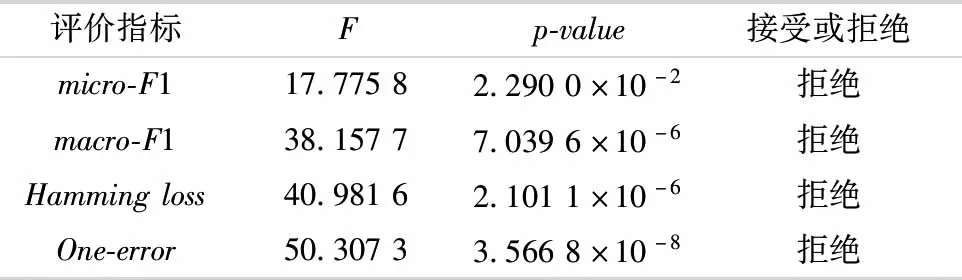
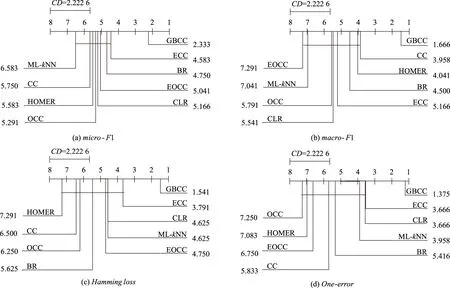
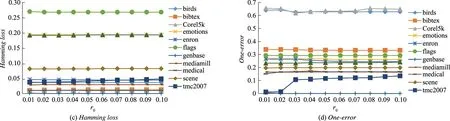
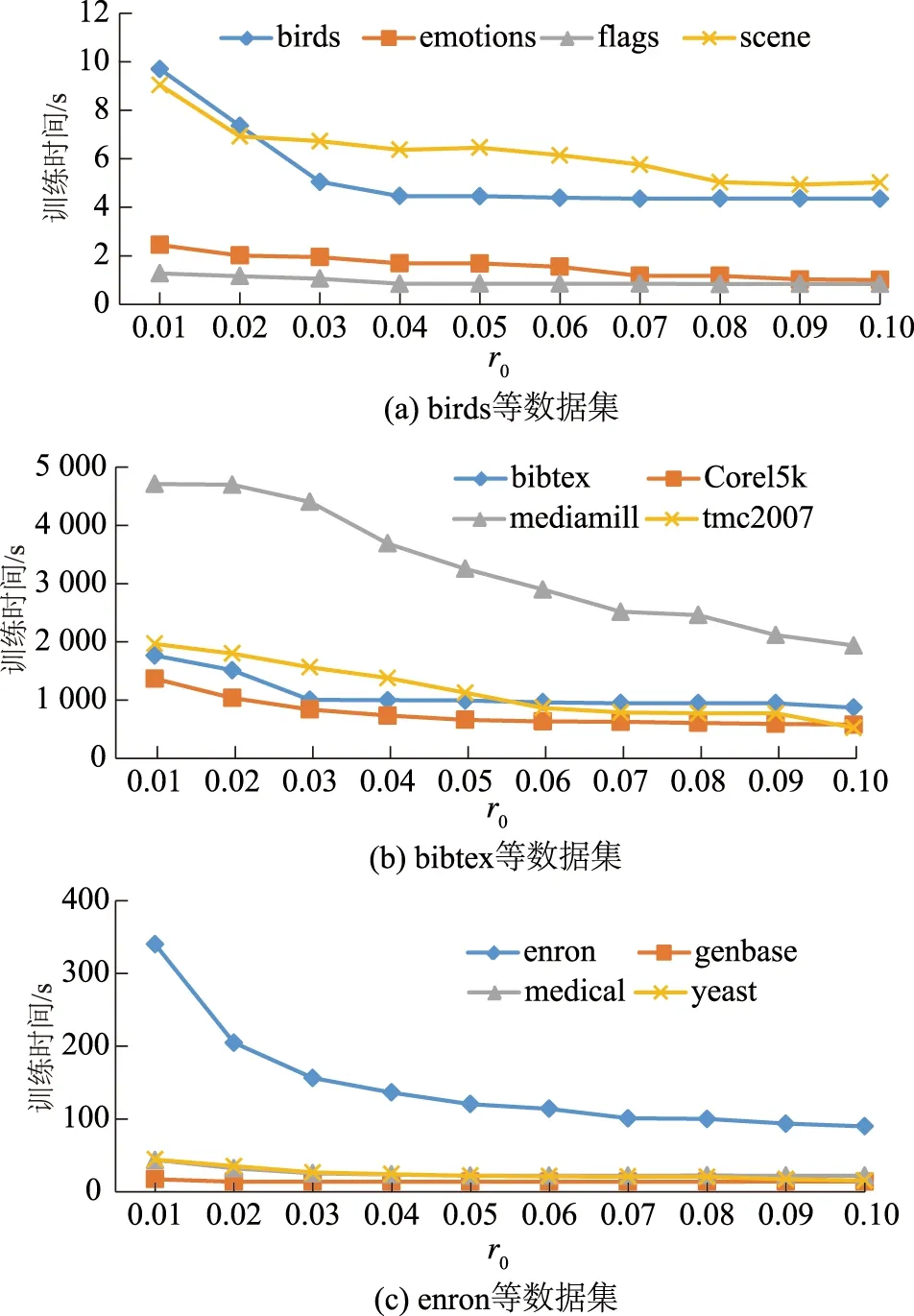
在ε中删除li,其中ri

用最优fi(x)扩展数据集D的特征空间

用各个标签的残差更新D对应标签的值

end

2.3.1预剪枝策略

预剪枝策略通过计算误差评价分数来进行，误差评价即对当前已经训练好的模型进行评估，旨在找出分类效果最佳的标签作为当前层的最佳预测变量.其具体过程如下：

1) 给出原始标签集合L，计算出每一个标签li的置信度ci，其中i∈1,2,…,|L|,li∈L，即每个标签的样本数在全部样本数中的占比.通过计算标签置信度，表征标签的分布情况，即

ci=Dli/D.

(1)

2) 维护一个标签集合ε作为当前层的标签集合.为ε中的每一个标签训练一个目标值为0～1的回归模型.然后计算出每一个模型的训练误差ri(均方误差)，通过与设定的阈值r0进行比较，若标签对应模型的训练误差小于等于该阈值，则在当前标签集合ε中删除该标签.这是一种预剪枝的策略，起到了防止过拟合与加速训练的目的.

3) 综合训练误差ri与标签置信度ci计算出对标签预测效果的评价分数，即

scorei=ri+1/(ci+1).

(2)

当训练样本中标签分布不同时，样本数量较少的标签的训练误差可能出现过拟合，即样本较少的标签训练误差不足以评判它的真实性能.而该评价分数值则加入了对于数据真实分布的考量，使得评判分数更加可信.分子分母同时加1是为了防止ci为0而导致计算错误.找出score最小的标签，将其预测值作为新的特征扩展到特征空间，此时Rm扩展为Rm+1，即更新原始数据集D为D′.最后在当前标签集合中删除该标签，表示该标签可以不用继续训练，防止过度拟合.

2.3.2梯度提升

基于梯度提升的分类器链方法旨在通过梯度提升方法增强单个标签上的预测性能.在某一分支(标签)上，进行一个梯度提升过程，其基本过程如下：

1) 初始化一个基模型f0(x).

2) 对于m=1,2,…,M，i=1,2,…,N，利用损失函数H的负梯度在当前模型的值

(3)

即残差，拟合一个回归模型T(x;θm).

3) 更新当前模型：

fm(x)=fm-1(x)+T(x;θm),m=1,2,…,M.

(4)

4) 最后通过线性组合得到输出模型：

(5)

2.4 复杂度分析

多标签问题转换方法通常从标签复杂度的角度进行复杂度分析.针对标签集合L，在理想情况下，GBCC训练完第1层就停止，即GBCC退化为BR方法.此时，方法的标签复杂度为O(|L|)，其中|L|表示标签数量.而在最坏的情况下，GBCC的结构完全展开，其将会训练|L|+(|L|-1)+(|L|-2)+…+1，即[(|L|+1)|L|]/2个基模型，因此最坏情况下方法标签复杂度为O(|L|2).表1给出了不同分类器链方法的对比.

表1 分类器链方法对比

如表1所示，文中方法的理论标签复杂度并不具有明显优势，但是在训练过程中加入的评价机制与剪枝策略，使得训练开销能够接近其他集成分类器链方法.GBCC在保持了和其他分类器链方法相近的训练开销的同时解决了链序问题与结果稳定性问题.

3 试 验

3.1 试验设置

为了验证GBCC能够有效挖掘利用高阶标签关联性、解决链序问题并提升预测性能，文中选择了4个分类器链相关方法(CC、ECC、OCC、EOCC)和4个其他种类多标签方法(BR、层级多标签分类方法(hierarchy of multi-label classifiers,HOMER)[5]、ML-kNN、CLR)在12个多标签数据集上进行了比较.

在本试验中，BR、HOMER、ML-kNN、CLR、CC、ECC这几个方法的源码来自Mulan多标签学习开源项目(http:∥mulan.sourceforge.net/datasets-mlc.html)，其参数为Mulan中的推荐参数.OCC、EOCC采用方法原文提供的源码(http:∥github.com/futuresun912/oCC)实现.所有的数据集均来自Mulan的数据库，且已经被划分为训练集和测试集，它们各自的特点总结在表2中.

表2 数据集详情表

3.2 评估指标

多标签分类模型预测性能的评价指标按照考察的方面可以分为两类：一类是基于实例的分类精度;另一类是基于标签的排名.HammingLoss[5]、micro-F1[5]、macro-F1[5]为第1类，One-error[5]为第2类.其中，micro-F1、macro-F1值越大表示分类越准确，以↑表示；而HammingLoss、One-error值越小表示分类越准确，以↓表示.

3.3 试验结果与分析

3.3.1验证方法的预测精度

GBCC与其余对比方法的预测结果如表3-6所示.其中，最优结果加粗表示，AveRank表示方法结果的平均排名.

表3 各个方法在不同数据集上的micro-F1值↑

续表

表4 各个方法在不同数据集上的macro-F1值↑

表5 各个方法在不同数据集上的Hamming loss值↓

表6 各个方法在不同数据集上的One-error值↓

为了体现出文中方法与其他对比方法的显著性差异，针对各个评价指标的结果使用Friedman[12]检验.首先提出假设H0：这9种多标签分类方法没有显著性差异.表7是在各个评价指标下Friedman检验的结果信息，其中数据集12个，对比方法9个，显著性水平为0.05，F为Friedman卡方统计量.

表7 Friedman检验结果

由表7可见，由于p-value值都小于0.05，因此在各个评价指标下都拒绝原假设H0，说明了GBCC与其他比较方法之间在预测性能上存在显著性差异.

在对这9种对比方法进行了整体上的差异性分析之后，由于“这9种多标签分类方法没有显著性差异”这个假设被拒绝，则说明方法的性能显著不同，还需要进一步地比较方法两两之间的差异性，采用Bonferroni-Dunn检验作为事后多重检验post-hoc test[12].首先需要计算出平均序值差别的临界值域(critical difference,CD)[12]，其计算式为

(6)

式中：k为比较的方法数量，k=9；N为数据集数量，N=12.通过查表可知在显著性水平∂=0.05时，q∂=1.988，因此CD=2.222 6.从图3可以看出GBCC在各个评价指标下的预测性能都显著优于其他方法.

图3 各指标下9个对比方法的平均排名

3.3.2参数分析

对于文中方法GBCC，阈值r0是一个重要的参数，为了研究r0的敏感度，r0以0.01为步长，从0.01到0.10的范围对方法GBCC进行试验.如图4所示，分别在各个评价指标下展示了GBCC在不同数据集中不同r0值下的变化情况.

图4 不同数据集的各指标随r0的变化情况

由图4可见，有部分数据集在某些指标上随着r0的变化性能产生了明显变化，但是大部分呈现平稳的趋势.可见，在大部分数据集下r0的变化对于预测性能来说并不敏感.

图5是不同数据集的训练时间随r0的变化情况.

图5 不同数据集的训练时间随r0的变化情况

由图5可见，随着r0的增大各个数据集的训练时间都整体呈现下降趋势.其中数据集Corel5k、emotions、enron、mediamill、tmc2007、yeast在r0的变化区间上呈现持续的下降，而其余几个数据集呈现出先下降后平稳的趋势，结合本方法的特点分析，造成这一现象的原因主要在于当r0增大到一定程度的时候本方法退化为了BR方法，因此当r0继续增大的时候训练时间基本保持不变.通过以上分析可知：参数r0对于预测性能不够敏感，但是它对于降低训练时间起着重要作用.可以在保持预测性能相当的前提下，通过增大r0来降低训练开销.

4 结 论

文中针对多标签分类器链方法的标签关联性表达不足，存在链序等问题，基于梯度提升提出一种改进的分类器链方法.在12个不同规模且属于不同领域的数据集上的试验结果表明，本方法具有良好的预测性能.并且通过参数分析发现超参数r0对于训练的时间开销十分敏感，说明超参数r0改善了原始数据分布带来的影响并且有效降低了训练开销，起到了防止过拟合以及保持方法灵活性的作用.