频率-贝塞尔变换方法在巢湖滩涂浅层勘探上的应用
2021-05-28戴文杰王建楠杨振涛陈晓非
戴文杰, 潘 磊, 王建楠, 杨振涛, 陈晓非
(1.中国科学技术大学 地球和空间科学学院,合肥 230026;2.深圳市深远海油气勘探技术重点实验室(南方科技大学),深圳 518055;3.南方科技大学 地球与空间科学系,深圳 518055)
0 引言
近地表地震面波勘探方法分为主动源方法和被动源方法。主动源方法包括MASW方法[1];变换方法[2];倾斜叠加法[3];高分辨率拉东变换方法[4]。相对于主动源勘探,背景噪声成像方法具有成本低、对周围环境无影响、不需要人工震源和可随时采集的优点。被动源勘探方法的代表是SPAC方法,由Aki[5]提出;Okada等学者[6-11]又将其进行了扩展,简化了观测点的布局,提出了三分量数据处理方法,改善高阶频散信息的利用等。但该方法主要用于提取面波的基阶频散曲线。越来越多的研究表明,高阶频散曲线对约束成像结果的非唯一性、提高成像质量至关重要[12-16]。因此,提取高阶面波频散曲线无论对主动源还是被动源面波成像方法都十分重要。陈晓非等[17-19]提出了基于观测阵列的频率-贝塞尔变换方法(F-J方法)。该方法对波场资料做频率-贝塞尔变换,得到频散能量图,图中极大值点就构成了频散曲线。该方法既可以用于主动源的观测资料[19],也适用于背景噪声的互相关资料[18-20]。
笔者采用基于噪声互相关资料的被动源方法处理巢湖滩涂采集的背景噪声数据,提取出了清晰的基阶和一阶频散曲线,并进行了联合反演,得到了测点下方60 m深度内的速度结构信息。结果表明,频率-贝塞尔变换方法在浅地表勘探中是行之有效的。
1 被动源的F-J方法原理
地表距离为r的两个台站同一时间段的噪声记录的频率域互相关函数C(r,ω)近似为格林函数的虚部,二者仅在幅值上存在差异[21],因此有:
C(r,ω)≈A·Im{Gzz(r,z=0,ω)}
(1)
其中:A为常量;Gzz(r,z=0,ω)为地表格林函数的垂直分量。
根据王建楠等[17]给出的F-J方法,可以得到:

(2)

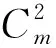
2 数据处理和分析
2.1 数据采集
本次数据采集点在合肥巢湖长临河镇南部滩涂,如图1所示。实验场地靠近巢湖边,离场地较远处有较为密集的居民楼和长临河镇中心。场地附近地形较为开阔平坦,起伏较小,便于仪器安放,符合背景噪声数据采集的基本要求。使用了三分量地震仪,虽然可以得到三个分量的数据,但在实际处理数据时,我们只需要用到垂向Z分量。本次实验一共使用了39个台站,同步采集时长是30 min,采样率为200 Hz。F-J方法对台站布置并没有严格限制,理论上越均匀随机越好。本次采集台站分布呈一定弯曲的曲线,台站间距约2 m,x方向展布约68 m,y方向展布约6.5 m。
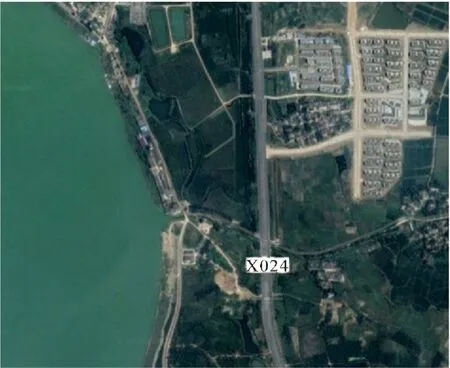
图1 巢湖滩涂场地卫星图片Fig.1 Satellite image of Chaohu beach site
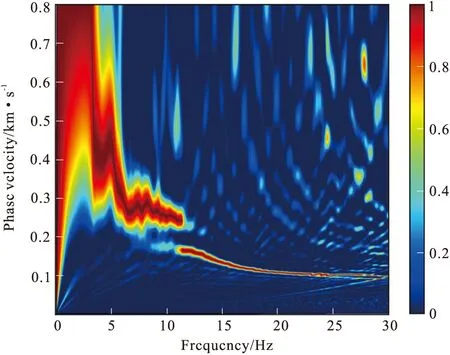
图2 叠加后的频率相速度谱Fig.2 Superimposed frequency phase velocity spectrogram
2.2 数据处理和提取频散曲线

单次扫描结果往往不够理想,通常采用时间域叠加的方式来放大频散曲线能量,同时压制和抵消干扰,以达到提高频散图像分辨率的目的。我们的做法是将扫描得到的频散谱中分辨率较高的时间段进行叠加求平均(图2)。由图2可以看到,叠加后频散曲线连续且清晰,易于辨别,有利于反演时准确提取频散点。图2中,基阶和1阶能量比较大,在25 Hz ~30 Hz这样的高频区域,仍能看到明显的基阶频散曲线。
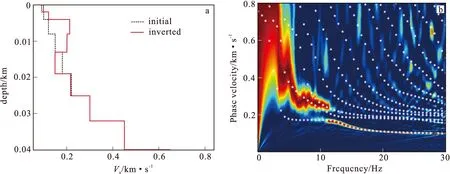
图3 只用基阶的反演结果Fig.3 Inversion results only using the fundamental mode(a)反演的S波速度结构;(b)用反演结果计算得到的理论频散曲线和实际频散曲线拟合图

图4 不同初始模型下只用基阶的反演结果Fig.4 Inversion results only using the fundamental mode with different initial velocity model(a)反演的S波速度结构;(b)用反演结果计算得到的理论频散曲线和实际频散曲线拟合图
从图2可以看到,频散曲线在低频呈“之”字型,这是目前工程勘探应用中经常会遇到的情况,也被称为面波多模态现象,是基阶和高阶联合作用的结果[23-24]。出现这种现象是因为当存在低速层或者高速层的时候,瑞利波各模式的能量分布会随之发生变化,各模态的速度也会随频率变化而改变,在频散曲线上表现为频散曲线相互靠近,形成“模式接吻”(osculation)。如果某一频段内高阶振型能量占优,那么该频率范围内只能看到高阶面波,而无法得到基阶面波,此时必须使用基阶和高阶面波联合反演才能降低不确定性。
2.3 地下速度结构的反演
在得到了频散曲线后,采用拟牛顿法进行反演。先采用8 Hz~25 Hz的基阶频散曲线来反演。为了对比初始模型的影响,使用了2种不同的初始模型,分别对应图3和图4。图3 (a)是反演得到的速度结构,由于只利用了基阶高频信息,因此只能得到0 m ~20 m内的结果,更深的结构需要低频信息才能反演得到。图3 (b)是用反演得到的速度模型计算的理论频散曲线和实际频散曲线的拟合图。反演结果表明,仅用基阶面波频散信息来反演,对S波速度反演提供的约束太少,只能得到浅部结构信息,得到的地下速度结构不够准确。
为了验证高阶频散曲线对反演浅部精细结构能提供有效约束,使用与图4相同的初始模型,并联合使用基阶和1阶频散点的信息进行反演,结果如图5所示。从图5可以看出,在结合了1阶频散信息后,反演深度从只用基阶的20 m左右提高到近50 m。不仅深度提高了许多,而且不同深度的S波速度都比初始模型要高。S波速度随着深度呈现阶梯分层式增加,符合巢湖滩涂沉积层地质构造的特点。对比图5(b)和4(b),在联合了1阶频散信息后,两者吻合程度有所提高。从图5(b)中可以看到,在4 Hz和13 Hz附近基阶和高阶曲线比较贴近,通过前面的分析我们知道,当地下速度结构出现低速或者高速的时候,不同阶的频散曲线会发生“模式接吻”。由于实际地层经常会发生地层缺失和嵌套的情况,因此“模式接吻”经常发生。我们的结果也验证了这一点。
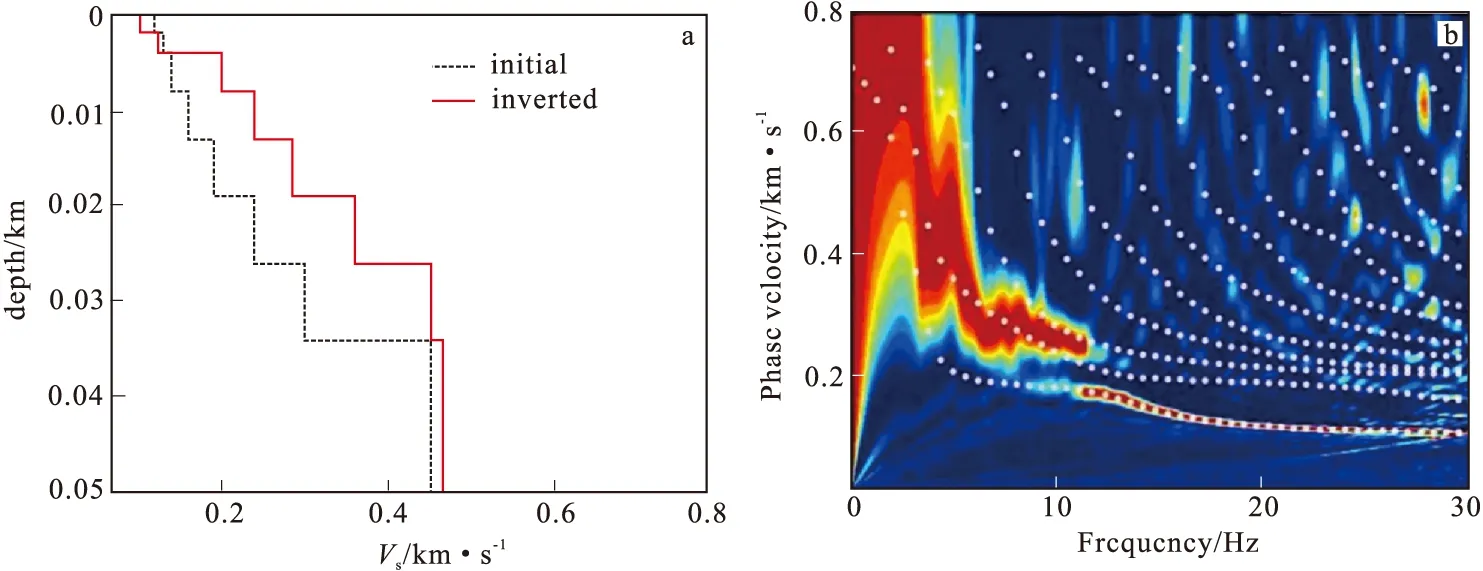
图5 联合基阶和1阶的反演结果Fig.5 The results of the fundamental and first mode joint inversion (a)反演得到的地下速度结构;(b)反演结果得到的理论频散曲线和实际频散曲线的叠加对比图

图6 测点附近的地质钻孔剖面图Fig.6 Geological borehole profile near survey point
为了检验反演结果的可靠性,用测点附近的钻孔数据做参考,如图6所示。从图6中可以看出,存在地层缺失和嵌套的情况,反演得到的地层速度变化也符合场地实际情况。
这一效果的提高,证明了高阶信息在浅层结构勘探中能起到有效的约束,同时也说明频率-贝塞尔变换方法提取的高阶模式的信息是真实有效的。
3 结论
将F-J方法应用到安徽合肥巢湖滩涂场地的浅层勘探中,利用实际采集的背景噪声数据,采用F-J方法提取了面波的基阶频散曲线,得到了基阶和1阶频散曲线,而且基阶和1阶出现了面波模态叠加。对比了只用基阶频散信息和采用基阶、1阶频散曲线联合反演这两种情况,结果表明,1阶频散信息的使用对浅层精细结构的反演提供了更强的约束,得到的结果更加精细,反演深度更深,从而验证了频率-贝塞尔变换方法在实际浅层勘探中是可行的、有效的。
