基于透射光谱的类金刚石膜光学参数反演

王贵全，张锦荣，邵 毅，郑万祥，唐莹娟，胡 中，姜兴平，李彦生,，李 伟，王乔方，字正华

〈材料与器件〉

基于透射光谱的类金刚石膜光学参数反演

王贵全1，张锦荣2，邵 毅1，郑万祥3，唐莹娟3，胡 中3，姜兴平1，李彦生1,3，李 伟3，王乔方3，字正华3

（1. 昆明北方红外技术股份有限公司，云南 昆明 650217；2. 中国人民解放军32228部队，福建 厦门 361000；3. 昆明物理研究所，云南 昆明 650223）

本文采用透射光谱法测量Ge基底类金刚石薄膜（Diamond-like carbon，DLC）的光谱曲线。应用测量的光谱曲线，基于模拟退火算法，构建目标优化函数，通过光谱反演法得到薄膜的厚度、折射率、消光系数。该方法得到的Ge基底类金刚石膜的光学参数与椭偏仪测试结果比对，折射率误差小于1%，厚度误差小于2%。并且将薄膜的光学参数带入透过率理论计算模型，得到的Ge基底类金刚石薄膜透射光谱曲线和实际测试曲线的误差小于2%。该方法只需测量透射光谱曲线，通过计算就能得到薄膜光学参数，对光学薄膜设计和加工具有重要指导意义。

类金刚石薄膜；透射光谱；薄膜厚度；折射率；消光系数

0 引言

类金刚石薄膜（diamond-like carbon, DLC）具有较高的硬度，抗摩擦性强，耐腐蚀性能好，能够满足不同的使用环境对镀膜元件的不同要求，它被广泛应用于各个领域。

薄膜光学常数是描述光与物质相互作用的重要物理量，是入射光频率的函数[1]，膜制备过程中，薄膜光学依赖薄膜镀制工艺方法和制备过程，不同的镀制工艺得到的薄膜光学常数各不相同。精确测量薄膜光学常数数值对膜系设计和实际应用十分重要[2-3]。

目前，薄膜光学常数的测试方法包括非光学测量方法与光学测量方法[4]两大类。非光学测量方法包括a粒子法、超声波法等，主要适用于对光学特性依赖程度不高的薄膜。光学测量方法主要有光度测量法[5]、椭偏法[6-7]、外差干涉法[8]、棱镜耦合法[9]、光谱反演法[10]等。目前常用的光谱反演法包括包络线法[11]、K-K法[12-13]、全光谱拟合法[14]等。本文借助Cauchy色散模型[15]，采用透射光谱法对类金刚石薄膜样品进行测试，通过模拟退火算法[16]，构建目标优化函数，利用自编的Matlab算法，得到薄膜的厚度、折射率、消光系数。

1 算法模型

1.1 透过率理论计算模型

如图1所示，对于镀类金刚石膜的平行平面零件，为便于讨论计算，把薄膜视为质地均匀、各向同性的等厚膜。

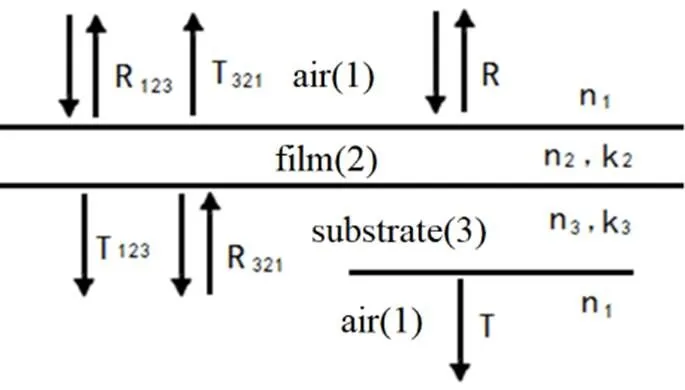
图1 光在均匀弱吸收表面的透射和反射

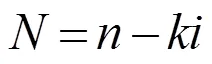
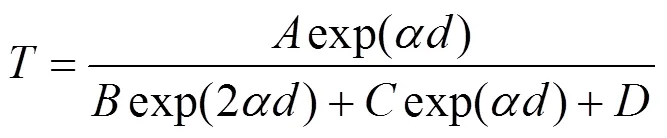
式中：

式中：为位相角；为基底的吸收因子；为基底第2个界面的反射率；s是基底的透射率，对透明基底有＝1，3＝0。

由(1)式可知，透射率是波长、薄膜光学常数的函数，＝(1,2,2,,3,3,)，若1、3，3，均已知，此时透过率就是薄膜光学常数2，2，的函数，可表示为：

＝(2,2,) (2)

1.2 色散模型

薄膜折射率和吸收系数是随波长变化的，Ge基底类金刚石薄膜在2.5～12mm波段属于透明弱吸收薄膜。一般介质薄膜材料的光学常数都满足Cauchy色散模型，可采用Cauchy色散模型拟和类金刚石薄膜光学常数。

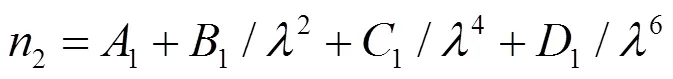
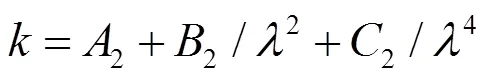
由(2)、(3)、(4)可得：

此时，计算整个波段内的薄膜光学参数的问题就转化为求解(5)式的问题。

1.3 光学常数与透过率的关系

从理论透射率计算公式(1)可以看出，、、不是互相独立的。图2、图3、图4分别给出了Ge基底类金刚石膜薄膜的不同折射率、不同消光系数、不同薄膜厚度条件下透过率与波长之间的关系。

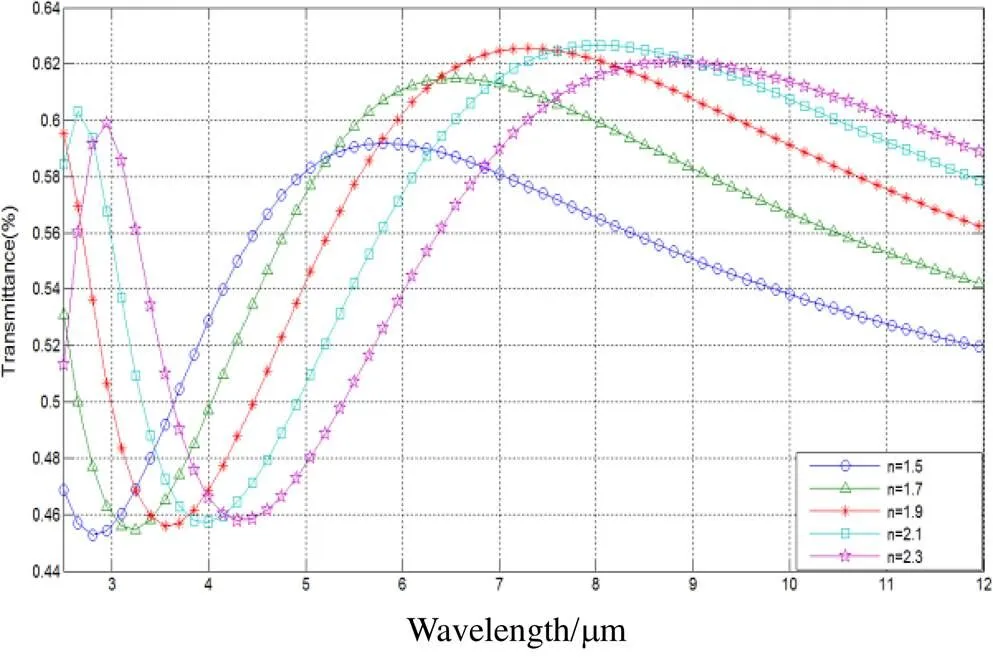
图2 膜层不同折射率下波长与透过率变化曲线

1）膜层折射率与透过率的关系

已知1＝1，1＝0，2＝0.01，3＝4.003，3＝0.01，＝950nm。图2给出了折射率2不同时波长与透射率之间的关系图。从图中可以看出，随着薄膜折射率的增加，透射峰逐渐向长波方向移动，峰值透过率由小逐渐变大，再逐渐变小。

2）膜层厚度与透过率的关系

已知1＝1，1＝0，2＝2.1，2＝0.01，3＝4.003，3＝0.01。图3给出了不同薄膜厚度（）条件下波长与透射率之间的关系图，从图中可以看出，随着薄膜厚度的增加，透射峰逐渐向长波方向移动。

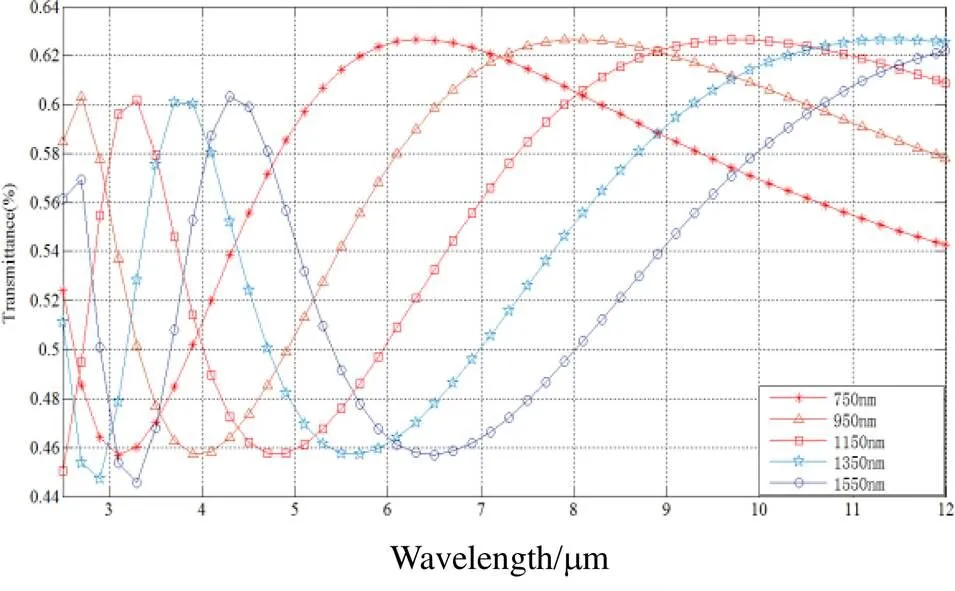
图3 膜层不同厚度下波长与透过率变化曲线

3）膜层消光系数与透过率的关系

已知1＝1，2＝2.1，＝950nm，3＝4.003，3＝0。图4给出了薄膜不同消光系数条件下波长与透过率之间的关系，从图中可以看出，随着值的增加，峰值透过率逐渐降低，前端次峰的峰值透过率降低更明显。

从以上的分析可知：消光系数主要影响透过率，随着值的增加，透过率逐渐降低。随着薄膜折射率的增加，透射峰逐渐向长波方向移动，峰值透过率由小逐渐变大，再逐渐变小。随着薄膜厚度的增加，透射峰逐渐向长波方向移动。

2 模拟退火算法

本文利用模拟退火算法反演求解薄膜光学参数，将“评价函数”替代系统的能量，用“待求参数的变化”替代退火过程中分子的移动，用“优化迭代过程中的步长”等效温度的变化速度，如果在优化过程中让迭代步长缓慢变化，并且以某种概率随机运动，就有可能获得一个最小的目标函数值，即达到了该优化问题的全局最优解。式(5)中，波长和透过率是通过红外光谱仪测量得到的基本参量，求解(5)式的问题就变成根据已知的测量值求解非线性方程组。如以最小二乘法计算值与实际测量值之间的逼近程度作为判断，则评价函数为：

式中：为选取的计算值的点数；Tc为计算值；Tm为实际测量值。

3 实验及结果

3.1 实验样品制备

实验样品基底材料选用Ge材料，对其表面进行两面抛光，在其中的一面镀制类金刚石膜，另一面不镀膜。样品两面的加工指标如下：

光圈＝0.2，局部光圈D＝0.1，样品两面的平行度＝10²。

3.2 样品透射光谱测试

镀膜完成之后，采用傅里叶红外光谱仪测试Ge基底类金刚石膜试验样品的透射光谱曲线，测试波长范围2.5～11mm，透射光谱曲线如图5所示。

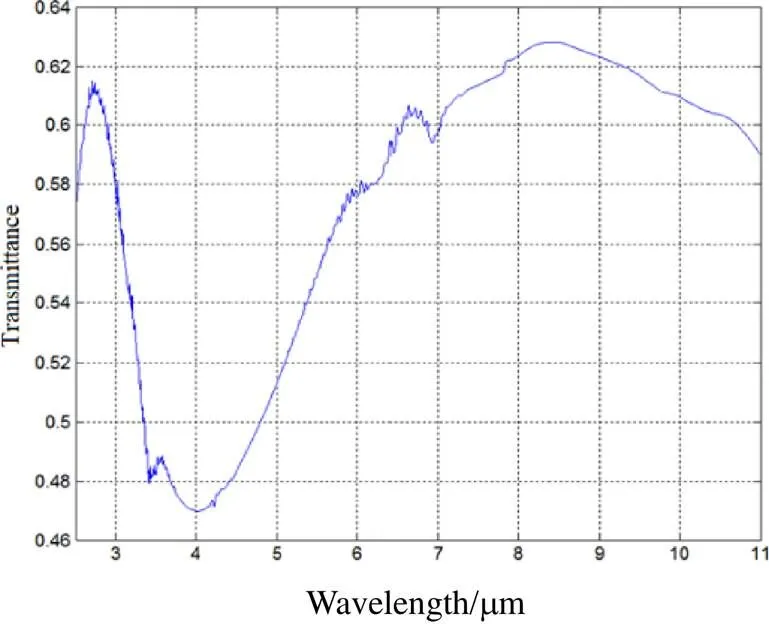
图5 Ge基底类金刚石膜透射光谱曲线

3.3 模拟退火算法计算膜层折射率和厚度

由Metropolis等[17]提出并发展起来的模拟退火算法因其在全局范围内有极强大的搜索能力而被广泛应用于诸多领域。

本文采用模拟退火算法求解非线性方程组＝(1,1,1,12,2,2,,)。由于Ge基底类金刚石膜在2.5～11mm波段范围的消光系数一般在10－3量级，根据菲涅尔公式可知，薄膜折射率的作用远大于消光系数的影响。所以在应用模拟退火算法确定薄膜参数时，仅考虑了薄膜折射率对透过率的作用。因而＝(1,1,1,1,,)非线性方程组有5个值需要计算，故必须从光谱曲线上选取5个测量值m1，m2，m3，m4，m5。如以最小二乘法对计算值与实际测量值之间的逼近程度作为判断，则评价函数为：

＝(c1－m1)2＋(c2－m2)2＋(c3－m3)2＋

(c4－m4)2＋(c5－m5)2(7)

式中：下标c，m分别表示计算值和实际测量值；越小，说明测量值和计算值越接近，的最小值对应待求的参数值，即方程的解。模拟退火算法流程图如图6所示。

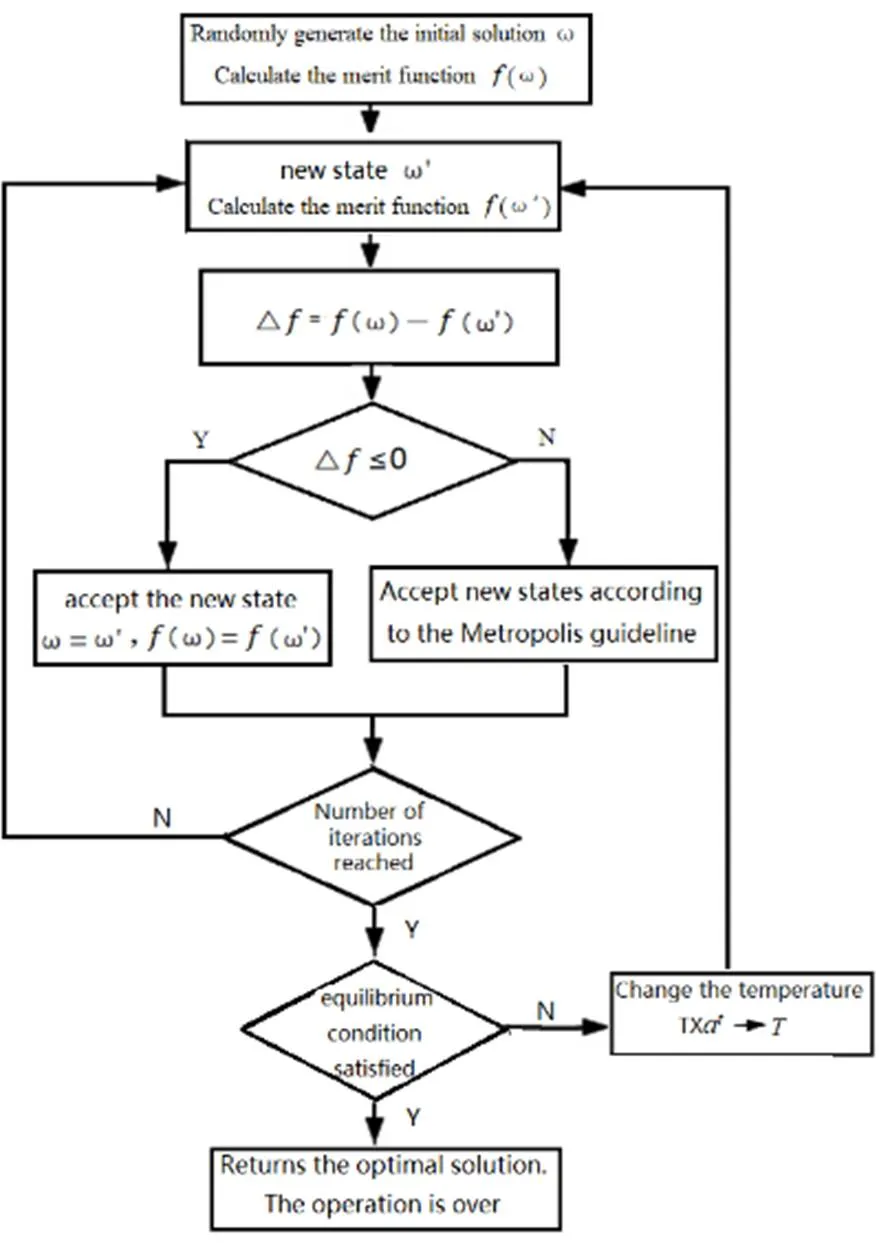
图6 模拟退火算法流程图

4 拟合结果与误差分析

4.1 拟合结果

采用模拟退火算法结果如下：

1＝2.00008，1＝0.3362，1＝－1.1534，1＝0.5579，＝998nm。

采用Matlab编程方法绘制图形，得到薄膜2.5～11mm波段Ge基底类金刚石膜折射率色散曲线如图7中虚线所示。

为了验证算法的正确性，采用J. A. Woollam公司VASE型椭偏仪对实验样品进行测试（椭圆偏振法测量确定薄膜参数时，假定薄膜具有理想的光学表面，薄膜折射率不随厚度变化），得到类金刚石膜折射率曲线如图7中实线所示（薄膜厚度＝1018nm）。

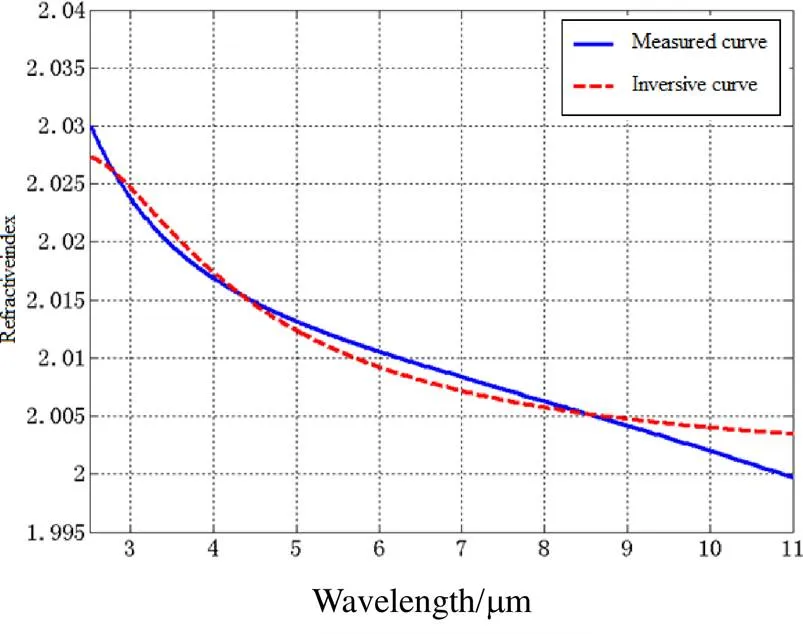
图7 模拟退火算法反演与椭偏仪测试结果对比图

Ge基底类金刚石膜厚度相对误差：

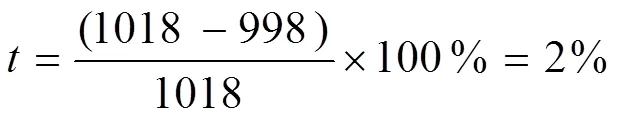
根据模拟退火算法得到的光学常数，可重新计算得到薄膜2.5～11mm波段Ge基底类金刚石膜的透射光谱曲线，其模拟退火算法得到的结果与实测透射光谱曲线的对比结果，如图8所示。

4.2 误差分析

从图7可以看出，尽管在求解过程中做了近似计算（如假设所求解的光谱区内吸收系数为零）。但并没有因此带来很大的误差，且在所求解的区域内精度很高。应用该方法计算Ge基底类金刚石薄膜的光学常数，折射率反演结果与椭偏仪[18-19]测试结果比对，误差小于1%。膜层厚度反演结果与椭偏仪测试结果比对，误差小于2%。

由此可见，采用正常色散特征的Cauchy模型能够准确表征Ge基底类金刚石膜2.5～11mm波段的吸收特性。

从图7可以看出，透过率理论计算模型得到的Ge基底类金刚石薄透射光谱曲线和实际测试曲线的相对误差小于2.5%。这表明通过模拟退火算法得到的光学常数能够较准确地描述Ge基底类金刚石膜实际透射率的变化规律。

该方法只需测试透过率曲线，通过计算就能够得到薄膜光学参数，对光学薄膜设计和加工具有实际应用价值。

5 结论

采用基于透射光谱的模拟退火算法得到的类金刚石薄膜光学常数与椭偏仪的测试结果符合度较高。拟合得到的类金刚石膜透射曲线与实测曲线基本吻合。因此，通过模拟退火算法得到的Ge基底类金刚石薄膜光学常数能够较准确地描述类金刚石薄膜实际透过率的变化规律，可为膜系设计提供依据。同时，该方法只需测试透过率曲线，通过计算就能够得到薄膜光学参数，具有测试过程简单、计算收敛速度快、精度高等优点，对光学薄膜设计和镀制具有重要指导意义。

[1] 李建超, 苏俊宏, 徐均琪. 类金刚石薄膜光学常数拟合模型的合理性研究[J]. 应用光学, 2004, 25(5): 56-59.

LI Jiachao, SU Junhong, XU Junqi. Study of the reasonableness of fitting model concerning DLC film optical constant[J].., 2004, 25(5): 56-59.

[2] 章睿荣. 通过全光谱拟合法确定薄膜光学常数和厚度[D]. 杭州: 浙江大学, 2007.

ZHANG Ruirong. Determination of Optical Constants and Thickness of Thin Film with Whole Optical Spectrum Fitting[D]. Hangzhou: Zhejiang University, 2007.

[3] 李国龙, 钟景明, 王立惠, 等. 反射光谱拟合法确定聚合物半导体薄膜光学常数和厚度[J]. 激光与光电子学进展, 2016, 53(4): 043101.

LI Guolong, ZHONG Jingming, WANG Lihui, et al. Determination of optical constants and thickness of polymer semiconductor thin film with reflectivity fitting method[J]., 2016, 53(4): 043101.

[4] 乔明霞. 薄膜光学常数和厚度的透射光谱法测定研究[D]. 成都: 四川大学, 2006.

QIAO Mingxia. Study on Determination of Optical Constants and Thickness of Thin Films by Transmission Spectrum Method[D]. Chengdu: Sichuan University, 2006.

[5] 张奇志. 单层SiN衰减型相移掩膜研究[D]. 成都: 四川大学, 2001.

ZHANG Qizhi. Study of the Attenuatal Phase Motion Coating of SiN[D]. Chengdu:Dectoral Thesis, Chengdu: Sichuan University, 2001.

[6] Jakopic G, Par G, Papoueek W. Unified analytical inversion of reflectometric and ellipsometric data of absorbing media[J]., 2000, 39(16): 2727-2732．

[7] 陈燕平, 余飞鸿. 薄膜厚度和光学常数的主要测试方法[J]. 光学仪器, 2006, 28(6): 84-88.

CHEN Yanping, YU Feihong. Test methods for film thickness and optical constants[J]., 2006, 28(6): 84-88.

[8] Chiu M, Lee J, Su D. Complex refractive-index measurement based on Fresnel′s equations and the uses of heterodyne interferometry[J].. 1999, 38(9): 4047-4052

[9] 杨天新, 邹豪, 王雷, 等. 棱镜耦合法确定条形波导的渐变折射率分布[J]. 中国激光, 2010, 37(3): 689-695.

YANG Tianxin, ZOU Hao, WANG Lei, et al. Determining the graded -index profiles of channel wave guides by prism coupling method[J]., 2010, 37(3): 689-695.

[10] 周天宇. 光学薄膜反演软件的研制与应用[D]. 长沙: 国防科学技术大学, 2010.

ZHOU Tianyu. Design and Application of Software of Reverse Engineering of Optical Coating[D]. Changsha: National University of DefenseTechnology, 2010.

[11] 夏志林, 薛亦渝, 赵利, 等. 基于包络线法的薄膜光学常数分析[J]. 武汉理工大学学报: 信息与管理工程版, 2003, 25(5): 73-76.

XIA Zhilin, XUE Yiyu, ZHAO Li, et al. Analysis of thin film's opticalparameters based on the envelope method[J].: Information & Management Engineering, 2003, 25(5): 73-76.

[12] 李凯朋, 王多书, 李晨, 等. 光学薄膜参数测量方法研究[J]. 红外与激光工程, 2015, 44(3): 1048-1052.

LI Kaipeng, WANG Duoshu, LI Chen, et al. Study on optical thin filmparameters measurement method[J]., 2015, 44(3): 1048-1052.

[13] Laaziza Y, Bennouna A, Chadburn N. Optical characterization of lowoptical thickness thin films from transmittance and back reflectance measurements[J]., 2000, 372: 149-155.

[14] 侯典心, 路远, 宋福印. 基于全光谱拟合法的VO2薄膜光学常数计算[J]. 红外技术, 2017, 39(3): 243-249.

HOU Dianxin, LU Yuan, SONG Fuyin. Optical constants of VO2thin films based on whole optical spectrum fitting[J]., 2017, 39(3): 243-249.

[15] 闫威. 某些非线性色散方程的确定性与不确定性[D]. 广州: 华南理工大学, 2011: 28-35.

YAN Wei. Certainty and Uncertainty of Some Nonlinear Dispersion Equation[D]. Guangzhou: South China University of Technology, 2011.

[16] 阳生红, 余招贤, 李辉道, 等. 模拟退火法在椭偏光谱数值反演中的应用[J]. 红外与毫米波学报, 2000, 19(5): 338-342.

YANG Shenghong, YU Zhaoxian, LI Huidao, et al. Simulated annealing optimization algorithm for inverting ellipsometric spectra[J]., 2000, 19(5): 338-342.

[17] Kirkpatrick, S Gelatt, C D Vecchi, M P Kirkpatrik S, et al. Optimization by using simulated annealing[J]., 1983: 671-680.

[18] 徐均琪, 冯小利. 多层薄膜光学常数的椭偏法研究[J]. 光电工程, 2009, 36(2): 29-33.

XU Junqi, FENG Xiaoli. Optical constants of multi-layer thin films investigated by spectroscopic ellipsometry[J]., 2009, 36(2): 29-33.

[19] 余平, 张晋敏. 椭偏仪的原理和应用[J]. 合肥学院学报: 自然科学版, 2007, 17(1): 87-89.

YU Ping, ZHANG Jinmin. The principle and application of ellipsometery[J].: Natural Sciences Edition, 2007, 17(1): 87-89.

Calculation of Optical Parameters of Diamond-like Carbon Film Based on Transmission Spectrum

WANG Guiquan1，ZHANG Jinrong2，SHAO Yi1，ZHENG Wanxiang3，TANG Yingjuan3，HU Zhong3，JIANG Xinping1，LI Yansheng1,3，LI Wei3，WANG Qiaofang3，ZI Zhenghua3

(1. Kunming North Infrared Technology Co. Ltd, Kunming 650217, China; 2.Unit 32228 of the Chinese People’s Liberation Army, Xiamen 361000, China; 3. Kunming Institute of Physics, Kunming 650223, China)

In this paper, transmission spectroscopy was used to measure the spectral curve of Diamond-like carbon film on Ge substrate. By using the measured spectral curve and simulated annealing algorithm, the objective optimization function was constructed, and the thickness, refractive index and extinction coefficient of the film are obtained by spectral inversion. Compared the optical parameters of Diamond-like carbon film on Ge substrate obtained by this method with the measured results of ellipsometer, the error of refractive index is less than 1%, the error of thickness is less than 2%. In addition, the optical parameters of the film were brought into the theoretical calculation model of transmittance. Compared with the actual measured curve, the error of the transmission spectrum curve of Diamond-like carbon film on Ge substrate is less than 2%. Once the transmission curve measured, the optical parameters of the film can be obtained by calculation.

DLC film, transmission spectral, film thickness, refractive index and extinction coefficient

O635.1

A

1001-8891(2021)05-0473-05

2020-01-13；

2020-02-21.

王贵全（1981-），男，高级工程师，主要从事红外材料特性与光电系统集成技术研究。E-mail：119455225@qq.com。