计算机网络中脆弱节点快速定位方法的设计与实现

李 庐

(安徽财经大学教务处，安徽蚌埠 23303)

0 引言

当前无线传感器网络(Wireless Sensor Networks，WSN)在各领域具有较高的应用价值.因为物联网中的WSN节点部署环境存在较高的随机性，并且节点容易产生故障，导致WSN网络的运行质量降低.因此，寻求有效的物联网中的WSN网络中的节点故障定位方法，成为相关人员分析的热点.伴随经济环境的快速发展，国外的基于物联网的信息化战略项目发展速度较快，比如说u-Korea、u-Japan[1，2]，物联网也被列入我国战略性新兴产业予以重点扶持，为了构建物联网，就需要找准网络节点，快速定位脆弱节点，而国内关于脆弱节点的快速定位方法研究起步较晚，且缺乏技术创新与机制创新，在此类问题研究上，较国外项目仍存在一定差距.不同功能的微型传感器，以及不同的计算机网络，所得到的监测效果不尽相同，如何利用有限的计算量实现对目标区域的监测是研究的难点，快速定位计算机网络中的节点位置，是当前节点研究中的重点问题，本文通过将计算机中的脆弱节点进行定位，使网关连接到Internet，再利用其它网络基础设施，实现对目标区域的监测.

1 计算机网络中脆弱节点快速定位方法

1.1 建立计算机网络中的脆弱节点模型

在探究计算机网络中脆弱节点快速定位方法时，首先对计算机网络中的节点模型进行建立，在模型的基础上对快速定位方法进行探究.脆弱节点包含已知节点、未知节点，以及待定位节点，实际建立网络定位的节点数学模型时，需要3个节点同时存在，才能建立出相应的脆弱节点模型.为此设置计算机网络中共有a个脆弱节点，其中存在一部分未知节点.为了对网络中的脆弱节点模型进行建立，可以采用斜率值与斜率差进行信息处理.基于斜率值与斜率差，设置已知节点的二维坐标为m；设置未知节点的二维坐标为n，m与n的关系可用下图1来表示.

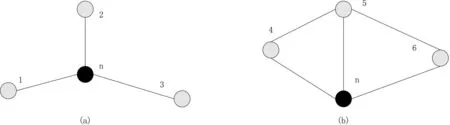
图1 二维节点平面图Fig.1 2D node plan

在图1中，空心节点为已知节点，用数字1～6表示，实心节点n为未知节点[3].在图(a)中，已知节点1、2、3的位置时，能够求出未知节点n的位置；在图(b)中，三个已知节点4、5、6除了与未知节点相连，还以平面展开的方式，连接了相近节点，且已知节点间的连线趋近于一条直线，此时很容易产生误差的测距，进而无法求解出未知节点n.综上所述，(a)图所表示的模型建立方式相对完善，便于后续研究，采取此种节点排列方式将模型建立完毕.

1.2 选择脆弱节点的最优组合

在具备节点模型的基础上，以三个m节点不共线的方式，表示节点间的共存关系，为了减少了脆弱节点的构建成本，以及定位时产生的能量消耗，需要进一步筛选脆弱节点的最优组合.在计算机网络中，主要选用非测距的定位算法，去计算未知节点与已知节点间的真实距离，路径覆盖度的高低，对整体的测量环节有着决定性作用，网络的整体定位精度也与节点的实际位置存在关系.在出现超过三个已知节点的情况时，需要判断三个节点是否处于一条直线上，有以下公式：

x=(ms+ns)x+nsu

(1)

根据上述公式(1)判断三个节点是否处于一条直线上，若在一条直线上将无法对节点位置进一步求解.采用平面几何中的斜率，对已知节点与未知节点间的位置关系进行推算，确定最优脆弱节点组合，在分析待定位节点的过程中，准确确定未知节点的位置[4].在计算机网络中，当未知节点接收到已知节点的数据信号时，进而判断网络中的节点数量，其中已知节点、未知节点与待定位节点间的分布关系如下图2所示.

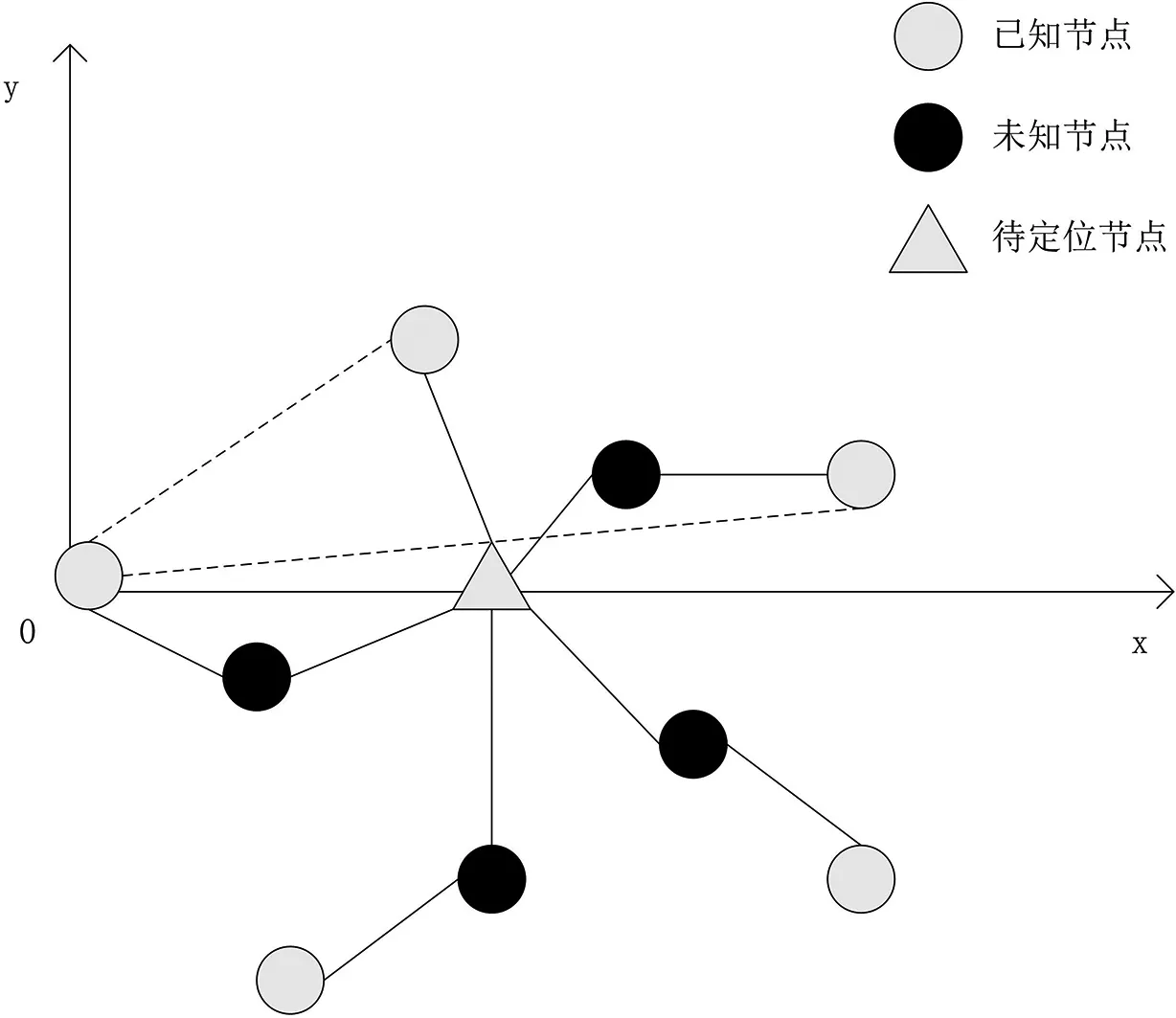
图2 脆弱节点间分布关系图Fig.2 Distribution diagram of vulnerable nodes

如图2所示，各个已知节点不处于一条直线，为了测量待定位节点的位置，需要选取距离未知节点最近的已知节点信息，并以此作为推算过程的参考节点，然后在剩余已知节点中选取两个其他

节点，并将其作为定位节点[5].构成3个已知节点之后，判断这3个节点是否存在共线情况，因为在算法的初始化阶段，计算机中的数据信息会随着时间不断移动跳跃，而在采取斜率判断法时，通过反复推算3个已知节点是否共线，得到最优的脆弱节点组合，为实现节点间的快速定位打下基础[6].

1.3 推算脆弱节点位置的变化次数

在具备节点模型与脆弱节点的最优组合之后，针对计算机网络中产生的节点位移变化，对其中位置的变化次数进一步求解，将其抽象成求解函数方程的类似问题，在构建节点间非线性方程之后，对相应时间内的脆弱节点间位置变化次数，展开具体推算.在实际网络中，节点间的位置变化具有迭代效应，可以将其转化为求解函数方程的过程，此类方程的计算公式为：

f(q)=0

(2)

其中，f(q)为代数多项式，其零点表示为q，在求解脆弱节点位置的变化次数时，可将其表示为变化次数，当其为一元一次函数方程时，求解此方程的过程较为简单；当其处于物理学领域时，需要将其转化为非线性方程组，采用非线性的函数求解方式，解决此类问题.选取一个近似值作为节点位置的初始值，采用一个递推公式对其多次校正，此时递推公式为：

qn+1=φ(qn),k=0,1,...,n

(3)

在上式(3)中，k为两个节点间连线的斜率，取值为自然数，采用此迭代法对迭代次数进行求导，可得序列公式为：

(4)

根据公式(4)，可以得到在网络变化下，节点位置的相对次数变化趋势.

1.4 构建脆弱节点快速定位方程

为进一步快速定位计算机网络中脆弱节点，需要在已知时间与变化次数的基础上，对定位方程进行构建.在网络的定位区域中，已知节点的同步运转，能够带动所有节点进行时钟同步运转，这种节点的变化方式，使得整体网络具备统一性效果，在实际定位中，已知节点的数量是有限的，因为已知节点需要带动未知节点，所以其所具有的能量相对较大，根据两种节点之间的距离，也会存在不同的信号差，一般来说，在相同时间内，距离越短的两个节点信号强度越高，相距越远的两个节点信号越弱，利用脆弱节点之间的距离，能够实现对其的快速定位[7].在节点模型中，设已知节点1与未知节点n之间的距离为r1，基于计算机网络下脆弱节点位置的变化次数，此时r1的计算公式为：

(5)

在上式(5)中，X1为节点1的横坐标，Y1为节点1的纵坐标；x为未知节点n的横坐标，y为未知节点n的纵坐标.

同理可得已知节点2与未知节点n之间的距离为r2，此时r2的计算公式为：

(6)

在上式(6)中，X2为节点2的横坐标，Y2为节点2的纵坐标；x为未知节点n的横坐标，y为未知节点n的纵坐标.

已知节点3与未知节点n之间的距离为r3，此时r3的计算公式为：

(7)

在上式(7)中，X3为节点3的横坐标，Y3为节点3的纵坐标；x为未知节点n的横坐标，y为未知节点n的纵坐标.

在一定时间内，对节点变化所产生的实际运转距离进行求导，可得推算公式为：

(8)

在上式(8)中，R为节点变化所产生的实际运转距离，在此基础上，构建脆弱节点快速定位方程，可将其表示为：

(9)

在公式(9)中，f(x,y)为未知节点n的位置坐标，在已知其它节点坐标，与节点实际运转距离的基础上，可以完成对未知节点n快速定位方程的构建，进而实现对其的快速定位[8].

2 实验研究

2.1 实验准备

为了分析研究方法在实际定位时能获得更小的误差，特将计算机网络中脆弱节点快速定位方法作为实验组，选取两种传统方法作为实验对照组，设计仿真实验研究，验证在不同方法的应用下，对计算机中的voronoi多边形进行构建，进而分析不同定位方法下的脆弱节点定位误差[9].

选取三个相同配置的计算机作为实验对象，将它们放置在同样的网络环境中，进行对比实验研究.为了更好地验证设计方法的误差度，可以采用网络拓扑结构进行实验研究，并将其配置在三台计算机中.选用20 m×20 m的网络拓扑，进行多边形区域定位，在计算机网络的定位空间中，将节点无线射程设置为30 m，在不同的定位区域下，设置锚节点数目分别为5和10，如下图3所示.对节点定位误差分析时，当网络中节点定位误差结果无限大时，此时产生的定位精度为100%.一切设置妥当无问题后，展开测试实验.

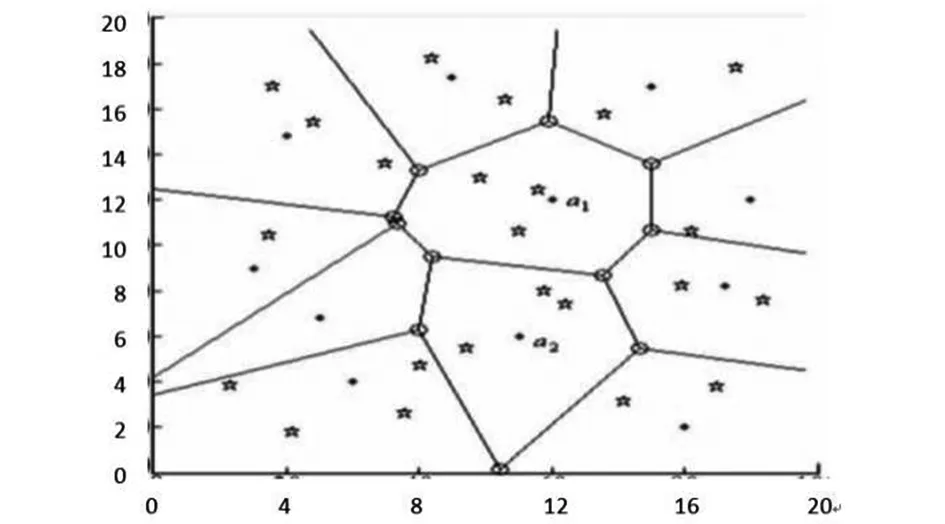
图3 定位空间Voronoi多边形图形构建Fig.3 Construction of Voronoi polygon in positioning space

2.2 实验结果

通过对定位区域内voronoi多边形进行构造，将其顶点位置设置成虚拟节点，这些虚拟节点中包含一个锚节点，与一些已知脆弱节点，经过信息交换等操作方式，获取虚拟节点的序列等级，进而得到voronoi多边形的定位结果.采用三种方法，展开以上步骤，研究其定位结果，在20 m×20 m的网络拓扑结构中，可得设计方法的实验结果如下表1所示.

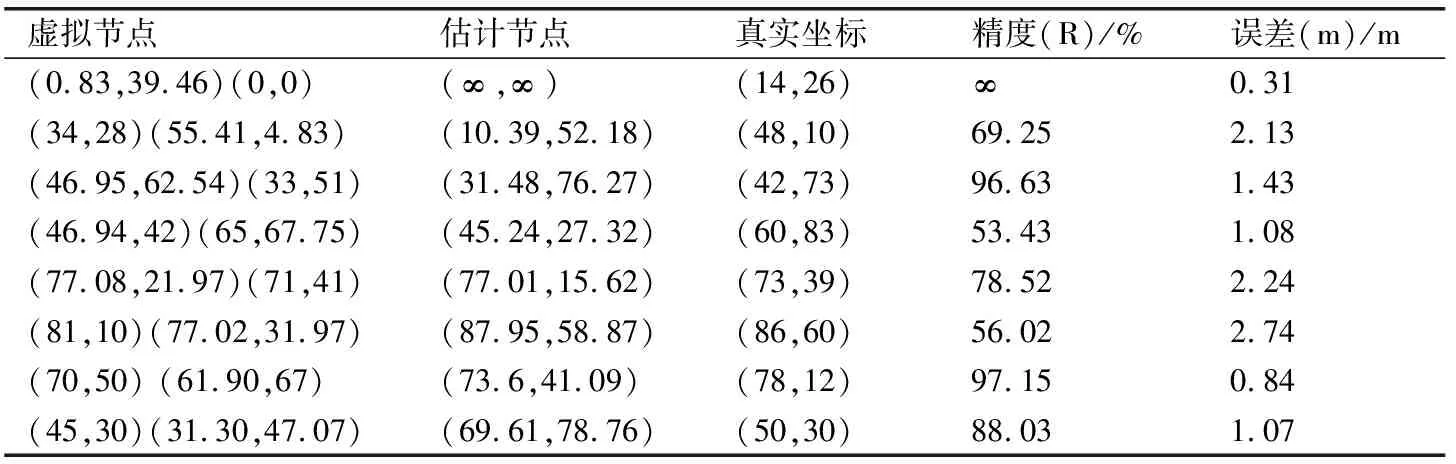
表1 设计方法节点误差分析Tab.1 Node error analysis of design method

两种传统方法的实验结果，分别如下表2与下表3所示.

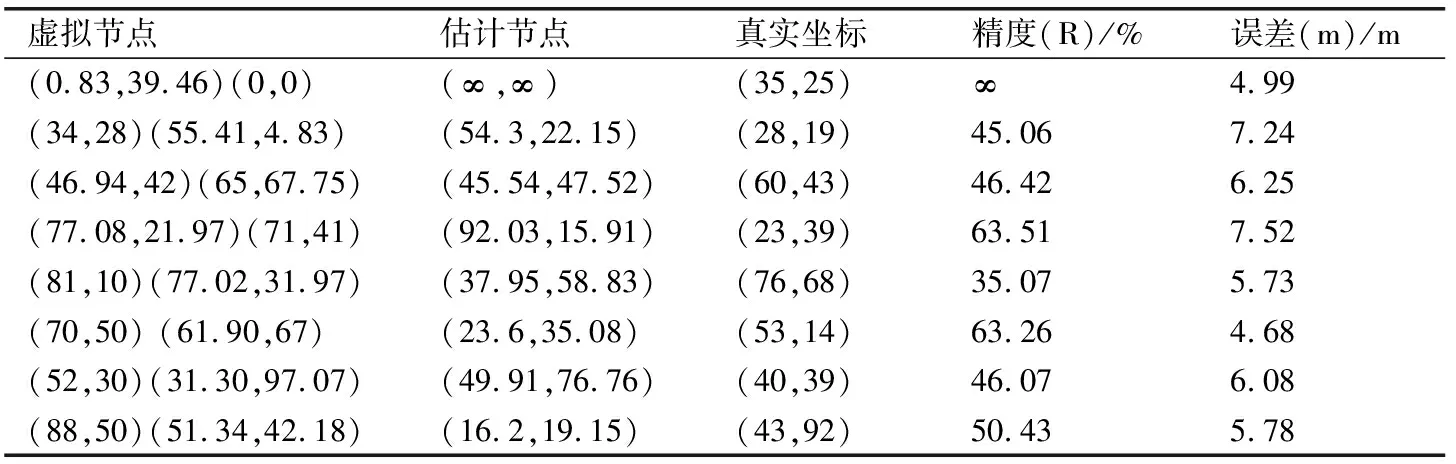
表2 传统方法一节点误差分析Tab.2 Node error analysis of Traditional method one

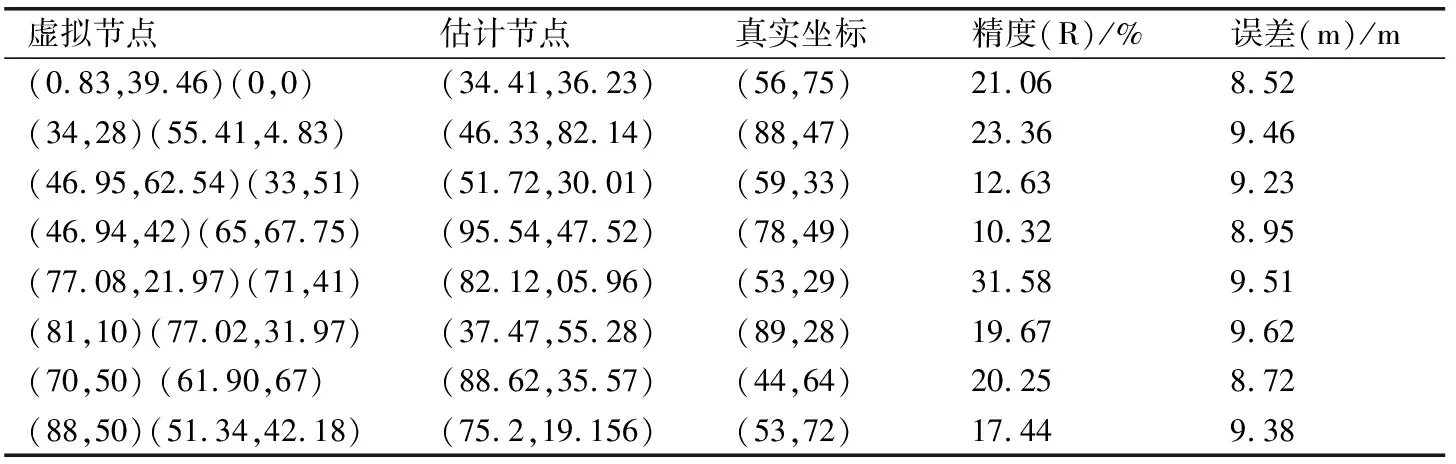
表3 传统方法二节点误差分析Tab.3 Node error analysis of Traditional method two

在计算机的网络定位空间中，构建voronoi多边形时，其中虚拟节点以随机分布的方式，广泛排列在定位空间[9-10].根据上表1、2、3可知，当虚拟节点相同时，定位方法的不同，会影响最终的定位效果，产生出不同的定位误差.从数据中可以发现，当虚拟节点为(0.83,39.46)(0,0)时，设计方法所产生的误差此时最小，为0.31 m；同样条件下，传统方法一所产生的误差为4.99 m，传统方法二所产生的误差为8.52 m.在三种方法的误差比较下，设计方法所产生的误差最小，较传统方法一小了4.68 m，较传统方法二小了8.31 m.

3 结束语

在计算机网络中，节点定位一般处于独立环境下运行，为用户提供网络服务.相较于传统方法，脆弱节点快速定位方法具有定位误差小的显著特点.通过无线网络传输的方式，在存在已知节点的情况下，对计算机应用层与网络层开展工作，进而实现节点的自我定位，因此，如何利用计算机网络，处理所得的节点信息，这对相关领域的发展十分重要.通过脆弱节点的快速定位，采集物理方面的节点信息，这种方法适用于很多场合，商业价值较大，这对未来节点的研究，有着巨大的价值和意义.