基于密度、功能指标的车站城市形态特征研究
2021-05-28陈恩山姜明池庄宇
陈恩山 姜明池 庄宇
同济大学建筑与城市规划学院
伴随着我国城市近三十年的扩张式发展,许多原本位于城市边缘的火车站逐渐进入到城市的中心,其独特的空间功能及形态衍生出空间更新以及紧凑发展的需求,站城融合成为备受关注的重点。自20世纪90年代以来,欧美等发达国家进行了很多火车站区域整体开发的实践,如荷兰、英国等借由火车站区域更新契机,打造新的城市中心,成功地带动了如国王十字车站区域、鹿特丹中央站区域的城市开发。城市在具体时段内,其自然环境、历史、政治、经济、社会、科技、文化等因素互动影响[1],城市更新设计涉及的要素众多、要素间的相互关系复杂,因此有必要选取适当的角度进行切中要害的分析。
城市形态作为城市的物质载体,体现了各类要素对城市的影响,其形态是设计师对各类城市要素进行设计操作最直接有效的平台。因此,针对城市形态的研究具有以点带面的作用。本文尝试提取形态的关键性指标,对车站区域的发展进行初步的形态现象解读。
1 概念界定:车站区域城市形态
1.1 车站区域
当下对国内火车站的研究多集中于宏观的交通格局和微观的火车站房设计,中/微观的、涵盖火车站和周边区域的研究较少。本文借鉴安德烈等人提出的火车站圈层理论[2],将车站步行合理区(Station Walkable)作为研究范围,即以火车站房为中心,选取普通人步行5min约400m为半径作圆,界定研究范围。
1.2 车站区域城市形态
城市形态有多样的解读角度,在建筑单体角度有美学构成等考量,在城市空间的感知有可意向性等评判。从国外的诸多经验可以看到,火车站区域的更新在很大程度上能带动区域的建设,因此对于开发潜力、容量的考察具有较高价值,故而本文选取空间使用强度作为形态的考察角度之一,采用密度相关指标进行形态考察分析。
1.3形态测度
在建筑学与城市规划学科中,围绕着密度的定义、测度、评价,诞生了很多指标及指标体系[3]。荷兰代尔夫特理工大学Meta Berghauser Pont教授将4种建筑密度指标结合在一起(建筑容积率FSI、覆盖率GSI、平均层数L和开放空间率OSR),建立了一种称之为“空间伴侣”(Spacemate)的图表[4],能有效地量化、区分不同城市形态与城市环境的密度状况(图1)。本文沿用其方法对车站地区的空间进行测度。
此外,除去开发强度,土地规划利用中土地的性质分布和功能配置也是规划与城市设计关注的重点。因此,对火车站这类以交通功能为主的区域,讨论其功能混合,具有较高的研究价值。由荷兰规划师范德赫克(Van den Hoek)提出的功能混合指标(MXI),能利用地块中居住、工作、设施这三种主要功能的建筑面积的比值,评价该地块的功能混合度高低,定量分析地块的功能特征[5](图2)。同时,MXI中居住与设施的比例,可以在一定程度上反应出场所—节点理论中火车站区域的场所和节点属性[6],因此采用MXI功能混合指标有助于与经典理论的对接和解读。
2 数据获取与处理
2.1 研究对象,案例库的选取
本次研究综合了车站流量、知名度等多项因素,在世界范围内选取了车站与站域周边附属开发关联度较高的38个案例。这些车站的客流量大多高于10万/天,为所在城市或区域最重要的车站。
2.2 密度数据获取
传统的密度指标多依赖官方搜集的数据,但因为国情的不同会导致很多地区数据缺失。本文统一从Cadmapper地图网站下载各车站站域的三维模型,通过Grasshopper软件进行指标提取,原理如下:
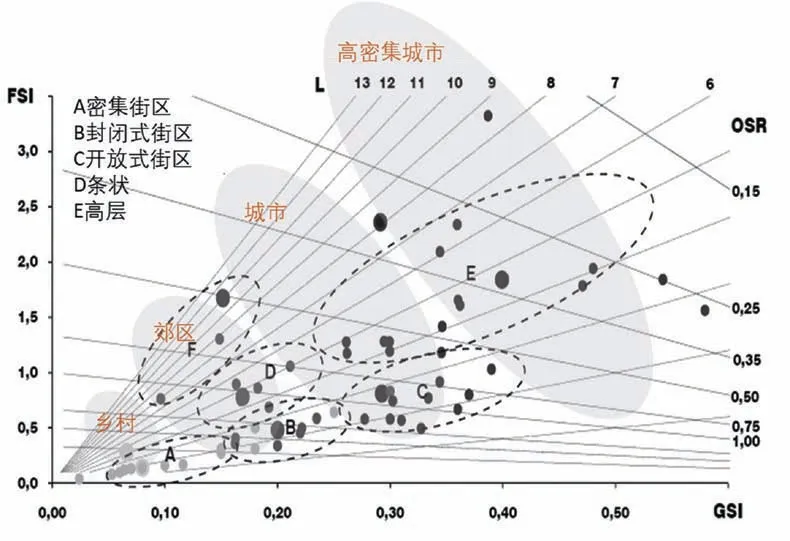
1 “空间伴侣”通过四类指标解释城市形态特征
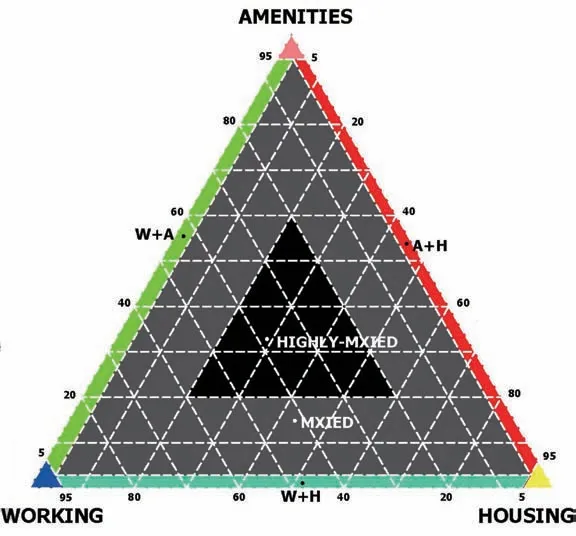
2 MXI图用功能比例描述混合度
(1)将城市模型导入Grasshopper,拾取各建筑轮廓面积求和,除以总基底面积,得到建筑覆盖率。原模型不含楼板,为获取容积率,通过Grasshopper软件中的等高线运算器,将建筑按层高切分楼层,拾取楼层面积叠加求和,再除以城市基底面积,求得容积率(图3,4)。
(2)结合资料查阅各国建筑层高,依据功能类型分析发现,办公及商业设施主体多为4m左右,住宅3m左右。本研究在暂不考虑功能细分的情况下,设定城市建筑的平均层高为3.5m。
(3)Spacemate所使用的开放空间率(OSR)、平均楼层数(N)两项指标,可以在覆盖率(GSI)和容积率(FSI)已经取得的情况下,由公式计算得出。平均楼层数=容积率/覆盖率,开放空间率=(1-覆盖率)/容积率。
2.3 功能数据的获取
人工识别Google Earth三维地图上各建筑的功能,将Cadmapper三维模型中的建筑按功能上色,采用与上述密度数据相同的获取方法,统计各类颜色所对应的建筑面积,获得各功能比例。
2.4数据处理与图解
在以覆盖率和容积率建立的直角坐标系中,平均楼层数对应的曲线为k=y/x,开放空间率为k=(1-x)/y。将密度数据导入空间伴侣图(图5),将功能比例数据导入三角图(Ternary Plot)获得功能混合度MXI图(图6)。
MXI图的功能混合度由三个值构成,数值本身无法直观反应混合度高低,只能借由最终的图像进行人工判断。为了将其转化为更易理解的、单一数值的比率指标。
本文进一步提出“综合功能混合度M1”:设MXI图中心点到某散点的距离为a,中心点到端点的距离为b(图7,8),综合功能混合度M=1-a/b。该值介于0~1之间,数值越大则功能越混合。对应于MXI图,当散点位于中心点时,功能混合度最高,M=1;当散点位于端点时,功能混合度最低,M=0。依此原理计算计算各车站功能混合度值(表1)。
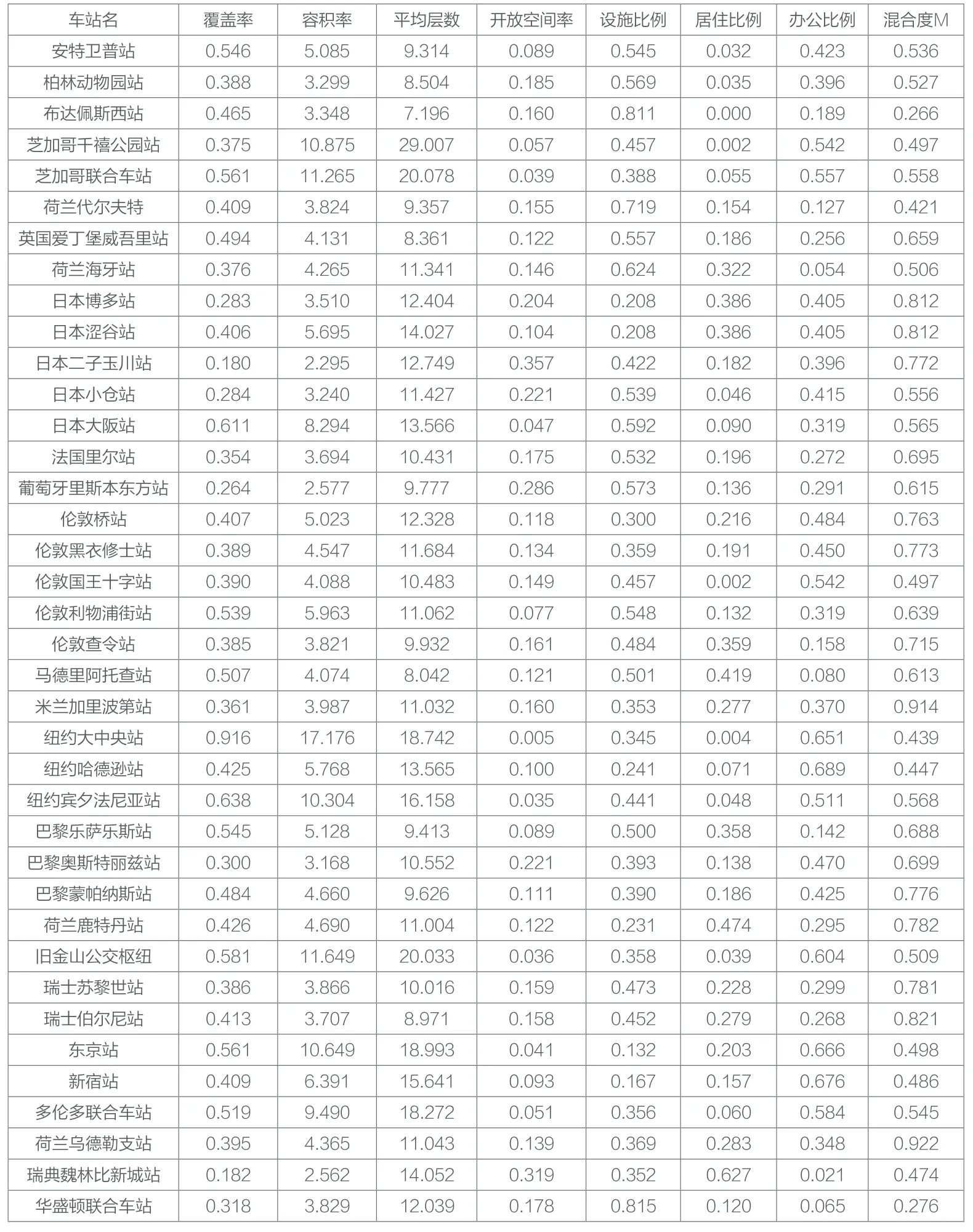
表1 密度与功能数据

3 Cadmapper下载的原始模型
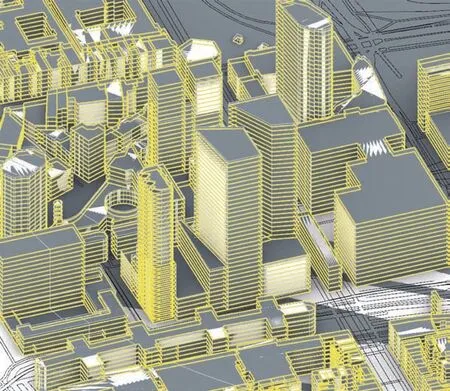
4 Grasshopper编程生成楼板线
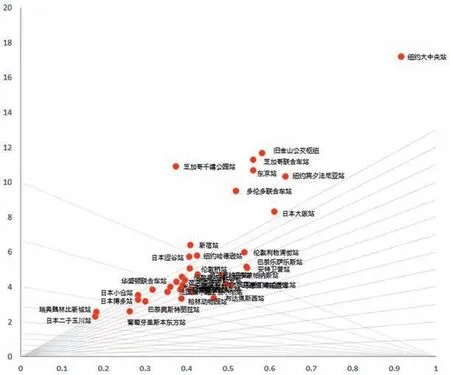
5 车站区域数据绘制的“空间伴侣”图
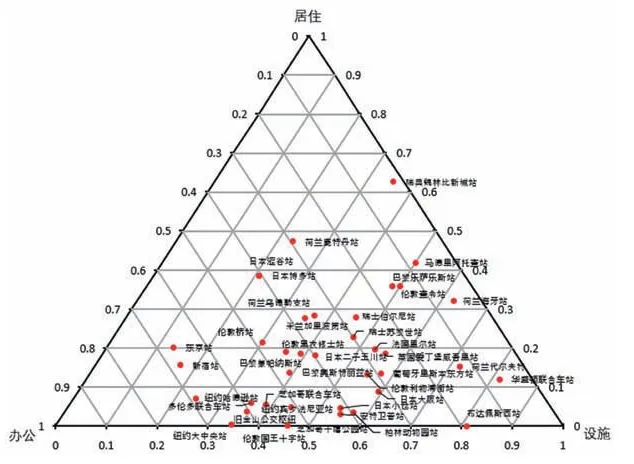
6 车站区域数据绘制的MXI图
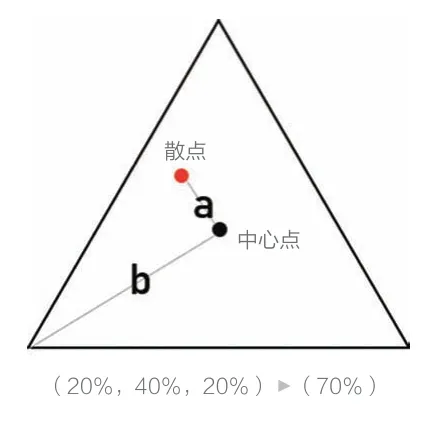
7 “综合功能混合度M”定义-平面图解

8 “综合功能混合度M”定义-三维图解

表2 各指标相关性分析
为了进一步观察密度与功能各指标间是否存在关联,用SPSS软件对指标进行相关性分析2(表2)。
3 形态与功能特征
3.1 密度分布特征
由空间伴侣图可见:
(1)车站总体覆盖率为0.18~0.92,最大值与最小值比值为5.1;容积率为2.3~17.2,最大值与最小值比值为7.5;建筑平均层数8.0~29.0层;开放空间率均小于0.35。
(2)密度分布有很强的区域差异。美洲的车站覆盖率、容积率、平均层数均最高;人们印象中很拥挤的日本,站区密度指标在各个水平上均有分布;重视传统保护的欧洲,覆盖率、容积率处于中低水平,平均层数较低。
(3)具体案例中,作为全球客流量最大的车站,新宿站的各类密度指标均处于中间水平;纽约大中央站覆盖率达到0.92,容积率为17.2,密度指标最高(图9,10)。
3.2 功能分布特征
由功能混合MXI图可见:
(1)车站区域建筑功能多偏向于工作和设施,居住功能比例相对较低。一方面火车站域的噪音等问题难以处理对居住影响较大;另一方面办公与商业等建筑类型对火车通勤以及通勤人流的需求更高。多因素综合下使目前车站总体开发中,增加商业、办公功能对开发商来说更有利可图。
(2)美国案例含有高比例办公功能,与美国火车多用于短途办公通勤的现象吻合。欧洲以荷兰等国为代表,功能混合度较高,车站作为交通节点和城市生活的场所均得到较强体现(图11,12)。
3.3 密度与功能间的关联特征
由表2可见:
(1)所有密度指标与综合功能混合度M进行相关性运算,所得相关系数均较低,说明了密度的高低和功能混合程度的高低不存在关联。但单独的办公功能与覆盖率、容积率、平均楼层数等密度指标均有很强的正相关性,反应了目前世界范围内,高密度火车站地区存在高比例办公现象。
(2)密度指标内部相互进行相关性运算,覆盖率和容积率之间的相关系数为0.799,两要素强相关,说明在高密度地区,同时增大覆盖率和容积率是常见的城市形态设计策略。开放空间率与容积率、覆盖率的相关系数分别为-0.860和-0.787,说明容积率的提升对开放空间率负面影响更大。
(3)混合度指标内部相互进行运算,设施比例和混合度之间的相关系数为-0.428,其背后的原因可能是早期建成的车站周边以货运仓储为主、功能混合度低,而伴随着更新,车站区域货运仓储搬迁,引入办公住宅等功能,走向均衡发展。住宅和混合度的相关系数为0.483,呈现正相关性,可能出于同样原因。
4 形态策略
目前中国很多车站区域容积率仅有2.0~3.0,而世界范围内,部分国家如美国其车站地区容积率高达10.0以上。因此国内可以在更详细论证的基础上,借鉴紧缩城市、TOD等理论,大幅增加建筑的容量以提高土地利用效率。国内少量新近项目,如重庆沙坪坝火车站、上海万科之城,初步实现了车站区域的高密度建设,可以为未来新建项目提供借鉴。
车站更新与形态在0.4~0.6覆盖率区间,容积率的变动范围达到了3~12,有4倍之差。可以猜想,在路网格局不变的情况下,覆盖率在0.4~0.6的车站地区,可以通过增加建筑层数的形态设计策略加大建筑容量。在车站更新的大趋势中,这类车站区域也有望成为极具潜力、易于操作的更新站点。
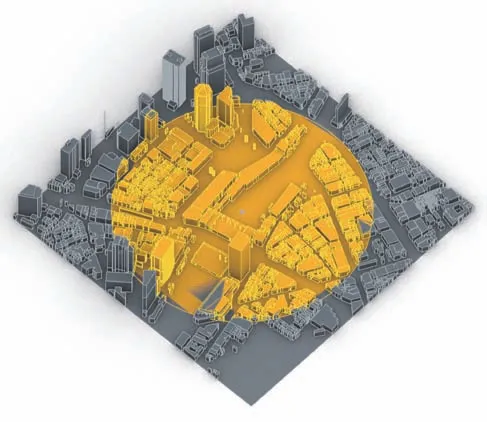
9 东京新宿站车站区域空间形态

10 纽约大中央站车站区域空间形态
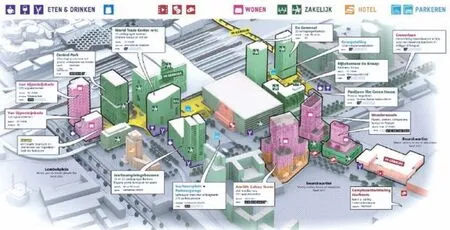
11 荷兰乌德勒支车站西侧区域功能分布
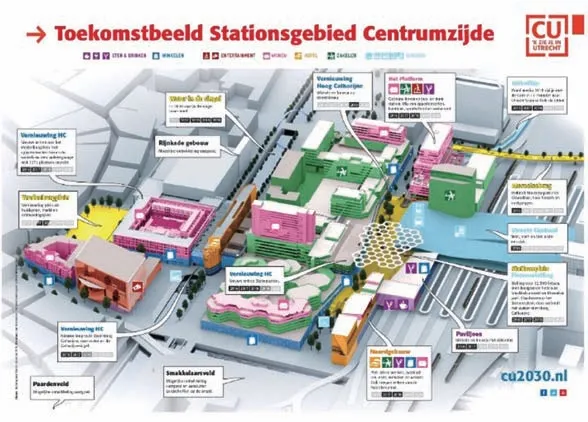
12 荷兰乌德勒支车站西侧区域功能分布
5 讨论与展望
本研究提取数据的方法,尤其是密度数据的提取,无需进行手工建模测算,从而可以克服传统的依托主观感受评价大样本的局限。在对数据的图解分析中,提出综合功能混合度指标M,完善了原MXI混合度指标体系,使结果变得更加直观,并且为混合度数据与其他单指标数据提供了整合分析的基础。然而,本文的研究结论也存在一定的缺陷,尽管通过量化研究的方式探讨了各个指标之间开发强度的相关性,然而其背后的发展原因和分布规律还有待进一步探索,以期为我国站城空间规划设计提供更具参考意义的实践依据。
图表来源
图1由文献[4]改绘;图2来源于文献[5];图11,12来源于CU2030官网;其余图表均为作者自绘。
注释
2 通常情况,两组变量的Pearson相关系数R的取值,在0.4~0.6为中等程度相关,0.6~0.8为强相关。需要注意的是,相关系数的高低只表明两变量间是否存在概率上的关联,并不代表必然的因果关系。
