基于BP神经网络对复杂机电系统可靠性的评估
2021-05-28阚延鹏刘永明
阚延鹏,陈 玉,刘永明,韩 波
(安徽工程大学 机械工程学院,安徽 芜湖 241000)
如今,工业机器人的发展程度是衡量各个国家制造业水平的一个标准,因此,工业机器人的可靠性研究尤为重要,准确地评估能有效地降低系统故障率。掌握机器在不同工作时间下的可靠度能及时对部件进行维护,提高使用寿命。研究的六自由度工业机器人由控制柜和机械本体组成,包括机械件、电子元器件等部件。整个系统可靠性水平的高低主要取决于关键部件,因此需要对关键部件进行可靠度计算。近年来,国内外对可靠性的预测做了很多研究。李翠建立故障树可靠性模型对数控机床可靠性进行分析。Chen Luyi等采用遗传算法来选择RBF神经网络的径向基函数中心和径向基函数宽度,并对隐含层和输出层进行线性加权来对机器人可靠性进行预测。田震等采用粒子群算法优化BP神经网络预测可靠性,把影响因素作为模型输入,采煤机可靠度为目标输出值。沈国强等利用图解法和改进的ABC算法对三参数威布尔模型的参数进行估计和优化,并用该模型计算机车关键零部件的可靠度指标。常彪建立威布尔分布的数学模型,以关键部件的故障为依据计算可靠性。杨培林等利用概率行为树建立了机电系统的形式化模型后用概率模型检测评价可靠性。胡杰利用数学公式对高速包装机器人的子系统进行可靠度计算,并建立故障树对机器人进行可靠性分析。对于可靠性预测,现有的方法是利用影响因素和故障数据来预测其可靠性、建立数学模型,利用数学公式建立故障树等来分析可靠性,而对于复杂的机电系统,用这些方法过于复杂并且不能准确的评估。
研究是采用BP神经网络算法来预测复杂机电系统的可靠性,模型中电子元器件数据根据GJB/Z 299C-2006《电子设备可靠性预计手册》得出,非电子元器件原始数据根据NPRD-2016非电子元件可靠性数据库得出,用威布尔分布函数和指数分布函数分别算出机电系统中的非电子元器件和电子元器件在不同工作时间下的可靠度。根据可靠度值,利用BP神经网络建立可靠性预测模型,预测机电系统整体的可靠度,完成结果分析。
1 150 kg六自由度工业机器人系统及BP神经网络模型
1.1 150 kg六自由度工业机器人系统

图1 150 kg六自由度工业机器人 图2 控制柜
150 kg六自由度工业机器人如图1所示。装有组成机器人的电子元器件的控制柜如图2所示。组成机器人机电系统的手腕、底座、防爆小电柜的各部名称及个数如表1所示。

表1 组成部件

物料描述数量熔芯2熔断器2接线端子129接线端子22机器人线束11机器人线束21机器人线束31机器人线束41机器人线束51指示灯11指示灯21指示灯31按钮1选择开关1减压阀1电磁阀1压力开关2
1.2 BP神经网络可靠性评估模型
BP神经网络是以误差反向传播算法训练的多层神经网络。模型结构包括输入层、输出层、隐含层,研究采用的是三层神经网络,使用梯度下降法反复训练,调整各层神经元的权值和阈值。当网络的实际输出值与期望值的误差均方值为最小时,即可得到最终结果。BP神经网络结构如图3所示。由图3可见,输入层神经元节点数是R
到R
;输出层神经元节点数是O
;隐含层神经元节点数是K
到K
;输入层到隐含层的权重为w
;隐含层到输出层的权重为w
;输入层到隐含层的偏置是b
到b
;隐含层到输出层的偏置是v
到v
;学习速率为δ
;激活函数f(x)
采用Sigmoid函数17,是非线性连续函数,常用于解决复杂问题,取值范围为(
0,
1)
,Sigmoid函数的图像如图4所示。可表示为:
(1)

图3 三层神经网络结构图 图4 Sigmoid函数图像
BP神经网络可靠性评估模型的隐含层输出可表示为:

(2)
输出层的输出可以表示为:
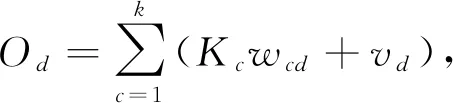
(3)
期望值与实际输出值之差可以表示为:
e
=R
-R
,
(4)
误差计算采用均方误差算法,均方误差的值越小表示模型的预测结果越精确,计算公式可以表示为:
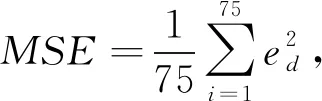
(5)
权值更新公式可以表示为:

(6)
w
=w
+δK
e
,
(7)
阈值更新公式可以表示为:

(8)
v
=v
+δe
,
(9)
式(2)到式(9)中:a=
1,
…,
35;c=
1,
…,k;d=
1;i=
1,
…,
75。2 数值仿真
2.1 模型数据
机械件的失效率根据其型号和工作环境类别参考NPRD-91,电子元器件的失效率参考GJB/Z 299C,机械件和电子元器件的寿命分别服从威布尔分布和指数分布,所有部件的工作时间设置为100 h到15 000 h,模型数据如表2所示。
2.2 仿真结果
采用BP神经网络评估机电系统的可靠性的核心思想是把组成机电系统的各件在不同时间下的可靠度作为模型的输入,将由公式计算得出的不同时间下整体的可靠度作为输出,训练网络。网络设置最大的迭代次数5 000次,学习速率是0.3,训练目标最小误差是10,采用随机划分的方法划分数据集,计算误差采用均方误差算法。隐含层神经元节点个数根据式(10)计算。

(
10)
式中,m
为输入神经元节点数量;n
为输出神经元节点数量;a
的取值范围为[
1,10]
。由式(10)计算可知隐含层神经元节点个数的取值范围为[7,16],在此范围内,取不同的隐含层神经元个数,比较网络训练的最终结果,如表3所示。由表3的训练结果对比可知,隐含层神经元个数在[7,16]范围内网络训练的最终误差都小于目标误差,在隐含层神经元个数取10时,迭代次数最小且阻尼因子大,说明收敛效果最好,故隐含层神经元取10个。
利用建立的预测模型对样本数据进行训练,综合考虑误差、迭代次数、阻尼因子等,当运行效果最好时,记录下数据,研究中网络训练实际迭代次数是2次,收敛率高,最大误差是0.005 66,最终得到的均方误差是8.72×10,小于目标差,训练效果较好,训练中均方误差的变化如图5所示。
该网络模型采用的是梯度下降的方法,泛化能力较好,由训练结果可知最大梯度为0.031 1,阈值梯度为10,实际梯度为0.000 171,阻尼因子训练实际值是,收敛效果较好;在训练过程中需要用验证数据检验每次的输出误差,由训练结果可知验证检查为0,表示误差在持续降低,训练状况如图6所示。

表2 机电系统中各件的失效率和在不同工作时间下的可靠度

表3 可靠性预测模型在不同隐含层神经元个数下的网络训练结果比较

图5 误差图 图6 训练状况
复杂机电系统可靠度预测结果对比如图7所示。由图7可以看出,真实值与预测值能较好地拟合,模型决定系数是0.999 44,表明BP神经网络能较好地实现机电系统可靠性的预测,模型的性能较好。从数值上看,系统的可靠性随着工作时间的增多而降低,在10 700 h内可靠度都在0.9以上,工作时间到达12 500 h后要更加注意系统的工作状态,及时进行维修或更换部件。将预测值与真实值对比,如表4所示。

图7 BP神经网络预测对比图

表4 预测值与真实值的对比
由BP神经网络预测的可靠度值与真实值对比可得,预测值与真实值之间的误差很小,说明通过BP神经网络预测模型训练效果较好,用个体可靠度能较为准确地预测系统整体可靠度。研究的150 kg六自由度工业机器人的预测可靠性如表5所示。

表5 150 kg六自由度工业机器人的可靠性

工作时间/h整体可靠度120000.891629289140000.866886871
3 结论
基于BP神经网络建立了工业机器人复杂机电系统的可靠度预测模型,以各个部件在不同时间下的可靠度作为模型的输入,整个系统在不同时间下的可靠度作为模型的输出。组成部件中电子元器件和机械件的寿命分别服从指数分布、威布尔分布,以此为依据计算可靠度,仿真结果验证了模型的准确性、可行性。通过BP神经网络实现了个体预测整体,提高了可靠性评估的精度,相比传统的可靠性评估方法,该方法更简便、使用范围广,在可靠性评估方面有重要的意义。采用BP神经网络建立工业机器人的可靠度预测模型,从模型输出结果可知,150 kg六自由度工业机器人的机电系统在时间5 000 h、7 000 h、11 000 h的可靠度分别是0.951 170 709、0.933 098 447、0.898 372 665。
