地铁轨道参数及周围环境对埋地管道保护电位影响的ANSYS分析

田逸凡 李建三 易宏 刘振斌

摘 要：为了探究地铁杂散电流对埋地管线的影响规律，应用ANSYS有限元分析软件，对多种情况下埋地管道受地铁走行轨的影响进行仿真分析，并选取金属管线外表面的节点电压值生成沿管道长度的电场强度分布图以及管道保护电位分布图，讨论不同轨道参数及周围环境条件下地铁杂散电流对管道的影响规律。研究结果表明：随着管道与走行轨交角的增大，管道周围土壤电场强度整体减弱;走行轨与管道交叉角度的大小会影响埋地管道电位最高值出现的位置;土壤介质、轨道与管道间距以及地铁轨道工况电压均会影响管道保护电位的大小;走行轨正极区域对管道保护电位的影响程度远大于其负极区域。所建模型合理可行，研究结果对于日常燃气管道电位监测具有参考价值。

关键词：石油、天然气能;走行轨;埋地管线;电场强度;管道电位

中图分类号：TE88   文献标识码：A

DOI： 10.7535/hbgykj.2021yx02001

ANSYS analysis of the influence of subway track parameters and

surrounding environment on the buried pipeline protection potential

TIAN Yifan1， LI Jiansan1， YI Hong2， LIU Zhenbin1

（1.School of Mechanical & Automotive Engineering， South China University of Technology， Guangzhou， Guangdong 510640，China;2. Guangzhou Gas Group Company Limited， Guangzhou， Guangdong 510635， China）

Abstract：In order to explore the influence law of subway stray current on buried pipelines， the finite element analysis software ANSYS was used to simulate the impact of subway running rail on buried pipelines under various circumstances. The node voltage values on the outer surface of the metal pipelines were selected to generate the electric field intensity distribution map along the pipeline length and the pipeline protection potential distribution map. The influence law of subway stray current on pipeline under different track parameters and ambient conditions was discussed. The results show that with the increase of the crossing angle between the pipeline and the running rail， the soil electric field intensity around the pipeline weakens; the crossing angle between the running rail and the pipeline can affect the position of the highest potential value of the buried pipeline; the soil medium， the distance between the track and the pipeline， and the operating voltage of subway track can affect the protective potential of pipeline;the effect of the positive pole on the protection potential of the pipeline is greater than that of the negative pole. The research model is reasonable and feasible， and the research results have certain reference value for daily potential monitoring of gas pipelines.

Keywords：oil and natural gas energy;running rail;buried pipeline;electric field intensity;pipeline potential

近年來，为了缓解城市交通压力，很多城市都投入大量资金修建地铁，截至2019-06-06，中国开通地铁的城市已有33个，随着地铁系统规模的增大，地铁线路不可避免地与燃气管道线路出现位置的交叉或并行，地铁运行中产生的杂散电流给燃气管线所带来的危害也日益增大[1-3]，因此，开展埋地管线杂散电流腐蚀研究具有重要的理论及实际意义。朱祥剑等[4]对地铁杂散电流干扰下的埋地管线通、断电位进行监测并将数据进行系统分析，总结了管道电位波动规律。但实际现场环境复杂、影响因素众多，真实电位数据获取难度大，所得规律也具有局限性。李伟等[5]通过室内模拟试验研究了直流杂散电流干扰规律，但试验为了模拟真实土壤而采用自来水配制土壤模拟液，试验条件很难达到与实际情况完全一致。因此开展模拟研究成为比较有效的研究方法，李琴等[6]建立双边供电直流电车杂散电流对管道电位干扰模型，采用MATLAB进行数值模拟，但这种电路模型只能求解管轨平行状态时的分布规律，且模型较为理想。程浩[7]建立列车有限元模型，模拟杂散电流作用下埋地管道的电流、电位分布，但对于不同条件下受杂散电流影响的管线阴极保护电位分布缺乏深入研究。

本文运用ANSYS有限元分析软件[8]，在不同地铁轨道与管道的交叉角度、间距、土壤介质以及地铁运行工况等因素条件下，进行模拟分析，生成土壤电位分布云图，并绘制沿管道长度的保护电位曲线，根据电位曲线分析得到杂散电流对管道保护电位的影响规律。

1 有限元模型

在工程分析领域中，有限元法是应用非常广泛的一种数值计算方法。因具有操作简单、应用性强、结果可靠等优点，ANSYS在结构、热、声、流体以及电磁场等学科领域的研究中被广泛应用。本文建立地铁轨道-埋地管线-土壤环境的杂散电流分布模型，并在ANSYS电磁场模块中进行有限元分析。

为了全面研究交叉情况下地铁杂散电流分布情况，分别设置地铁轨道与埋地管线交叉角度为0°，30°，45°，60°和90°。在土壤表面埋设走行轨，在距地表10 m处埋设金属管线。走行轨采用实心圆柱模拟，走行轨下方半圆柱模拟浇筑的钢筋混凝土区域，模型土壤区域采用200 m×50 m×200 m的立方体模拟。建模时将地铁走行轨中心点作为有限元模型坐标系的原点，ANSYS模型如图1所示。

为了能更真实地模拟地铁杂散电流对金属管线管道电位的影响，有限元模型中的材料规格及属性均是根据实际情况以及相关标准进行定义的。图1中走行轨直径为300 mm，绝缘层厚度为3 mm，金属管道规格为D508 mm×7.9 mm，管道保护层厚度为3.2 mm，两者长度均为200 m。模型的计算参数如表1所示[9-10]。

在模型中，土壤采用软件内置的自由四面体进行网格划分，由于轨道直径、管道直径和混凝土部分尺寸相对于土壤来说较小，故采用自定义尺寸进行网格划分。轨道、管道和混凝土部分网格划分最大单元尺寸为200 mm，最小单元尺寸为40 mm。所建模型总共包含1 508 162个节点，808 692个单元。网格模型见图2。

2 ANSYS仿真分析

现实生活中地铁杂散电流是动态变化的脉冲电流，但由于电场传播速度几乎等同于光速，故可将地铁杂散电流概化为瞬时恒定流[11]。文中的有限元模拟中，只考虑第一类边界条件，模拟土壤的立方体下底面为大地无限远处，大地无限遠处施加0 V的约束电压[12]。在未受外界干扰的情况下，埋地金属管道阴极保护电位应为-0.85～-1.2 V（CSE）[13]，故可以在金属管道两端各施加一个-1.2 V的电压来模拟管道保护电压[14-15]，土壤表面的走行轨前后两端分别施加35 V和-35 V的干扰电压[15]。

由于管道两端保护电压远小于轨道两端电压，所以轨道电压是影响周围土壤电位的主要因素，交叉情况下轨道周围土壤电位分布云图如图3—图4所示。

从图3与图4中可以看出，当走行轨未施加电压时，土壤电位受埋地管线保护电压影响，土壤电位沿管线对称分布;当地铁正常运行时，走行轨左右两端施加电压时，走行轨正极施加35 V电压导致周围土壤电位增大，走行轨负极施加-35 V电压使得周围土壤电位减小，因此地铁正常运行时势必也会对土壤中埋地管线保护电位产生影响。

2.1 地铁杂散电流对埋地管道电位影响规律验证

地铁运行过程中，由于走行轨对地绝缘不充分，回流电流会从走行轨泄漏到土壤以及埋地金属中。通常可以将走行轨、大地以及埋地金属各自电位高低幅度作为衡量指标来分析杂散电流的方向、大小和区域等综合情况[16]。地铁工作中，大地电位会受到走行轨电位的影响，而大地电位的变化也必将会导致埋地金属电位的变化[17]，这在仿真得到的土壤电位分布云图中可以清楚地看到。

若以无限远大地为基准，地铁所在位置附近为走行轨电压正极区，在变电所整流器位置附近为走行轨电压负极区，走行轨、埋地管线的电位分布[16]如图5所示。

当管道未施加保护电压时，通过仿真读取沿走行轨、埋地管道以及埋地管道附近土壤节点电压，生成电位分布图（见图6）。由图6可见，走行轨左右两端为35 V和-35 V干扰电压，距走行轨10 m处的管道电位以及附近的土壤电位都发生偏移，由于埋地管道保护层的保护作用，电位偏移值最小，管道电位最大偏移幅度达到5.1 V。对比图5和图6，可以看出仿真结果与理论规律相符合，在走行轨正极区，埋地管道周围土壤电位大于埋地管道电位;在走行轨负极区，埋地管道周围土壤电位小于埋地管道电位。若以管道对附近大地的电位差（对地电压）来进行说明，在走行轨正极区域埋地管道对地电压小于0，杂散电流流入金属管道，而走行轨负极区域埋地管道对地电压大于0，杂散电流从金属管道流出，这与实际情况也是相符的。综上所述，本文仿真结果是合理可靠的。

2.2 走行轨电压对管道附近土壤的影响分析

为了进一步研究走行轨电压对管道周围土壤的影响，以管道接触土壤为研究对象，沿管道方向，绘制当走行轨两端施加干扰电压并且埋地管道施加保护电压时，轨道与管道交叉角度在0°～90°临近土壤的电场分布曲线，如图7所示。

从图7中可以看出，走行轨两端施加电压时，受交叉角度影响，管道周围土壤电场强度由0°的近似对称状态转变为非对称状态，最后再到90°时的对称状态。由不同交叉角度结果对比可知，随着管道与走行轨交叉角度的增大，管道周围土壤电场强度整体减弱。靠近走行轨正极区的土壤电场强度大于靠近负极区土壤电场强度，说明走行轨正极区对管道周围土壤干涉效果要大于负极区。

2.3 交叉角度对管道电位的影响分析

在有限元模型及其计算参数不变的情况下，改变轨道与管道的交叉角度，设置交叉角分别为0°，30°，45°，60°和90°，来研究交叉角度的变化对管道保护电位的影响。读取金属管线外表面的节点电压值，绘制沿管道走向的保护电位分布图，如图8所示。

由图8可见，随着交叉角度的增大，埋地管道保护电位所受影响减小;当埋地金属管道与走行轨交叉角度为0°时，管道保护电位所受干扰程度最大，管道电位正向可达到+1 720 mV，相比较原始保护电位偏移了+2 920 mV，管道电位负向可达到-2 688 mV，相对于原始保护电位偏移了-1 488 mV。除了交叉角度0°以外，其他交叉角度下管线电位值绝大部分在-1.2 V以上，由此可见，受影响的管道阴极保护电位多为正向偏移。

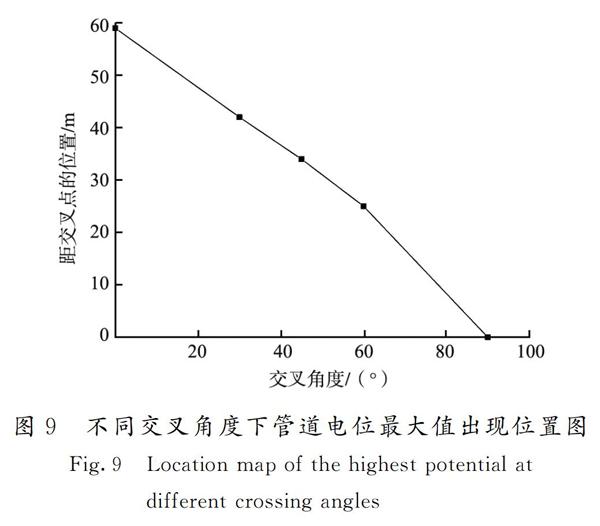
图9所示为不同交叉角度与管道电位最大值的位置关系，可以看出，随着交叉角度的增大，管道电位最大值所处位置从走行轨正极区向交叉点位置偏移，交叉角度为0°时电位最大值在管线41 m处，30°时在58 m处，45°时在66 m处，60°时在75 m处，90°时在100 m处。因此，在地铁周围铺设金属管道时，尽可能增大交叉角度来减小地铁杂散电流对管道电位的影响，日常检查工作要重点监控管道正向偏移最高点位置的管道电位。

2.4 土壤介质和轨道参数对管道电位的影响分析

2.4.1 不同土壤介质下管道电位影响分析

在有限元模型及其计算参数不变的情况下，通过改变土壤介质研究管道在不同土壤中受地铁杂散电流的影响规律，不同土壤介质的计算参数[18-19]见表2。

由于不同的交叉角度对应的管道电位随土壤介质的变化规律趋势相同，故以交叉角度30°为例，读取金属管线外表面的节点电压值，绘制沿管道走向的保护电位分布图，如图10所示。

从图10中可以看出，不同的土壤介质下管道电位受干扰情况不同，土壤相对介电常数越大，地铁运行对周围环境的电场强度影响也越大。当处于走行轨正极区时，各土壤介质下管道电位均发生明显的正向偏移。土壤介质杂散电流传导能力越强，管道电位偏移程度也会越大，不同土壤介质下的管道电位最大值出现位置不变，但电位值由介质1时的-0.11 V上升到介质4时的0.49 V。

2.4.2 不同间距下管道电位影响分析

在有限元模型及其计算参数不变的情况下，设置不同的管道埋深，从而改变管道与走行轨之间的距离，研究不同间距下管道保护电位受杂散电流的影响规律。以交叉角度30°为例，读取金属管线外表面的节点电压值，绘制沿管道走向的保护电位分布图，如图11所示。

从图11中可以看出，随着走行轨与管道间距的减小，管道电位波动值出现增大趋势。以交叉点位置为分界点，走行轨正极区域内两者间距越小，管道电位正向偏移越大;走行轨负极区域内两者间距越小，管道电位负向偏移越大。當走行轨与管道间距增大到40 m时，管线电位依然受地铁影响，管道电位可达-10 mV，相对于原始保护电位偏移了+1 190 mV。因此，即使在此间距下杂散电流对埋地管道的影响依然不能忽视。

2.4.3 不同工况电压下管道电位影响分析

在有限元模型及其计算参数不变的情况下，设置不同地铁工况参数，研究不同工况下地铁杂散电流对管道电位的影响，具体运行工况[15]见表3。现以交叉角度30°为例。读取金属管线外表面的节点电压值，绘制沿管道走向的保护电位分布图，如图12所示。

从图12中可以看出，走行轨两端施加的电压越大，埋地管道所受影响也越大。管道电位最高点出现的位置没有发生变化，均在管道58 m处。4种工况下的管道电位最大值分别为0.08，0.17，0.28，0.38 V，可以看出电位最大值以约0.1 V的大小增长。并且，管道电位均大于或者等于原始保护电位，轨道正极区域对管道电位影响程度远大于负极区域。因此，在日常的杂散电流防护工作中要重点加强对正极区段管道的防护。

3 结 语

本文建立的地铁轨道-埋地管线-土壤环境杂散电流分布模型，通过改变管轨交叉角度、管轨间距、土壤介质和轨道载荷等因素来研究地铁杂散电流对埋地管道阴极保护电位的影响。根据研究所得结果，可以得出以下结论。

1）随着管道与走行轨交叉角度的增大，管道周围土壤电场强度整体减弱。电场强度分布经历了由对称到非对称再到对称的规律变化，并且均在轨道与管道交叉点位置达到最小值。

2）管道保护电位所受杂散电流的干扰会随走行轨与埋地管线交叉角度的增大而减小。不同的交叉角度管道电位最高值出现的位置也不同，交叉角度在0°～90°时，随着角度的增大，最高值的位置向交叉点方向偏移。除此之外，土壤介质、走行轨与管道间距以及轨道工况电压都会对管道保护电位造成影响，但对管道电位最大值的位置并无影响。

3）轨道正极区对管道周围环境干涉效果最大。轨道正极区对周围土壤电场和管道电位影响程度大于负极区域，在地铁周围铺设金属管道时，应尽可能远离轨道正极区来减小轨道电位的影响。

文中建立的模型大小为200 m×50 m×200 m，虽然相比于常见的缩小简化模型更符合实际情况，但是对于现实中近千米长的轨道和管道而言，模型依然较小，需要增加模型尺寸，根据现场情况不断调整，提高模型准确度。接下来的工作，将尝试模拟千米长管道上存在保护层小破损面积时的管道电位变化曲线。

参考文献/References：

[1] 周军峰，谭海川，张鑫，等. 直流杂散电流对天然气管道干扰影响案例分析[J]. 腐蚀与防护，2018，39（9）：713-718.

ZHOU Junfeng， TAN Haichuan， ZHANG Xin， et al. Case study on influence effect of DC stray currents on natural gas pipelines[J]. Corrosion & Protection， 2018，39（9）：713-718.

[2] 杨理践，黄平，高松巍.有效抑制电气化铁路对油气管道管地电位影响的技术[J]. 材料保护，2015，48（6）：48-51.

YANG Lijian， HUANG Ping， GAO Songwei. Technology to efficiently suppress the impart of electrified railway on pipe-to-soil potential of oil and gas pipeline[J]. Materials Protection，2015，48（6）：48-51.

[3] 劉瑶，谭松玲，邢琳琳，等.北京埋地燃气管道地铁杂散电流干扰影响现场检测及规律分析[J].腐蚀科学与防护技术，2019，31（4）：429-435.

LIU Yao， TAN Songling， XING Linlin， et al. Detection and analysis of interference with buried gas pipelines from subway stray current in Beijing area [J].Corrosion Science and Protection Technology， 2019，31（4）：429-435.

[4] 朱祥剑，杜艳霞，覃慧敏，等. 地铁杂散电流干扰下埋地管道管地电位动态波动规律[J]. 腐蚀与防护，2019，40（12）：878-885.

ZHU Xiangjian， DU Yanxia， QIN Huimin， et al. Dynamic fluctuation characteristics of pipe-to-soil potential on buried pipelines under interference of stray current from subway[J]. Corrosion & Protection， 2019，40（12）：878-885.

[5] 李伟，杜艳霞，王洁军. 直流杂散电流干扰缓解方法及其适用性[J]. 工程科学学报，2016，38（7）：958-966.

LI Wei， DU Yanxia， WANG Jiejun. Mitigation methods and their applicability for DC stray current interference[J]. Chinese Journal of Engineering， 2016，38（7）：958-966.

[6] 李琴，陈奔，黄志强，等. 直流电车杂散电流对城市燃气管道电腐蚀的影响规律研究[J]. 材料保护，2019，52（4）：66-72.

LI Qin， CHEN Ben， HUANG Zhiqiang， et al. Influence of stray current in direct current railway system on electric corrosion of pipelines[J]. Materials Protection，2019，52（4）：66-72.

[7] 程浩.轨道交通杂散电流分布特性及检测研究[D].南昌：华东交通大学，2019.

CHENG Hao. Research on Distribution Characteristics and Detection of Stray Current in Transit System[D]. Nanchang： East China Jiaotong University，2019.

[8] 王新华，陈文斌，何仁洋，等. 强制电流阴极保护管线系统的ANSYS仿真技术研究[J].腐蚀与防护，2008，29（5）： 107-110.

WANG Xinhua， CHEN Wenbin， HE Renyang， et al. Research on ANSYS simulation technology of forced current cathodic protection pipeline system[J].Corrosion & Protection， 2008，29（5）： 107-110.

[9] 周朝晖，曹阿林. 垂直分布双金属管线阴极保护交互影响分析[J].广州化工，2012，40（10）：103-105.

ZHOU Zhaohui， CAO Alin. Interaction analysis of impressed current cathode protection system for vertical pipelines[J]. Guangzhou Chemical Industry，2012，40（10）：103-105.

[10]周朝晖，王剑，曹阿林. 平行分布双金属管线阴极保护交互影响分析[J]. 河南化工，2012（6）：14-19.

ZHOU Zhaohui， WANG Jian， CAO Alin. Analysis of interaction of cathodic protection of parallel bimetallic pipelines[J]. Henan Chemical Industry，2012（6）：14-19.

[11]胡云进，钟振，方镜平. 地铁杂散电流场的有限元模拟[J].中国铁道科学，2011，32（6）：129-133.

HU Yunjin， ZHONG Zhen， FANG Jingping. Finite element simulation of subway stray current field[J]. China Railway Science，2011，32（6）：129-133.

[12]潘柳依，雷宝刚，范铮，等. ANSYS有限元法在管道阴极保护中的应用[J].材料保护，2014，47（3）：45-47.

PAN Liuyi， LEI Baogang， FAN Zheng， et al. Application of ANSYS finite element method in cathodic protection of pipelines[J]. Materials Protection， 2014，47（3）：45-47.

[13]GB/T 21448—2008， 埋地鋼制管道阴极保护技术规范[S].

[14]彭泽标.杂散电流对埋地钢质燃气管道阴极保护电位的影响研究[D]. 广州：华南理工大学，2016.

PENG Zebiao. Research on Stray Current Effect of Cathodic Protection Potential of Buried Steel Gas Pipeline[D].Guangzhou：South China University of Technology， 2016.

[15]柯甜甜，方江敏，钱瑶虹，等. 地铁杂散电流对埋地金属管道阴极保护的影响[J].城市轨道交通研究，2017（3）：90-93.

KE Tiantian， FANG Jiangmin， QIAN Yaohong， et al. Effect of metro stray current on cathode protection for buried metal pipelines[J]. Urban Mass Transit， 2017（3）：90-93.

[16]李威.地铁杂散电流腐蚀监测及防护技术[M].徐州：中国矿业大学出版社，2004.

[17]张攀峰，於孝春. 受直流杂散电流影响埋地管线的ANSYS模拟[J].腐蚀与防护，2011，32（2）：146-149.

ZHANG Panfeng， YU Xiaochun. ANSYS simulation of buried pipelines under DC stray current condition[J]. Corrosion & Protection， 2011，32（2）：146-149.

[18]肖裕生，施春华. 南京地区第四系主要地层类型及分层探讨[J].南通大学学报（自然科学版），2008，7（2）：60-65.

XIAO Yusheng， SHI Chunhua. On the division of the quaternary in the Nanjing region， eastern China[J]. Journal of Nantong University（Natural Science Edition），2008，7（2）：60-65.

[19]王果，裴潇湘. 地铁常用隧道杂散电流场三维有限元模拟[J].铁道科学与工程学报，2014，11（6）：85-91.

WANG Guo， PEI Xiaoxiang. Three-dimensional finite element simulation of different subway tunnels under stray current fields[J]. Journal of Railway Science and Engineering， 2014，11（6）：85-91.

收稿日期：2020-10-13;修回日期：2021-01-14;责任编辑：王海云

第一作者简介：田逸凡（1996—），男，河南焦作人，硕士研究生，主要从事材料腐蚀与防护方面的研究。

通讯作者：李建三副研究员。E-mail：jsLi@scut.edu.cn

田逸凡，李建三，易宏，等. 地铁轨道参数及周围环境对埋地管道保护电位影响的ANSYS分析[J].河北工业科技，2021，38（2）：77-84.

TIAN Yifan， LI Jiansan， YI Hong， et al. ANSYS analysis of the influence of subway track parameters and surrounding environment on the buried pipeline protection potential[J]. Hebei Journal of Industrial Science and Technology， 2021，38（2）：77-84.