基于迁移学习策略的压板开关状态识别

陈 翔，邹庆年，谢绍宇，陈翠琼

(广东电网有限责任公司广州供电局，广东 广州 510620)

0 引 言

随着电力系统结构日益复杂和智能电网的逐步推进，电力系统安全运维面临前所未有的挑战。在此背景下，有效提升设备运行与维护的自动巡检水平逐步成为建设重点之一[1]。压板状态、数字表读数、指针表读数等设备的识别和管理作为继保装置巡检的重要内容，其智能化和信息化水平却相对较低，难以与当前变电站智能化进程相适应，因此采用人工智能方法开展相关领域的研究，减少人为干预，有助于提升变电站运行的可靠性和安全性。

具体针对压板状态的识别，已有方法主要有图像识别方法和智能识别方法。其中大量的工作集中在图像识别领域，例如邓应松等[2]运用去噪聚类、边缘检测、布局排列分析和整体分割等图像处理算法，构建了压板状态的辨识系统；肖立军等[3]通过建立压板开关状态的标准图像数据库，基于Meanshift算法对采集的压板图像进行分割，辅以支持向量机分类器实现了压板状态的识别；许超等人[4]在研究中采用基于模型的K-means聚类学习和颜色匹配，选取最小外接矩形等特征辨识压板开关的状态；吕志宁等[5]将轮廓定位算法和仿射变换技术相结合完成压板开关的定位，而后再获取图像的Sobel边缘图像作为训练图像样本，采用SVM分类器实现压板开关状态的分类；付文龙等人[6]依据形态特征进行面积、尺寸、形状分析，对有效压板区域进行筛选，最后实现压板开关状态的识别；许根养等[7]则基于相位特征，构建基于色度畸变的改进型双边滤波器，进而基于相位竞争编码实现压板开关状态的识别。另一类方法则是基于智能学习的方法，例如卢泉等[8]基于深度学习的方法，依次通过图像采集、图像预处理、图像校正、一次整体聚类分割后，将区域图像依次送入设计好的含有3层卷积层、3层最大池化层、2层全连接层、输出为softmax的卷积神经网络，用于确定压板开关的状态；李俊达等[9]通过卷积神经网络对像素组进行卷积运算，引入修正线性单元来增加非线性模式识别，并通过特征扁平化有效实现压板的状态识别。陈海等[10]采用OpenCV颜色识别算法分割压板边缘，利用VGG神经网络模型，基于候选区域的深度学习算法，使用交叉熵损失函数和正则化计算函数的比重之和作为优化函数，完成VGG模型的训练并实现压板状态的识别。

在上述压板状态识别的方法中，传统图像识别算法的局限性在于：一方面，此类方法易受环境因素影响，例如拍照角度与距离、光线强弱等均可能造成误检；另一方面，传统图像识别算法存在特征提取以及参数设定的人工依赖问题，如果所设计的算法应用场合较多，例如若集成巡检系统不仅需要识别压板开关的状态，同时也要胜任读数表和指针表的识别，当识别对象变化时，由于某种特定图像处理算法一般不具备普适性和鲁棒性，很难扩展应用于多种不同类型的对象，因此也增加了算法设计的难度，进而影响自动巡检的识别效果。而已有的基于深度学习的算法，虽然具有通用性，但是需要大量的训练样本，考虑到压板检测是小样本电力设备目标实时检测场景，采用常规的深度学习方法面临过拟合的风险，因此也需要另寻出路。所幸的是，最近有学者在小样本数据的深度学习方向上提出了许多可行的方式[11]，例如基于深度学习网络架构的微调、深度学习与度量学习结合和深度学习与元学习结合等方法。其中，迁移学习可以有效利用轻量级、低延迟的深度学习模型，用以构建精度高、收敛速度快的学习网络[12]，因此本文选用将Inception-V3网络[13]用于资源有限和样本有限的压板状态识别的嵌入式巡检场景，有效提升模型识别的精度和速度。

1 理论基础

1.1 Inception-V3网络

Inception-V3网络是CNN发展过程中的阶段性成果，其结构如图1右侧所示[14]。它在优化网络时所采用的一个重要改进就是将n×n的大尺寸卷积层分解成为1×n和n×1这2个不对称的卷积层。该操作在增加网络深度的同时减少了参数量，又增强了网络的非线性表达能力。在该网络结构中，最后一个全连接层之前的网络层被称为瓶颈层。在本文的迁移算法中，瓶颈层的权重参数在迁移时保持不变。

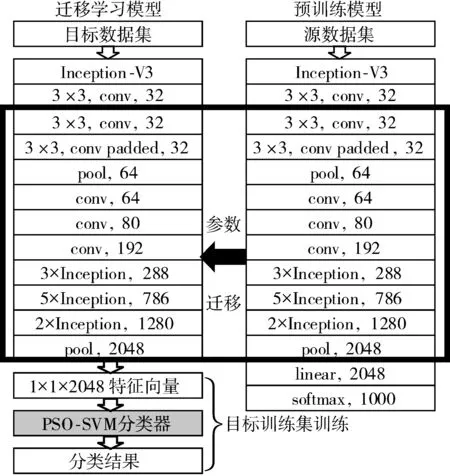
图1 本文设计的迁移学习模型

1.2 迁移学习

迁移学习的本质是利用任务、模型或数据间存在的相似性，尝试将以往“领域”的源“任务”中习得的知识迁移到新的目标任务上[15]。迁移学习的学习框架可以用领域(Domain)和任务(Task)来描述[16]，一个领域D={χ,p(X)}由特征空间χ和特征空间上的边缘分布p(X)刻画，其中X={x1,x2,…,xn}∈χ,xi∈Rd,i=1,2,…,n。对于某给定的领域D，一个任务Γ={Y,f(·)}由类标签空间Y和目标预测函数f(·)刻画，该函数可以用于预测某任意实例所属的类标签[17]。在迁移学习过程中，首先需要利用源域样本数据训练出一个可以进行识别分类的预训练模型[18]，然后在解决类似问题时，较为直接的迁移方式主要有2种：一是保持学习到的参数不变，设计不同于源网络的新的分类器；二是将学习到的参数作微调，这样可以充分利用源数据集，降低目标任务对训练样本数量的依赖。

2 压板状态识别方法

本文迁移学习的核心思想是：将ImageNet数据集上已训练好的Inception-V3模型，去掉最后面的识别层后，作为目标数据集的特征提取工具，再选择粒子群优化(Particle Swarm Optimization,PSO)算法优化的支持向量机(Support Vector Machine,SVM)分类器取代源网络的softmax分类器，实现压板状态的识别。

2.1 深度迁移神经网络的模型结构

本文采用1.2节中所述的第一种迁移方法，建立迁移学习模型结构如图1所示。图1的右侧表示基于源数据集的Inception-V3“预训练模型”，图1的左侧表示完成目标任务新建的“目标迁移学习模型”。具体算法流程如下：

1)构建源域和目标域样本集：将ImageNet数据集作为源域样本集，将巡检拍摄的压板开关照片进行处理作为目标域样本集。

2)构建预训练模型进行参数迁移：将ImageNet数据集作为预训练模型的输入，迭代训练结束后保存瓶颈层的权值和参数，将其迁移至左侧目标迁移学习模型的瓶颈层，目标迁移学习模型的瓶颈层最后输出由图像提取出的维度为1×1×2048的特征向量。

3)构建新的分类器：用PSO-SVM替换softmax分类器，该分类器的输入是步骤2中输出的特征向量。

4)目标迁移学习模型的训练和预测：用目标域训练集对目标迁移学习模型进行训练，用PSO调整SVM网络参数，而后用优化后的迁移学习模型对目标域样本验证集进行模型评估。

2.2 PSO-SVM分类器

2.2.1 SVM特征分类

SVM是一种模式分类方法，其核心思想是通过非线性映射将低维向量映射变换到一个更高维的特征空间里，使其线性可分，而后在高维空间求解最优判别函数，确定最优线性分类面[19]。假设训练样本集{(xi,yi)},xi∈Rn,yi∈{+1,-1}，定义核函数K(xi,x)=(φ(xi))Tφ(x)，则SVM的输出决策函数为：

(1)

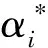
K(xi,x)=exp(-g||xi-x||2)

(2)

2.2.2 PSO算法

PSO算法是一种非线性迭代寻优方法[21]，该方法将参量为位置、速度、适应度值的粒子看作是所求问题的可能解，粒子在适应度函数的约束下自动追寻当前时刻的最优粒子，从而不断动态调整自身的速度及位移，完成全局最优解的搜索[22]，其速度和位置的更新方式如下：

(3)

(4)

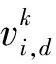
2.3 基于PSO的SVM参数优化

由式(1)与式(2)可知惩罚参数C与核函数宽度g的取值是决定SVM分类性能的关键[24]，目前用于SVM参数选择的方法主要有交叉验证法、贝叶斯方法、智能优化算法与分布估计算法等[25]。在这些算法中，PSO算法是一种全局搜索策略，其机制简单，参数少，收敛快，因此本文采用PSO算法实现SVM参数Cbest和gbest的优选，以期更准确地实现压板开关状态的预测分类。其具体流程如图2所示。

图2 PSO-SVM分类算法的流程图

3 实验设计

3.1 实验准备

实验所用的计算机为个人PC，硬件配置如下：CPU为Inter(R) Core(TM) i7-9750H，频率为2.6 GHz，内存为16 GB，显卡为Intel(R) UHD Graphics 630。操作系统为Windows 10。

在本文相关实验方案中，模型的预训练源域数据集为ImageNet，目标域数据集为在巡检现场拍摄的压板开关图片小样本数据集。其中目标域原始数据集共有60张不同角度拍摄的压板开关照片，共388个open标签样本和312个close标签样本。典型的目标数据集里的样本照片如图3所示，示例中选取了不同角度和不同光照条件的2幅训练样本图片。实验中将每张图中一行压板开关作为一个训练样本，即每幅图中相当于有5个训练样本。

图3 训练样本集图片示例

为了扩充数据规模，减少过拟合情况的发生，提高网络的泛化能力，训练中做了一定程度的数据增强。在图像处理任务中，对输入图像进行简单的缩放或者旋转，不影响图像的分类结果。因此在本文中采用如下几种操作：图像10%随机放大缩小、图像随机0～10°旋转；扩充后的目标数据集样本总数为240。由于样本量较小，故将数据集按照4∶1划分为目标域训练集和目标域测试集，即选择目标域样本中的192幅图片作为目标域训练集，其余的48幅图片作为目标域测试集。图像尺寸裁剪为224×224像素和299×299像素，适配于不同模型的图像输入。

3.2 评价标准

为全面衡量模型的分类性能，本文采用运行时间和准确率来验证算法的有效性和快速性。一方面在相同运行环境、同样的训练集和测试集的前提下，记录不同算法分类识别过程所消耗的时间，比较算法的速度；另一方面以准确率(Accuracy,Acc)作为实验的评价指标，用以验证算法的预测结果和真实结果之间的符合程度：

(5)

其中，TP、TN、FP与FN分别表示真阳性、真阴性、假阳性和假阴性。

3.3 预训练模型的构造

采用Inception-V3网络，学习率设置为0.01，Batch size设置为32，训练迭代次数设置为450，网络使用softmax分类器，以交叉熵损失函数来构造预训练模型。为了加快算法的迭代速度，经过多次实验，采用AdaGrad自适应算法[26]为各个参数设置不同的学习率，其参数更新的方式如下：

(6)

其中，学习率η=0.01，小常数ε=10-8，用于避免参数寻优初始阶段出现分母为零的情况，gi记录第i步迭代时梯度平方的值。

3.4 迁移学习模型的构造

在PSO-SVM优化算法中，设置种群数量M=20，最大迭代次数Tmax=100,c1=c2=2，对于影响粒子群收敛速度的关键参数ω，本文设计s型函数自适应调整惯性权重的动态调整函数如下：

(7)

其中，t表示当前迭代次数，ωmax=1.2,ωmin=0.8，该配置方式保证了惯性权重呈下降趋势，使得粒子在寻优过程中的迭代前期速度较快，在全局范围内具有较强的搜索能力，迭代后期则具有较强的局部收敛能力，能更精确地搜索到解。

4 结果分析

4.1 目标测试集结果分析

本文中构造的深度迁移学习模型在继承了预训练模型的参数之后，PSO-SVM的优化迭代结果如图4所示。SVM经过PSO的算法优化后，能够快速准确地得到误差指标取值最小的参数C与g，迭代寻优过程结束时的适应度约为99.53%，此时输出的最优参数值Cbest=46.09,gbest=1.86。

图4 PSO-SVM分类器参数寻优的适应度曲线

经过参数迁移和分类器设计的本文算法在目标验证集上识别结果样图如图5所示，实验迭代过程准确率和损失函数值随着迭代次数的变化曲线如图6所示。可以看到随着迭代步数的更新，识别准确率最终为99.11%，并且经过前期的参数学习，在50次迭代之后数据集的识别准确率和损失函数值已无较大波动。同时也验证了该算法的识别效果对于光照和角度并无太大依赖，均能有效识别。

图5 识别结果图

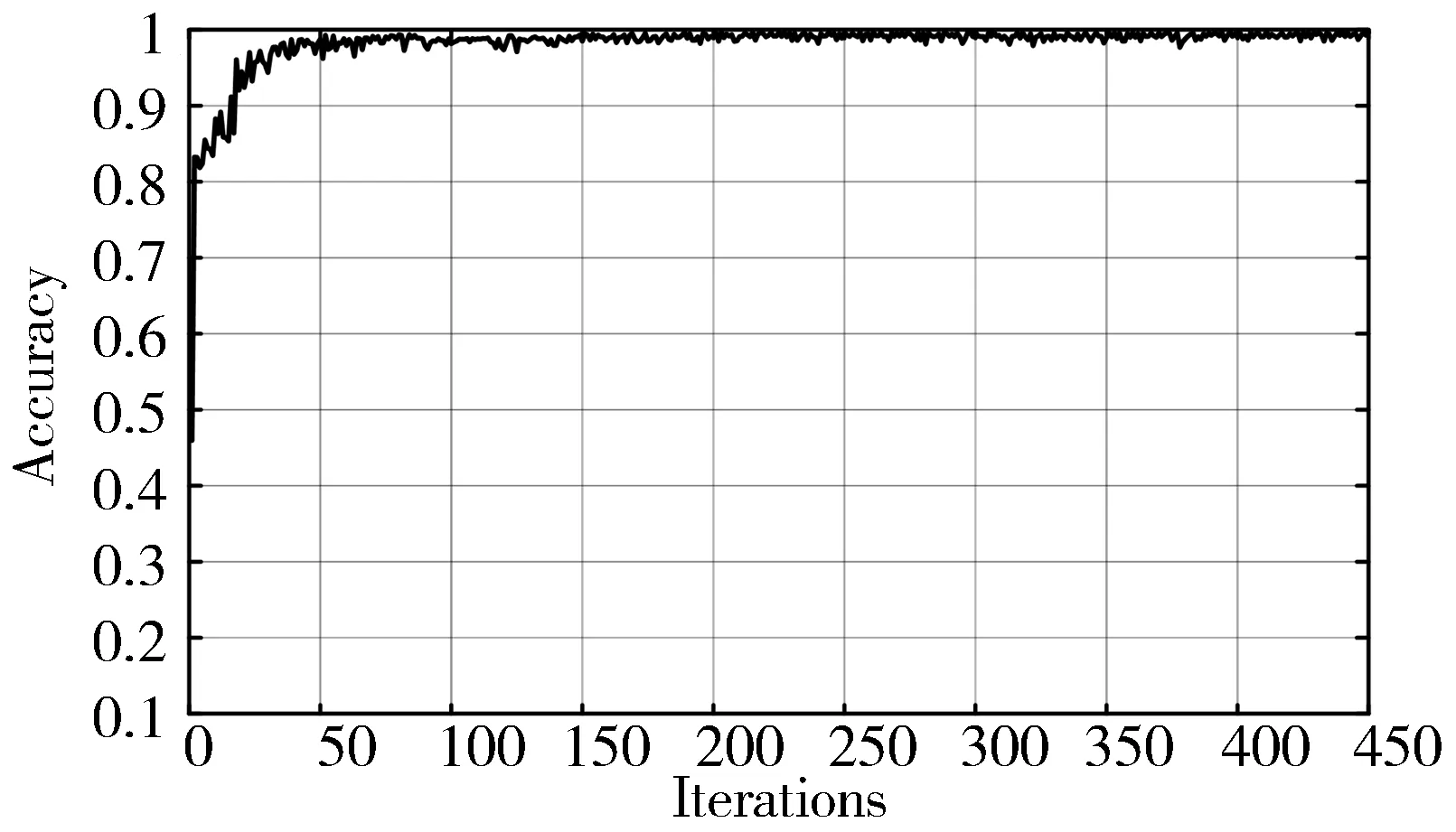
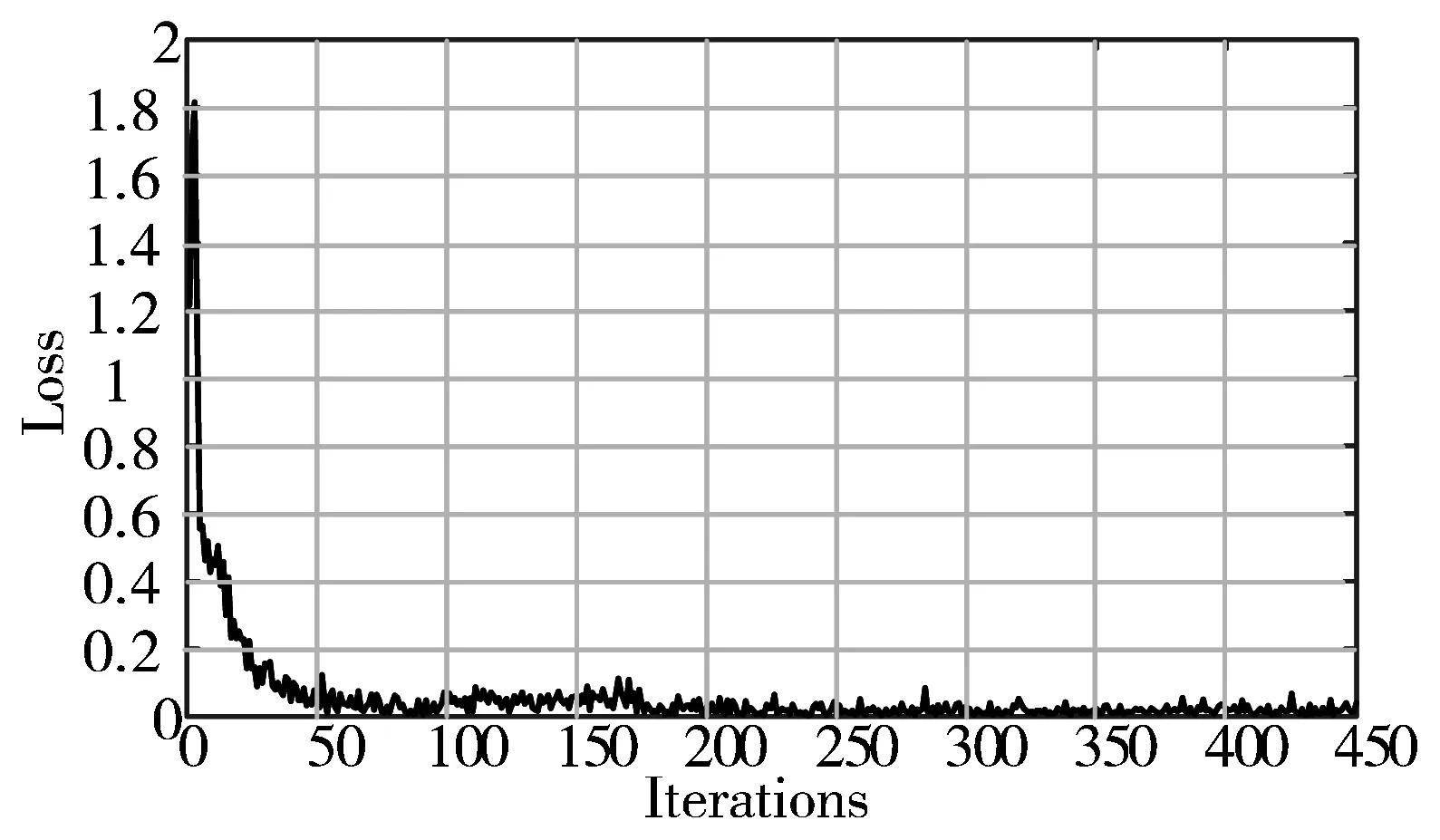
图6 本文算法在目标测试集上分类情况的实验结果

4.2 迁移学习与零基础学习的对比分析

为了验证迁移学习方式相比于随机初始化训练方式的优越性，将本文迁移算法与非迁移学习的零基础学习方式进行分析比较如图7所示，总结迁移学习对目标结果分类所带来的影响。

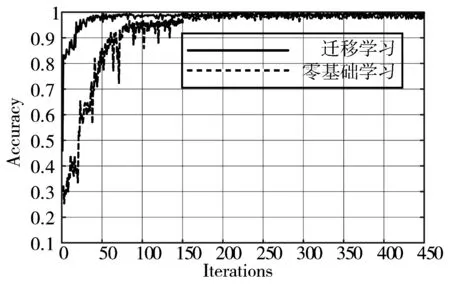
图7 迁移学习和零基础学习对目标集的分类结果对比

从图7可以看到，对目标数据集进行分类时，零基础学习的分类准确率初始值为26.3%，而迁移学习分类准确率初始值为46.2%，明显高于同期零基础学习的准确率。经过约50次迭代之后，迁移学习模式下的网络分类准确率已达98.16%，并逐步收敛趋于稳定，约190次迭代后准确率为99.61%，已接近峰值，零基础学习在第150次迭代之后才逐步趋于稳定。

经过源数据集进行训练的预训练模型，可以视为在源数据集上的一个全局最优解，因此应用于目标数据集时，更容易向新的全局最优解逼近。但是如果是随机初始值迭代，由于优化的方向是基于目前批的训练目标计算所得，因此可以视为一个局部最优解。这与全局最优解还具有差距，因此便有可能产生零基础学习时迭代曲线中的毛刺。通过对比曲线可以看出，迁移学习方式下的迭代曲线更加平滑，说明迁移学习模式可以加速深度学习神经网络的收敛速度，避免求解过程陷入局部极值。

4.3 本文算法与其他算法的对比分析

将本文算法与当前一些比较常用的深度学习模型进行对比，其中VGGNet、AlexNet和ResNet均选择mini-batch SGD优化算法，学习率均设置为0.01，Batch size均设置为32，训练迭代次数均为450。对比实验结果如表1所示。

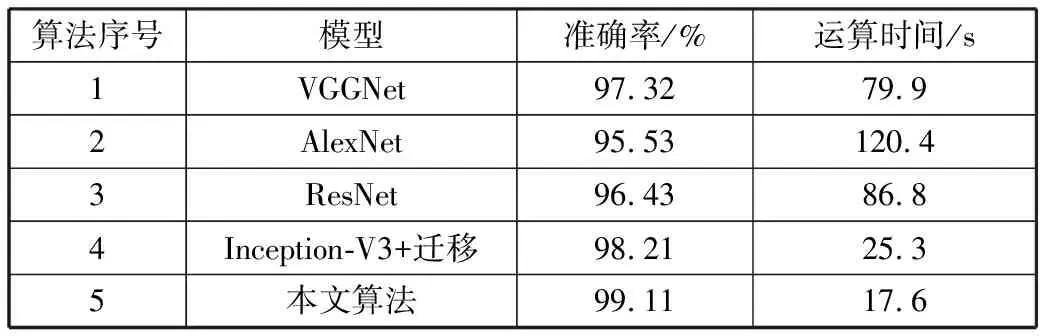
表1 本文算法与常用深度学习算法的实验结果对比

在表1中，算法1～算法3采用“零基础学习”方式，分别基于VGGNet、AlexNet和ResNet深度学习神经网络结构，直接使用目标域压板开关数据集，从头开始训练；算法4与算法5则采用迁移学习方式，基于ImageNet源数据集训练过的Inception-V3预训练模型，构造不同的分类器实现目标域数据集的分类。

从结果中可以看出，本文算法在保证精度的前提条件下运行时间明显缩短，归纳其原因如下：

1)本文场景下，迁移学习的效率优于零基础学习。

对比算法5和算法1～算法3，算法5中离线构建的预训练Inception-V3模型瓶颈层的输出在通过全连接层后已经可以有效区分源数据集ImageNet上众多类别的图像。于是可以认为该模型瓶颈层输出的节点向量可以视为任何图像的一个更加精简且表达能力更强的特征向量，这些特征即所有图像中普遍包含的形状、边缘、纹理、色度、轮廓等底层特征。所以本文通过冻结瓶颈层参数，保证其对图像基础像素特征的表达能力，然后将模型迁移到本文研究的小数据集上，设计PSO-SVM分类器，实现从底层相似特征到高维不同模式特征的聚合抽象。由于实际运行时，模型瓶颈层参数保持不变，因此只需要重新训练PSO-SVM分类器的参数，计算量大大减少，可以大幅度缩短训练时间；而使用无迁移的零基础学习的算法1～算法3需要调整网络各层的所有参数，每次迭代都需大量的卷积运算、梯度计算进行参数拟合，故处理时间较长。

2)本文场景下，PSO-SVM分类器的效率优于softmax分类器。

算法5和算法4均基于Inception-V3网络进行迁移学习，不同之处在于算法5中使用了PSO-SVM分类器取代原有的softmax分类器。SVM是根据结构风险最小化原则提出的一种针对有限样本的有监督机器学习方法，没有初始聚类中心的设置问题，在一定程度上避免了网络结构选择、过学习和欠学习等问题。同时，由于PSO算法是基于种群的并行全局搜索策略，克服了传统SVM参数选择方法中存在的数据规模受限、优化过程耗时的缺点，能快速准确地找到支持向量机的最优惩罚参数及核函数半径，从而有效进行识别，提高了算法的效率。

从分类精度的角度考虑，由于经过ImageNet大数据训练过的Inception-V3网络瓶颈层固定参数部分相当于一个具备先验知识的普适图像特征提取器，所提取的图像底层特征具有较强的泛化能力，能很好地适应同类型但数据不同的图像分类识别任务，解决了零基础深度学习缺乏大量训练数据而导致的过拟合问题，有效提高了网络识别的精度。

实际上，康奈尔大学的Yosinski等人[27]对深度学习神经网络的可迁移性进行了较全面的试验，并在其论文中给出了对之后的深度学习和迁移学习均具有重要指导意义的结论：1)深度学习的底层网络提取的是具有通用性的基础特征，适合进行迁移；2)网络结构的迁移有利于网络学习和优化效率的提升。本文结论也为该论述提供了一个相关实例佐证。

4.4 迭代次数与识别精度之间的关系

为了进一步探讨算法的实用性，给出迁移学习模型的测试精度和运行时间与迭代次数的关系如表2所示。

表2 迭代次数与识别精度之间的关系

在本文前述研究中采用的迭代次数为450次，主要是呈现分类精度的变化趋势。结合图6和表2数据可见，算法分类准确率前期随着迭代次数增加呈增加的趋势，但当训练的迭代次数达到150次之后，模型的识别精度已进入收敛阶段，此时分类准确率已达到98.56%，而后随着迭代次数的增加，其分类准确率均在99.05%附近有微量波动。由此可知，在实际应用场景中，为了达到快速性和准确度之间的折衷，可以设置迭代次数为200次～250次，此时的运行时间只需约8～10 s。因此，在迭代次数相对较少的情况下，本文算法也能得到较高的准确率，并且识别的准确率都高于传统深度学习模型。因此，本文算法是可行及高效的。

综上所述，本文算法在目标数据集上运行时间远低于VGGNet、AlexNet和ResNet等模型的前提下保证了分类准确率，表明了算法的有效性和优越性，同时说明利用参数迁移和轻量级卷积神经网络相结合的策略，可以在保证识别精度的前提条件下快速收敛，因此适用于对实时性和硬件有严格要求的电力设备巡检场景。

5 结束语

针对智能变电站中电力设备数据集样本较少以及电力设备巡检存在的准确性和实时性的问题，本文提出了基于较轻量级Inception-V3网络的改进目标检测算法，采用迁移学习的方式，提高了小样本条件下压板开关状态图像识别的匹配度和运行效率。实验运行说明将本文所述方法与移动巡检终端相结合，可缓解人工巡检时可能产生的误操作问题，为变电站智能化管理提供有效的技术支持。